python经典百题之反向输出数字
题目:输入一个整数,并将其反转后输出。
程序分析
我们需要对输入的整数进行反转,即将整数的数字反向排列。
方法1:使用字符串反转
解题思路
- 将整数转换为字符串,然后对字符串进行反转。
代码实现
def reverse_integer_using_string(num):# Convert the integer to a string, reverse it, and convert it back to an integerreversed_num = int(str(num)[::-1])return reversed_num# Example usage
num = 12345
reversed_num = reverse_integer_using_string(num)
print(f"The reversed integer of {num} is: {reversed_num}")
优缺点
- 优点:
- 简单,易于理解和实现。
- 缺点:
- 需要进行整数到字符串的转换,空间复杂度较高。
方法2:数学运算反转整数
解题思路
- 使用数学运算进行整数反转。
代码实现
def reverse_integer_using_math(num):reversed_num = 0while num != 0:remainder = num % 10reversed_num = reversed_num * 10 + remaindernum //= 10return reversed_num# Example usage
num = 12345
reversed_num = reverse_integer_using_math(num)
print(f"The reversed integer of {num} is: {reversed_num}")
优缺点
- 优点:
- 不需要额外空间,空间复杂度为O(1)。
- 缺点:
- 需要进行数学运算,可能溢出。
方法3:使用字符串拼接反转整数
解题思路
- 将整数转换为字符串,逐个字符反向拼接成新字符串,然后将新字符串转换为整数。
代码实现
def reverse_integer_using_string_concatenation(num):if num < 0:return int(str(num)[0] + str(num)[:0:-1])else:return int(str(num)[::-1])# Example usage
num = 12345
reversed_num = reverse_integer_using_string_concatenation(num)
print(f"The reversed integer of {num} is: {reversed_num}")
优缺点
- 优点:
- 不需要额外空间,空间复杂度为O(1)。
- 缺点:
- 需要进行整数到字符串的转换,可能稍微慢一些。
总结和推荐
- 推荐方法2(数学运算反转整数):
- 简单,不需要额外空间,适用于大多数情况。
综上所述,推荐使用方法2来反转整数。
相关文章:

python经典百题之反向输出数字
题目:输入一个整数,并将其反转后输出。 程序分析 我们需要对输入的整数进行反转,即将整数的数字反向排列。 方法1:使用字符串反转 解题思路 将整数转换为字符串,然后对字符串进行反转。 代码实现 def reverse_integer_usin…...

复习Day08:哈希表part01:242.有效的字母异位词、349. 两个数组的交集、1. 两数之和、160. 相交链表
之前的blog:https://blog.csdn.net/weixin_43303286/article/details/131765317 我用的方法是在leetcode再过一遍例题,明显会的就复制粘贴,之前没写出来就重写,然后从拓展题目中找题目来写。辅以Labuladong的文章看。然后刷题不用…...
用 Pytest+Allure 生成漂亮的 HTML 图形化测试报告
本篇文章将介绍如何使用开源的测试报告生成框架 Allure 生成规范、格式统一、美观的测试报告。 通过这篇文章的介绍,你将能够: 将 Allure 与 Pytest 测试框架相结合; 如何定制化测试报告内容 执行测试之后,生成 Allure 格式的测…...

Python字符串索引解码乱码谜题
输入数行“数字字母”字符组成的乱码字符串,根据谜题规则解码出乱码字符串中隐藏的单词信息。 (本笔记适合熟悉python字符串索引操作的 coder 翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.python.org/ Free:大咖免费“圣经”…...

协议栈——收发数据(拼接网络包,自动重发,滑动窗口机制)
目录 协议栈何时发送数据~ 数据长度 IP模块的分片功能 发送频率 网络包序号~利用syn拼接网络包ack确认网络包完整 确定偏移量 服务器ack确定收到数据总长度 序号作用 双端告知各自序号 协议栈自动重发机制 大致流程 ack等待时间如何调整 是…...

传输层协议——TCP、UDP
目录 1、UDP 协议(用户数据报协议) 协议特点 报文首部格式 2、TCP 协议(传输控制协议) 协议特点 报文首部格式 TCP连接建立时的三次握手 TCP拆除连接的四次挥手 TCP的流量控制 TCP的拥塞控制 3、传输层端口号 三类端口…...

优化您的Spring应用程序:缓存注解的精要指南
优化您的Spring应用程序:缓存注解的精要指南 前言详细说明1. Cacheable:2. CacheEvict:3. CachePut:4. Caching:5. CacheConfig: 项目中的实现前提使用 前言 当我们构建和运行Spring应用程序时,…...

Java之原子性问题的解决
2. 原子性 2.1 volatile-问题 代码分析 : package com.itheima.myvolatile; public class Demo {public static void main(String[] args) {MyThread1 t1 new MyThread1();t1.setName("小路同学");t1.start(); MyThread2 t2 new MyThread2();t2.setName(&q…...
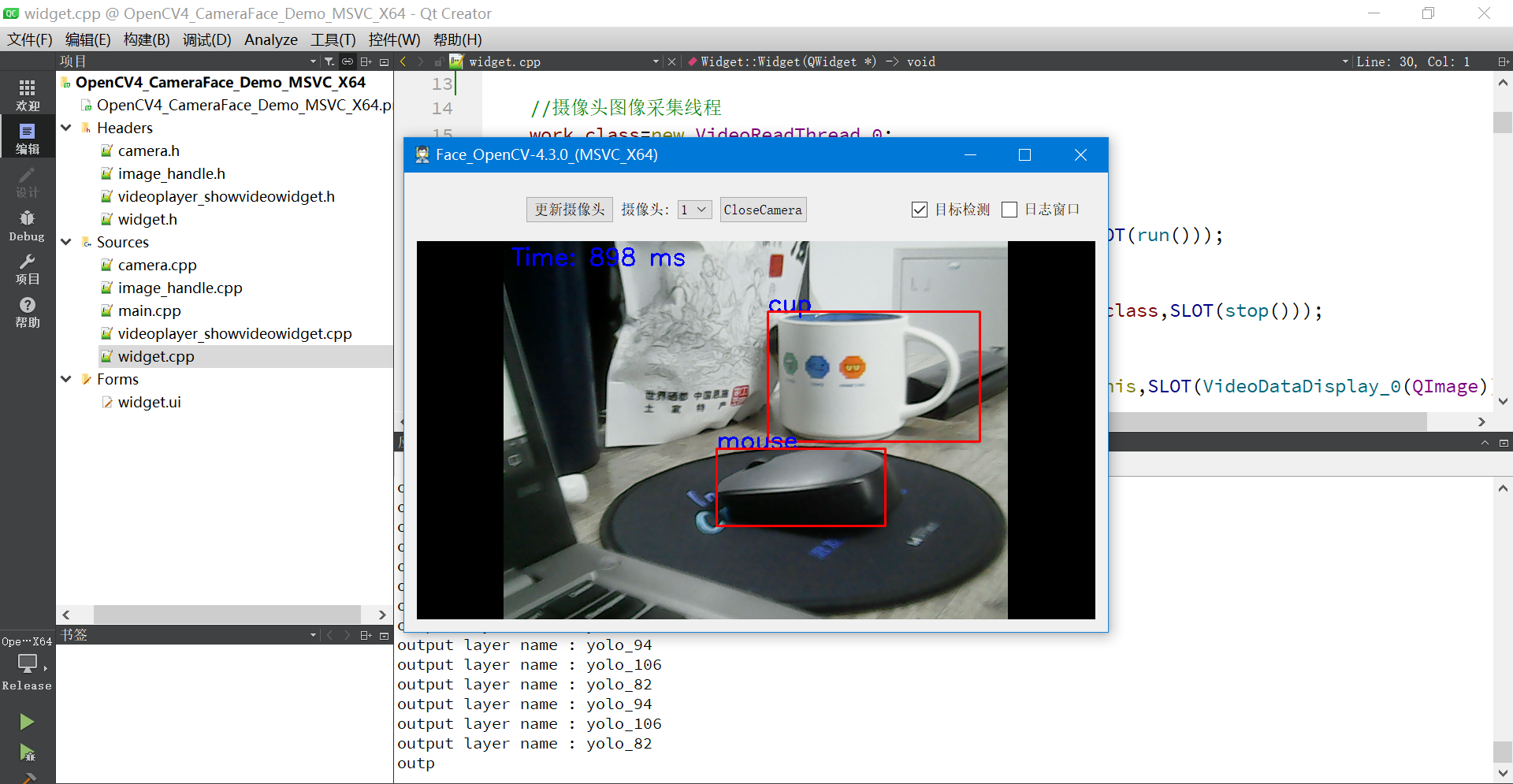
实时目标检测:基于YOLOv3和OpenCV的摄像头应用
一、前言 随着人工智能和计算机视觉技术的不断发展,目标检测成为了智能监控、自动驾驶、机器人等领域的关键技术之一。实时目标检测更是对系统的反应速度和准确度提出了更高的要求。本文介绍使用OpenCV和YOLOv3实现实时目标检测的方法,演示如何使用OpenCV调用YOLOv3模型进行…...

【软考】4.2 关系代数
《 关系代数 》 表和表之间的逻辑运算 笛卡尔积:S1 x S2 投影:π;选择某一列(属性);一个关系R的投影操作结果也是一个关系,记作Πa,它由从关系R中选出的A列元素构成;选择…...
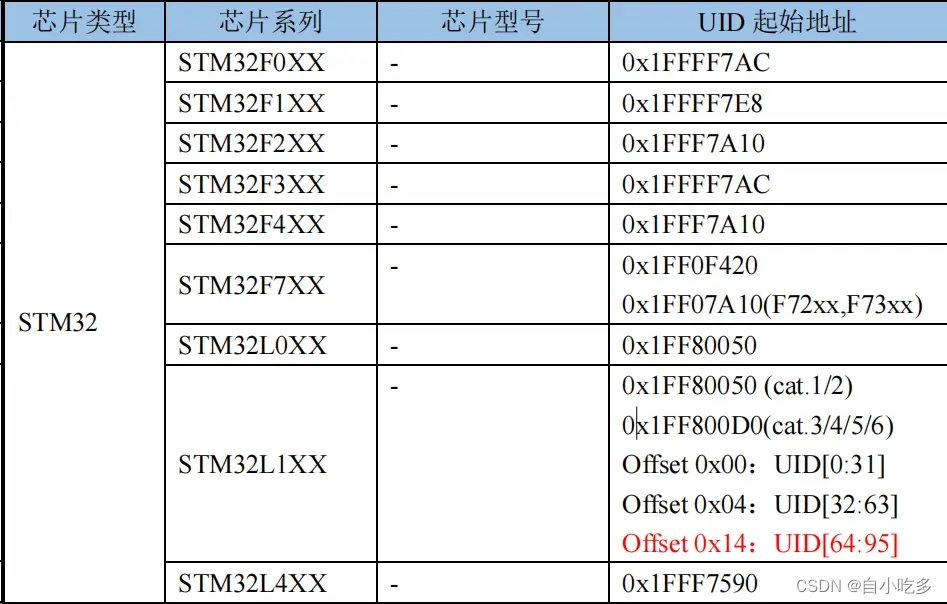
STM32F4学习笔记读取芯片UID和MAC地址
一、简介 在嵌入式设备开发过程中有时会需要为设备设置唯一的ID用以标识设备唯一,比如要求同一总线上的所有设备ID不能重复,要求设备具体唯一的MAC地址等等。每个STM32微控制器都自带一个96位的唯一ID,这个ID在任何情况下都是唯一且不允许修…...

webpack优化策略
这三点是webpack优化策略的一部分,具体解释如下: 优化正则匹配(Test):在webpack的配置中,test属性是一个正则表达式,用于匹配需要应用该loader的文件的扩展名。在您提供的代码中,te…...
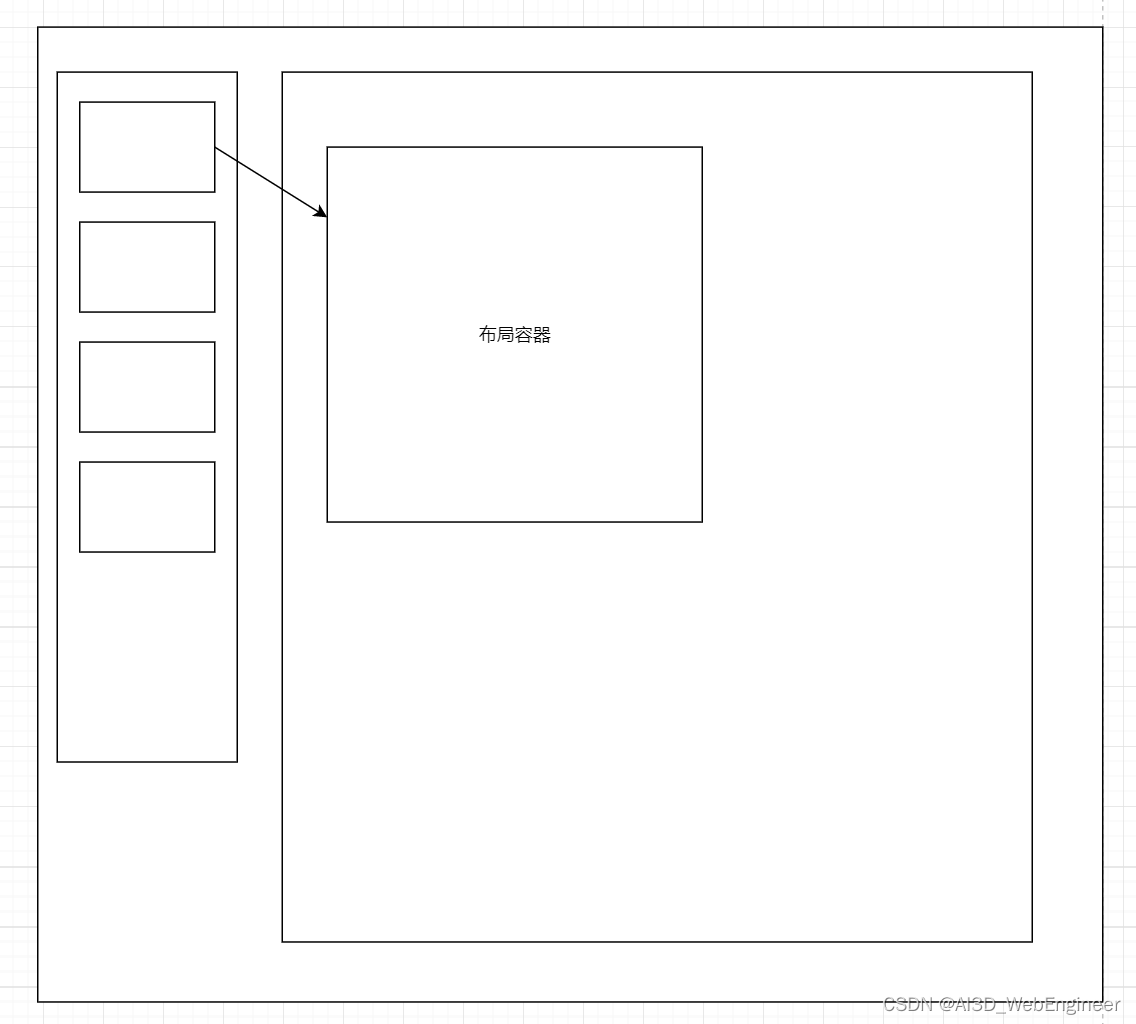
讲讲项目里的仪表盘编辑器(三)布局组件
布局容器处理 看完前面两章的讲解,我们对仪表盘系统有了一个大概的理解。接着我们讲讲更深入的应用。 上文讲解的编辑器只是局限于平铺的组件集。而在编辑器中,还会有一种组件是布局容器。它允许其他组件拖拽进入在里面形成自己的一套布局。典型的有分页…...

Linux- 后台运行符、nohup、disown
& &在Unix-like的操作系统(如Linux和macOS)的shell中,特别是在Bash这样的shell中,经常用作后台运行符号。让我们深入了解一下其功能和用法。 &作为后台运行符号: 基本用法: 当我们在一个命令或者一组命令…...

开发过程教学——交友小程序
交友小程序 1. 我的基本信息2. 我的人脉2.1 我的关注2.2 我的粉丝 3. 我的视频4. 我的相册 特别注意:由于小程序分包限制2M以内,所以要注意图片和视频的处理。 1. 我的基本信息 数据库表: 我的基本信息我的登录退出记录我的登录状态&#x…...

正则表达式 Regular Expression学习
该文章内容为以下视频的学习笔记: 10分钟快速掌握正则表达式_哔哩哔哩_bilibili正则表达式在线测试工具:https://regex101.com/, 视频播放量 441829、弹幕量 1076、点赞数 19330、投硬币枚数 13662、收藏人数 26242、转发人数 2768, 视频作者 奇乐编程学…...
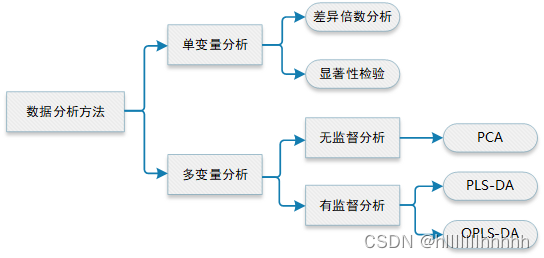
代谢组学最常用到的数据分析方法(五)
代谢组学是一门对某一生物或细胞所有低分子质量代谢产物(以相对分子质量<1000的有机和无机的代谢物为研究核心区)进行分析的新兴学科。因此从复杂的代谢组学数据中确定与所研究的现象有关的代谢物,筛选出候选生物标记物成为代谢物组学研究…...

105.从前序与中序遍历序列构造二叉树
力扣题目链接(opens new window) 根据一棵树的前序遍历与中序遍历构造二叉树。 注意: 你可以假设树中没有重复的元素。 例如,给出 前序遍历 preorder [3,9,20,15,7] 中序遍历 inorder [9,3,15,20,7] 返回如下的二叉树: class Solution { public:Tr…...
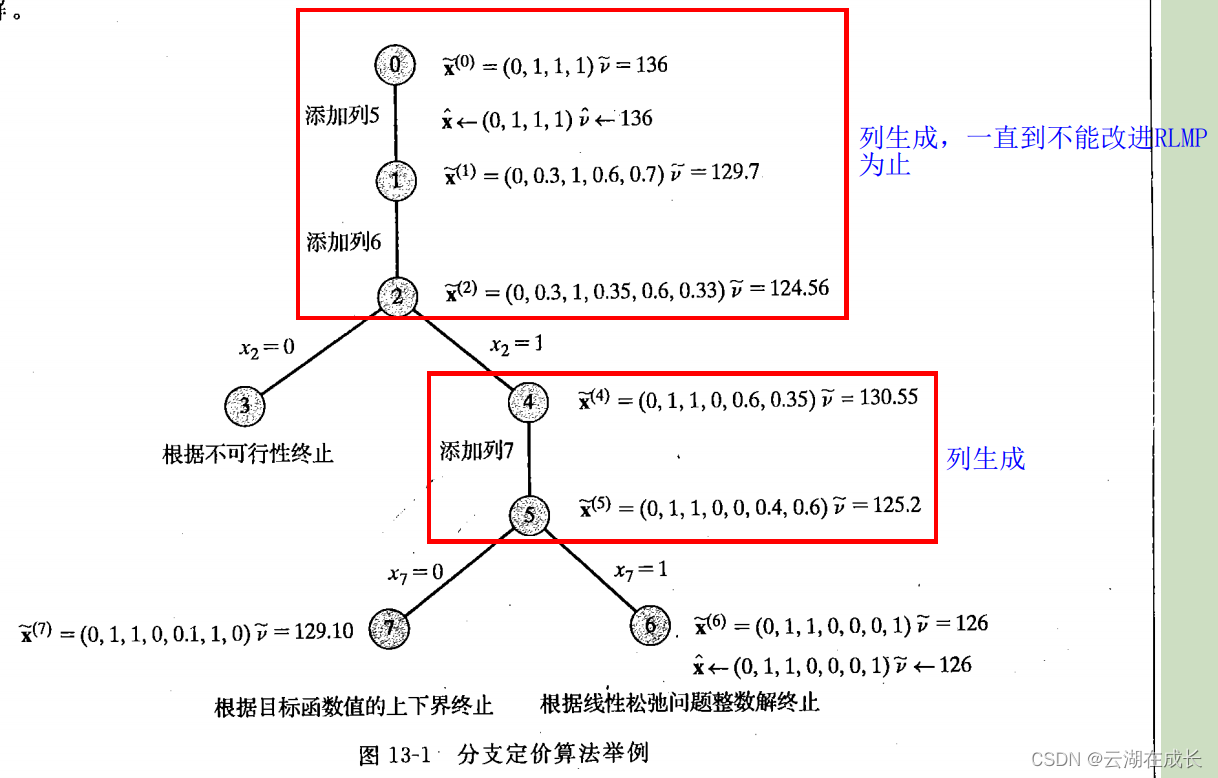
分支定界、分支切割、分支定价的区别
目录 1.从原理的角度 (1)分支定界: (2)分支切割: (3)分支定价: 2.从分支树的角度 (1)分支定界 (2)分支切割 &…...
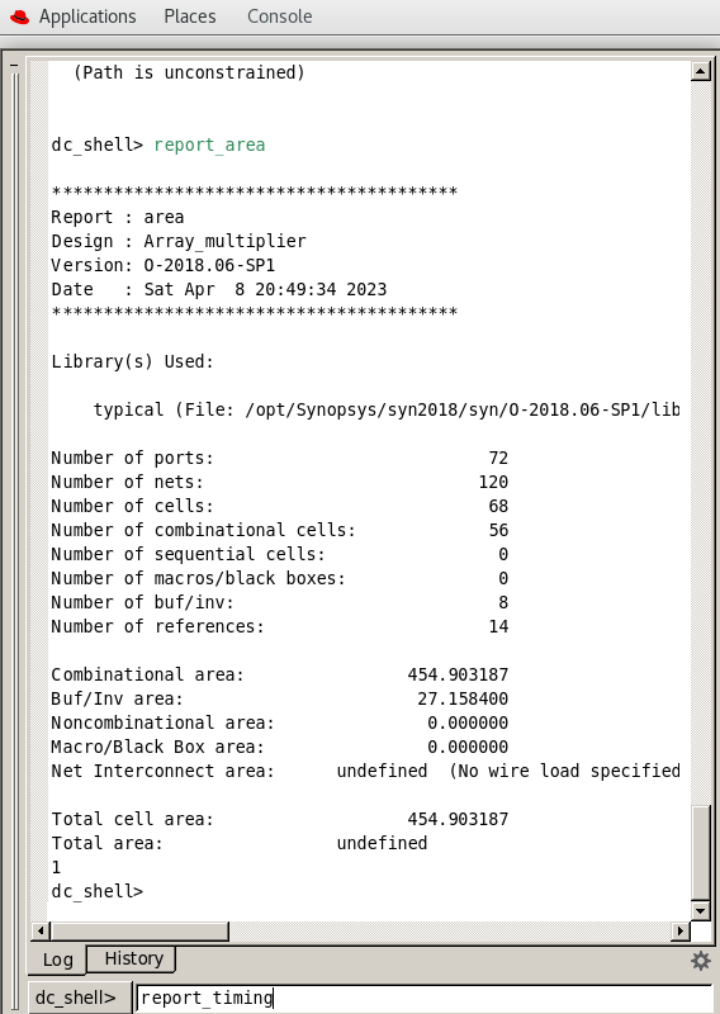
数字IC前端学习笔记:数字乘法器的优化设计(阵列乘法器)
相关阅读 数字IC前端https://blog.csdn.net/weixin_45791458/category_12173698.html?spm1001.2014.3001.5482 数字信号处理作为微处理器的核心部件,是决定着总体处理器性能的因素之一,而数字乘法器是最常见的一种数字信号处理电路。通常情况下&#…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
