堆优化迪氏最短单源路径原理及C++实现
时间复杂度
O(ElogE),E是边数。适用与稀疏图。
使用前提
边的权为正。可以非连通,非连通的距离为-1。
原理
优选队列(小根堆)记录两个数据:当前点到源点距离,当前点。先处理距离小的点;如果距离相等,先处理谁都可以。可以用pair记录,不用重写小于。优先队列只记录如下情况的距离:
一,{0,源点}。
二,任意点的最短距离和可以直达的边。
如果是有向图,则入队数量等于边数,计算出起点最短路径的那一轮。无向图,则翻倍。显然出队数量等于入队数量。优先队列入队和出队时间复杂度都是O(logn),故总时间复杂度为O(nlogn)。
样例
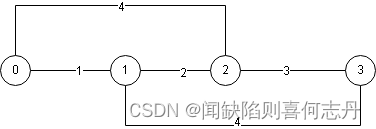
下表分析源点为0的处理过程。
| 初始 | 入队{0,0} | |
| 出队{0,0} | 入队{1,1} | 0到源点的最短距离为0 |
| 入队{4,2} | ||
| 出队{1,1} | 入队{2,0} | |
| 入队{3,2} | 1到源点的最短距离为1 | |
| 入队{5,3} | ||
| 出队{2,0} | 0已经处理 | |
| 出队{3,2} | 入队{7,0} | 2到源点最短距离为3 |
| 入队{5,1} | ||
| 入队{6,3} | ||
| 出队{4,2} | 2已经处理 | |
| 出队{5,1} | 1已经处理 | |
| 出队{5,3} | … 3到源点的最短距离是5。 | |
| … | ||
核心代码
非常的简洁。
typedef pair<long long, int> PAIRLLI;
class CHeapDis
{
public:
CHeapDis(int n)
{
m_vDis.assign(n, -1);
}
void Cal( int start, const vector<vector<pair<int, int>>>& vNeiB)
{
std::priority_queue<PAIRLLI, vector<PAIRLLI>, greater<PAIRLLI>> minHeap;
minHeap.emplace(0, start);
while (minHeap.size())
{
const long long llDist = minHeap.top().first;
const int iCur = minHeap.top().second;
minHeap.pop();
if (-1 != m_vDis[iCur])
{
continue;
}
m_vDis[iCur] = llDist;
for (const auto& it : vNeiB[iCur])
{
minHeap.emplace(llDist + it.second, it.first);
}
}
}
vector<long long> m_vDis;
};
测试用例
#include <iostream>
#include <vector>
#include <queue>
#include <assert.h>
using namespace std;
class CDebugDis : public CHeapDis
{
public:
using CHeapDis::CHeapDis;
void Assert(const vector<int>& vDis)
{
for (int i = 0; i < vDis.size(); i++)
{
assert(vDis[i] == m_vDis[i]);
}
}
};
struct CDebugParam
{
int n;
vector<vector<std::pair<int, int>>> edges;
int s;
vector<int> dis;//答案
};
int main()
{
vector<CDebugParam> params = { {1,{{}},0,{0}},
{2,{{}},0,{0,-1}},{2,{{{1,2}},{{0,2}}},0,{0,2} }
,{3,{{{1,4},{2,5}},{{0,4}},{{0,5}}},0,{0,4,5} }
,{3,{{{1,4},{2,8}},{{0,4},{2,3}},{{0,8},{1,3}}},0,{0,4,7} }
,{3,{{{1,4},{2,8}},{{0,4},{2,5}},{{0,8},{1,5}}},0,{0,4,8} }
,{4,{{{1,1},{2,4}},{{0,1},{2,2},{3,4}},{{0,4},{1,2},{3,3}},{{1,4},{2,3}}},0,{0,1,3,5}}
};
for (const auto& par : params)
{
CDebugDis n2Dis(par.n);
n2Dis.Cal(par.s, par.edges);
n2Dis.Assert(par.dis);
}
}
测试环境
win7 VS2019 C++17
相关下载
源码及测试用例:
https://download.csdn.net/download/he_zhidan/88390995
doc版文档,排版好
https://download.csdn.net/download/he_zhidan/88348653
相关文章:

堆优化迪氏最短单源路径原理及C++实现
时间复杂度 O(ElogE),E是边数。适用与稀疏图。 使用前提 边的权为正。可以非连通,非连通的距离为-1。 原理 优选队列(小根堆)记录两个数据:当前点到源点距离,当前点。先处理距离小的点;如果…...

Leetcode202. 快乐数
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 编写一个算法来判断一个数 n 是不是快乐数。 「快乐数」 定义为: 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为 1࿰…...

【MySQL】MySql常见面试题总结
目录 一、什么是sql注入 二、sql语句的执行流程 三、内连接和外连接的区别 四、Union和Union All 有什么区别 五、MySql如何取差集 六、DELETE和TRUNCATE有什么区别 七、count(*)和count(1)的区别 八、MyISAM和InnoDB的区…...

【Java 进阶篇】JDBC PreparedStatement 详解
在Java中,与关系型数据库进行交互是非常常见的任务之一。JDBC(Java Database Connectivity)是Java平台的一个标准API,用于连接和操作各种关系型数据库。其中,PreparedStatement 是 JDBC 中一个重要的接口,用…...

嵌入式Linux应用开发-驱动大全-第一章同步与互斥①
嵌入式Linux应用开发-驱动大全-第一章同步与互斥① 第一章 同步与互斥①1.1 内联汇编1.1.1 C语言实现加法1.1.2 使用汇编函数实现加法1.1.3 内联汇编语法1.1.4 编写内联汇编实现加法1.1.5 earlyclobber的例子 1.2 同步与互斥的失败例子1.2.1 失败例子11.2.2 失败例子21.2.3 失败…...
【计算机网络】 基于UDP的简单通讯(客户端)
文章目录 客户端流程代码实现添加头文件以及库依赖加载库创建套接字发送接收数据关闭套接字、卸载库 测试 客户端 流程 客户端跟服务端差不多,也要先加载库,在加载库之后也要创建套接字,但是客户端一定是没有绑定ip地址的,之后是…...
【云备份项目】:环境搭建(g++、json库、bundle库、httplib库)
文章目录 1. g 升级到 7.3 版本2. 安装 jsoncpp 库3. 下载 bundle 数据压缩库4. 下载 httplib 库从 Win 传输文件到 Linux解压缩 1. g 升级到 7.3 版本 🔗链接跳转 2. 安装 jsoncpp 库 🔗链接跳转 3. 下载 bundle 数据压缩库 安装 git 工具 sudo yum…...
电脑右键新建记事本不见了--设置恢复篇(无需操作注册表)
电脑右键新建记事本不见了–设置恢复篇(无需修改注册表) 电脑不知怎么想右键新建记事本结果竟然不见了,搜寻网上的都是什么修改注册表,粘贴代码修复(感觉太复杂了),这里介绍通过设置内重新对记…...
- 序列生成器)
JavaScript内置对象 - Array数组(四)- 序列生成器
序列生成器是生成一个指定起始值和结束值的序列,并且根据指定间隔长度,生成序列数组。 完成此功能需要使用到Array内置对象的from()对象,以及类数组相关知识,前面几篇有相关案例进行演示。 地址一:JavaScript内置对象…...
GD32F103x IIC通信
1. IIC通信 1.IIC的介绍 IIC总线有两条串行线,其一是时钟线SCK(同步),其二是数据线SDA。只有一条数据线属于半双工。应用中,单片机常常作为主机,外围器件可以挂载多个。(当然主机也可以有多个。…...

什么是FOSS
FOSS 是指 自由和开放源码软件(Free and Open Source Software)。这并不意味着软件是免费的。它意味着软件的源代码是开放的,任何人都可以自由使用、研究和修改代码。这个原则允许人们像一个社区一样为软件的开发和改进做出贡献。...
C++语言GDAL批量裁剪多波段栅格图像:基于像元个数裁剪
本文介绍基于C 语言的GDAL模块,按照给定的像元行数与列数,批量裁剪大量多波段栅格遥感影像文件,并将所得到的裁剪后新的多波段遥感影像文件保存在指定路径中的方法。 在之前的文章中,我们多次介绍了在不同平台,或基于不…...

简单丝的tab切换栏(html/CSS)
#html <!DOCTYPE html> <html lang"en" > <head><meta charset"UTF-8"><title>CSS实现左右滑动选项卡效果</title><link rel"stylesheet" href"https://cdnjs.cloudflare.com/ajax/libs/meyer-res…...
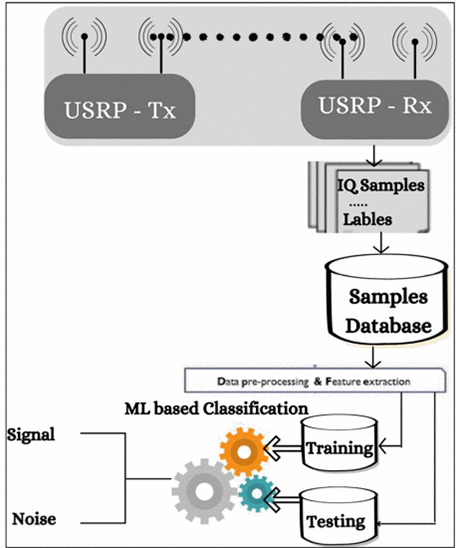
LabVIEW开发带式谱感测技术
LabVIEW开发带式谱感测技术 如今,通过无线网络传输的数据量正在迅速增加,并导致频谱稀缺。超过数十亿的无线设备将被连接起来,并需要互联网接入。因此,无线电频谱管理方案的效率不足以授予对所有设备的访问权限。在频谱分配中&am…...
认识柔性数组
在C99中,结构中的最后一个元素允许是未知大小的数组,这就叫做柔性数组成员 限制条件是: 结构体中最后一个成员未知大小的数组 1.柔性数组的形式 那么我们怎样写一个柔性数组呢 typedef struct st_type {int i;int a[0];//柔性数组成员 }ty…...
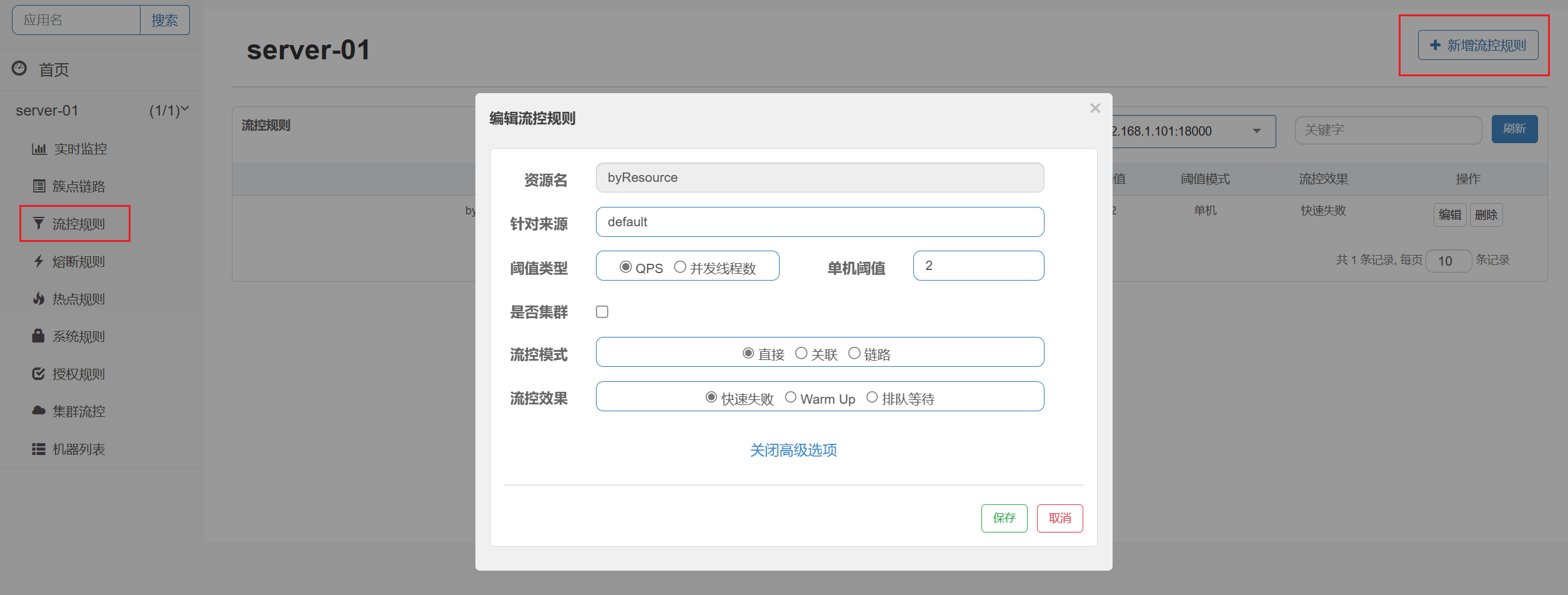
熔断、限流、降级 —— SpringCloud Alibaba Sentinel
Sentinel 简介 Sentinel 是阿里中间件团队开源的,面向分布式服务架构的高可用流量防护组件,主要以流量为切入点,从限流、流量整形、熔断降级、系统负载保护、热点防护等多个维度来帮助开发者保障微服务的稳定性 Sentinel 提供了两个服务组件…...

python经典百题之反向输出数字
题目:输入一个整数,并将其反转后输出。 程序分析 我们需要对输入的整数进行反转,即将整数的数字反向排列。 方法1:使用字符串反转 解题思路 将整数转换为字符串,然后对字符串进行反转。 代码实现 def reverse_integer_usin…...

复习Day08:哈希表part01:242.有效的字母异位词、349. 两个数组的交集、1. 两数之和、160. 相交链表
之前的blog:https://blog.csdn.net/weixin_43303286/article/details/131765317 我用的方法是在leetcode再过一遍例题,明显会的就复制粘贴,之前没写出来就重写,然后从拓展题目中找题目来写。辅以Labuladong的文章看。然后刷题不用…...
用 Pytest+Allure 生成漂亮的 HTML 图形化测试报告
本篇文章将介绍如何使用开源的测试报告生成框架 Allure 生成规范、格式统一、美观的测试报告。 通过这篇文章的介绍,你将能够: 将 Allure 与 Pytest 测试框架相结合; 如何定制化测试报告内容 执行测试之后,生成 Allure 格式的测…...

Python字符串索引解码乱码谜题
输入数行“数字字母”字符组成的乱码字符串,根据谜题规则解码出乱码字符串中隐藏的单词信息。 (本笔记适合熟悉python字符串索引操作的 coder 翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.python.org/ Free:大咖免费“圣经”…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...
