java - 七大比较排序 - 详解
前言
本篇介绍了七大比较排序,直接插入排序,希尔排序,冒泡排序,堆排序,选择排序,快速排序,归并排序,一些简单思想+代码实现,如有错误,请在评论区指正,让我们一起交流,共同进步!
文章目录
- 前言
- 1. 直接插入排序
- 2. 希尔排序
- 3. 冒泡排序
- 4. 堆排序 - 基于完全二叉树
- 5. 选择排序
- 6 快速排序:
- 6.2 非递归快排
- 7. 归并排序
- 总结
本文开始
1. 直接插入排序
思路 : 一组数据, 当插入下标为i时的数据, 比较前面i-1个数据, 如果前面i-1个数据中,有数据大于插入为i位置下标的数据, i-1位置数据, 向后移动, 直至i-1个数据中没有小于i下标的值, 再将i下标的值插入j+1位置;
时间复杂度: O(N^2)
空间复杂度: O(1)
稳定性: 稳定
直接插入代码实现:
public static void insertSort(int[] array) {//默认第一个有序不用排序, 从第二个开始排序for (int i = 1; i < array.length; i++) {int tmp = array[i];//作为判断标准,作为插入元素int j = i-1; //循环完,还需要使用到j下标, 所以拿出来定义for (; j >= 0; j--) {//判断tmp 是否 大于下标为j的元素if(array[j] > tmp) {//小于就前移一位array[ j+1] = array[ j ];}else {//插入值大于插入值前面的元素. 直接跳出//array[ j+1 ] = tmp;break;}}//比较完后,需要将插入值放到j+1位置array[j+1] = tmp;}}
2. 希尔排序
思想: 希尔排序, 直接插入排序的优化版本; 每组分组, 组数任意,这再进行排序(插入排序); 这里可以将数据除2依次分组;
数据分组不一定是相邻的,假设10个元素分5组,每组两个元素,在5位置的元素组数减5就是0位置,就是跟5一组的另一个元素;
以上可得到, 一个位置加减组数,可以得到一组的另外元素位置
平均时间复杂度: O(n^1.3)
空间复杂度: O(1)
希尔排序代码实现:
public static void shellSort(int[] array) {int gap = array.length;//初始化组数, 每个元素为一组,在除2分组while (gap > 1) {//shell排序shell(array,gap);//分组gap /= 2;}//第一次gap越界没有排, 此时以整体为一组,进行排序shell(array,gap);}public static void shell(int[] array,int gap) {//gap => 分几组的组数// 从第gap个开始排序for (int i = gap; i < array.length; i++) {int tmp = array[i];//作为判断标准,作为插入元素int j = i-gap; //循环完,还需要使用到j下标, 所以拿出来定义for (; j >= 0; j--) {//判断tmp 是否 大于下标为j的元素if(array[j] > tmp) {//小于就前移gap位array[j+gap] = array[j];}else {//插入值大于插入值前面的元素. 直接跳出break;}}//比较完后,需要将插入值放到j+1位置array[j+gap] = tmp;}}
3. 冒泡排序
思路: 升序为例,遍历数组, 比较两个相邻的值, 如果左位置大于右位置,就交换两个的位置, 一直比较数组结束;
时间复杂度: O(n^2)
空间复杂度: O(1)
稳定性: 稳定
冒泡排序优化实现 :
定义一个标志,某趟排序标志没有改变, 证明数组已经有序,不需要继续排序了,直接跳出即可;
发现每趟冒泡排序都会确定一个位置, 让每趟排序少1次比较;
public static void bubbleSort(int[] array) {//arrat.length个元素, 跑arrat.length-1趟//定义一个标志,某趟排序,标志没有改变, 证明数组已经有序,不需要继续排序了,直接跳出即可boolean flag = false; for (int i = 0; i < array.length - 1; i++) {for (int j = 0; j < array.length - 1 - i; j++) {if(array[j] > array[j+1]) {//交换swap(array,j,j+1);flag = true;}}if(flag == false) {break;}}}
4. 堆排序 - 基于完全二叉树
思路: 创建一个堆, 以大根堆为例, 要获取升序数组,只知道堆顶是最大,不知道左右孩子谁大, 需要堆排;
将堆顶与尾元素交换, 再向下调整为大根堆, 使尾元素下标-1, 循环执行此过程直至尾元素减为0;
时间复杂度: O(n*logn)
空间复杂度: O(logn)
稳定性: 不稳定
堆排序代码实现:
public static void heapSort(int[] array) {//堆排先有堆,建立一个大根堆creatHeap(array);//大根堆的左右不能确定谁大谁小,所以需要堆排int end = array.length-1;while (end > 0) {//首尾元素交换swap(array,0,end);//此时保持大根堆,需要重新向下调整shiftDown(array,0,end);//排好最后一个位置, 最后一个位置有序,数组减1排下一个,第二大的就可以放到倒数第二,依次类推直到end结束//最后层序遍历,可以获取升序数组end--;}}//建堆(基于完全二叉树): 从最后一颗子树开始,使用向下调整(父节点位置向下移动到子节点位置)private static void creatHeap(int[] array) {//父节点下标 = ( 孩子节点下标 - 1 ) / 2for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) {shiftDown(array,parent,array.length);}}//向下调整需要获取子节点位置, 所以给了父节点, 根据二叉树规则得到子节点下标,// 得到子节点下标,需要保证它不越界,// 通过观察每个子节点最大都不会超过数组长度, 所以给一个通用的数组长度即可private static void shiftDown(int[] array, int parent, int end) {//确定孩子节点int child = 2 * parent + 1;//必须有左孩子,保证孩子节点不越界while (child < end) {//左右孩子谁大,右孩子大则更新右孩子节点下标,否则不更新if(child + 1 < end && array[child] < array[child + 1]) {child++;//下标+1表示到了右孩子下标}//比较父子节点大小if(array[child] > array[parent]) {swap(array,child,parent);//更新父子节点位置,向下进行调整的,父子节点都是向下的parent = child;child = 2 * parent + 1;}else {break;//孩子小于父亲这棵树就不用换}}}
5. 选择排序
**思路①: 遍历数组, 第一个 i 位置有序,从i+1位置开始到数组结束(待排序位置), 寻找最小值下标, 提前定义变量记录最小值下标位置, 最小值不是一次就可以找到的, 可能需要不断更新需要记录; 找到之后交换最小值位置与 i 位置元素, 之后一次i++,重复上述操作即可;
思路②:
定义两个下标left, right表示每次遍历的范围,使用 i 遍历数组(数组范围[left+1,right]);
循环找最大最小值下标maxIndex,minIndex,当left < right 时,找到两个下标, 分别进行交换(交换最小值与left位置,最大值与right交换);
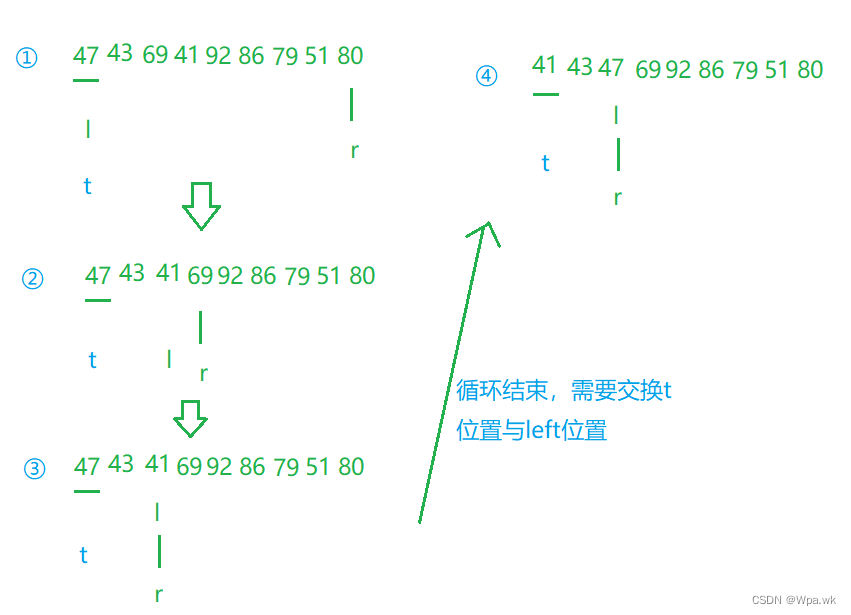
特殊情况:交换最小值与左下标, 交换后会遇到特殊情况最大值刚好位于left位置, 交换最小值后,最大值正好跑到最小值位置, 此时需要更新最大值位置; **
特殊情况如图: left位置与maxIndex位置一致时产生的问题
时间复杂度: O(n^2)
空间复杂度: O(1)
稳定性: 不稳定
选择排序代码1实现:
public static void selectSort(int[] array) {//遍历数组for (int i = 0; i < array.length; i++) {int minIndex = i;//在剩余待排序序列中找到最小的, 如果找不到直接下一个for (int j = i + 1; j < array.length; j++) {if(array[j] < array[minIndex]) {//更改最小值下标minIndex = j;}}//找到最小值与起始位置交换, 每次i位置就为起始位置, 在剩余length-i位置中找比i位置小的元素,找到交换//直到数组找完 i > lengthint tmp = array[i];array[i] = array[minIndex];array[minIndex] = tmp;}}
选择排序代码2实现:
public static void selectSort2(int[] array) {int left = 0;int right = array.length - 1;while (left < right) {//定义两个存储下标int minIndex = left;int maxIndex = left;//从待排序序列中找, 第一个认为有序, 找到最大最小值位置for (int i = left + 1; i < array.length; i++) {if(array[i] < array[minIndex]) {minIndex = i;}if(array[i] > array[maxIndex]) {maxIndex = i;}}//交换, 最小值换到左边, 最大值换到右边swap(array,left,minIndex);//存在特殊情况最大值刚好位于left位置, 交换最小值后,最大值正好跑到最小值位置// 此时需要更新最大值位置if(maxIndex == left) {maxIndex = minIndex;}//在交换最大值位置swap(array,right,maxIndex);left++;right--;}}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}
6 快速排序:
思路: 快排递归是一样的,只是使用的找基准值下标的方法不同;
①挖坑法找基准值下标思路: 每次以第一个为基准定义为tmp(left位置), 先从数组右边开始找到大于tmp的数就将它放入left位置, 再从左边找到小于tmp的数,将他放到right位置, 直到left == right相遇时, tmp再放到left位置, 此时它的位置就是基准值位置;
② hoare法: 先记录最左边下标位置t, 循环结束后还需要交换t位置与新的left位置;
以第一个为基准值, 先从右边找到比基准值小的下标, 从左边找到比基准值大的下标, 再交换二者元素,依次交换直至left > right 循环结束;
好的情况:
时间复杂度: O(n*logn)
空间复杂度: O(logn)
坏蛋情况:
时间复杂度: O(n^2)
空间复杂度: O(n)
稳定性: 不稳定
快排代码: 基准值左边全部小于基准值, 基准值右边全部大于基准值,
patition方法能返回基准值下标, 再返还基准值下标前,代码已经完成排序操作了;
public void quickSort(int[] array) {quick(array,0,array.length-1);}private void quick(int[] array, int start, int end) {//判断越界if(start >= end) {return;}//基准值: 它的左边小于基准值,右边大于基准值;//获取下一次基准值下标,依次为界,将数组分为两个子序列//左右两边重复次过程int index = patition(array,start,end);//左右两边快排quick(array,start,index - 1);quick(array,index + 1,end);}//挖坑法 -private int patition(int[] array, int left, int right) {//获取第一个为基准值,一个数组的最左边int tmp = array[left];//遍历数组while (left < right) {//先遍历右边找到比基准值小的//从最右边往左边找, 如果都是小于第一个的值, 会越界需要判断while (left < right && array[right] > tmp) {right--;}//找到小的就放到左边array[left] = array[right];while (left < right && array[left] < tmp) {left++;}//左边找到大的就放到右边array[right] = array[left];}array[left] = tmp;//左右相遇时,此下标就是下一次分割数组的位置return left;}
**快排方法2:
private int patition2(int[] array, int left, int right) {//获取第一个为基准值,一个数组的最左边int tmp = array[left];int t = left;//遍历数组while (left < right) {//先遍历右边找到比基准值小的//从最右边往左边找, 如果都是小于第一个的值, 会越界需要判断 => 逆序情况while (left < right && array[right] > tmp) {right--;}//从最左边往右边找, 如果都是大于第一个的值, 会越界需要判断 => 升序情况while (left < right && array[left] < tmp) {left++;}//交换左右下标值swap(array,left,right);}swap(array,t,left);//左右相遇时,此下标就是下一次分割数组的位置return left;}
hoare法模拟图示
交换全过程
快排代码优化:
优化1: 三数取中法, 在数组最左边,中间,最右边,比较获取中间的值下标, 与数组第一个元素交换;
patition每次会返回基准值下标, 为了让基准值在数组中间,均分数组
基准值分割数组,不一定是均等分割,这样排序速度就会减慢
优化2:减少递归次数, 排序到最后会趋向大部分有序, 对于大部分有序直接插入排序是最快的
//优化2:if(end - start + 1 < 10) {insertSort(array,start,end);return;}//优化1: 尽量让基准值为于每次数组中间,均分数组能加快排序速度int midTree = minTree(array,start,end);//在最左边,中间,最右边,获取中间的值下标, 与数组第一个元素交换swap(array,midTree,start);
插入排序:
private void insertSort(int[] array, int start, int end) {for (int i = start + 1; i <= end; i++) {//从第二个开始,记录此时值int tmp = array[i];int j = i-1;for (; j >= start ; j--) {//数组中值大于 tmp j位置值前移1if(array[j] > tmp) {array[j+1] = array[j];}else {//前面的已经排行序了, 如果小于tmp直接跳出就行,不要看前面的了break;}}array[j] = tmp;}}
6.2 非递归快排
非递归思想:
第一次数组前后下标已知(0,array.length-1),从第二次开始使用栈;
求的基准值下标,根据基准值分割数组获取子数组;
判断获得的子数组元素是否大于1,大于1才让数组或子数组左右下标,放入栈中; 栈不为空,弹出栈中元素,进行快排patition方法(跟递归方法中的patition一样,这里就不写了)直到栈中元素为空
public void quickSort2(int[] array) {//Deque实现的顺序栈Deque<Integer> stack = new ArrayDeque<>();//获取数组的前后下标int left = 0;int right = array.length - 1;//找基准值int pivot = patition(array,left,right);//保证基准值左边至少有一位数if(pivot > left + 1) {stack.push(left);stack.push(pivot - 1);}//保证基准值右边至少有1个元素if(pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}while (!stack.isEmpty()) {//先弹出右下标,再弹出左下标right = stack.pop();left = stack.pop();pivot = patition(array,left,right);//求新的基准值下标//保证基准值左边至少有一位数if(pivot > left + 1) {stack.push(left);stack.push(pivot - 1);}//保证基准值右边至少有1个元素if(pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}}//跳出循环, 再也没有子数组时,快排完毕;}
7. 归并排序
7.1 归并排序递归实现:
归并思想:
分治法: 先分,使用递归,将数组分为最小单位1, 再合并看自己要求,这里按升序为例, 合并两个数组,需定义一个新数组,数组1与数组2比较大小, 谁小谁先放入新数组, 可能两数组长度不一样, 长的数组的剩余元素直接放入新数组即可, 最后再将新数组组放到旧数组即可;
归并时间复杂度: O(n*logn)
空间复杂度: O(n)
稳定性: 稳定
归并排序实现代码:
public void mergeSort(int[] array) {mergeSortChild(array,0,array.length-1);}public void mergeSortChild(int[] array,int left,int right) {//防止越界,需要判断//当left == right: 说明递归结束if(left >= right) {return;}//找到中间下标,从而拆分数组int mid = (left + right) / 2;//拆分左边mergeSortChild(array,left,mid);//拆分右边mergeSortChild(array,mid + 1,right);//合并merge(array,left,right,mid);}//升序为例public void merge(int[] array, int left, int right, int mid) {//比较数组,需要遍历下标int s1 = left;int s2 = mid + 1;//数组2的开始下标//创建一个新数组,存放排好序的数组int[] tmp = new int[right - left + 1];int k = 0;//记录新数组元素个数//数组1与数组2都有元素进行比较while (s1 <= mid && s2 <= right) {//因为是升序,谁小谁先进新数组tmpif(array[s1] < array[s2]) {tmp[k++] = array[s1++];}else {tmp[k++] = tmp[s2++];}}//如果比较的s1,s2数组不等长(两数组中元素个数不一致)//再次遍历剩余数组,将剩余元素放入新数组中while (s1 <= mid) {tmp[k++] = array[s1++];}while (s2 <= right) {tmp[k++] = array[s2++];}//新数组在放到旧数组中for (int i = 0; i < tmp.length; i++) {array[i + left] = array[i];}}
归并排序非递归实现:
思想: 分组排序,一组一个一个,在一组两个两个,再四个四个, 分完一组再归并;
代码实现:
public void mergeSort2(int[] array) {//定义组数int gap = 1;while (gap < array.length) {for (int i = 0; i < array.length; i += gap*2) {//i += gap*2 => 排完一组排一组,使最左下标更换以至于遍历全部数组元素int left = i;int mid = left + gap - 1;//中间下标越界if(mid > array.length) {mid = array.length - 1;}//右下标越界int right = mid + gap;if(right > array.length) {right = array.length - 1;}//排序merge(array,left,right,mid);}//增加每组的个数1->2,2->4等等gap *= 2;}}
总结
✨✨✨各位读友,本篇分享到内容如果对你有帮助给个👍赞鼓励一下吧!!
感谢每一位一起走到这的伙伴,我们可以一起交流进步!!!一起加油吧!!!
相关文章:

java - 七大比较排序 - 详解
前言 本篇介绍了七大比较排序,直接插入排序,希尔排序,冒泡排序,堆排序,选择排序,快速排序,归并排序,一些简单思想代码实现,如有错误,请在评论区指正…...

项目集成七牛云存储sdk
以PHP为例 第一步:下载sdk PHP SDK_SDK 下载_对象存储 - 七牛开发者中心 sdk下载成功之后,将sdk放入项目中,目录选择以自己项目实际情况而定。 注意:在examples目录中有各种上传文件的参考示例,这里我们主要参考的是…...

docker-compose一键启动neo4j
下载镜像 docker pull neo4j:3.5.22-community 编写配置文件 参考文档 编写docker-compose.yml文件 version: "3"services:neo4j:image: neo4j:3.5.22-communitycontainer_name: neo4j restart: alwaysports:- 7474:7474- 7687:7687environment:- NEO4J_AUTH:ne…...

深入剖析@ConfigurationProperties注解
当我们构建Spring Boot应用程序时,配置属性通常是不可或缺的一部分。Spring Boot提供了多种方式来管理这些属性,其中之一是使用ConfigurationProperties注解。这篇博客将详细解释ConfigurationProperties注解以及如何使用它来管理和映射配置属性。 什么…...
北京开发APP需要多少钱
北京开发一个移动应用(APP)的费用因多种因素而异,包括项目的规模、复杂性、所需功能、设计要求、技术选择、开发团队的经验和地理位置等。一般来说,北京的APP开发费用通常较高,因为这是中国的主要技术和创新中心之一&a…...
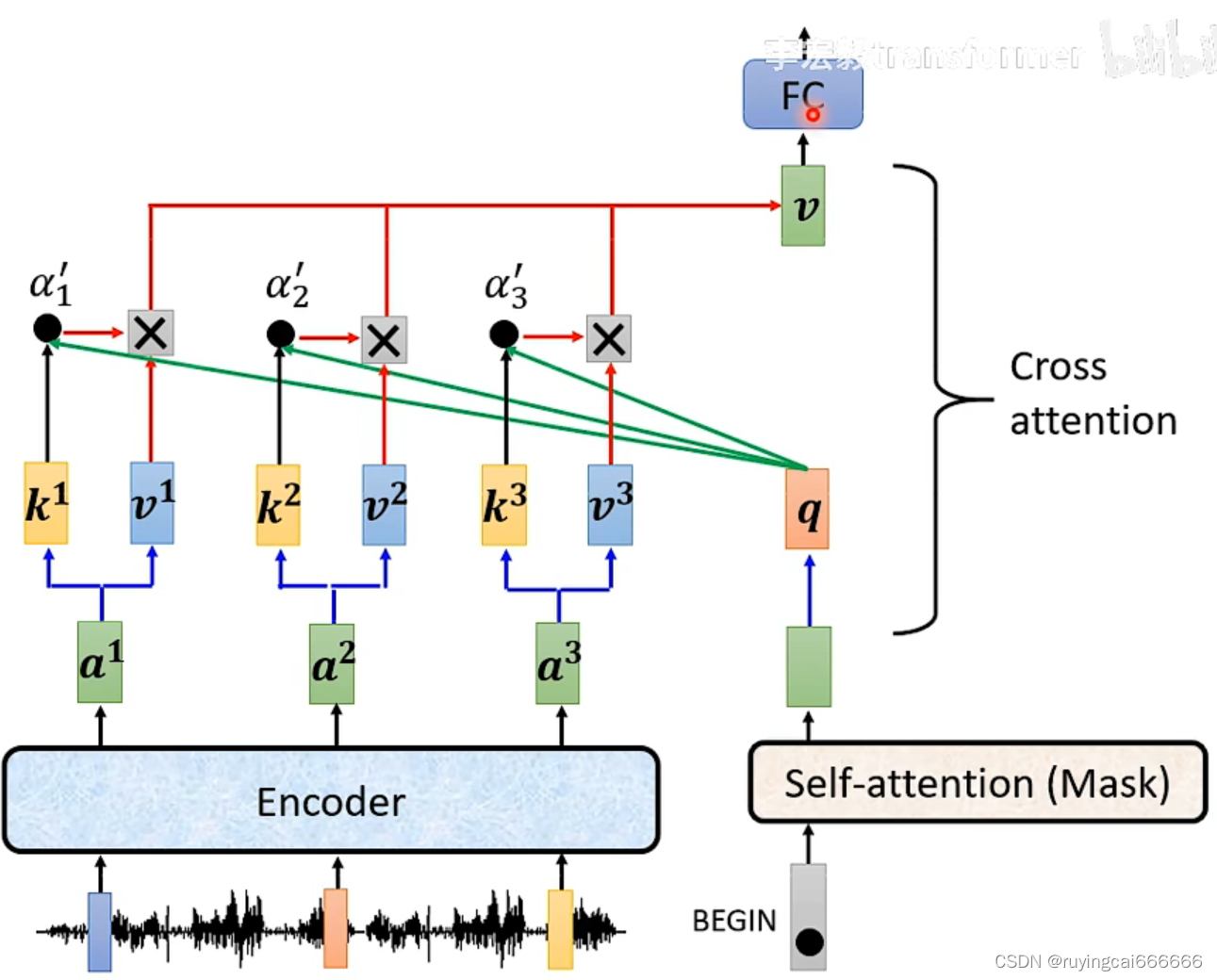
self-attention、transformer、bert理解
参考李宏毅老师的视频 https://www.bilibili.com/video/BV1LP411b7zS?p2&spm_id_frompageDriver&vd_sourcec67a2725ac3ca01c38eb3916d221e708 一个输入,一个输出,未考虑输入之间的关系!!! self-attention…...

junit @ExcludePackages排除多个包
在JUnit中,可以使用ExcludePackages注解来排除多个包。该注解可以用在测试类或测试方法上。 如果要排除多个包,可以在ExcludePackages注解的value属性中使用数组来指定要排除的包名。例如,要排除包com.example.package1和com.example.packag…...
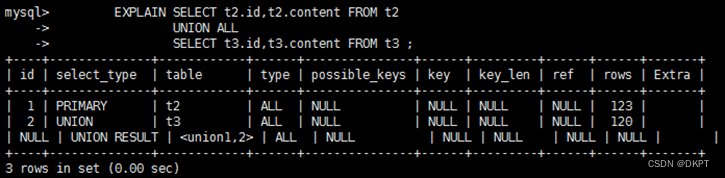
Explain执行计划字段解释说明---select_type、table、patitions字段说明
1、select_type的类型有哪些 2、select_type的查询类型说明 1、SIMPLE 简单的 select 查询,查询中不包含子查询或者UNION 2、PRIMARY 查询中若包含任何复杂的子部分,最外层查询则被标记为Primary 3、DERIVED 在FROM列表中包含的子查询被标记为DERIVED(衍生)&…...
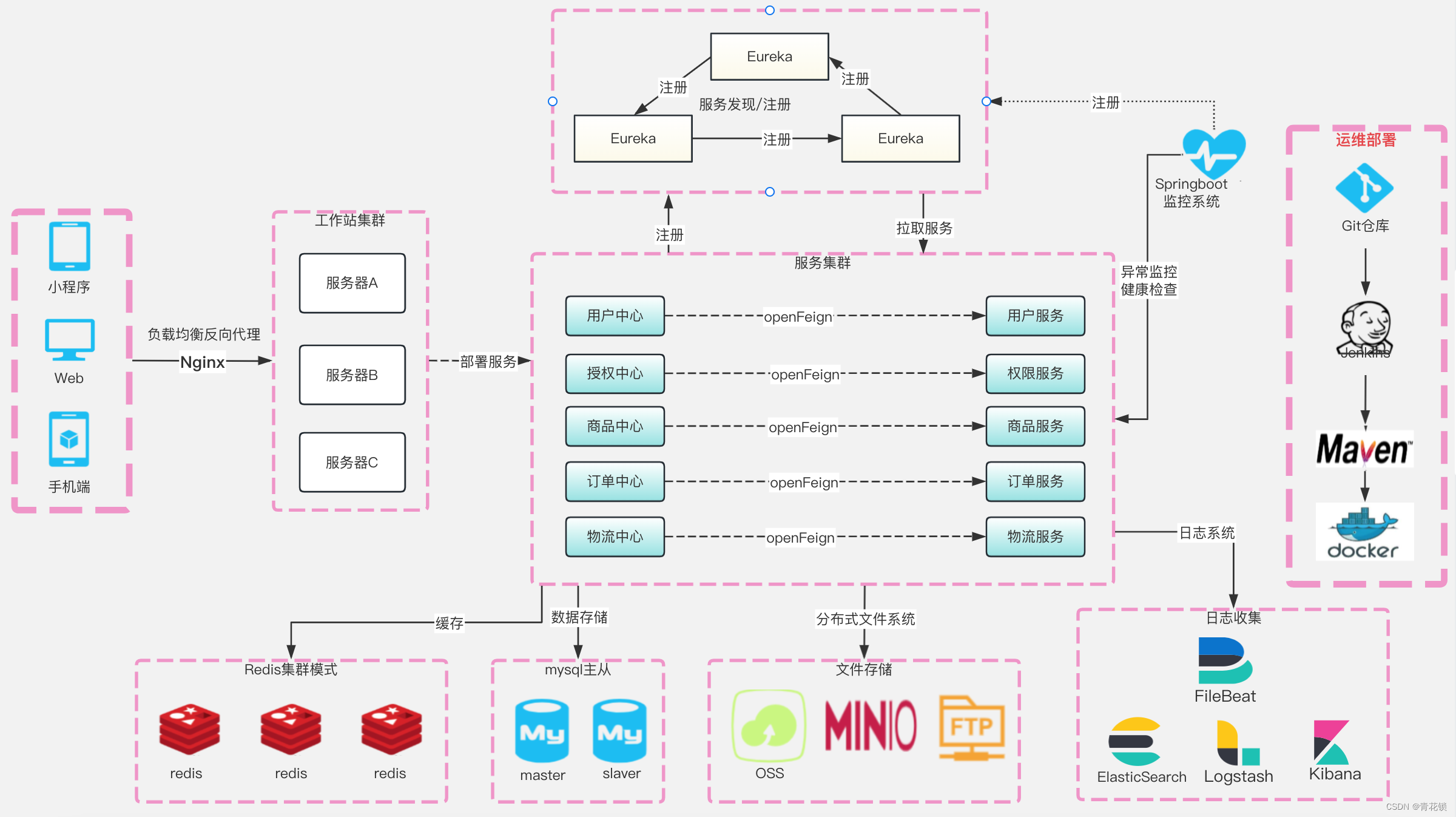
云原生微服务 第六章 Spring Cloud Netflix Eureka集成远程调用、负载均衡组件OpenFeign
系列文章目录 第一章 Java线程池技术应用 第二章 CountDownLatch和Semaphone的应用 第三章 Spring Cloud 简介 第四章 Spring Cloud Netflix 之 Eureka 第五章 Spring Cloud Netflix 之 Ribbon 第六章 Spring Cloud 之 OpenFeign 文章目录 系列文章目录前言1、OpenFeign的实现…...
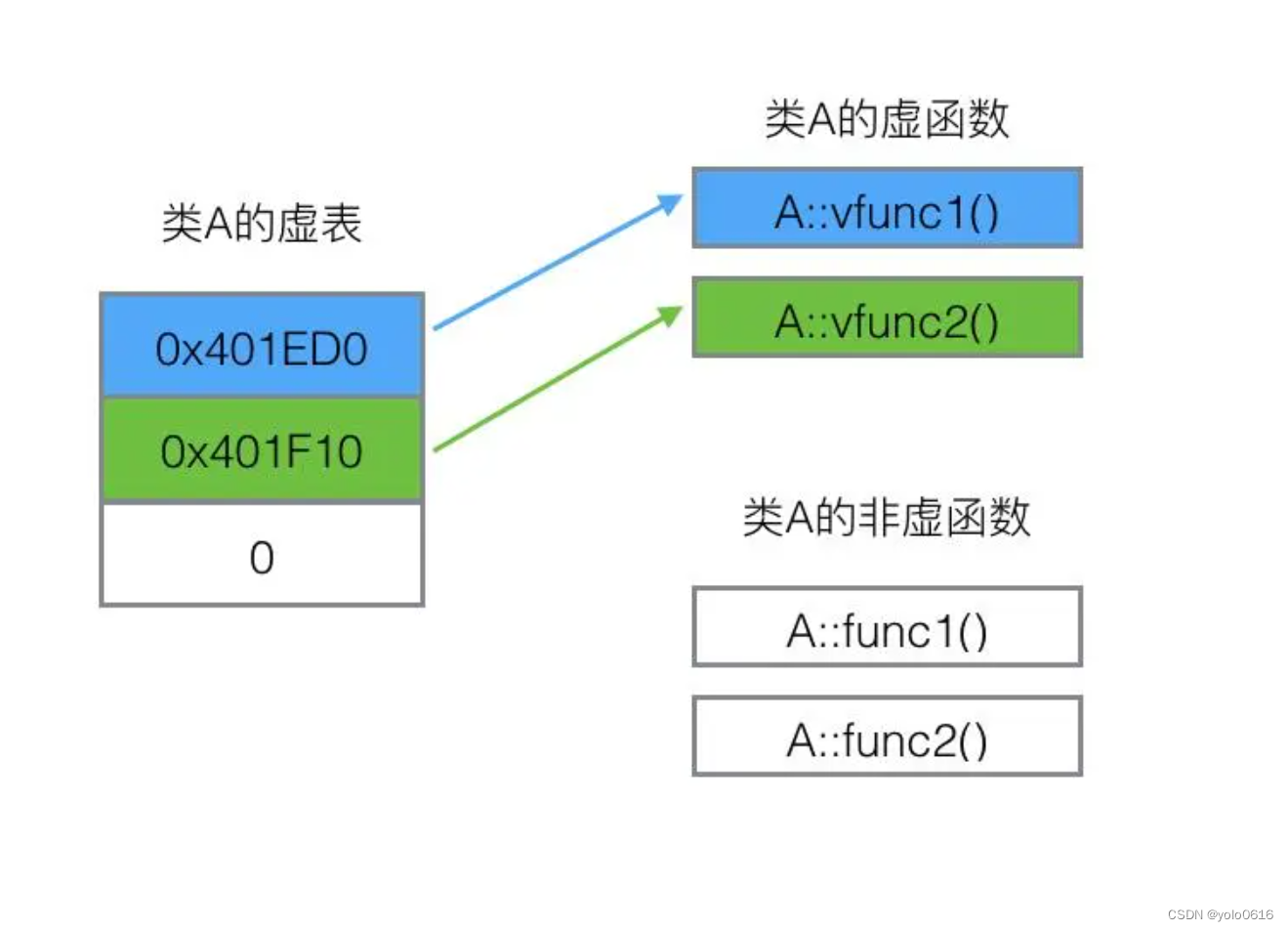
四、2023.9.30.C++面向对象end.4
文章目录 49、 简述一下什么是常函数,有什么作用?50、 说说什么是虚继承,解决什么问题,如何实现?51、简述一下虚函数和纯虚函数,以及实现原理?52、说说纯虚函数能实例化吗,为什么&am…...

【Java】包
package 包(package):其实就是文件夹。 作用:对类进行分类管理。 包的定义格式 格式:package 包名(多级包用 . 分开) 范例:package com.mayikt.demo01 带包的Java类编译和执行 1. 手动建包 安装…...
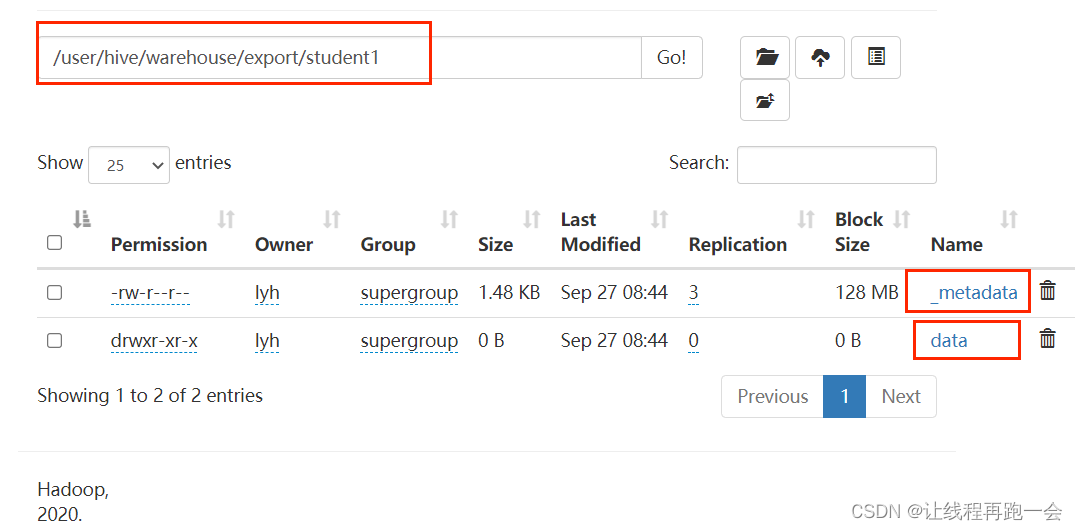
Hive【Hive(二)DML】
启动 hive 命令行: hive DML 数据操作 1、数据导入 1.1、向表中装载数据(load) 语法: hive> load data [local] inpath 数据的path [overwrite] into table student [partition (partcol1val1,…)];(1&#x…...

HTTP的请求方法,空行,body,介绍请求报头的内部以及粘包问题
目录 一、GET与POST简介 二、空行和body 三、初识请求报头以及粘包问题 四、认识请求报头剩余部分 一、GET与POST简介 GET https://www.sogou.com/HTTP/1.1 请求报文中的方法,是最常规的方法(获取资源) POST:传输实体主体的方法…...
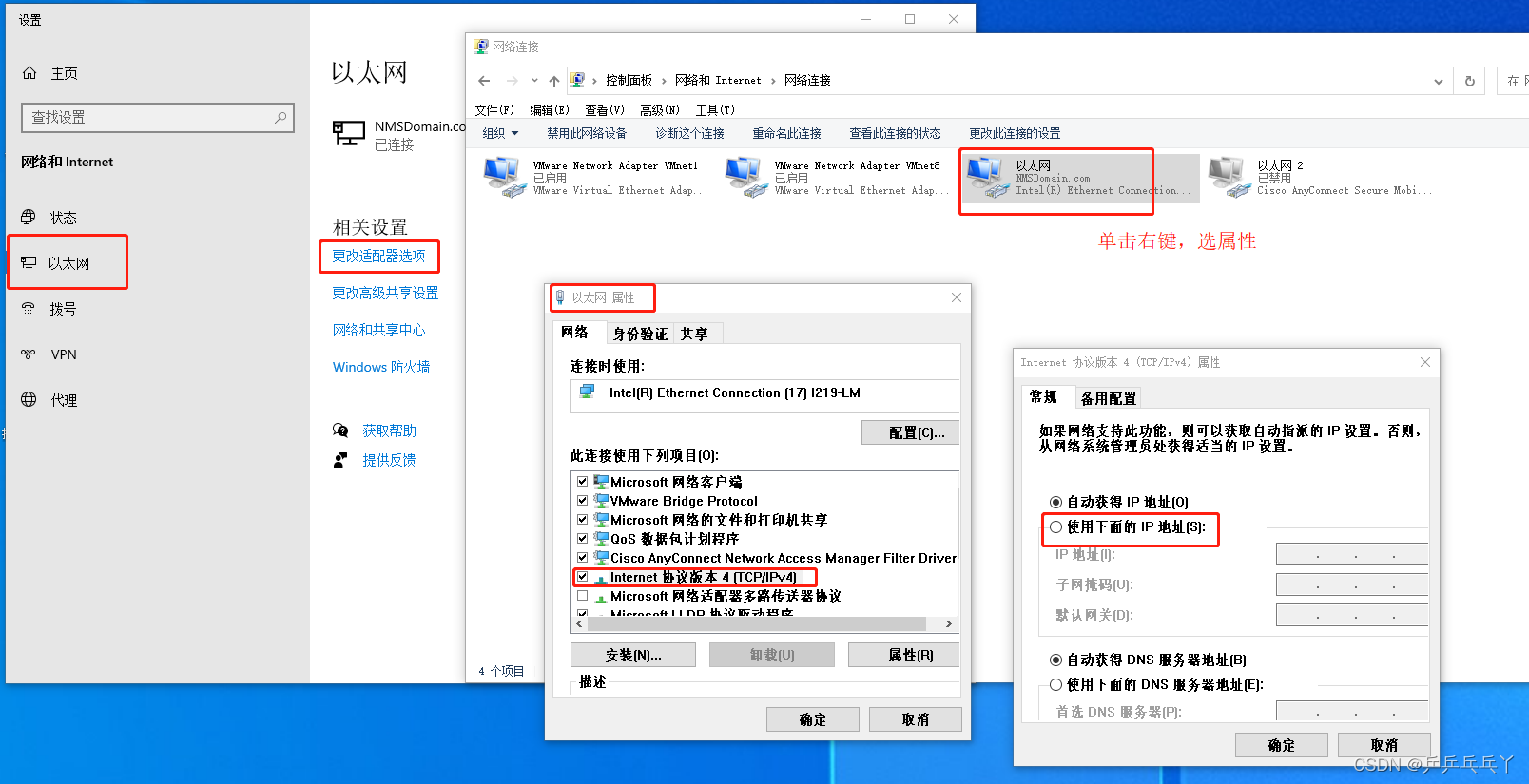
win10 ip设置
百度安全验证...

alibaba dragonwell jdk
阿里巴巴Dragonwell8快速指南 dragonwell-project/dragonwell8 Wiki GitHub 阿里巴巴Dragonwell8用户指南 dragonwell-project/dragonwell8 Wiki GitHub 阿里巴巴Dragonwell8常见问题 dragonwell-project/dragonwell8 Wiki GitHub...
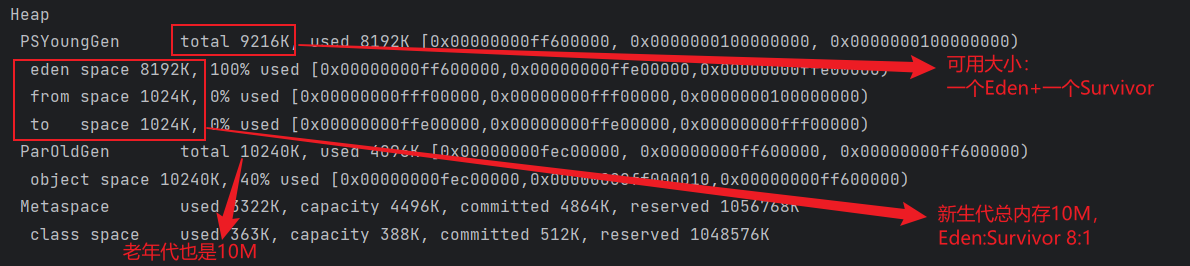
jvm内存分配与回收策略
自动内存管理 解决两个问题 自动给对象分配内存 对象一般堆上分配(而实际上也有可能经过即时编译后被拆散为标量类型并间接地在栈上分配) 新生对象通常会分配在新生代,少数情况下(例如对象大小超过一定阈值)也可能…...

【Vue2和Vue3的双向绑定区别】
Vue2和Vue3的双向绑定区别 vue2 双向绑定原理vue3 双向绑定原理Vue2和Vue3的双向绑定存在以下区别: vue2 双向绑定原理 Vue2 双向绑定的实现主要依赖于 Object.defineProperty() 方法和观察者模式,其中 Object.defineProperty() 方法用于定义属性的 get…...
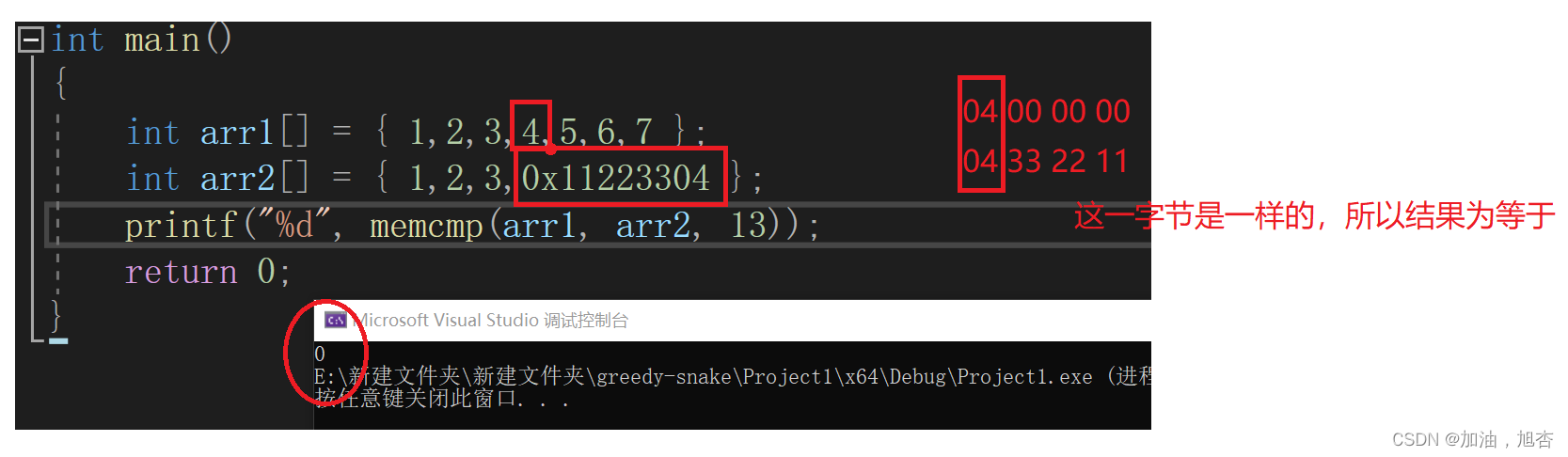
【再识C进阶3(下)】详细地认识字符分类函数,字符转换函数和内存函数
前言 💓作者简介: 加油,旭杏,目前大二,正在学习C,数据结构等👀 💓作者主页:加油,旭杏的主页👀 ⏩本文收录在:再识C进阶的专栏…...
windows WSL配置cuda,pytorch和jupyter notebook
机器配置 GPU: NVIDIA Quadro K2000 与 NVIDIA 驱动程序捆绑的CUDA版本 但按照维基百科的描述,我的GPU对应的compute capability3.0,允许安装的CUDA最高只支持10.2,如下所示。 为什么本地会显示11.4呢?对此,GPT是这…...

回调地狱的产生=>Promise链式调用解决
常见的异步任务包括网络请求、文件读写、定时器等。当多个异步任务之间存在依赖关系,需要按照一定的顺序执行时,就容易出现回调地狱的情况。例如,当一个网络请求的结果返回后,需要根据返回的数据进行下一步的操作,这时…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...