【数据结构】堆的应用-----TopK问题
目录
一、前言
二、Top-k问题
💦解法一:暴力排序
💦解法二:建立N个数的堆
💦解法三:建立K个数的堆(最优解)
三、完整代码和视图
四、共勉
一、前言
在之前的文章中,已经详细的讲解了二叉树、堆、堆排序。那么关于堆还有一个比较有意思的题,就是TopK问题。
如果对堆和二叉树还不够了解的可以看看我之前的文章哦!!!
详解二叉树和堆
二、Top-k问题
Top-k问题:在 N 个数中,找出前 K 个(最大/最小)的元素,一般情况下数据量 N 都远大于 k。
Top-k问题在生活中是非常的常见,比如游戏中某个大区某个英雄熟练度最高的前10个玩家的排名,我们就要根据每个玩家对该英雄的熟练度进行排序,可能有200万个玩家,但我只想选出前10个,要对所有人去排个序吗?显然没这个必要。
再比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
💦解法一:暴力排序
对于Top-K问题,首先想到的最简单直接的方式就是排序。
我们用堆排序,其时间复杂度为:O(N*log2N)。
但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。
💦解法二:建立N个数的堆
建一个 N 个数的堆(C++中可用优先级队列priority_queue),不断的选数,选出前 k 个。
时间复杂度:建N个数的堆为O(N),获取堆顶元素 (也即是最值) 并删除掉堆顶元素为O(log2N),上述操作重复 k 次,所以时间复杂度为O(N+k*log2N)。
【思考】
能否再优化一下呢?假设 N 是 10 亿数,内存中放不下,是放在文件中的。前面两个方法都不能用了。
💦解法三:建立K个数的堆(最优解)
✨基本思想:
用数据集合中前K个元素来建堆。
找前 k 个最大的元素,则建小堆
找前 k 个最小的元素,则建大堆
用剩余的 N-K 个元素依次与堆顶元素来比较,不满足则删除堆顶元素,再插入。
找前 k 个最大的元素,大于堆顶元素,则删除堆顶元素,再插入
找前 k 个最小的元素,小于堆顶元素,则删除堆顶元素,再插入
将剩余的 N-K 个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
✨时间复杂度:▶ 建 k 个元素的堆为O(K);
▶ 遍历剩余的 N-K 个元素的时间代价为O(N-K),假设运气很差,每次遍历都入堆调整;
▶ 入堆调整:删除堆顶元素和插入元素都为O(log2K);
▶ 所以时间复杂度为O(k + (N-K)log2K)。当 N 远大于 K 时,为O(N*log2K),这种解法更优。
✨假如要找出最大的前 10 个数:
▶ 建立 10 个元素的小堆,数据集合中前 10 个元素依次放入小堆,此时的堆顶元素是堆中最小的元素,也是堆里面第 10 个最小的元素,
▶ 然后把数据集合中剩下的元素与堆顶比较,若大于堆顶则去掉堆顶,再将其插入,
▶ 这样一来,堆里面存放的就是数据集合中的前 10 个最大元素,
此时小堆的堆顶元素也就是堆中的第 10 个最大的元素
✨思考:为什么找出最大的前10个数,不能建大堆呢?
如果你建的10个元素的大堆,堆顶元素恰好是数据集合中最大的那个,那第2大的数、第3大的数不就能找不到了。
三、完整代码和视图
以从1w个数里找出最大的前10个数为例:
#include <stdio.h> #include <stdlib.h> #include <assert.h> #include <stdbool.h>typedef int HPDatatype; void Swap(HPDatatype* x, HPDatatype* y) {HPDatatype temp = 0;temp = *x;*x = *y;*y = temp; }void AdjustDown(HPDatatype* a,int n,int parent) {// 左孩子int child = parent * 2 + 1;// 防止越界while (child < n){//小堆if (child + 1 < n && a[child] > a[child + 1]){child++;}// 开始向下调整if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}} }void TopK(HPDatatype* a, int n, int k) {HPDatatype* kminHeap = (HPDatatype*)malloc(sizeof(HPDatatype) * k);assert(kminHeap);// 1. 建堆----用a中前k个元素建堆for (int i = 0; i < k; i++){kminHeap[i] = a[i];}// 建小堆for (int j = ((n - 1) - 1) / 2; j >= 0; j--){// 从倒数第一个非叶子节点开始AdjustDown(kminHeap, k, j);}// 2. 将剩余n-k个元素依次与堆顶的元素交换,比堆顶大,交换for (int i = k; i < n; i++){if (a[i] > kminHeap[0]){kminHeap[0] = a[i];//如果比堆顶大,就替换AdjustDown(kminHeap, k, 0);//向下调整确保为堆}}for (int j = 0; j < k; j++){printf("%d ", kminHeap[j]);}printf("\n");free(kminHeap); }int main() {int n = 10000;int* a = (int*)malloc(sizeof(int) * n);srand(time(0));for (int i = 0; i < n; ++i){a[i] = rand() % 1000000; //产生一个随机数,数值均小于100万}a[5] = 1000000 + 1;a[1231] = 1000000 + 2;a[531] = 1000000 + 3;a[5121] = 1000000 + 4;a[115] = 1000000 + 5;a[2335] = 1000000 + 6;a[9999] = 1000000 + 7;a[76] = 1000000 + 8;a[423] = 1000000 + 9;a[3144] = 1000000 + 10;TopK(a, n, 10);return 0; }
四、共勉
以下就是我对数据结构---堆排序的理解,如果有不懂和发现问题的小伙伴,请在评论区说出来哦,同时我还会继续更新对数据结构-------链式二叉树,请持续关注我哦!!!!

相关文章:

【数据结构】堆的应用-----TopK问题
目录 一、前言 二、Top-k问题 💦解法一:暴力排序 💦解法二:建立N个数的堆 💦解法三:建立K个数的堆(最优解) 三、完整代码和视图 四、共勉 一、前言 在之前的文章中ÿ…...

QT之xml文件的读写
QT之xml文件的读写 简介用法举例 简介 QT的QDomDocument、QDomElement、QDomNode是Qt XML模块中的三个类,用于解析和操作XML文档。 1)QDomDocument类: QDomDocument类表示整个XML文档。它提供了解析XML文档的方法,如setContent(…...

C语言中的异常处理机制是什么?
C语言中的异常处理机制 C语言是一门强大而灵活的编程语言,它为程序员提供了广泛的控制权和自由度。然而,C语言本身并不提供像其他高级语言一样的内置异常处理机制,如Java中的try-catch或Python中的异常处理。因此,C语言程序员需要…...

Java中的并发编程模型和常用工具类
本文主要介绍了Java中的并发编程模型和常用工具类,首先阐述了并发编程的概念及其重要性,然后详细介绍了线程的基本概念、生命周期和状态转换、同步与互斥、死锁问题以及线程池的使用和实现原理。接着介绍了synchronized关键字和Lock接口的使用、原子变量…...
第10章 MySQL(一)
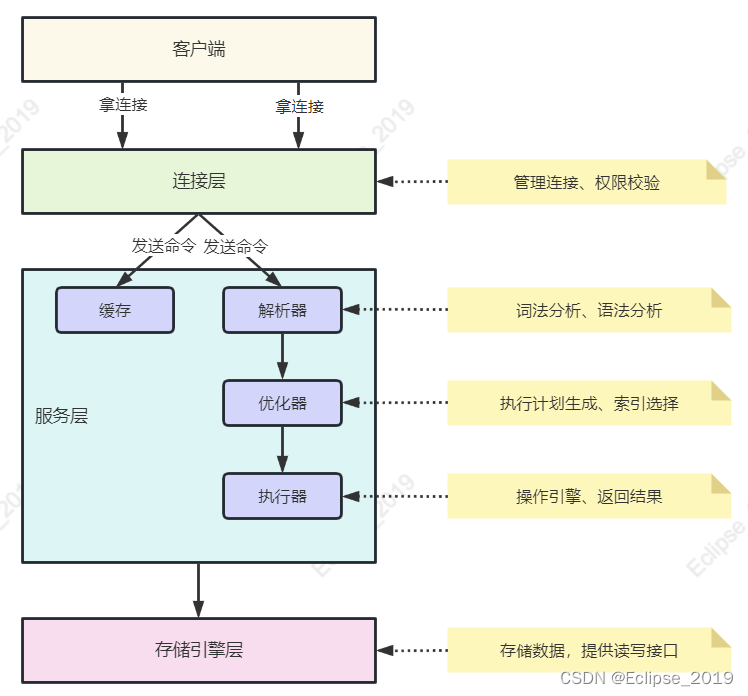
10.1 谈谈MySQL的架构 难度:★★ 重点:★ 白话解析 要想彻底的理解MySQL,它的架构一定要先弄清楚,当Java程序员通过JDBC或者Mybatis去执行一条SQL的时候,到底经历了什么。下边先看一幅图: 户端:Java程序员通过JDBC或者Mybatis去拿MySQL的驱动程序,实际上就是拿客户端。…...
英飞凌 Tricore 架构中断系统详解
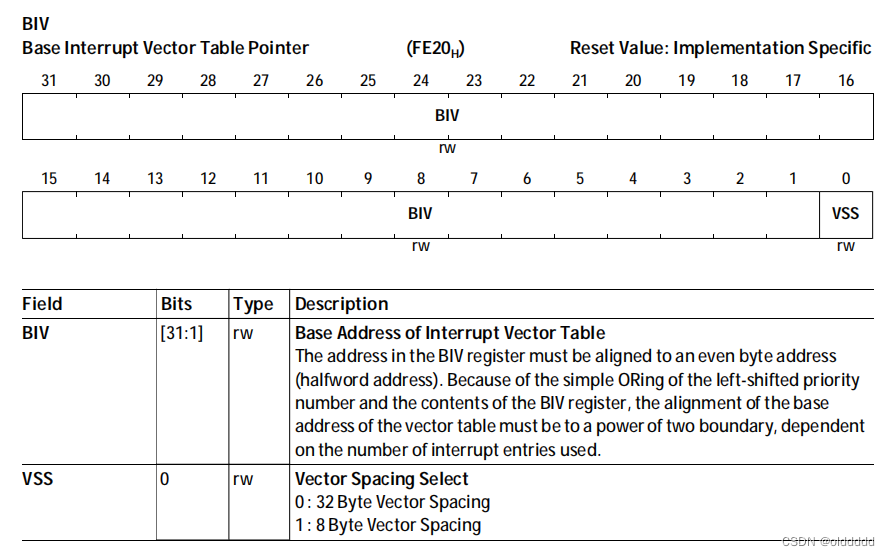
本文以TC3系列MCU为例,先来了解中断源是如何产生的,再看一下CPU是如何处理中断源的。 AURIX TC3XX的中断路由模块 Interrupt Router (IR) 在TC3中,中断既可以被CPU处理,也可以被DMA处理,所以手册中不再把中断称为中断…...

单例模式:饿汉式
单例模式全局仅一个实例,用于获取公共的内容 头文件mglobalinfomgr.h class MGlobalInfoMgr {MGlobalInfoMgr();~MGlobalInfoMgr(); public:static MGlobalInfoMgr* GetInstance(); private:static MGlobalInfoMgr* _instance; }; 源文件mglobalinfomgr.cpp MGl…...

什么是视图
目录 一、什么是视图 二、视图的作用 三、创建视图 四、使用视图 1.使用视图查询员工信息 五、注意事项 六、补充 一、什么是视图 视图是基于查询的虚拟表,是一个逻辑表,本身并不包含数据。同真实的表一样,视图包含一系列带有名称的列…...
C++——list(2)
作者:几冬雪来 时间:2023年9月28日 内容:C——list内容讲解 目录 前言: list的const迭代器: const的iterator: const迭代器: operator->: 拷贝构造: 迭代器接口补充&…...

Django基础讲解-路由控制器和视图(Django-02)
一 路由控制器 参考链接: Django源码阅读:路由(二) - 知乎 Route路由, 是一种映射关系!路由是把客户端请求的 url路径与视图进行绑定 映射的一种关系。 这个/timer通过路由控制器最终匹配到myapp.views中的视图函数 …...

【算法题】2873. 有序三元组中的最大值 I
题目: 给你一个下标从 0 开始的整数数组 nums 。 请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中,找出并返回下标三元组的最大值。如果所有满足条件的三元组的值都是负数,则返回 0 。 下标三元组 (i, j, k) 的值等于 (nums[i]…...

HTML5 跨屏前端框架 Amaze UI
Amaze UI采用国际最前沿的“组件式开发”以及“移动优先”的设计理念,基于其丰富的组件,开发者可通过简单拼装即可快速构建出HTML5网页应用,上线仅半年,Amaze UI就成为了国内最流行的前端框架,目前在Github上收获Star数…...
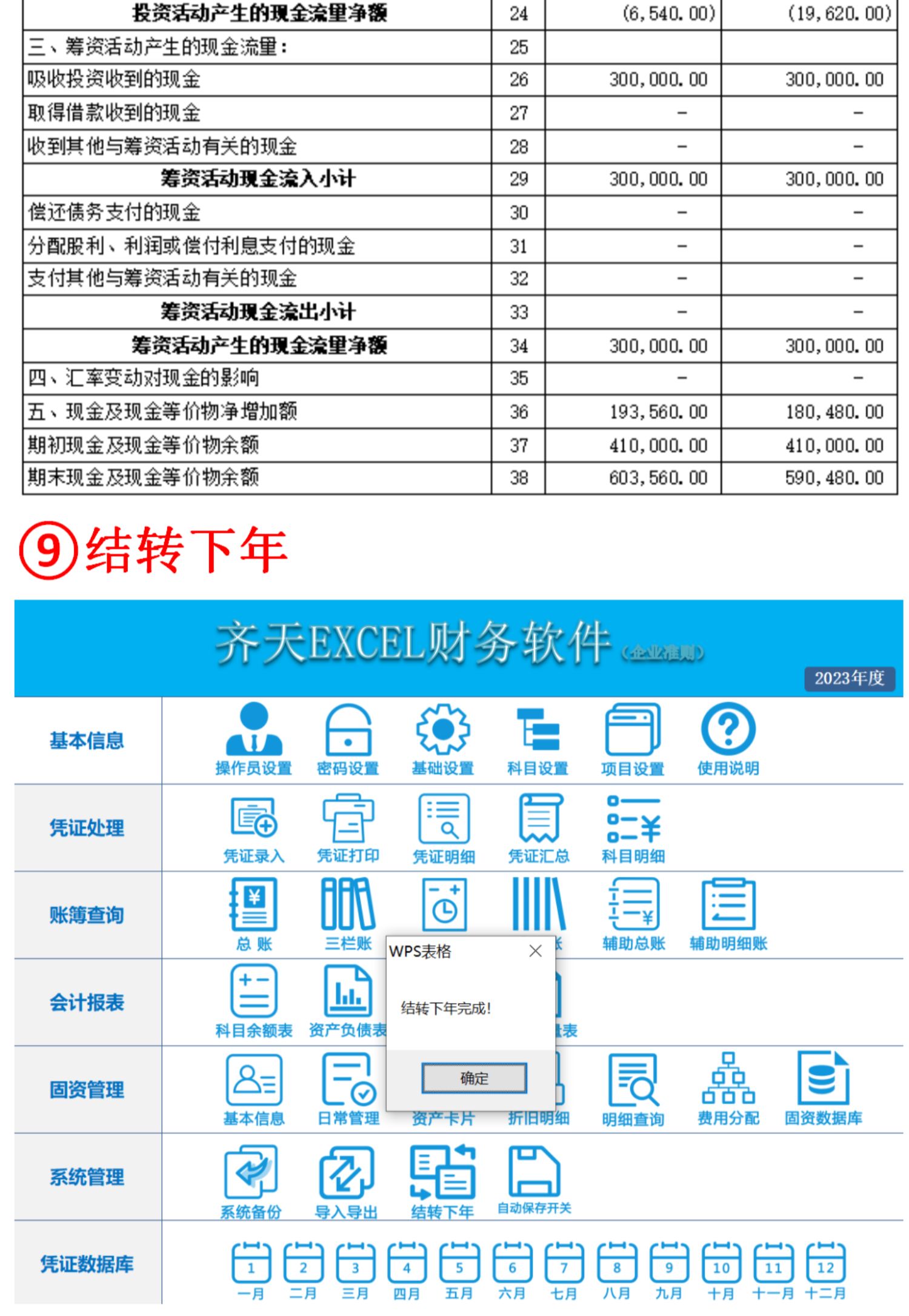
EXCEL会计记账报表财务软件企业公司做账系统凭证自动生成报表
本系统基于VBA编程设计,具有界面简洁美观,操作方便快捷,功能完备实用的特点,系统分为基本信息、凭证处理、账簿查询、会计报表、固定资产管理、系统管理、凭证数据库七大模块,您只需要录入记账凭证,就可以自…...

Can‘t pickle <class ‘__main__.Test‘>: it‘s not the same object as __main__.Test
目录 原因1 类名重复了 案例1 变量名和类名重复 原因1 类名重复了 检查项目代码,是不是其他地方有同名类。 案例1 变量名和类名重复 转自:python3报错Cant pickle <class __main__.Test>: its not the same object as __main__.Test解决 - 知乎…...

第九章 动态规划 part14 1143. 最长公共子序列 1035. 不相交的线 53. 最大子序和
第五十六天| 第九章 动态规划 part14 1143. 最长公共子序列 1035. 不相交的线 53. 最大子序和 一、1143. 最长公共子序列 题目链接: 题目介绍: 思路: 本题和“最长重复子数组”区别在于**这里不要求是连续的了,但要有相对顺序*…...
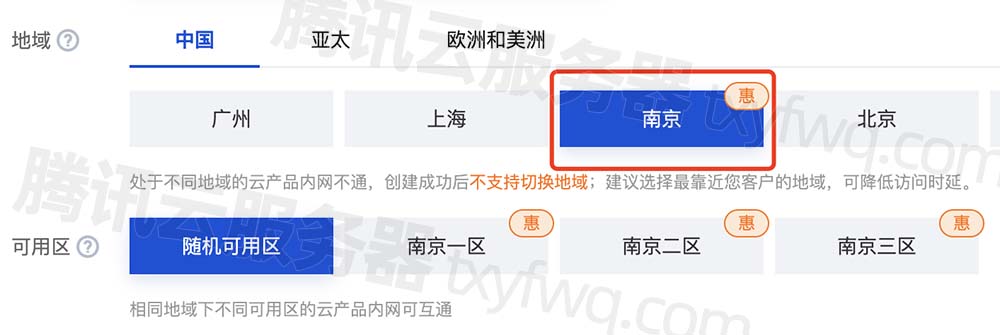
腾讯云服务器南京地域详细介绍、测试IP和Ping值测速
腾讯云服务器南京地域怎么样?南京地域很不错,正好处于中间的位置,南方北方用户均可以选择,网络延迟更低速度更快,并且目前南京地域有活动,南京地域可用区可选南京一区、南京二区和南京三区,腾讯…...

理解CSS的层叠性和继承性
CSS的层叠性(cascading)指的是在同一元素上应用多个样式时,不同样式之间的优先级别以及如何进行组合和冲突解决的规则。具体来说,CSS采用的是“选择器优先级”规则来判断哪个样式优先级更高,如果多个样式的优先级相同&…...
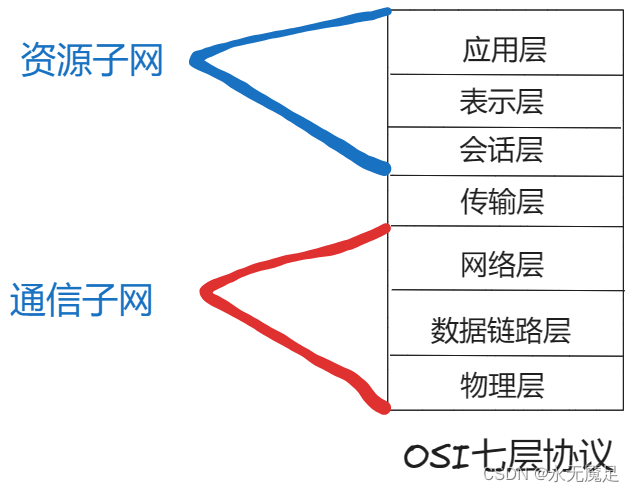
OSI体系结构和TCP/IP体系结构
在第一章( 计网第一章 )的时候,曾经提到过OSI体系结构和TCP/IP体系结构,并对它们进行了简单的对比。这篇博客在其基础上进行更深层次的理解。 一.OSI体系结构: 通信子网: 计算机网络在逻辑功能上可以分为…...

侯捷 C++ STL标准库和泛型编程 —— 8 适配器
8 适配器 适配器 Adapter 只是一个小变化,比如改个接口,函数名称等等其出现在三个地方:仿函数适配器,迭代器适配器,容器适配器可以使用继承 / 复合的两种方式实现,STL中都用复合 其思想就是将该记的东西记…...
)
每日一题 416 分割等和子集(01背包)
题目 分割等和子集 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。 示例 1: 输入:nums [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] …...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

