AtCoder Beginner Contest 233 (A-Ex)
A.根据题意模拟即可
B.根据题意模拟即可
C.直接用map 进行dp即可
D.用前缀和进行模拟,用map统计前缀和,每次计算当前前缀和-k的个数就是以当前点为右端点答案。
E - Σ[k=0..10^100]floor(X/10^k) (atcoder.jp)
(1)题意

(2)思路
手动推一下这个东西就会发现,其实每一位上的贡献等于这一位后面的所有数加起来,因此做一个后缀和即可。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
ll Ans[N],suf[N];
void solve()
{string x;cin >> x;reverse(all(x));for(int i = sz(x) - 1;i >= 0;i --) suf[i] = suf[i + 1] + (x[i] - '0');for(int i = 0;i < sz(x);i ++) {Ans[i] = suf[i]; } for(int i = 0;i < 500001;i ++) {Ans[i + 1] += Ans[i] / 10;Ans[i] %= 10;}int r = 500001;while(Ans[r] == 0) r --;while(r >= 0) cout << Ans[r --];
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}F - Swap and Sort (atcoder.jp)
(1)题意
有一个排列P,给出M组交换关系,第i组swap(Pai,Pbi),问是否有可能可以使P不降。
(2)思路
首先,若i和P[i]不在一个连通块,则一定不会交换成功,然后考虑如何交换,对于度数为1的点说明我们此时交换掉他并且不会影响后继,因此满足拓扑排序,那么我们直接根据拓扑排序进行交换即可。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
struct DSU {vector<int> f,siz;int n;DSU(int _n) {n = _n;f.resize(n + 1);siz.resize(n + 1,1);iota(f.begin(),f.end(),0);}inline int find(int x) {if(x == f[x]) return x;return f[x] = find(f[x]);}inline bool same(int x,int y) {x = find(x),y = find(y);return x == y;}inline void merge(int x,int y) {if(same(x,y)) return ;x = find(x),y = find(y);siz[y] += siz[x];f[x] = y;}//目前连通块个数inline int connect() {int res = 0;for(int i = 1;i <= n;i ++) {res += (i == find(i));}return res;}//求某一个联通块得大小inline int count(int x) {x = find(x);return siz[x];}
};
int p[N],deg[N];
vector<PII> e[N];
vector<int> ans;
inline bool dfs(int u,int f,int tar)
{if(u == tar) return true;for(auto [v,id]: e[u]) {if(v == f) continue;if(dfs(v,u,tar)) {swap(p[u],p[v]);ans.pb(id);return true;}}return false;
}
void solve()
{int n;cin >> n;rep(i,1,n) cin >> p[i];DSU dsu(n);int m;cin >> m;rep(i,1,m) {int u,v;cin >> u >> v;if(!dsu.same(u,v)) {dsu.merge(u,v);e[u].pb({v,i});e[v].pb({u,i});deg[u] ++,deg[v] ++;}}queue<int> q;rep(i,1,n) {if(!dsu.same(i,p[i])) {cout << -1 << '\n';return;}if(deg[i] == 1) q.push(i);}while(!q.empty()) {int v = q.front();q.pop();int tar = 0;for(int i = 1;i <= n;i ++) {if(p[i] == v) {tar = i;break;}}if(!dfs(v,0,tar)) {cout << -1 << '\n';return;}for(auto [u,id]: e[v]) {if(-- deg[u] == 1) q.push(u);}}cout << sz(ans) << '\n';for(auto x : ans) cout << x << ' ';
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}G - Strongest Takahashi (atcoder.jp)
(1)题意
给你一个N*N的矩形,里面#代表的是障碍,.不是障碍,你每次可以选择一个D*D的矩形把里面的障碍清除掉会花费D,问你把N*N的障碍全部清除掉的最小花费是多少。
(2)思路
很明显的一个思路是,这个可以分治进行dp,考虑dp[l1][r1][l2][r2]表示消除[l1-l2][r1-r2]这个矩形的最小花费,我们每一次可以枚举横着切下去还是竖着切下去就行,或者整个是正方形也可以直接清除,取个最小花费即可。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 55;
int dp[N][N][N][N],s[N][N];
string mp[N];
const int inf = 0x3f3f3f3f;
int get(int x1,int y1,int x2,int y2)
{return s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];
}
inline int dfs(int x1,int y1,int x2,int y2)
{if(dp[x1][y1][x2][y2] != -1) return dp[x1][y1][x2][y2];if(get(x1,y1,x2,y2) == 0) return dp[x1][y1][x2][y2] = 0;int mi = inf;for(int i = x1 + 1;i <= x2;i ++) {mi = min(mi,dfs(x1,y1,i - 1,y2) + dfs(i,y1,x2,y2));}for(int i = y1 + 1;i <= y2;i ++) {mi = min(mi,dfs(x1,y1,x2,i - 1) + dfs(x1,i,x2,y2));}if(x2 - x1 == y2 - y1) mi = min(mi,x2 - x1 + 1);return dp[x1][y1][x2][y2] = mi;
}
void solve()
{int n;cin >> n;memset(dp,-1,sizeof(dp));rep(i,1,n) {cin >> mp[i];mp[i] = " " + mp[i];rep(j,1,n) s[i][j] = s[i - 1][j] + s[i][j - 1] + (mp[i][j] == '#') - s[i - 1][j - 1];}cout << dfs(1,1,n,n);
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}Ex - Manhattan Christmas Tree (atcoder.jp)
(1)题意
二维平面上有N棵圣诞树,第i棵位于[xi,yi],要回答一下Q个问题,第i个问题是,以曼哈顿距离为单位,(ai,bi)和距离该点最近的Ki棵圣诞树之间的距离是多少?
(2)思路
考虑曼哈顿距离不好进行计算,因此转换成切比雪夫距离,源坐标系上(x,y)的曼哈顿距离等价于新坐标系上(x+y,x-y)的切比雪夫距离,(补充:源坐标系上(x,y)的切比雪夫距离等价于新坐标系上(,
)的曼哈顿距离)看着切比雪夫距离,我们很容易想到直接二分距离,问题转变这个矩形平面内有多少点,也就是二维数点问题,因为点不是很稠密,我们考虑直接动态开点二维树状数组。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
vector<int> ver[N << 1];
inline int lowbit(int x)
{return x & (-x);
}
inline void add(int x,int y)
{x += N,y += N;if(!y) y = 1;while(y < 2 * N) {ver[y].pb(x);y += lowbit(y);}
}
inline int get(int y,int x1,int x2)
{int Ans = 0;y += N,x1 += N,x2 += N;if(y >= 2 * N) y = 2 * N - 1;while(y > 0) {Ans += upper_bound(all(ver[y]),x2) - lower_bound(all(ver[y]),x1);y -= lowbit(y);}return Ans;
}
inline int query(int x1,int y1,int x2,int y2)
{return get(y2,x1,x2) - get(y1 - 1,x1,x2);
}
void solve()
{vector<PII> point;int n;cin >> n;rep(i,1,n) {int x,y;cin >> x >> y;point.pb({x + y,x - y});}sort(all(point));for(auto [x,y]: point) add(x,y);int q;cin >> q;while(q --) {int x,y,k;cin >> x >> y >> k;int z = x;x = z + y,y = z - y;int l = 0,r = N;while(l <= r) {int m = (l + r) >> 1;if(query(x - m,y - m,x + m,y + m) < k) l = m + 1;else r = m - 1;}cout << l << '\n';}
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}相关文章:
AtCoder Beginner Contest 233 (A-Ex)
A.根据题意模拟即可 B.根据题意模拟即可 C.直接用map 进行dp即可 D.用前缀和进行模拟,用map统计前缀和,每次计算当前前缀和-k的个数就是以当前点为右端点答案。 E - Σ[k0..10^100]floor(X/10^k) (atcoder.jp) (1)…...

解决caffe中的python环境安装的问题
由于caffe(GitHub - BVLC/caffe: Caffe: a fast open framework for deep learning.)使用的python版本是2.7,而非python3,所以安装的时候使用命令:sudo apt install python2.7进行安装。 而在安装python的各种包时&am…...
专业图像处理软件DxO PhotoLab 7 mac中文特点和功能
DxO PhotoLab 7 mac是一款专业的图像处理软件,它为摄影师和摄影爱好者提供了强大而全面的照片处理和编辑功能。 DxO PhotoLab 7 mac软件特点和功能 强大的RAW和JPEG格式处理能力:DxO PhotoLab 7可以处理来自各种相机的RAW格式图像,包括佳能、…...
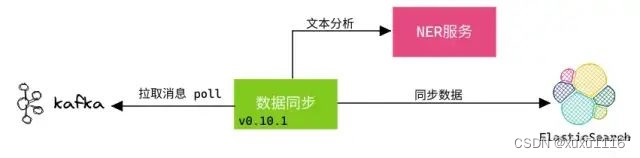
面试题:Kafka 为什么会丢消息?
文章目录 1、如何知道有消息丢失?2、哪些环节可能丢消息?3、如何确保消息不丢失? 引入 MQ 消息中间件最直接的目的:系统解耦以及流量控制(削峰填谷) 系统解耦: 上下游系统之间的通信相互依赖&a…...
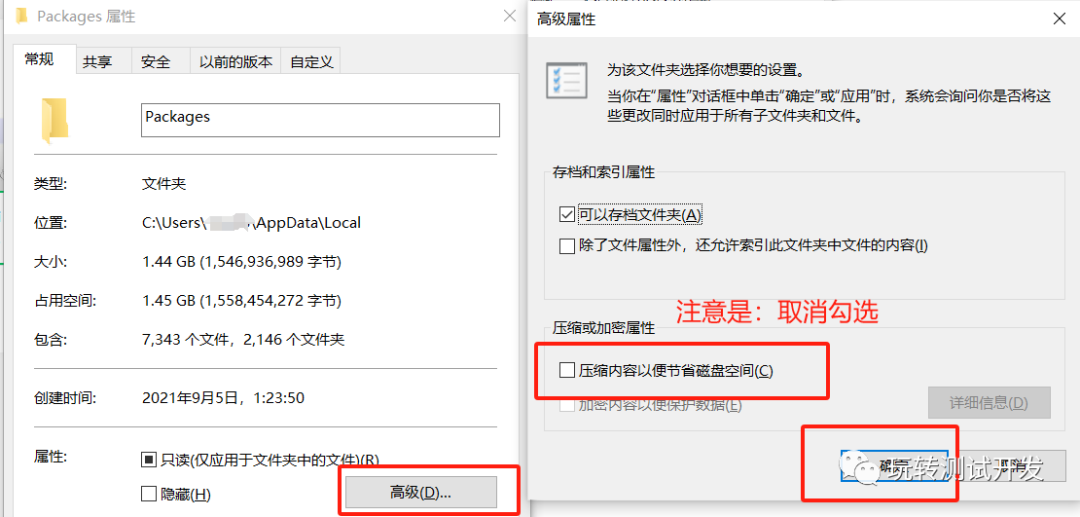
WSL安装异常:WslRegisterDistribution failed with error: 0xc03a001a
简介:如果文件夹右上角是否都有两个相对的蓝色箭头,在进行安装wsl时,设置就会抛出 Installing WslRegisterDistribution failed with error: 0xc03a001a的异常 历史攻略: 卸载WSL WSL:运行Linux文件 WSL࿱…...

【C语言 模拟实现strcmp函数】
C语言程序设计笔记---025 C语言之模拟实现strcmp函数1、介绍strcmp函数2、模拟实现strcmp函数3、结语 C语言之模拟实现strcmp函数 前言: 通过C语言字符串函数的知识,这篇将对strcmp函数进行深入学习底层原理的知识,并模拟实现对应功能。 /知…...

maven 依赖版本冲突异常
maven 依赖版本冲突异常 好巧不巧,前几天刚刚复习完 maven 的内容今天就碰到 maven 报错。 起因是这样的,项目马上快要上线了,在上线之前需要跑一些 audit 去检查项目是否安全(这里主要是 outdated 的依赖检查)。总体…...
11.5-LE Audio 笔记之Context Type)
蓝牙核心规范(V5.4)11.5-LE Audio 笔记之Context Type
专栏汇总网址:蓝牙篇之蓝牙核心规范学习笔记(V5.4)汇总_蓝牙核心规范中文版_心跳包的博客-CSDN博客 爬虫网站无德,任何非CSDN看到的这篇文章都是盗版网站,你也看不全。认准原始网址。!!! 蓝牙中的上下文类型(Context Type)是用于描述音频流当前使用情况或相关使用情…...
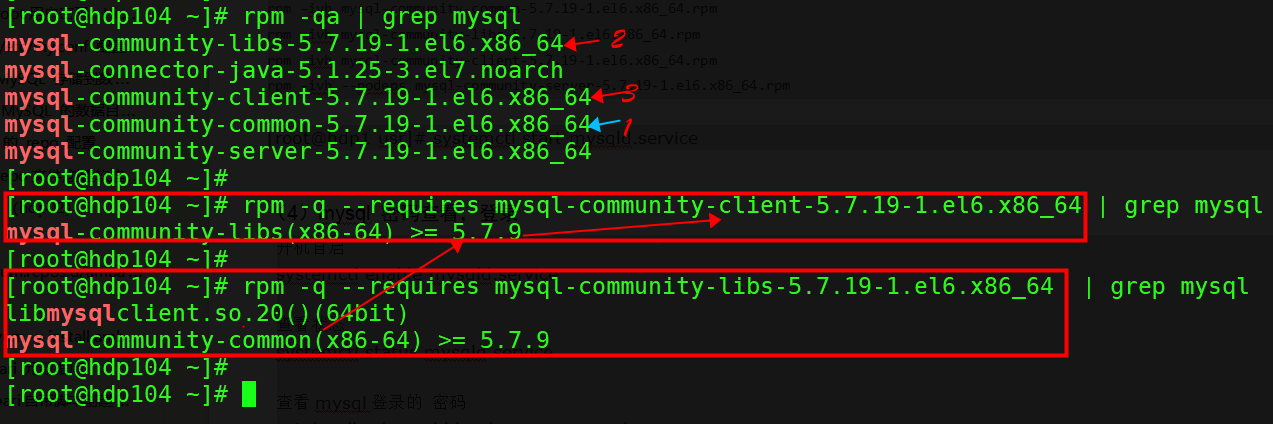
【Linux】RPM包使用详解
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的帮助🌸文…...

勒索病毒最新变种.Elbie勒索病毒来袭,如何恢复受感染的数据?
引言: 网络犯罪正变得越来越隐秘和危险。其中,.Elbie勒索病毒作为数字犯罪的一部分,以其阴险和复杂性而备受关注。本文将带您深入探索.Elbie勒索病毒的工作原理和如何应对这一数字迷宫。如果受感染的数据确实有恢复的价值与必要性࿰…...

ArduPilot开源飞控之AP_Mission
ArduPilot开源飞控之AP_Mission 1. 源由2. AP_Mission类3 简令结构3.1 导航相关3.1.1 jump command3.1.2 condition delay command3.1.3 condition distance command3.1.4 condition yaw command3.1.5 change speed command3.1.6 nav guided command3.1.7 do VTOL transition3.…...

JVM111
JVM1 字节码与多语言混合编程 字节码 我们平时说的java字节码, 指的是用java语言编译成的字节码。准确的说任何能在jvm平台上执行的字节码格式都是一样的。所以应该统称为:jvm字节码。不同的编译器,可以编译出相同的字节码文件,字节码文件…...

排序篇(三)----交换排序
排序篇(三)----交换排序 1.冒泡排序 基本思想: 通过不断地比较相邻的元素,将较大的元素往后移动,从而实现排序的目的。 具体的步骤如下: 从待排序的数组中选择相邻的两个元素进行比较,如果前一个元素大于后一个元素&#…...

React antd Table点击下一页后selectedRows丢失之前页选择内容的问题
一、问题 使用了React antd 的<Table>标签,是这样记录选中的行id与行内容的: <TabledataSource{data.list}rowSelection{{selectedRowKeys: selectedIdsInSearchTab,onChange: this.onSelectChange,}} // 表格是否可复选,加 type: …...
11.4-LE Audio 笔记之音频模型)
蓝牙核心规范(V5.4)11.4-LE Audio 笔记之音频模型
专栏汇总网址:蓝牙篇之蓝牙核心规范学习笔记(V5.4)汇总_蓝牙核心规范中文版_心跳包的博客-CSDN博客 爬虫网站无德,任何非CSDN看到的这篇文章都是盗版网站,你也看不全。认准原始网址。!!! 从一开始,蓝牙低功耗(Bluetooth Low Energy,BLE)音频的开发就秉持着“以设…...

Spring Boot:利用JPA进行数据库的查删
目录标题 DAO 、Service 、 Controller 层控制器文件示例代码-单个查找查找成功示例代码-列表查找查找成功示例代码-删除删除成功 DAO 、Service 、 Controller 层 DAO 层负责数据库访问,它封装了对数据库的访问操作,例如查询、插入、更新和删除等。 Q…...

1711: 【穷举】满足条件的整数
题目描述 假设a、b、c均为整数(1<a,b,c<100),同时a<b,找出所有符合条件:a2 b2 n*c3的整数组。 按a从小到大的顺序输出所有满足条件的整数组(若a相同,则按b从小到大的顺序输出) 输入…...

【数据结构】堆的应用-----TopK问题
目录 一、前言 二、Top-k问题 💦解法一:暴力排序 💦解法二:建立N个数的堆 💦解法三:建立K个数的堆(最优解) 三、完整代码和视图 四、共勉 一、前言 在之前的文章中ÿ…...

QT之xml文件的读写
QT之xml文件的读写 简介用法举例 简介 QT的QDomDocument、QDomElement、QDomNode是Qt XML模块中的三个类,用于解析和操作XML文档。 1)QDomDocument类: QDomDocument类表示整个XML文档。它提供了解析XML文档的方法,如setContent(…...

C语言中的异常处理机制是什么?
C语言中的异常处理机制 C语言是一门强大而灵活的编程语言,它为程序员提供了广泛的控制权和自由度。然而,C语言本身并不提供像其他高级语言一样的内置异常处理机制,如Java中的try-catch或Python中的异常处理。因此,C语言程序员需要…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
