多源最短路径的原理及C++实现
时间复杂度
O(n3),n是端点数。
核心代码
template<class T, T INF = 1000 * 1000 * 1000>
class CNeiBoMat
{
public:
CNeiBoMat(int n, const vector<vector<int>>& edges,bool bDirect=false,bool b1Base= false)
{
m_vMat.assign(n, vector<int>(n, INF));
for (int i = 0; i < n; i++)
{
m_vMat[i][i] = 0;
}
for (const auto& v : edges)
{
m_vMat[v[0]- b1Base][v[1]- b1Base] = v[2];
if (!bDirect)
{
m_vMat[v[1]- b1Base][v[0]- b1Base] = v[2];
}
}
}
vector<vector<int>> m_vMat;
};
//多源码路径
template<class T,T INF = 1000*1000*1000>
class CFloyd
{
public:
CFloyd(const vector<vector<T>>& mat)
{
m_vMat = mat;
const int n = mat.size();
for (int i = 0; i < n; i++)
{//通过i中转
for (int i1 = 0; i1 < n; i1++)
{
for (int i2 = 0; i2 < n; i2++)
{
//此时:m_vMat[i1][i2] 表示通过[0,i)中转的最短距离
m_vMat[i1][i2] = min(m_vMat[i1][i2], m_vMat[i1][i] + m_vMat[i][i2]);
//m_vMat[i1][i2] 表示通过[0,i]中转的最短距离
}
}
}
};
vector<vector<T>> m_vMat;
};
原理
当一层循环执行完后,m_vMat[i1][i2]表示经过[0,i)中的任意个点的最短距离。
初始状态下, m_vMat[i1][i2]表示直达的最小距离,也就是经过0个点。
通过[0,i)中任意个点,i1到i2的最短路径记为PrePathi1i2,通过[0,i+1)中任意个点,i1到i2的距离的路径为Pathi1i2,如果Path不经过Pathi1i2,则和PrePathi1i2相同。如果经过则可以拆分成{i1…i}+{i…i2},显然{i1…i}是PrePathi1i,{i…i2}是PrePathii2,否则替换成PrePathi1i和PrePathii2。
m_vMat同时表示PreMath和Math,如果m_vMat[i1][i]或m_vMat[i][i2]已经更新,会带来错误的结果么?结果是不会,会更新但值不变。
当i1等于i时:
m_vMat[i][i2] = min(…, m_vMat[i][i] + m_vMat[i][i2]);
由于m_vMat[i][i]为0,所以右式就是左式。
当i2等于i时,类似。
样例
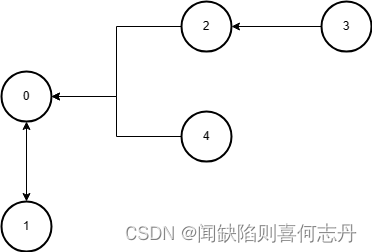
假定有5个点,前4个点连通。整个处理流程如下:
| 初始状态 | 处理完i等于0(不变) | |||||||||
| 0 | 1 | 4 | INF | INF | ||||||
| 1 | 0 | 2 | 4 | INF | ||||||
| 4 | 2 | 0 | 3 | INF | ||||||
| INF | 4 | 3 | 0 | INF | ||||||
| INF | INF | INF | INF | 0 | ||||||
| 处理完i等于1 | 处理完i等于2(不变) | |||||||||
| 3 | 5 | |||||||||
| 3 | ||||||||||
| 5 | ||||||||||
| 处理完i等于3,结果不变 | 最终结果 | |||||||||
| 0 | 1 | 3 | 5 | INF | ||||||
| 1 | 0 | 2 | 4 | INF | ||||||
| 3 | 2 | 0 | 3 | INF | ||||||
| 5 | 4 | 3 | 0 | INF | ||||||
| INF | INF | INF | INF | 0 | ||||||
测试样例
#include <vector>
#include<assert.h>
using namespace std;
struct CDebugParam
{
int n;
vector<vector<int>> edges;
vector<vector<int>> result;
};
int main()
{
const int INF = 1000 * 1000 * 1000;
vector<CDebugParam> params = { {5,{{0,1,1},{0,2,4},{1,2,2},{1,3,4},{2,3,3}},
{
{0,1,3,5,INF},
{1,0,2,4,INF},
{3,2,0,3,INF},
{5,4,3,0,INF},
{INF,INF,INF,INF,0}
}
} };
for (const auto& param : params)
{
CNeiBoMat<int> mo(param.n, param.edges);
CFloyd<int> floyd(mo.m_vMat);
for (int r = 0; r < param.n; r++)
{
for (int c = 0; c < param.n; c++)
{
assert(param.result[r][c] == floyd.m_vMat[r][c]);
}
}
}
}
其它
测试环境
win7 VS2019 C++17
源码及测试样例下载
https://download.csdn.net/download/he_zhidan/88393631
doc文档下载
https://download.csdn.net/download/he_zhidan/88348653
相关文章:

多源最短路径的原理及C++实现
时间复杂度 O(n3),n是端点数。 核心代码 template<class T, T INF 1000 * 1000 * 1000> class CNeiBoMat { public: CNeiBoMat(int n, const vector<vector<int>>& edges,bool bDirectfalse,bool b1Base false) { m_vMat.assign(n, vector<…...
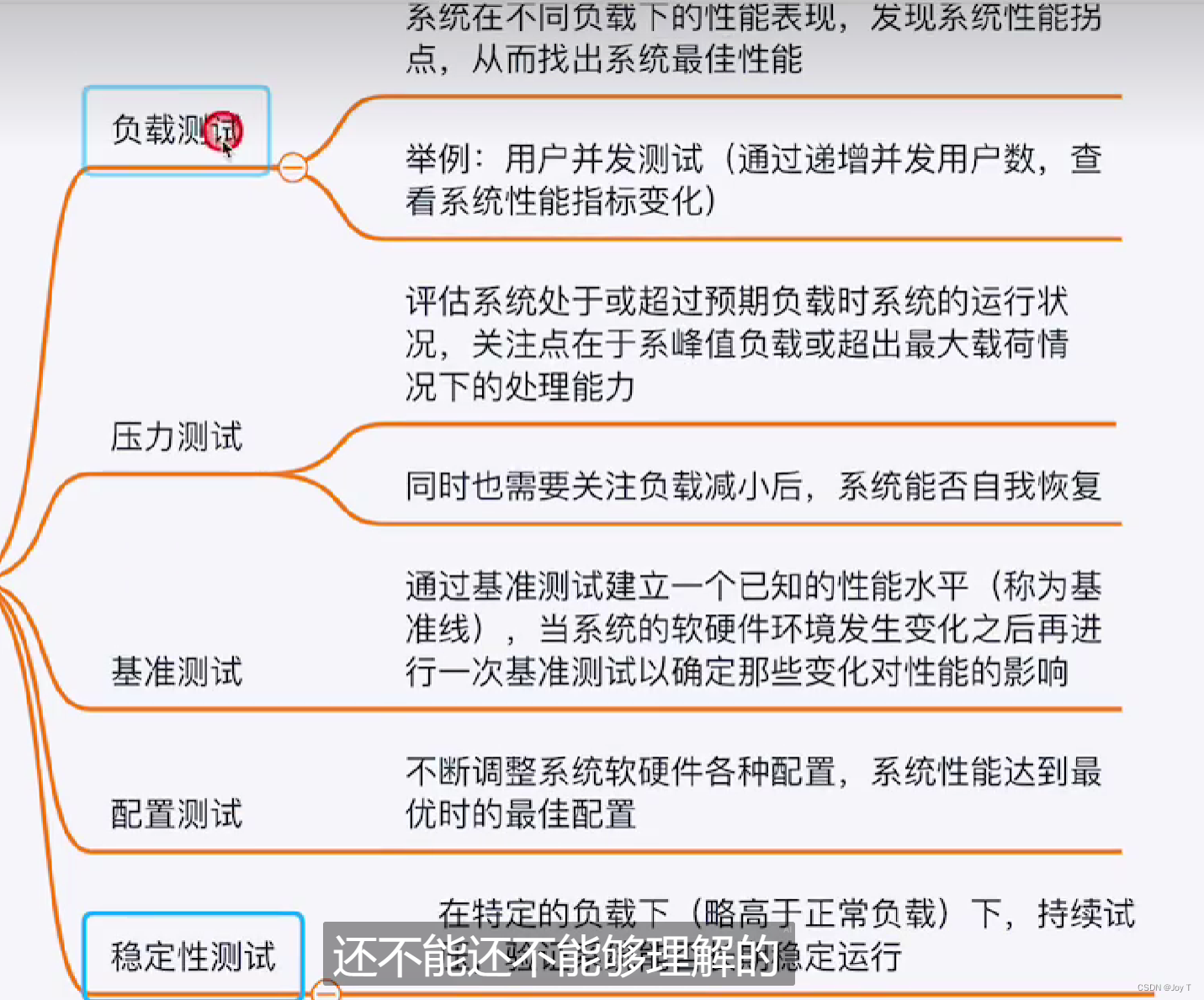
JMeter性能测试
性能测试前言 老师开局一句话:性能测试和你会不会JMeter一点关系没有…… 作者坚持技多不压身的原则,还是多学一点JMeter吧,看老师到底要怎么讲下去,什么并发量、吞吐量啥的…… 性能测试的核心思想:在于创造大量并发去…...

Cocos Creator3.8 实战问题(四)巧用九宫格图像拉伸
一、为什么要使用九宫格图像拉伸 相信做过前端的同学都知道,ui (图片)资源对包体大小和内存都有非常直接的影响。 通常ui 资源都是图片,也是最占资源量的资源类型,游戏中的ui 资源还是人机交互的最重要的部分ÿ…...
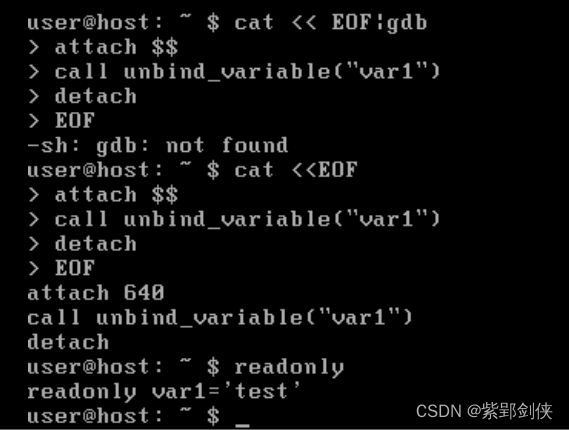
Linux shell编程学习笔记7:只读变量
在编程过程中,我们经常会使用到一些常量,也就是值不需要改变的变量,在许多编程语言提供了常量的定义方式,比如c/c的define MAXNUM 99999 或 const int a 7,javasccipt的const a7, 等等。 跟以上这些方法…...

Scala第十七章节
Scala第十七章节 scala总目录 文档资料下载 章节目标 了解集合的相关概念掌握Traversable集合的用法掌握随机学生序列案例 1. 集合 1.1 概述 但凡了解过编程的人都知道程序 算法 数据结构这句话, 它是由著名的瑞士计算机科学家尼古拉斯沃斯提出来的, 而他也是1984年图灵…...
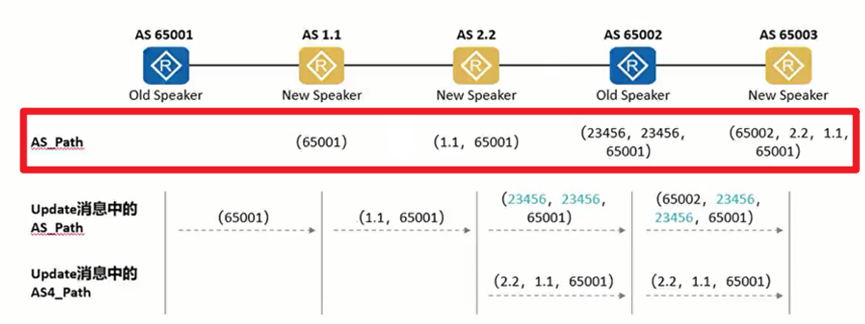
BGP高级特性——4字节AS号
目录 4字节AS号 相关概念 两种过渡属性 4字节AS号的格式 4字节AS号建立邻居 4字节AS号路由传递 配置命令 4字节AS号 相比于2字节AS号,范围更大。由1~65535扩展到1~4294967295 支持4字节AS号的BGP设备兼容仅支持2字节AS号的BGP设备 相关概念 Speaker&#…...
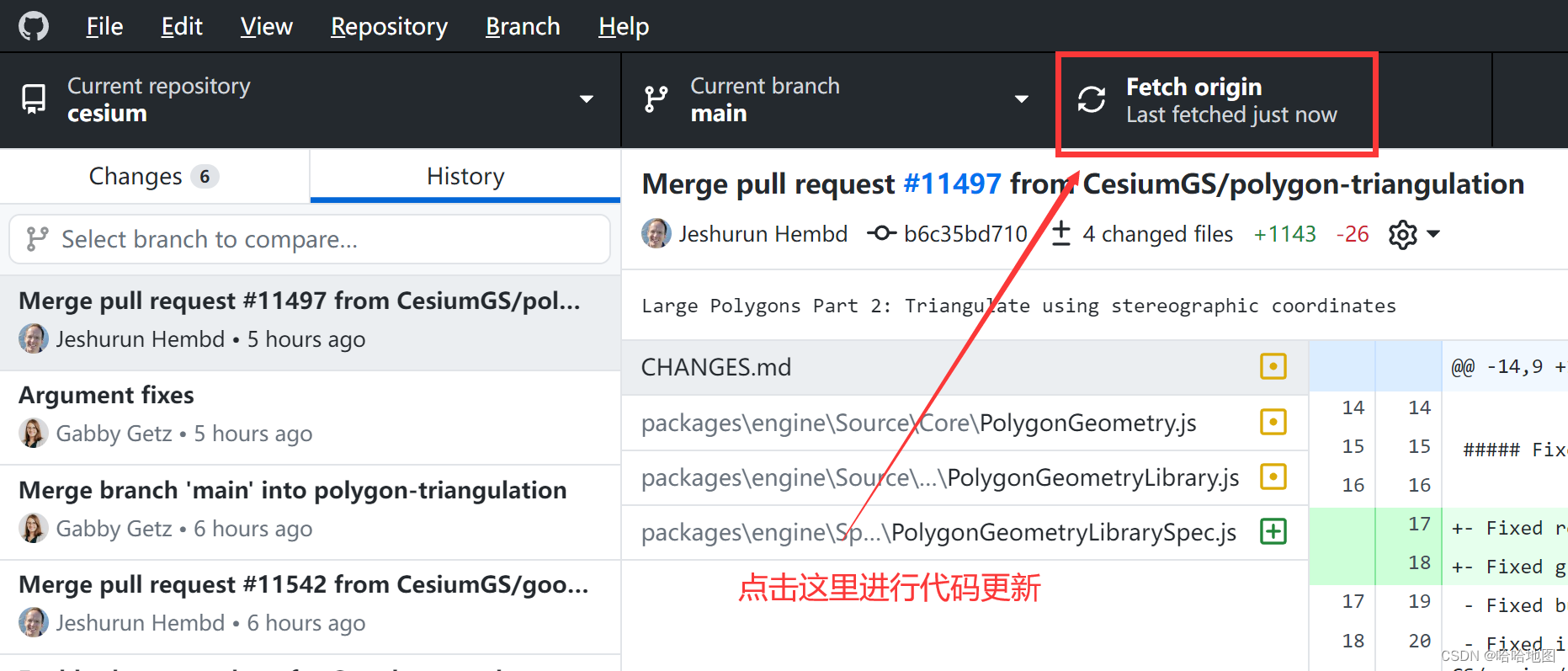
cesium源码无法更新的解决方案
一、环境: 中国移动的宽带 win10操作系统 二、问题复现步骤: 1、开了VPN,设置为全局代理 2、在vscode中执行git pull命令 3、结果显示无法更新 三、解决方案: 1、安装Github官方开发的软件Github Desktop 下载地址…...

大数据-玩转数据-双流JOIN
一、双流JOIN 在Flink中, 支持两种方式的流的Join: Window Join和Interval Join 二、Window Join 窗口join会join具有相同的key并且处于同一个窗口中的两个流的元素. 注意: 1.所有的窗口join都是 inner join, 意味着a流中的元素如果在b流中没有对应的, 则a流中这个元素就不会…...

from PIL import Image,文字成图,ImageFont import jieba分词,input优雅python绘制图片
开始的代码 import os from PIL import Image, ImageDraw, ImageFont import jiebadef generate_image_with_white_bg(text, font_path, output_path):# 设置图片大小和背景颜色image_width 800image_height 600bg_color (255, 255, 255) # 白色# 创建图片对象image Imag…...

渗透测试信息收集方法笔记
一、指纹识别 1、钟馗之眼https://www.zoomeye.org/ 2、天眼查https://www.tianyancha.com/ 3、工具:御剑WEB指纹识别系统正式版,可以查网站用了哪些框架,什么版本,有哪些漏洞 4、kali whatweb 二、信息泄露 1、csdn https://www.…...

协议栈——连接服务器
如对方的ip和port配置信息,这里的连接是指通信前的准备工作 上一篇介绍查看套接字的命令时,可以看到很多信息,但是刚刚创建出来的套接字是什么信息都没有的,协议栈也因此不知道和谁通信; 客户端填补信息 这一步中调…...
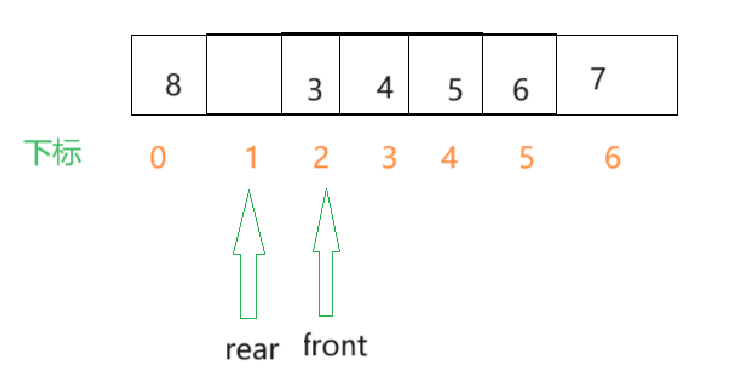
数据结构--队列与循环队列的实现
数据结构–队列的实现 1.队列的定义 比如有一个人叫做张三,这天他要去医院看病,看病时就需要先挂号,由于他来的比较晚,所以他的号码就比较大,来的比较早的号码就比较小,需要到就诊窗口从小号到大依次排队,前面的小号就诊结束之后,才会轮到大号来,小号每就诊完毕就销毁,每新来…...
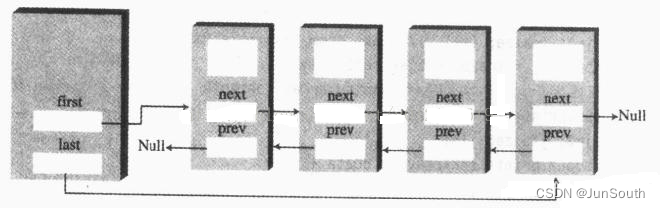
数据结构—栈、队列、链表
一、栈 Stack(存取O(1)) 先进后出,进去123,出来321。 基于数组:最后一位为栈尾,用于取操作。 基于链表:第一位为栈尾,用于取操作。 1.1、数组栈 /*** 基于数组实现的顺序栈&#…...

2023年4月到7月工作经历
2023年4 有同事说程序崩溃一起分析得结果 unsigned uNum 2; std::string str "abc" uNum; std::cout << str; 结果是c 。如果uNum 很大的话,就可能崩溃。 unsigned uNum 2; //std::string str "abc" uN…...
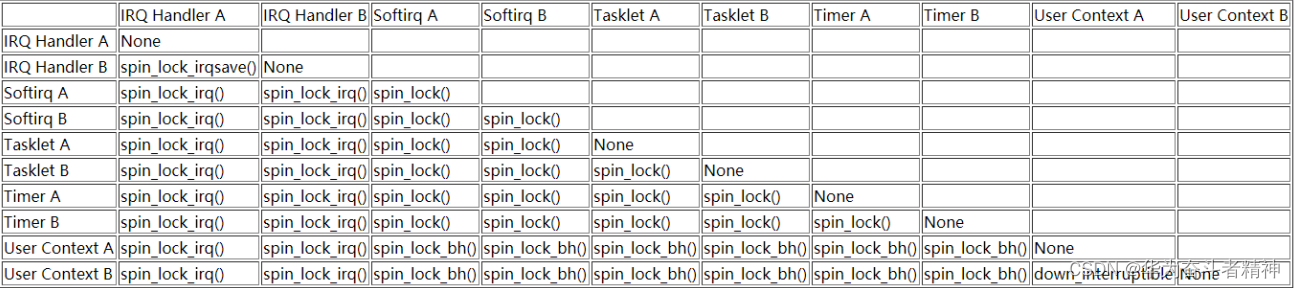
嵌入式Linux应用开发-驱动大全-同步与互斥③
嵌入式Linux应用开发-驱动大全-同步与互斥③ 第一章 同步与互斥③1.4 Linux锁的介绍与使用1.4.1 锁的类型1.4.1.1 自旋锁1.4.1.2 睡眠锁 1.4.2 锁的内核函数1.4.2.1 自旋锁1.4.2.2 信号量1.4.2.3 互斥量1.4.2.4 semaphore和 mutex的区别 1.4.3 何时用何种锁1.4.4 内核抢占(pree…...

力扣-383.赎金信
Idea 使用一个hashmap 或者一个int数组存储第二次字符串中每一个字符及其出现的次数 遍历第一个字符串,讲出现的重复字符减1,若该字符次数已经为0,则返回false AC Code class Solution { public:bool canConstruct(string ransomNote, strin…...
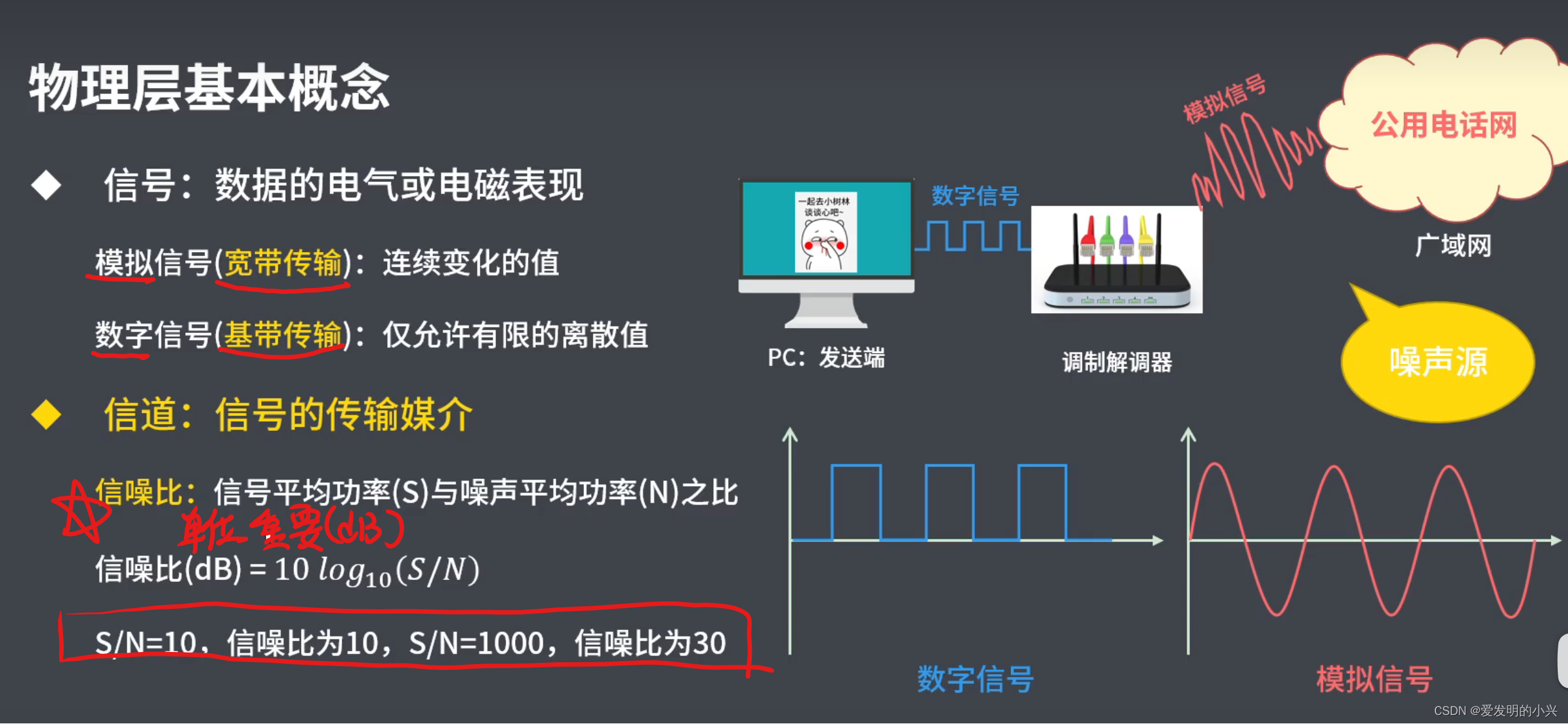
计算机网络 第二章物理层
计算机网络第二章知识点速刷 其中重要的是信源和信宿,以及调制解调器在通信模型当中起到的作用。...

uniapp:动态修改页面标题
我们经常遇到这种情况,点击新增按钮,进入一个空白表单页面,点击修改按钮,其实也是进入这个表单页面,只是表单内容已经被数据库的记录反显了,为了区别页面,我们还需要动态设置页面的标题…...
java学生管理系统
一、项目概述 本学生管理系统旨在提供一个方便的界面,用于学校或机构管理学生信息,包括学生基本信息、课程成绩等。 二、系统架构 系统采用经典的三层架构,包括前端使用JavaSwing,后端采用Java Servlet,数据库使用M…...

Docker和容器化:简介和使用案例
Docker和容器化:简介和使用案例 引言 容器化技术在近年来变得越来越流行,为开发人员和运维团队提供了更加灵活、高效的软件部署和管理方式。其中,Docker是最为知名和广泛使用的容器化平台之一。本篇博客文章将介绍Docker和容器化的基本概念…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
