怒刷LeetCode的第23天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:贪心算法
方法二:动态规划
方法三:回溯算法
方法四:并查集
第二题
题目来源
题目内容
解决方法
方法一:排序和遍历
方法二:扫描线算法
方法三:栈
第三题
题目来源
题目内容
解决方法
方法一:遍历和比较
第一题
题目来源
55. 跳跃游戏 - 力扣(LeetCode)
题目内容

解决方法
方法一:贪心算法
这个算法使用贪心的思想,通过遍历数组中的每个元素,始终保持一个能够跳到的最远位置 maxPos。在遍历过程中,如果当前位置超过了 maxPos,则说明无法继续跳跃,返回 false。否则,更新 maxPos 的值,将其与 i + nums[i] 比较,取较大值作为新的 maxPos。最后判断 maxPos 是否已经超过或等于最后一个下标,如果是,则返回 true,否则返回 false。
class Solution {
public boolean canJump(int[] nums) {int n = nums.length;int maxPos = 0; // 当前能够跳到的最远位置for (int i = 0; i < n; i++) {if (i > maxPos) {// 如果当前位置超过了能够跳到的最远位置,说明无法继续跳跃,返回falsereturn false;}maxPos = Math.max(maxPos, i + nums[i]);// 更新能够跳到的最远位置if (maxPos >= n - 1) {// 如果能够跳到的最远位置已经超过或等于最后一个下标,说明可以到达最后一个下标,返回truereturn true;}}return false;
}}复杂度分析:
- 时间复杂度为 O(n),其中 n 是数组的长度。因为我们只需遍历一次数组即可判断能否到达最后一个下标。
- 空间复杂度为 O(1),我们只需要保存一个额外的变量 maxPos。
LeetCode运行结果:
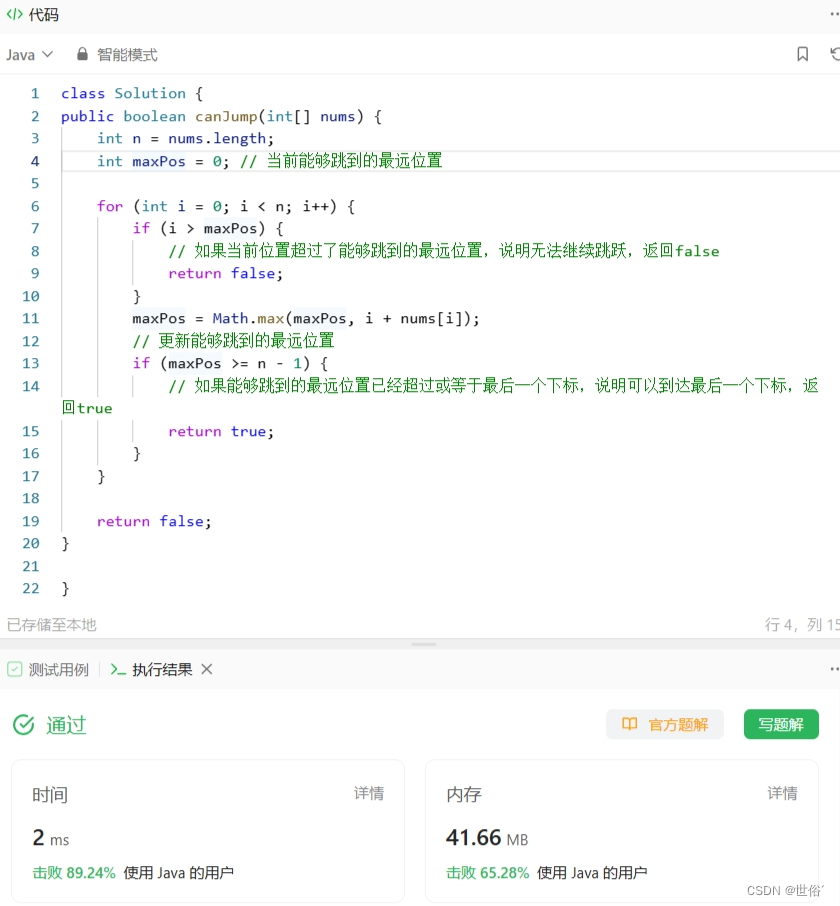
方法二:动态规划
除了贪心之外,还可以使用动态规划来解决这个问题。
该算法使用动态规划的思想,定义一个布尔型数组 dp,其中 dp[i] 表示能否从第0个位置跳到第i个位置。
为了计算 dp[i],我们从前往后遍历数组中的每个位置 i,并在其中再次遍历所有位置 j < i。只有当某个位置 j 可以到达,并且从 j 位置可以到达 i 位置时,才有可能到达 i 位置。因此,如果存在一个位置 j 满足条件,即 dp[j] && j + nums[j] >= i,则说明当前位置 i 可以到达,我们将 dp[i] 设置为 true。最终返回 dp[n-1] ,表示能否从第 0 个位置跳到最后一个位置。
class Solution {
public boolean canJump(int[] nums) {int n = nums.length;boolean[] dp = new boolean[n]; // dp[i] 表示能否从第0个位置跳到第i个位置dp[0] = true; // 第0个位置一定可以到达for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (dp[j] && j + nums[j] >= i) {// 如果前面某一个位置可以到达,并且这个位置可以到达i,那么说明i也可以到达dp[i] = true;break;}}}return dp[n - 1];
}
}复杂度分析:
- 时间复杂度为 O(n^2),因为在计算 dp[i] 时,需要遍历之前的所有位置 j,所以总共需要进行 n * (n-1) / 2 次比较。
- 空间复杂度方面,动态规划算法使用了一个长度为 n 的数组 dp,所以空间复杂度为 O(n)。
与贪心算法相比,动态规划算法的时间复杂度较高,但是更加直观易懂,且可以解决更一般化的跳跃游戏问题。
LeetCode运行结果:
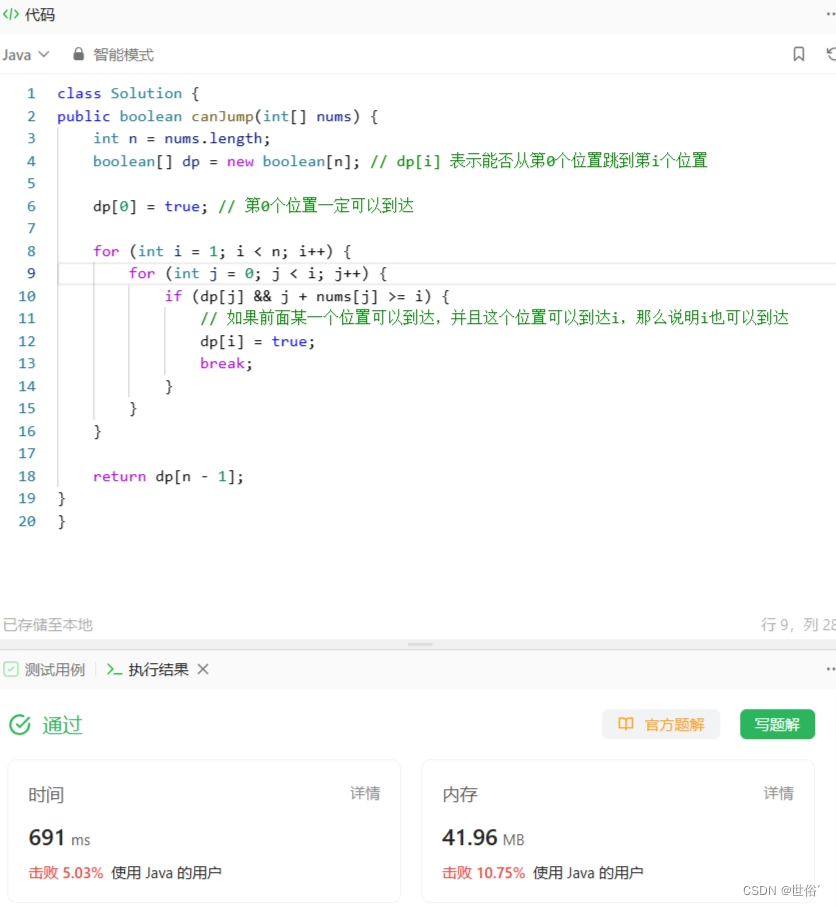
方法三:回溯算法
除了贪心算法和动态规划算法,还可以使用回溯算法来解决跳跃游戏问题。
该算法使用回溯的思想,在每个位置上探索所有可能的跳跃,直到找到能到达最后一个位置的路径,或者发现无法到达的情况。
具体实现中,我们定义一个辅助函数 backtrack,其中 position 参数表示当前所在的位置。首先,在每个位置上计算能够跳跃到的最远位置 furthestJump,然后从最远位置开始反向遍历,尝试从当前位置跳到下一个位置 nextPosition,并递归调用 backtrack 函数。如果最终找到一条路径能够到达最后一个位置,则返回 true;如果所有尝试都失败,则返回 false。
class Solution {
public boolean canJump(int[] nums) {return backtrack(nums, 0);
}private boolean backtrack(int[] nums, int position) {// 到达最后一个位置,返回 trueif (position == nums.length - 1) {return true;}int furthestJump = Math.min(position + nums[position], nums.length - 1);for (int nextPosition = furthestJump; nextPosition > position; nextPosition--) {if (backtrack(nums, nextPosition)) {return true;}}return false;
}}复杂度分析:
回溯算法的时间复杂度是指数级的,因为在每个位置上都会进行多次递归调用。具体来说,在最坏情况下,即每次跳跃只能跳一个格子,需要进行 n 层递归调用,每层调用需要遍历 nums 数组中的所有元素,因此总时间复杂度是 O(n^n)。
空间复杂度主要取决于递归调用栈的深度,最坏情况下,递归调用栈的深度为数组的长度,所以空间复杂度为 O(n)。
尽管回溯算法能够找到所有可能的路径,但由于其指数级的时间复杂度,对于较大的输入可能会导致超时。因此,在实际应用中,贪心算法和动态规划算法更常用和高效。
LeetCode运行结果:
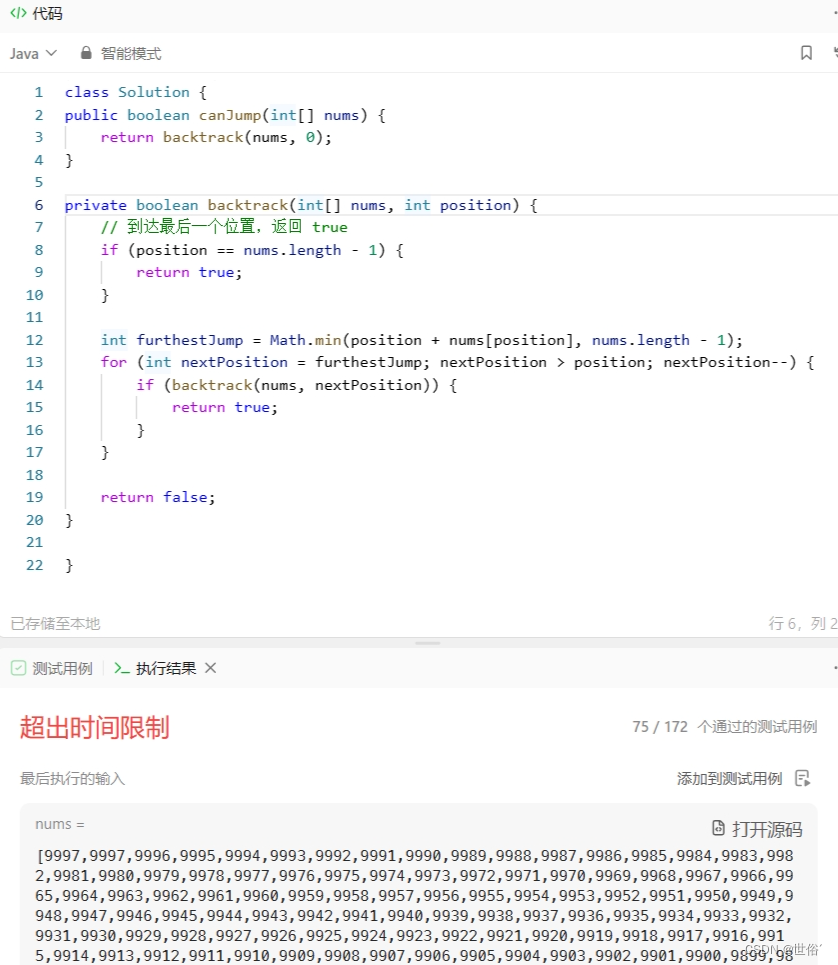
方法四:并查集
除了贪心算法、动态规划、回溯算法,还可以使用特殊的数据结构来解决跳跃游戏问题,例如并查集。
并查集是一种用于处理元素分组和查找连通性的数据结构。在跳跃游戏问题中,我们可以将每个位置看作一个节点,并按照能够跳跃到的下一个位置建立连通关系。
在实现中,我们首先定义了一个并查集类 UnionFind,其中包含 find、union 和 isConnected 等操作。在构造函数中,将每个位置初始化为其自身的根节点。
接下来,遍历数组 nums 中的每个位置,并计算出从当前位置能够跳跃到的最远位置 maxJump。然后,将当前位置与从 i+1 到 maxJump 的位置进行合并操作,表示它们之间存在连通关系。
最后,判断起点位置 0 和终点位置 n-1 是否连通,即可得出是否能够跳跃到终点位置。
class Solution {
class UnionFind {int[] parent;public UnionFind(int n) {parent = new int[n];for (int i = 0; i < n; i++) {parent[i] = i;}}public int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}public void union(int x, int y) {int rootX = find(x);int rootY = find(y);if (rootX != rootY) {parent[rootX] = rootY;}}public boolean isConnected(int x, int y) {return find(x) == find(y);}
}public boolean canJump(int[] nums) {if (nums == null || nums.length == 0) {return false;}int n = nums.length;UnionFind uf = new UnionFind(n);for (int i = 0; i < n; i++) {int maxJump = Math.min(i + nums[i], n - 1);for (int j = i + 1; j <= maxJump; j++) {uf.union(i, j);}}return uf.isConnected(0, n - 1);
}}复杂度分析:
- 时间复杂度:O(n^2),其中 n 是数组的长度。需要进行两层循环,对每个位置都进行合并操作。
- 空间复杂度:O(n),需要使用一个并查集来保存每个位置的根节点。
需要注意的是,并查集不适用于所有类型的跳跃游戏问题,只适用于某些特定情况下。在一般情况下,仍然推荐使用贪心算法、动态规划或回溯算法来解决跳跃游戏问题。
LeetCode运行结果:
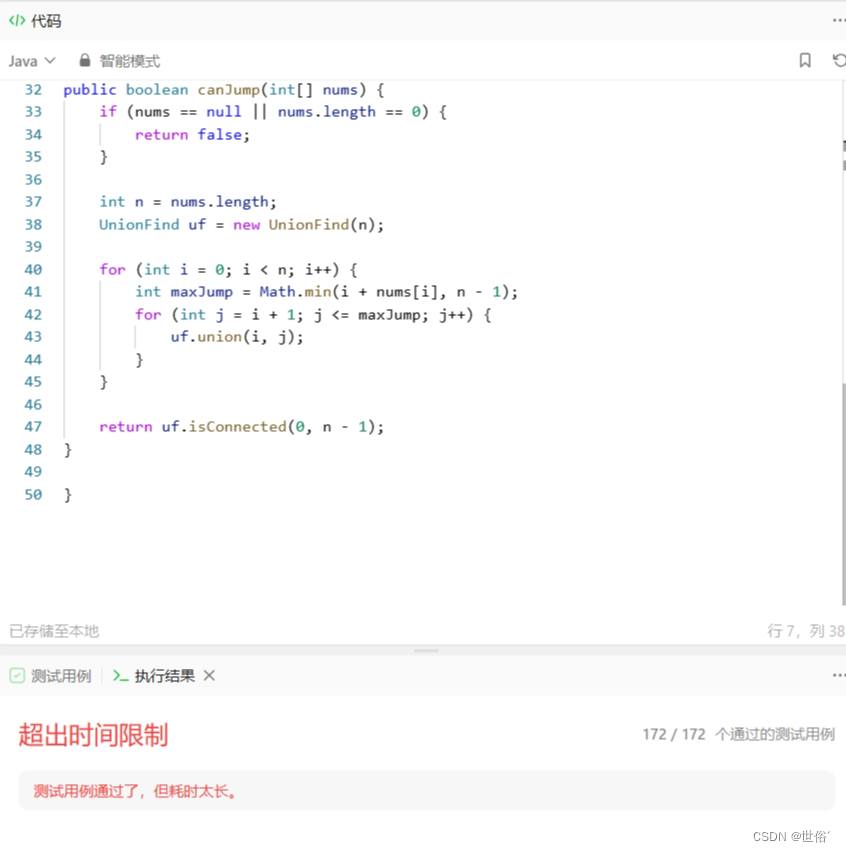
第二题
题目来源
56. 合并区间 - 力扣(LeetCode)
题目内容

解决方法
方法一:排序和遍历
这个问题可以使用排序和遍历的思路来解决。
- 首先,我们对给定的区间集合按照起始位置进行排序。这样可以确保如果有重叠的区间,它们会相邻。
- 然后,我们遍历排序后的区间集合,并维护一个当前合并区间的起始位置 start 和结束位置 end。初始时,我们将第一个区间的起始位置和结束位置分别赋值给 start 和 end。
- 接下来,我们从第二个区间开始遍历,比较当前区间的起始位置与当前合并区间的结束位置。如果当前区间的起始位置大于当前合并区间的结束位置,说明当前区间与前面的区间没有重叠,我们可以将当前合并区间 [start, end] 加入结果数组中,并更新 start 和 end 为当前区间的起始位置和结束位置。
- 否则,如果当前区间的起始位置小于等于当前合并区间的结束位置,说明当前区间与前面的区间有重叠,我们可以更新当前合并区间的结束位置为当前区间的结束位置。这样就实现了区间的合并。
- 最后,遍历完成后,将当前合并区间 [start, end] 加入结果数组中即可。
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;class Solution {public int[][] merge(int[][] intervals) {if (intervals.length <= 1) {return intervals;}// 按照区间的起始位置进行排序Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));List<int[]> merged = new ArrayList<>();int start = intervals[0][0];int end = intervals[0][1];for (int i = 1; i < intervals.length; i++) {int intervalStart = intervals[i][0];int intervalEnd = intervals[i][1];if (intervalStart <= end) {// 当前区间和前面的区间有重叠,更新当前合并区间的结束位置end = Math.max(end, intervalEnd);} else {// 当前区间和前面的区间没有重叠,将当前合并区间加入结果数组中merged.add(new int[]{start, end});// 更新当前合并区间为当前区间start = intervalStart;end = intervalEnd;}}// 将最后一个合并区间加入结果数组中merged.add(new int[]{start, end});return merged.toArray(new int[merged.size()][]);}
}
复杂度分析:
- 排序的时间复杂度为O(n log n),其中 n 是区间的数量。这是因为我们对区间进行了一次排序操作。接下来,我们遍历排序后的区间集合,每个区间只会被访问一次。因此,遍历的时间复杂度是O(n),其中 n 是区间的数量。最后,将合并后的区间转换为结果数组的过程需要O(n)的时间复杂度,其中 n 是合并后的区间数量。综上所述,算法的总时间复杂度为O(n log n) + O(n) + O(n) = O(n log n)。
- 对于空间复杂度,我们使用了一个结果集合来存储合并后的区间,其大小最多为n。因此,空间复杂度为O(n)。
注意,这里不考虑返回结果的空间复杂度。如果按照题目要求返回二维数组作为结果,该空间复杂度为O(n)。
LeetCode运行结果:
方法二:扫描线算法
除了排序和遍历的方法,还可以使用扫描线算法来合并区间。这种方法在处理区间重叠的问题时也很高效。
- 首先,我们将所有区间的起始点和结束点提取出来,并分别存储在两个数组中。对于每个点,我们还需要记录它是一个起始点还是结束点。
- 然后,我们对这些点进行排序,并使用一个变量 count 来记录当前遍历到的起始点的个数。同时,我们还需要用一个变量 start 来记录当前合并区间的起始位置。
- 接着,我们从左到右遍历这些点,并根据每个点的类型来更新 count 的值。当遇到起始点时,说明有一个新的区间开始了,因此 count 加1。当遇到结束点时,说明一个区间结束了,因此 count 减1。
- 在遍历过程中,每当 count 的值从0变为1时,说明一个新的合并区间开始了,我们将当前点的位置赋值给 start。每当 count 的值从1变为0时,说明一个合并区间结束了,我们将当前点的位置作为这个区间的结束位置,并将合并区间 [start, end] 加入结果数组中。
- 最后,我们就可以得到合并后的区间。
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;class Solution {public int[][] merge(int[][] intervals) {if (intervals.length <= 1) {return intervals;}int n = intervals.length;// 提取所有点的值和类型int[] points = new int[2 * n];int[] types = new int[2 * n];for (int i = 0; i < n; i++) {points[2 * i] = intervals[i][0];types[2 * i] = 1; // 起始点points[2 * i + 1] = intervals[i][1];types[2 * i + 1] = -1; // 结束点}// 对点进行排序Integer[] indices = new Integer[2 * n];for (int i = 0; i < 2 * n; i++) {indices[i] = i;}Arrays.sort(indices, (a, b) -> {if (points[a] != points[b]) {return Integer.compare(points[a], points[b]);}return Integer.compare(types[b], types[a]);});List<int[]> merged = new ArrayList<>();int count = 0;int start = 0;for (int index : indices) {int point = points[index];int type = types[index];if (count == 0) {start = point;}count += type;if (count == 0) {int end = point;merged.add(new int[]{start, end});}}return merged.toArray(new int[merged.size()][]);}
}
复杂度分析:
- 算法的时间复杂度为O(n log n),其中n是区间的数量。这是因为算法涉及对区间的排序操作,而排序的时间复杂度为O(n log n)。
- 算法的空间复杂度为O(n),用于存储排序后的区间和合并后的结果。
需要注意的是,在最坏情况下,即所有的区间都不重叠时,算法需要将所有区间都合并为一个大区间,此时时间复杂度为O(n)。
总之,本算法的时间复杂度和空间复杂度都是比较优秀的,是解决区间合并问题的一个非常好的算法。
LeetCode运行结果:
方法三:栈
除了排序和遍历、扫描线算法外,还有一种常见的方法是使用栈来合并区间。
具体实现思路如下:
- 首先将所有区间按照起始位置进行排序。
- 创建一个栈,将第一个区间放入栈中。
- 遍历剩余的区间,如果当前区间的起始位置大于栈顶区间的结束位置,说明两个区间不重叠,直接将当前区间入栈。 否则,将当前区间与栈顶区间合并,更新栈顶区间的结束位置为两者中的较大值。
- 遍历完所有区间后,栈中存储的就是合并后的区间。
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;class Solution {public int[][] merge(int[][] intervals) {if (intervals.length <= 1) {return intervals;}// 根据起始位置对区间进行排序Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));// 使用栈来合并区间Stack<int[]> stack = new Stack<>();stack.push(intervals[0]);for (int i = 1; i < intervals.length; i++) {int[] currentInterval = intervals[i];int[] topInterval = stack.peek();if (currentInterval[0] > topInterval[1]) {// 当前区间与栈顶区间不重叠,直接入栈stack.push(currentInterval);} else {// 合并当前区间和栈顶区间topInterval[1] = Math.max(topInterval[1], currentInterval[1]);}}// 将栈中的区间转化为数组返回List<int[]> merged = new ArrayList<>(stack);return merged.toArray(new int[merged.size()][]);}
}
复杂度分析:
使用栈的方法时间复杂度取决于排序的时间复杂度,因此为 O(n log n),其中n是区间的数量。空间复杂度为O(n),用于存储合并后的区间。
具体分析如下:
- 对区间进行排序的时间复杂度为 O(n log n),因为我们需要对所有区间按照起始位置进行排序。
- 遍历整个区间数组的时间复杂度为 O(n),因为我们只需要遍历每个区间一次,并将合并后的区间存储在一个栈中。
- 最后将栈中的元素转化为二维数组的时间复杂度为 O(n),因为我们需要遍历栈中所有元素一次,并将它们存储在一个二维数组中。
因此,总的时间复杂度为 O(n log n) + O(n) + O(n) = O(n log n)。空间复杂度为O(n),因为我们需要存储合并后的区间。
需要注意的是,排序操作是这种方法的时间复杂度瓶颈,因此如果输入区间已经有序或者近似有序,则使用这种方法可能更加高效,因为排序的时间复杂度可以达到O(n)。但是一般情况下,排序和遍历、扫描线算法仍然是解决区间合并问题的首选方法。
LeetCode运行结果:
第三题
题目来源
57. 插入区间 - 力扣(LeetCode)
题目内容


解决方法
方法一:遍历和比较
思路与算法:
-
首先,根据题目要求,我们可以将给定的区间列表按照起始端点进行排序,这样可以方便后续的处理。
-
接下来,我们需要遍历排序后的区间列表,逐个与新的区间进行比较和合并。
-
初始化一个结果列表 merged,用于存储最终的合并后的区间。
-
遍历排序后的区间列表,对于每个区间 intervals[i],与新的区间 newInterval 进行比较和合并。
-
如果 intervals[i] 的结束位置小于 newInterval 的起始位置,说明两个区间没有重叠,直接将 intervals[i] 加入 merged 中。
-
如果 intervals[i] 的起始位置大于 newInterval 的结束位置,说明后面的区间也不会有重叠,直接将 newInterval 和后面的区间加入 merged 中,并返回最终结果。
-
如果 intervals[i] 和 newInterval 存在重叠,我们需要不断地更新 newInterval 的范围,使其包括当前区间 intervals[i] 及可能的后续重叠区间,直到找到一个不与 newInterval 重叠的区间或者完成遍历。
-
-
最后,将 newInterval 添加到 merged 中,并将剩余的 intervals[i] 依次加入 merged。
-
返回 merged 列表中的区间数组作为最终结果。
import java.util.ArrayList;
import java.util.List;class Solution {public int[][] insert(int[][] intervals, int[] newInterval) {List<int[]> merged = new ArrayList<>(); // 用于存储合并后的区间int i = 0;// 将起始位置小于newInterval的区间加入结果列表while (i < intervals.length && intervals[i][1] < newInterval[0]) {merged.add(intervals[i]);i++;}// 合并与newInterval相交的区间while (i < intervals.length && intervals[i][0] <= newInterval[1]) {newInterval[0] = Math.min(newInterval[0], intervals[i][0]);newInterval[1] = Math.max(newInterval[1], intervals[i][1]);i++;}// 将合并后的newInterval加入结果列表merged.add(newInterval);// 将剩余的区间加入结果列表while (i < intervals.length) {merged.add(intervals[i]);i++;}// 将结果列表转换为数组返回return merged.toArray(new int[merged.size()][2]);}
}
复杂度分析:
- 该算法的时间复杂度为 O(n),其中 n 是区间的个数,因为需要遍历整个区间列表一次。
- 算法中使用了一个额外的空间 merged 来存储合并后的区间,空间复杂度为 O(n),其中 n 是合并后的区间的个数。
LeetCode运行结果:
相关文章:

怒刷LeetCode的第23天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:贪心算法 方法二:动态规划 方法三:回溯算法 方法四:并查集 第二题 题目来源 题目内容 解决方法 方法一:排序和遍历 方法二:扫描线算法 方法…...

Golang 中的调试技巧
掌握有效的策略和工具,实现顺畅的开发 调试是每位开发人员都必须掌握的关键技能。它是识别、隔离和解决代码库中问题的过程。在 Golang 的世界中,掌握有效的调试技巧可以显著提升您的开发工作流程,并帮助您创建更可靠和健壮的应用程序。在本…...

linux 监控内存利用率
监控内存利用率 使用free来分析CPU使用信息 #!/bin/bashDATE$(date %F" "%H:%M)IP$(ifconfig eth0 |awk -F [ :] /inet addr/{print $4}) MAIL"examplemail.com"TOTAL$(free -m |awk /Mem/{print $2})USE$(free -m |awk /Mem/{print $3-$6-$7})FREE$(($TO…...
43 验证二叉搜索树
验证二叉搜索树 理解题意:验证搜索二叉树:中序遍历是升序题解1 递归(学习学习!)题解2 中序遍历(保持升序) 给你一个二叉树的根节点 root ,判断其是否是一个 有效的二叉搜索树。 有…...
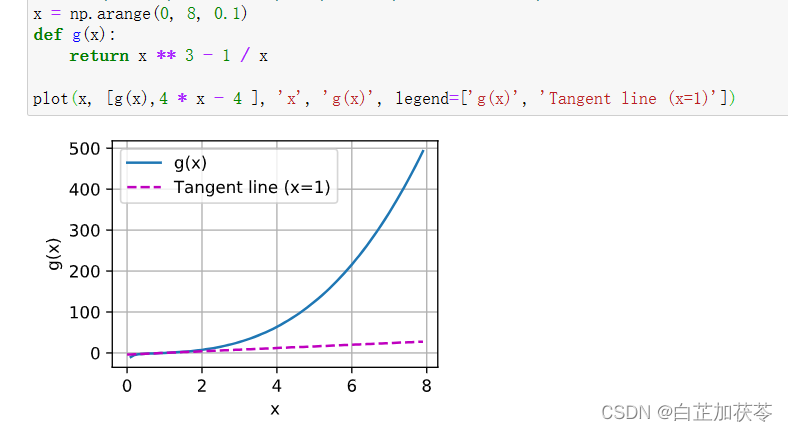
深度学习笔记之微积分及绘图
深度学习笔记之微积分及绘图 学习资料来源:微积分 %matplotlib inline from matplotlib_inline import backend_inline from mxnet import np, npx from d2l import mxnet as d2lnpx.set_np()def f(x):return 3 * x ** 2 - 4 * xdef numerical_lim(f, x, h):retur…...
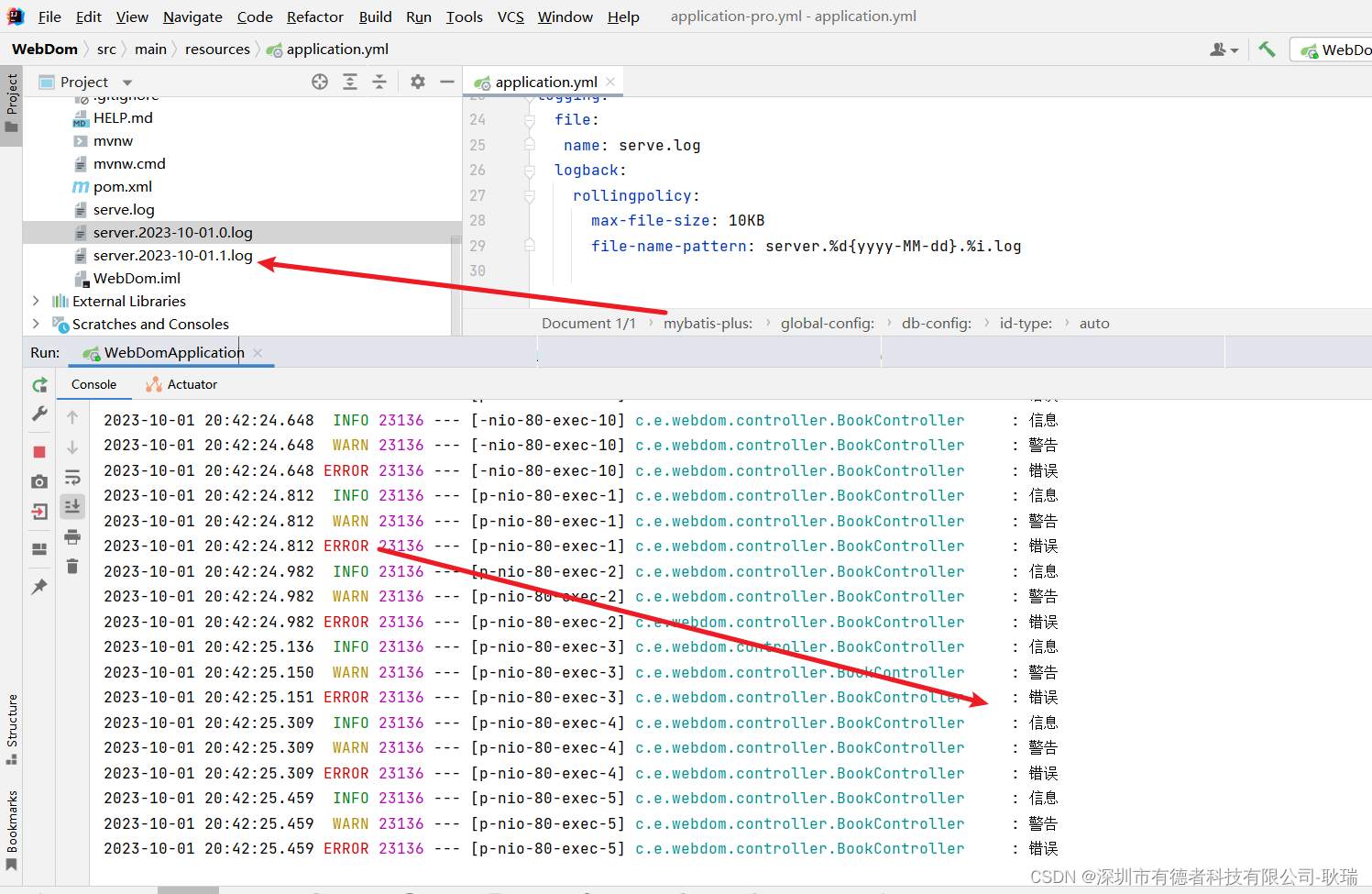
java Spring Boot按日期 限制大小分文件记录日志
上文 java Spring Boot 将日志写入文件中记录 中 我们实现另一个将控制台日志写入到 项目本地文件的效果 但是 这里有个问题 比如 我项目是个大体量的企业项目 每天会有一百万用户访问 那我每天的日志都记载同一个文件上 那不跟没记没什么区别吗? 东西怎么找&#x…...

CSS 语法
CSS 实例 CSS 规则由两个主要的部分构成:选择器,以及一条或多条声明: 选择器通常是您需要改变样式的 HTML 元素。 每条声明由一个属性和一个值组成。 属性(property)是您希望设置的样式属性(style attribute&#x…...
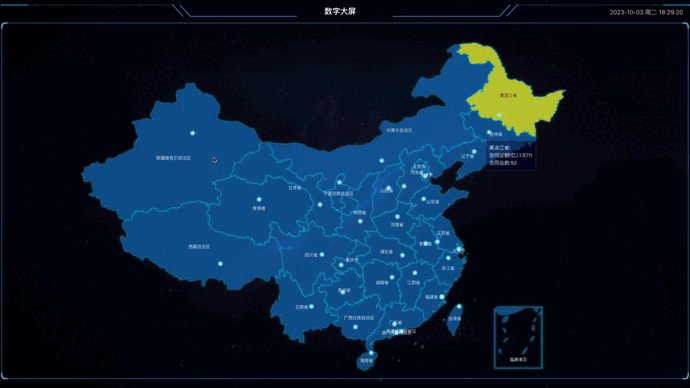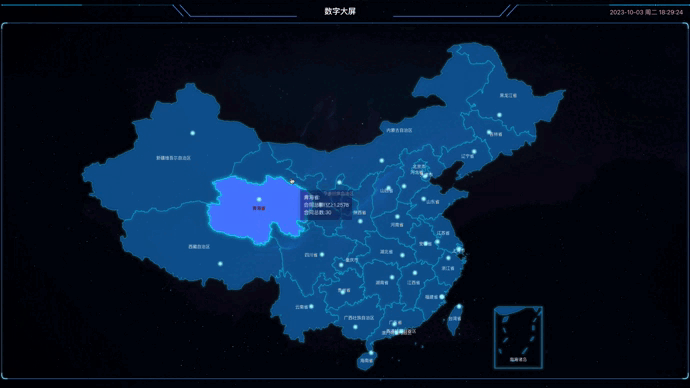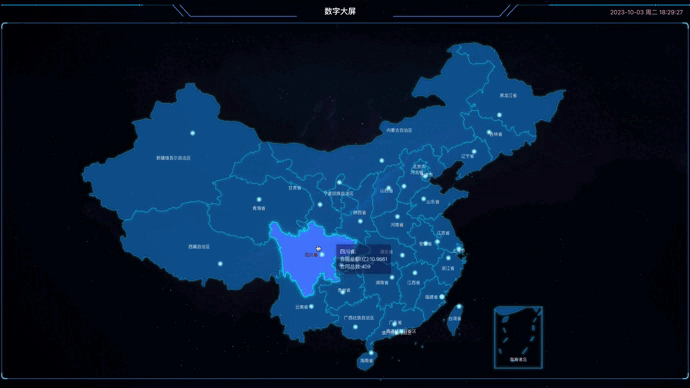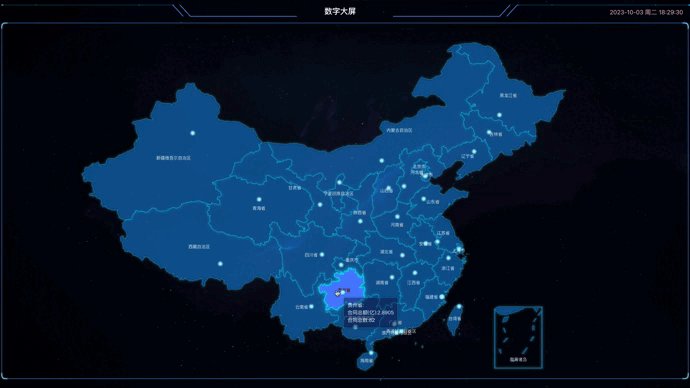
Vue3+TS+ECharts5实现中国地图数据信息显示
1.引言 最近在做一个管理系统,主要技术栈使用的是Vue3TSViteElementPlus,主要参考项目是yudao-ui-admin-vue3,其中用到ECharts5做数字大屏,展示中国地图相关信息,以此基础做一个分享,写下这篇文章。 &quo…...

PowerShell 内网不能直接安装SqlServer模块的处理办法
PowerShell 内网不能直接安装SqlServer模块的处理办法 文章目录 下载sqlserver module安装sqlserver module导入和验证sqlserver 模块推荐阅读 下载sqlserver module 首先先将sqlserver.nupkg下载到本地,我是放到了C:\windows\system32目录下。 PowerShell Galler…...

Git使用【下】
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析(3) 目录 👉🏻标签管理理解标签标签运用 …...
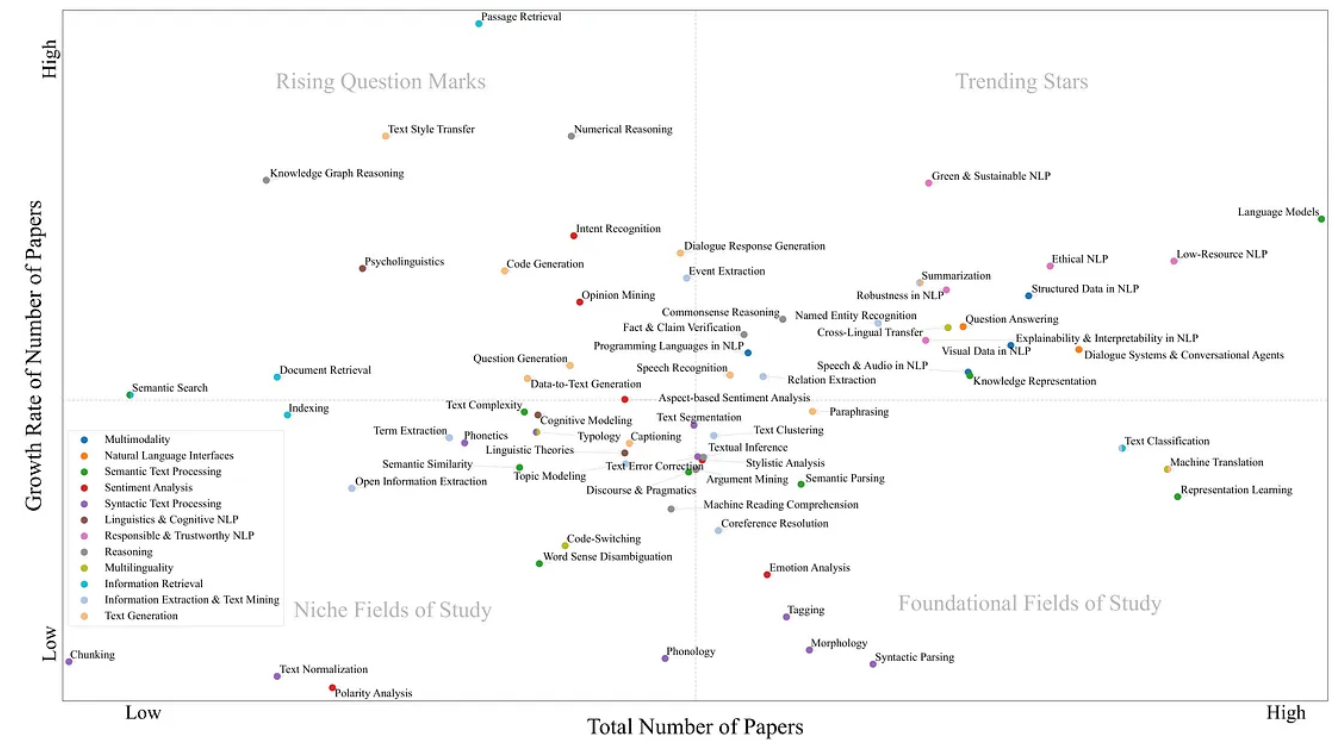
自然语言处理的分类
动动发财的小手,点个赞吧! 简介 作为理解、生成和处理自然语言文本的有效方法,自然语言处理(NLP)的研究近年来呈现出快速传播和广泛采用。鉴于 NLP 的快速发展,获得该领域的概述并对其进行维护是很困难的。…...
Flutter笔记:手写并发布一个人机滑动验证码插件
Flutter笔记 手写一个人机滑块验证码 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/133529459 写 Flut…...
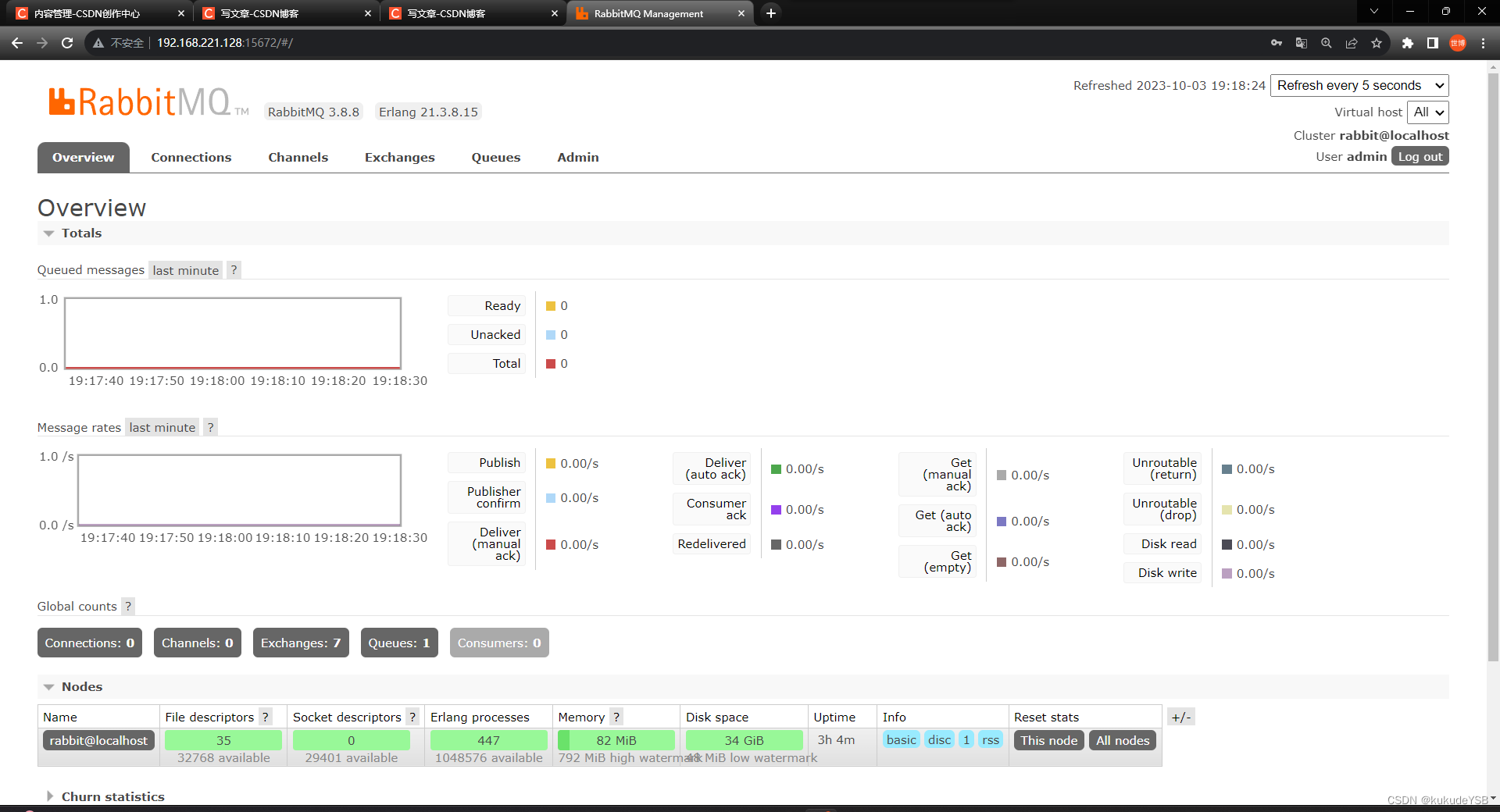
RabbitMQ安装与简单使用
安装 下载资源 可以访问官网查看下载信息rabbitmq官网 选择合适的版本,注意:rabbitmq需要下载一个Erlang才能使用 我自己是在一下两个连接中下载的 rabbitmq 3.8.8 erlang 21.3.8.15 需要下载其他版本的同学注意erlang版本是否匹配,可以访…...

不做静态化,当部署到服务器上的项目刷新出现404【已解决】
当线上项目刷新出现404页面解决方法: 在nginx配置里加入这样一段代码 try_files $uri $uri/ /index.html; 它的作用是尝试按照给定的顺序访问文件 变量解释 try_files 固定语法 $uri 指代home文件(ip地址后面的路径,假如是127.0.0.1/index/a.png&…...

SpringBoot结合Redisson实现分布式锁
🧑💻作者名称:DaenCode 🎤作者简介:啥技术都喜欢捣鼓捣鼓,喜欢分享技术、经验、生活。 😎人生感悟:尝尽人生百味,方知世间冷暖。 📖所属专栏:Sp…...

css字体属性
一、CSS字体属性用于设置文本的字体样式。以下是常用的CSS字体属性: font-family:设置文本的字体系列,可以使用多个字体,用逗号分隔。font-size:设置文本的字体大小,可用像素、百分比、em等单位。font-wei…...
云原生微服务治理 第四章 Spring Cloud Netflix 服务注册/发现组件Eureka
系列文章目录 第一章 Java线程池技术应用 第二章 CountDownLatch和Semaphone的应用 第三章 Spring Cloud 简介 第四章 Spring Cloud Netflix 之 Eureka 文章目录 系列文章目录[TOC](文章目录) 前言1、Eureka 两大组件2、Eureka 服务注册与发现3、案例3.1、创建主工程3.1.1、主…...
】)
【白细胞介素6(IL-6)】
## IL-6,至关重要的多功能细胞因子 ## 聊一聊白细胞介素6(IL-6) ## 简述:国内外IL-6 _ IL-6R在研药物一览_药智新闻.2017 ## 研究项目|靶向IL-6药物在研现状 2021...

设计模式之抽象工厂模式--创建一系列相关对象的艺术(简单工厂、工厂方法、到抽象工厂的进化过程,类图NS图)
目录 概述概念适用场景结构类图 衍化过程业务需求基本的数据访问程序工厂方法实现数据访问程序抽象工厂实现数据访问程序简单工厂改进抽象工厂使用反射抽象工厂反射配置文件衍化过程总结 常见问题总结 概述 概念 抽象工厂模式是一种创建型设计模式,它提供了一种将相…...
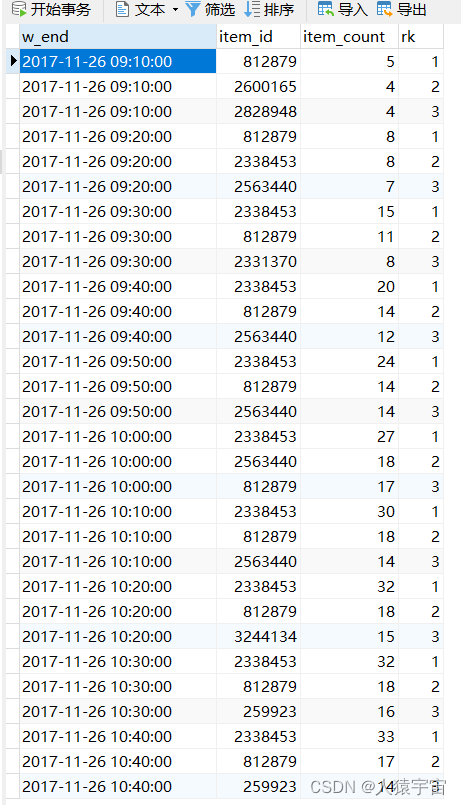
大数据-玩转数据-Flink SQL编程实战 (热门商品TOP N)
一、需求描述 每隔30min 统计最近 1hour的热门商品 top3, 并把统计的结果写入到mysql中。 二、需求分析 1.统计每个商品的点击量, 开窗2.分组窗口分组3.over窗口 三、需求实现 3.1、创建数据源示例 input/UserBehavior.csv 543462,1715,1464116,pv,1511658000 662867,22…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
