(粗糙的笔记)动态规划
动态规划算法框架:
- 问题结构分析
- 递推关系建立
- 自底向上计算
- 最优方案追踪
背包问题
输入:
- n n n个商品组成的集合 O O O,每个商品有两个属性 v i v_i vi和 p i p_i pi,分别表示体积和价格
- 背包容量 C C C
输出:
- 求解一个商品子集 S ⊆ O S\subseteq O S⊆O
直观策略
- 策略1:按商品价格由高到低排序,优先挑选价格高的商品
- 策略2:按商品体积由小到大排序,优先挑选体积小的商品
- 策略3:按商品价值与体积的比由高到低排序,优先挑选比值高的商品
这三种策略都不能保证得到最优解
蛮力枚举
- 枚举所有商品组合: 2 n − 1 2^n-1 2n−1种情况
- 检查体积约束
递归函数KnapsackSR(h,i,c):
- 在第 h h h个到第 i i i个商品中,容量为 c c c时最优解
- 选择啤酒: K n a p s a c k S R ( 1 , 4 , 3 ) + 24 KnapsackSR(1,4,3)+24 KnapsackSR(1,4,3)+24
- 不选啤酒: K n a p s a c k S R ( 1 , 4 , 13 ) KnapsackSR(1,4,13) KnapsackSR(1,4,13)
伪代码:
输入:商品集合{h,...,i},背包容量c
输出:最大总价格P
if c<0 then
| return 0
end
if i <= h-1 then
| return 0
end
P1 <- KnapsackSR(h,i-1,c-vi)
P2 <- KnapsackSR(h,i-1,c)
P <- max(P1+pi,P2)
return P
重复求解大量子问题: O ( 2 n ) O(2^n) O(2n)
动态规划
从蛮力枚举到带备忘递归
- 优化子问题解,避免重复计算
构造备忘录P[i,c],P[i,c]表示在前i个商品中选择,背包容量为c时的最优解
输入:商品集合{h,...,i},背包容量c
输出:最大总价格P
if c<0 then
| return 0
end
if i <= h-1 then
| return 0
end
if P[i,c]!=NULL then
| return P[i,c]
end
P1 <- KnapsackMR(h,i-1,c-vi)
P2 <- KnapsackMR(h,i-1,c)
P[i,c] <- max(P1+pi,P2)
return P[i,c]
递推求解
容量为0时: P [ i , 0 ] = 0 P[i,0]=0 P[i,0]=0
没有商品时: P [ 0 , c ] = 0 P[0,c]=0 P[0,c]=0
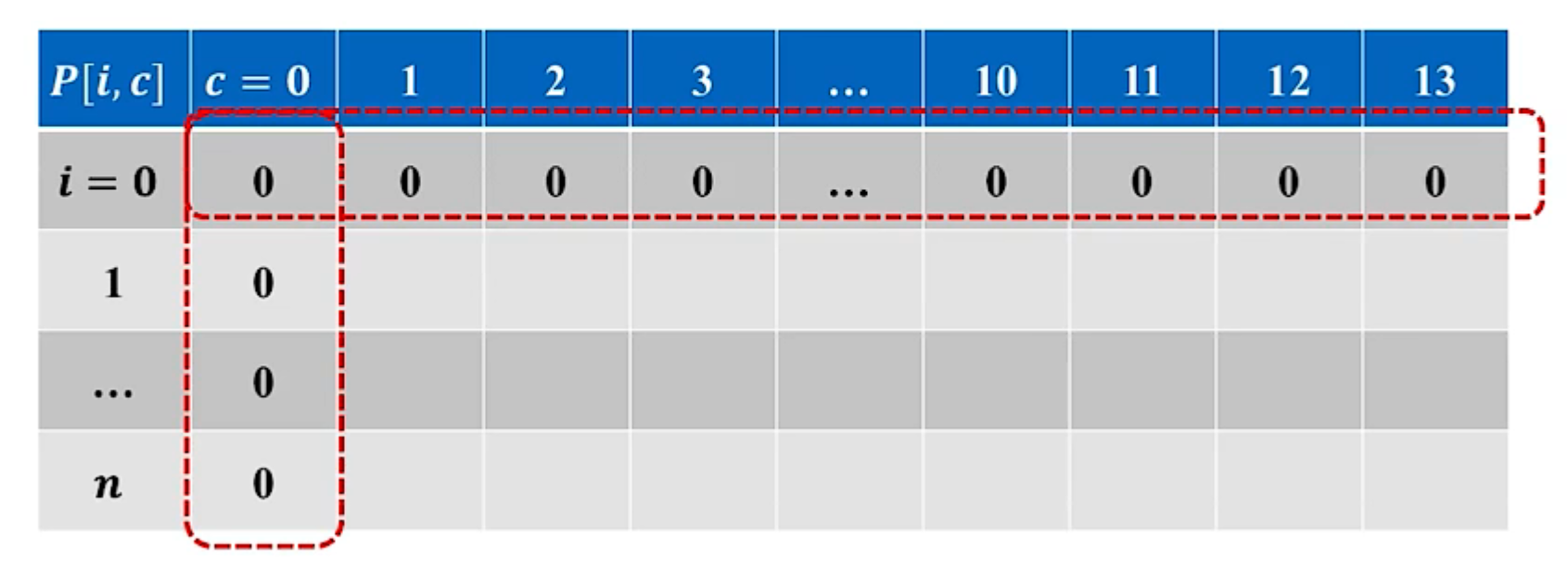
确定计算顺序:
- 按从左往右、从上到下的顺序计算
问题:如何确定选取了哪些商品
- 记录决策过程:KaTeX parse error: {align} can be used only in display mode.
回溯解决方案:
- 倒序判断是否选择商品
- 根据选择结果,确定最优子问题
伪代码:
输入:商品集合{h,...,i},背包容量c
输出:最大总价格P
//初始化,创建二维数组P和Rec
for i <- 0 to C do
| P[0,i] <- 0
end
for i <- 0 to n do
| P[i,0] <- 0
end
//求解表格
for i <- 1 to n do
| for c <- 1 to C do
| | if v[i]<=c and p[i]+P[i-1,c-v[i]]>P[i-1,c] then
| | | P[i,c]=p[i]+P[i-1,c-v[i]]
| | | Rec[i,c] <- 1
| | end
| | else
| | | P[i,c] <- P[i-1,c]
| | | Rec[i,c] <- 0
| | end
| end
end
时间复杂度: O ( n ⋅ C ) O(n\cdot C) O(n⋅C)
上面带备忘递归和递推求解的方法都属于动态规划:
- 带备忘递归:自顶向下
- 递推求解:自底向上
最优子结构性质:
- 问题的最优解由相关子问题最优解组合而成
- 子问题可以独立求解
动态规划与分而治之的区别:
- 动态规划:重叠子问题
- 分而治之:独立子问题
最大子数组
问题结构分析:
- 给出问题表示: D [ i ] D[i] D[i]为以 X [ i ] X[i] X[i]开头的最大子数组和
- 明确原始问题 S m a x = m a x { D i } S_{max}=max\{D_i\} Smax=max{Di}
递推关系建立:
- 情况一: D [ i + 1 ] > 0 D[i+1]>0 D[i+1]>0,则 D [ i ] = X [ i ] + D [ i + 1 ] D[i]=X[i]+D[i+1] D[i]=X[i]+D[i+1]
- 情况二: D [ i + 1 ] ≤ 0 D[i+1]\leq0 D[i+1]≤0,则 D [ i ] = X [ i ] D[i]=X[i] D[i]=X[i]
自底向上计算:
- 初始化: D [ n ] = X [ n ] D[n]=X[n] D[n]=X[n]
- 递推公式:KaTeX parse error: {align} can be used only in display mode.
记录决策过程:
- 构造追踪数组 R e c [ 1.. n ] Rec[1..n] Rec[1..n]
- 情况一:结尾相同,则 R e c [ i ] = R e c [ i + 1 ] Rec[i]=Rec[i+1] Rec[i]=Rec[i+1]
- 情况二:结尾不同,则 R e c [ i ] = i Rec[i]=i Rec[i]=i
最优方案追踪:
- 从子问题中查找最优解
- 最大子数组开头位置: i i i
- 最大子数组结尾位置: R e c [ i ] Rec[i] Rec[i]
伪代码:
输入:数组X,数组长度n
输出:最大子数组和Smax,子数组起止位置l,r
//初始化
D[n] <- X[n]
Rec[n] <- n
//动态规划
for i <- n-1 to 1 do
| if D[i+1]>0 then
| | D[i] <- X[i]+D[i+1]
| | Rec[i] <- Rec[i+1]
| end
| else
| | D[i] <- X[i]
| | Rec[i] <-i
| end
end
//查找解
Smax <- D[1]
for i <- 2 to n do
| if Smax<D[i] then
| | Smax<-D[i]
| | l <- i
| | r <- Rec[i]
| end
end
return Smax,l,r
最长公共子序列
子序列:将给定序列中零个或多个元素去掉后所得的结果
蛮力枚举
枚举所有子序列
可能存在最优子结构和重叠子问题
动态规划
问题结构分析:
- 给出问题表示: C [ i , j ] C[i,j] C[i,j]表示 X [ 1.. i ] X[1..i] X[1..i]和 Y [ 1.. j ] Y[1..j] Y[1..j]的最长公共子序列长度
递推关系建立:分析最优子结构
- 考察末尾字符:
- 情况1: x i ≠ y j x_i\neq y_j xi=yj时, C [ i , j ] = m a x { C [ i , j − 1 ] , C [ i − 1 , j ] } C[i,j]=max\{ C[i,j-1],C[i-1,j] \} C[i,j]=max{C[i,j−1],C[i−1,j]}
- 情况2: x i = y j x_i= y_j xi=yj时, C [ i , j ] = C [ i − 1 , j − 1 ] + 1 C[i,j]= C[i-1,j-1]+1 C[i,j]=C[i−1,j−1]+1
自底向上计算:确定计算顺序
- 初始化: C [ i , 0 ] = C [ 0. j ] = 0 C[i,0]=C[0.j]=0 C[i,0]=C[0.j]=0//某序列长度为0时,最长公共子序列长度为0
- 递推公式:KaTeX parse error: {align} can be used only in display mode.
最优方案追踪:记录决策过程
- 构造追踪数组 r e c [ 1.. n ] rec[1..n] rec[1..n],记录子问题来源:KaTeX parse error: {align} can be used only in display mode.
伪代码:
输入:两个序列X,Y
输出:X和Y的最长公共子序列
n <- length(X)
m <- length(Y)
//初始化
新建二维数组C[n,m]和rec[n,m]
for i <- 0 to n do
| C[i,0] <-0
end
for j <- 0 to m do
| C[0,j] <- 0
end
//动态规划
for i <- 1 to n do
| for j <- 1 to m do
| | if Xi=Yj then
| | | C[i,j] <- C[i-1.j-1]+1
| | | rec[i,j] <- 'LU'
| | end
| | else if C[i-1,j]>=C[i,j-1] then
| | | C[i,j] <- C[i-1,j]
| | | rec[i,j] <- 'U'
| | end
| | else
| | | C[i,j] <- C[i,j-1]
| | | rec[i,j] <- 'L'
| | end
| end
end
return C,rec
时间复杂度: O ( n ⋅ m ) O(n\cdot m) O(n⋅m)
最长公共子串
子串:给定序列中零个或多个连续的元素组成的子序列
蛮力枚举
- 序列X和序列Y各选择一个位置
- 依次检查元素是否匹配:
- 元素相等则继续匹配
- 元素不等或某序列已达端点,匹配终止
可能存在最优子结构和重叠子问题。
动态规划
问题结构分析:
- 给出问题表示: C [ i , j ] C[i,j] C[i,j]表示 X [ 1.. i ] X[1..i] X[1..i]和 Y [ 1.. j ] Y[1..j] Y[1..j]中,以 x i x_i xi和 y j y_j yj结尾的最长公共子串 Z [ 1.. l ] Z[1..l] Z[1..l]的长度
递推关系建立:分析最优子结构
- KaTeX parse error: {align} can be used only in display mode.
自底向上计算:确定计算顺序
- 初始化: C [ i , 0 ] = C [ 0. j ] = 0 C[i,0]=C[0.j]=0 C[i,0]=C[0.j]=0//某序列长度为0时,最长公共子串长度为0
- 原始问题: p m a x = m a x { C [ i , j ] } p_{max}=max\{C[i,j]\} pmax=max{C[i,j]}
最优方案追踪:记录决策过程
- 最长公共子串末尾位置 p m a x p_{max} pmax
- 最长公共子串长度 l m a x l_{max} lmax
伪代码
输入:两个字符串X,Y
输出:X和Y的最长公共子串
//初始化
n <- length(X)
m <- length(Y)
新建二维数组C[n,m]
lmax <- 0
pmax <- 0
for i <- 0 to n do
| C[i,0] <- 0
end
for j <- 0 to n do
| C[0,j] <-0
end
//动态规划
for i <- 1 to n do
| for j <- 1 to m do
| | if Xi != Yj then
| | | C[i,j] <- 0
| | end
| | else
| | | C[i,j] <- C[i-1,j-1]+1
| | | if C[i,j] > lmax then
| | | | lmax <- C[i,j]
| | | | pmax <- i
| | | end
| | end
| end
end编辑距离问题
编辑操作:删除、插入、替换
递推关系建立:只操作 s s s串
- 删除: D [ i , j ] = D [ i − 1 , j ] + 1 D[i,j]=D[i-1,j]+1 D[i,j]=D[i−1,j]+1
- 插入: D [ i , j ] = D [ i , j − 1 ] + 1 D[i,j]=D[i,j-1]+1 D[i,j]=D[i,j−1]+1
- 替换:KaTeX parse error: {align} can be used only in display mode.
- 综合以上三种方式:KaTeX parse error: {align} can be used only in display mode.
- 最小编辑距离VS最长公共子序列:
- KaTeX parse error: {align} can be used only in display mode.
- KaTeX parse error: {align} can be used only in display mode.
自底向上计算:
- 初始化:
- D [ i , 0 ] = i D[i,0]=i D[i,0]=i//把长度为 i i i的串变为空串至少需要 i i i次删除操作
- D [ j , 0 ] = j D[j,0]=j D[j,0]=j//把空串变为长度为 j j j的串至少需要 j j j次插入操作
- 递推公式:
- KaTeX parse error: {align} can be used only in display mode.
最优方案追踪:
- 追踪数组 R e c Rec Rec,记录子问题来源
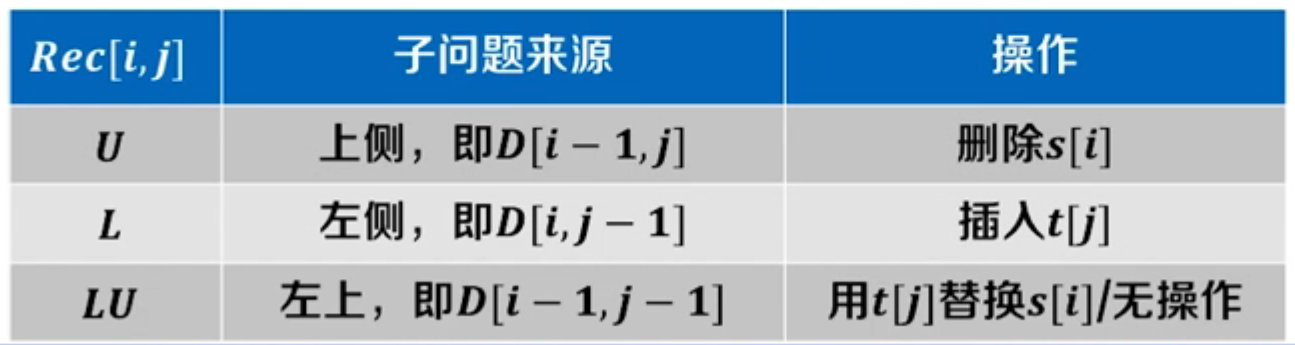
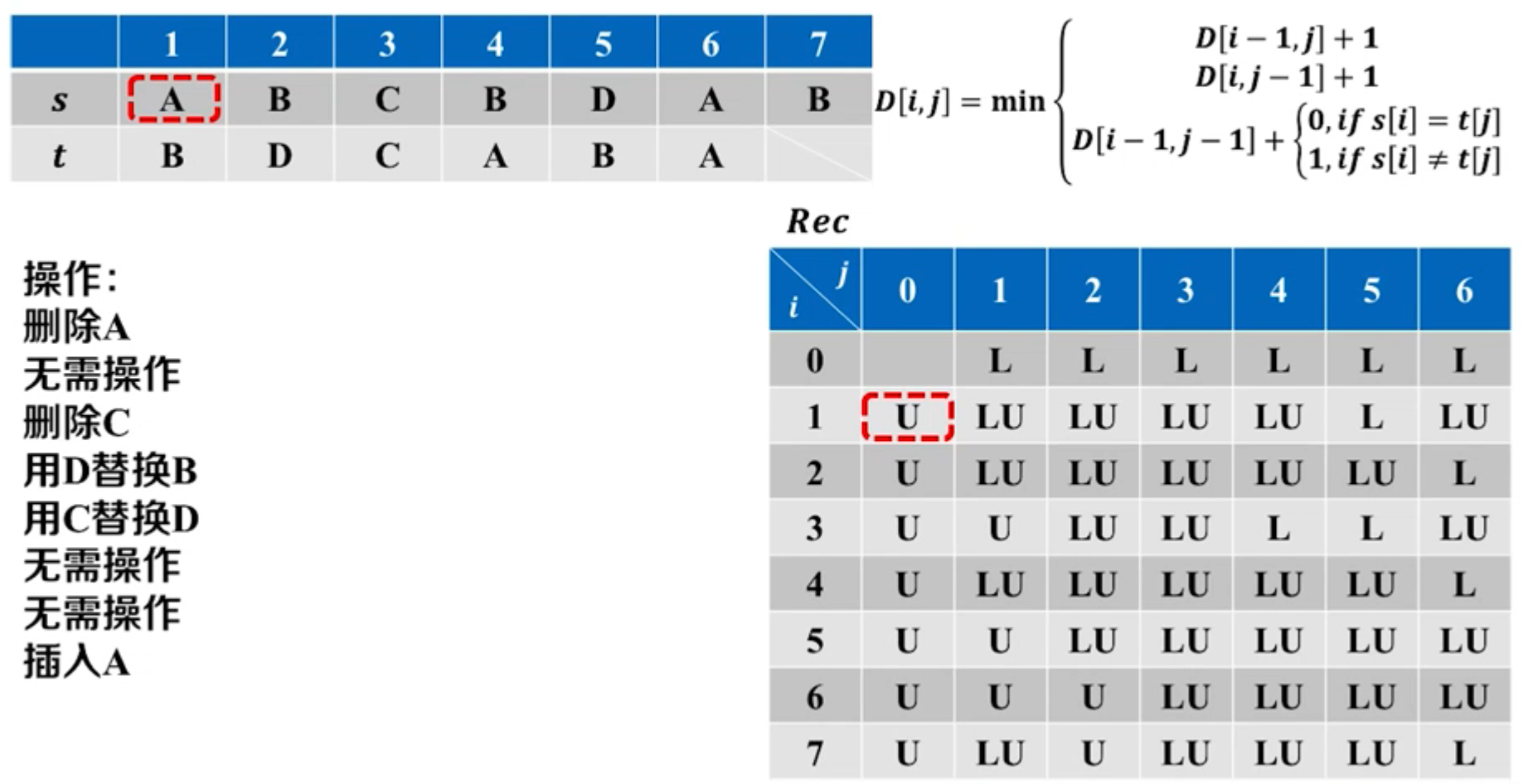
伪代码
输入:字符串s和t
输出:s和t的最小编辑距离
n <- length(s)
m <- length(t)
新建D[0..n,0..m],Rec[0..n,0..m]两个数组
//初始化
for i <- 0 to n do
| D[i,0] <- i
| Rec[i,0] <- 'U'
end
for j <- 0 to m do
| D[0,j] <- j
| Rec[0,j] <- 'L'
end
//动态规划
for i <- 1 to n do
| for j <- 1 to m do
| | c <- 0
| | if si!=tj then
| | | c <- 1
| | end
| | replace <- D[i-1,j-1]+c
| | delete <- D[i-1,j]+1
| | insert <- D[i,j-1]+1
| | if replace =min{replace,delete,insert} then
| | | D[i,j] <- D[i-1,j-1]+c
| | | Rec[i,j] <- 'LU'
| | end
| | else if insert = min{replace,delete,insert} then
| | | D[i,j] <- D[i,j-1]+1
| | | Rec[i,j] <- 'L'
| | end
| | else
| | | D[i,j] <- D[i-1,j]+1
| | | Rec[i,j] <- 'U'
| | end
| end
end
最优方案追踪-伪代码
输入:矩阵Rec,字符串s,t,索引位置i,j
输出:操作序列
if i=0 and j=0 then
| return NULL
end
if Rec[i,j]='LU' then
| Print-MED(Rec,s,t,i-1,j-1)
| if si=tj then
| | print '无需操作'
| end
| else
| | print '用tj代替si'
| end
end
else if Rec[i,j]='U' then
| Print-MED(Rec,s,t,i-1,j)
| print '删除si'
end
else
| Print-MED(Rec,s,t,i,j-1)
| print '插入tj'
end
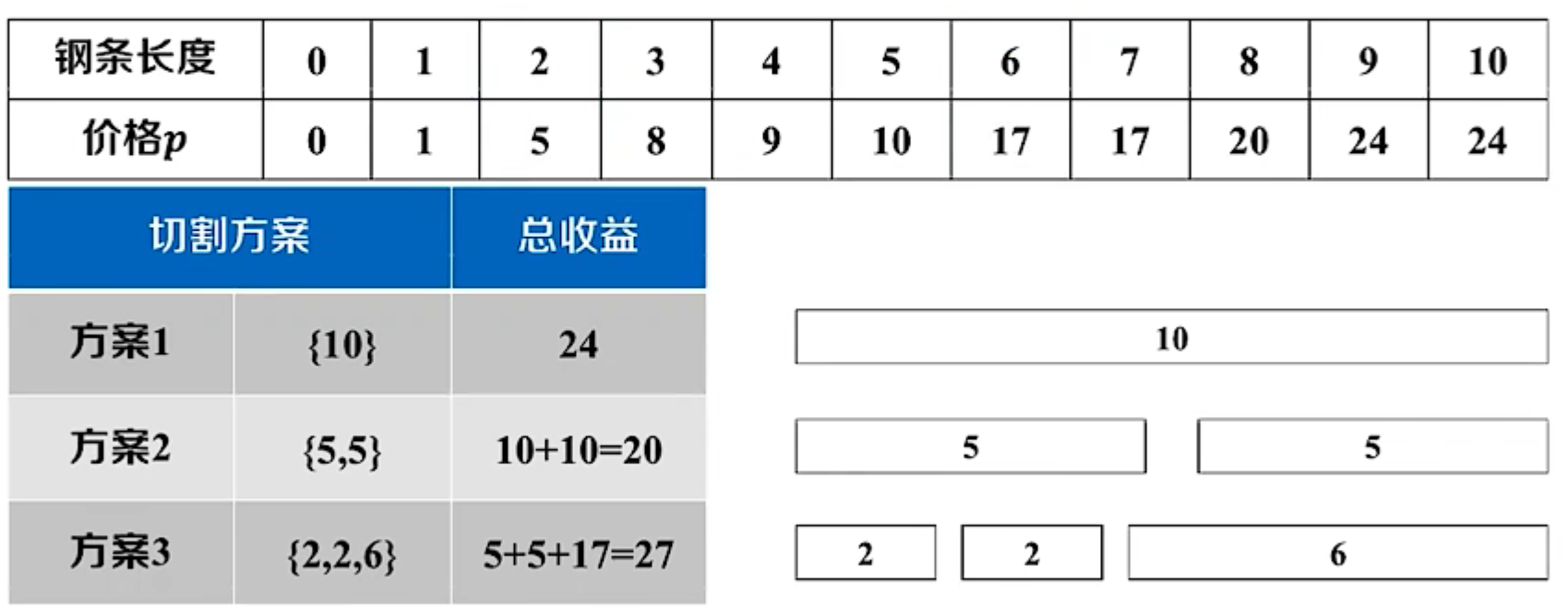
钢条切割问题
形式化定义
输入:
- 钢条长度 n n n
- 价格表 p l p_l pl:表示长度为 l l l的钢条价格
输出:
- 一组切割方案,令收益最大
问题简化
假设至多切割1次,枚举所有可能的切割位置:
- 不切: p [ 10 ] p[10] p[10]
- 切割: p [ i ] + p [ 10 − i ] p[i]+p[10-i] p[i]+p[10−i]
假设至多切割2次:
- 先将钢条切割一段
- 在剩余钢条中继续切割,剩余的问题变为至多切一刀的问题
原始问题不限制切割次数
- 可能存在最优子结构和重叠子问题
动态规划
问题结构分析:
- 给出问题表示: C [ j ] C[j] C[j]表示切割长度为 j j j的钢条可得的最大收益
递推关系建立: C [ j ] = m a x { p [ i ] + C [ j − i ] , p [ j ] } C[j]=max\{ p[i]+C[j-i],p[j] \} C[j]=max{p[i]+C[j−i],p[j]}
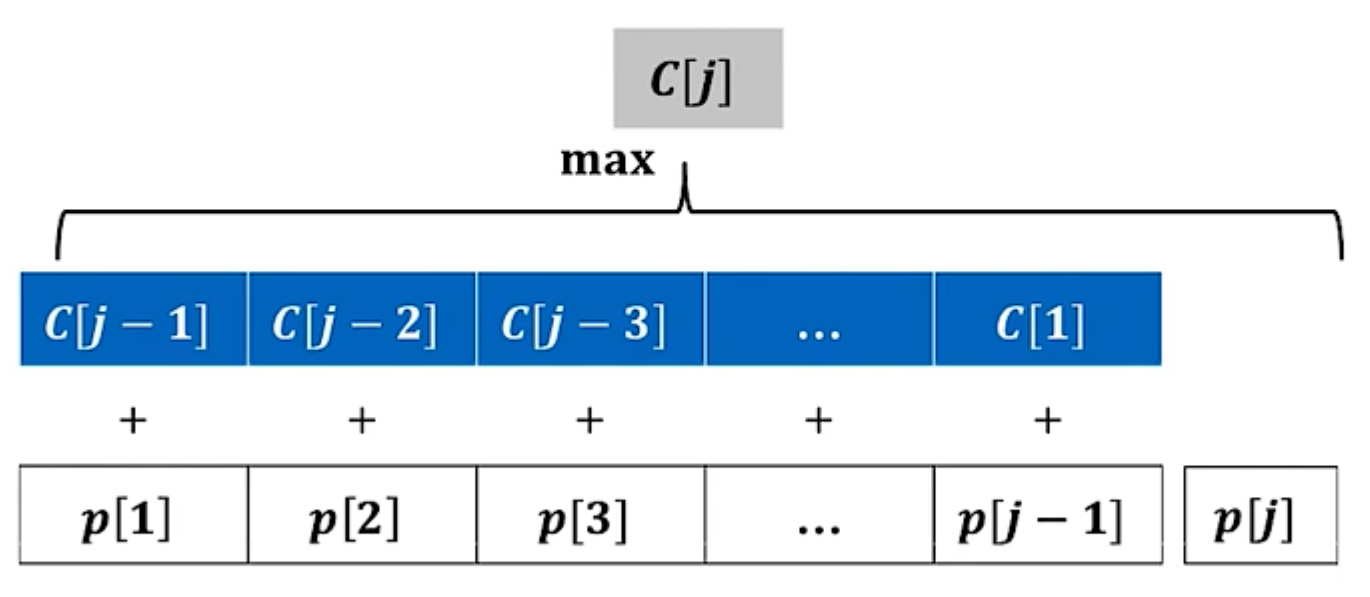
自底向上计算:
- 初始化: C [ 0 ] = 0 C[0]=0 C[0]=0//切割长度为0的钢条,总收益为0
- 递推公式: C [ j ] = m a x { p [ i ] + C [ j − i ] , p [ j ] } C[j]=max\{ p[i]+C[j-i],p[j] \} C[j]=max{p[i]+C[j−i],p[j]}
最优方案追踪:记录决策过程
- 构造追踪数组 r e c [ 1.. n ] rec[1..n] rec[1..n]
- r e c [ j ] rec[j] rec[j]:记录长度为 j j j的钢条的最优切割方案
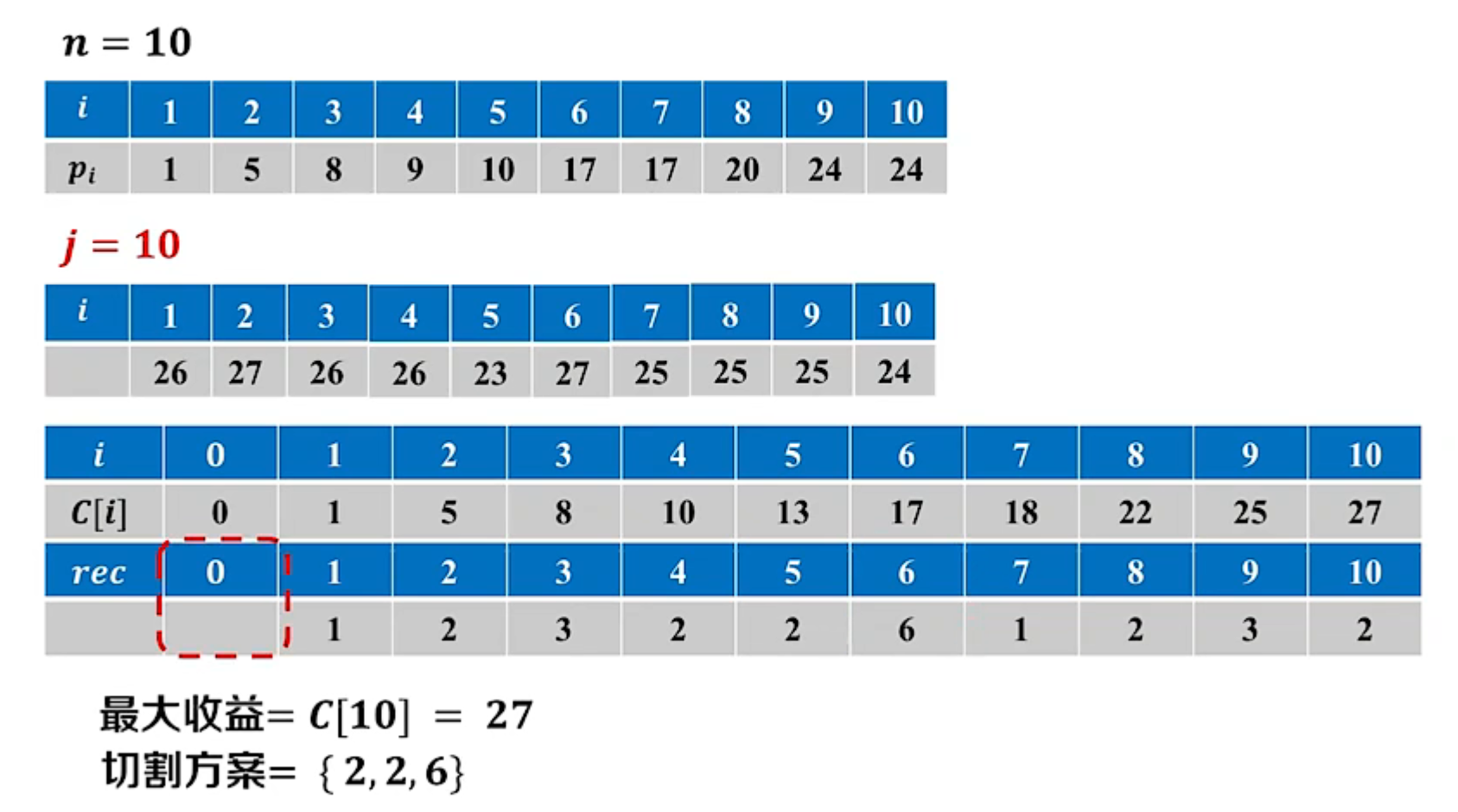
伪代码
输入:钢条价格表p[1..n],钢条长度n
输出:最大收益C[n],钢条切割方案
//初始化
新建一维数组C[0..n],rec[0..n]
C[0] <- 0
//动态规划
for j <- 1 to n do
| q <- p[j]
| rec[j] <- j
| for i <- 1 to j-1 do
| | if q<p[i]+C[j-i] then
| | | q <- p[i]+C[j-i]
| | | rec[j] <- i
| | end
| end
| C[j] <- q
end
//输出最优方案
while n>0 do
| print rec[n]
| n <- n-rec[n]
end
时间复杂度为 O ( n 2 ) O(n^2) O(n2)
矩阵链乘法问题
矩阵乘法时间复杂度:
- 计算一个数字: q q q次标量乘法
- 共 p × r p\times r p×r个数字: Θ ( p q r ) \Theta(pqr) Θ(pqr)
三个矩阵相乘:
- ( U V ) W = U ( V W ) (UV)W=U(VW) (UV)W=U(VW)
- 新问题:矩阵乘法结合的顺序

n n n个矩阵相乘:
- 一系列矩阵按顺序排列
- 每个矩阵的行数=前一个矩阵的列数
- n n n个矩阵相乘也被称为矩阵链乘法
问题定义
输入:
- n n n个矩阵组成的矩阵链 U 1.. n = < U 1 , U 2 , . . . , U n > U_{1..n}=<U_1,U_2,...,U_n> U1..n=<U1,U2,...,Un>
- 矩阵链 U 1.. n U_{1..n} U1..n对应的维度数分别为 p 0 , p 1 , . . . , p n p_0,p_1,...,p_n p0,p1,...,pn, U i U_i Ui的维度是 p i − 1 × p i p_{i-1}\times p_i pi−1×pi
输出:
- 找到一种加括号的方式,使得矩阵链标量乘法的次数最少
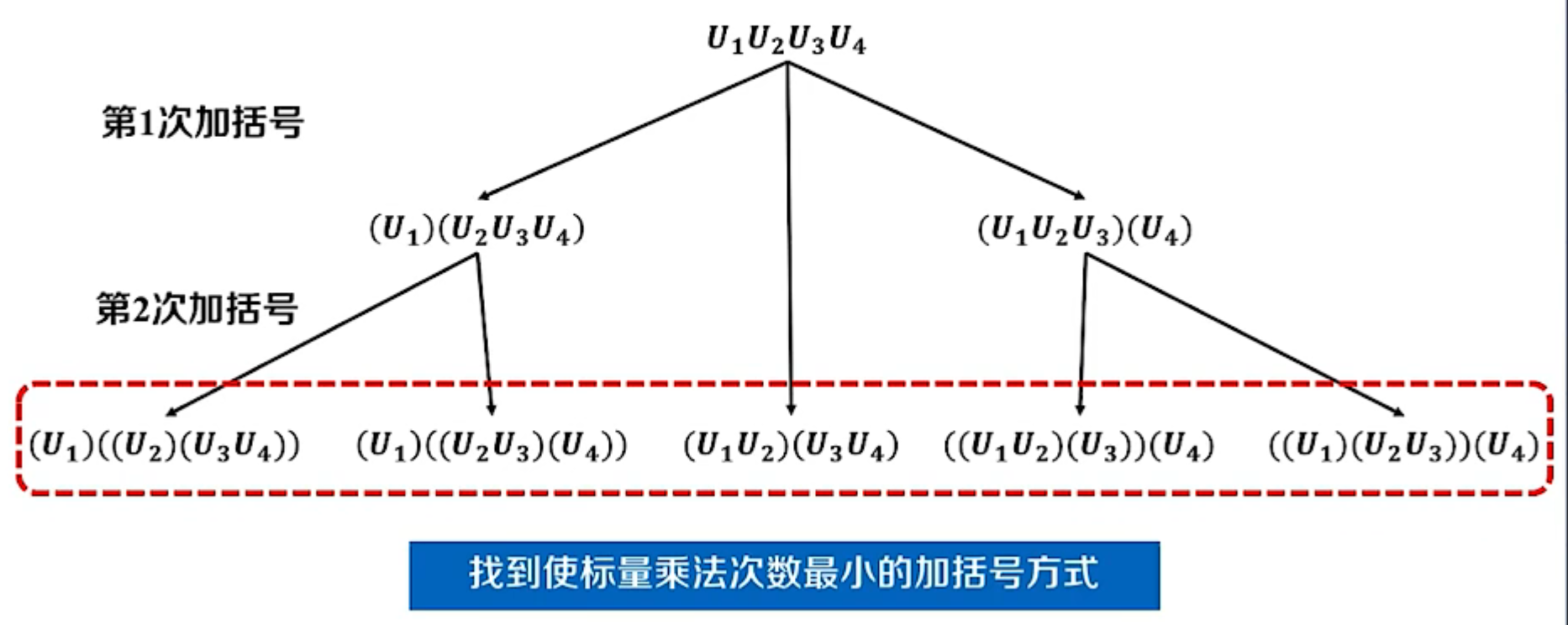
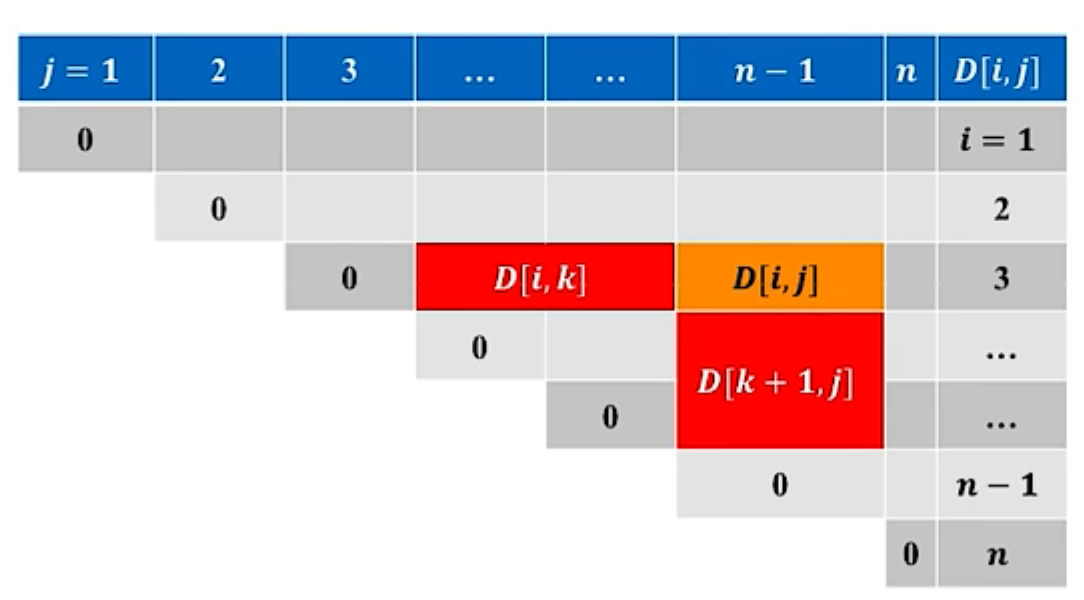
如何保证不遗漏最优分割位置:
- 枚举所有可能位置 i . . j − 1 i..j-1 i..j−1,共 j − i j-i j−i种
问题结构分析:
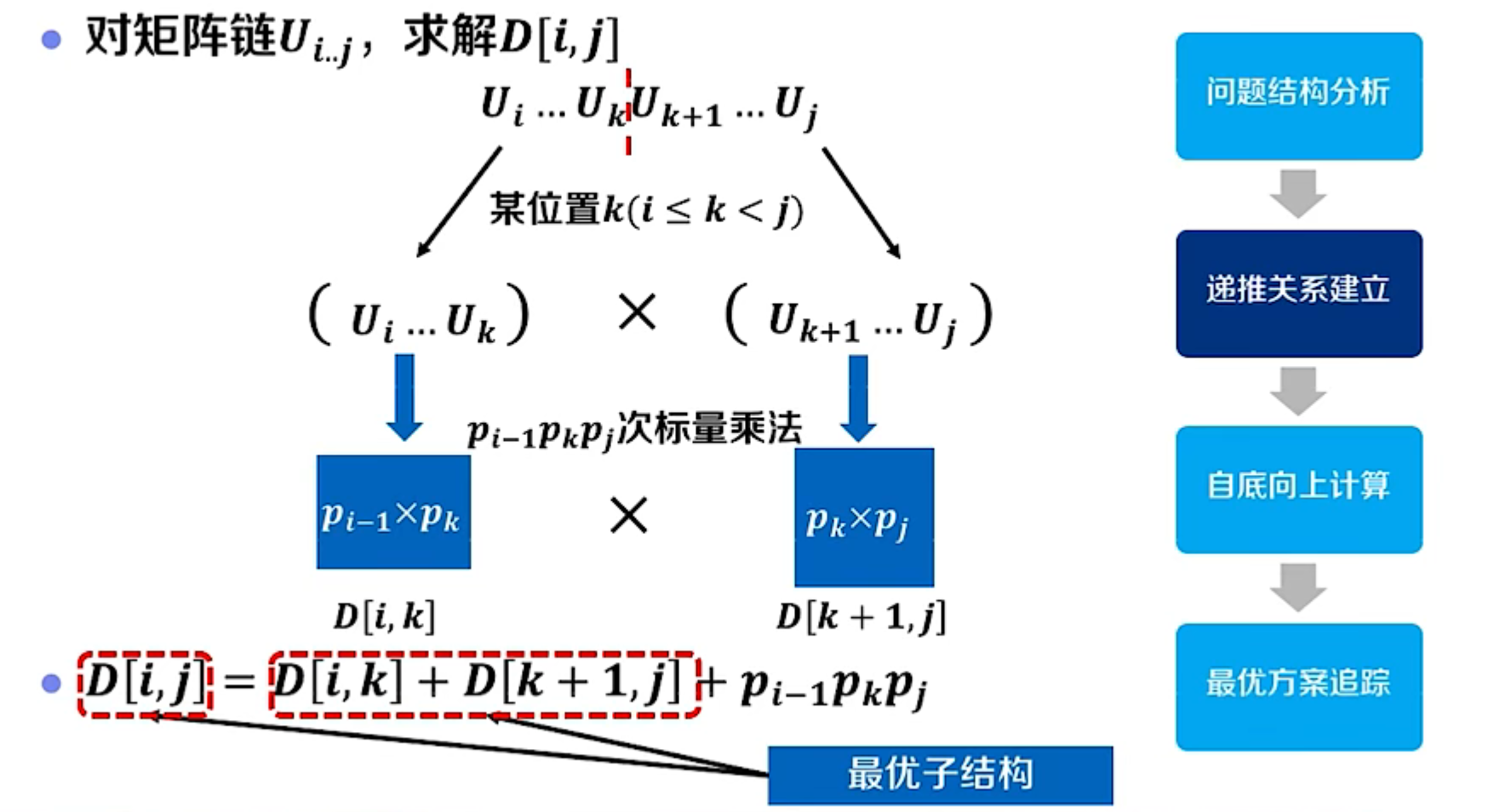
- 明确原始问题: D [ 1 , n ] D[1,n] D[1,n]表示计算矩阵链 U 1.. n U_{1..n} U1..n所需标量乘法的最小次数
递推关系建立:
- 对每个位置 k ( i ≤ k ≤ j ) k(i\leq k\leq j) k(i≤k≤j): D [ i , j ] = D [ i , k ] + D [ k + 1 , j ] + p i − 1 p k p j D[i,j]=D[i,k]+D[k+1,j]+p_{i-1}p_kp_j D[i,j]=D[i,k]+D[k+1,j]+pi−1pkpj
- 枚举所有 k k k,得到递推式: D [ i , j ] = m i n ( D [ i , k ] + D [ k + 1 , j ] + p i − 1 p k p j ) D[i,j]=min(D[i,k]+D[k+1,j]+p_{i-1}p_kp_j) D[i,j]=min(D[i,k]+D[k+1,j]+pi−1pkpj)
自底向上计算:
- 初始化: i = j i=j i=j时,矩阵链只有一个矩阵,乘法次数为
0。
最优方案追踪:
- 构造追踪数组 R e c [ 1.. n , 1.. n ] Rec[1..n,1..n] Rec[1..n,1..n]
- R e c [ i , j ] Rec[i,j] Rec[i,j]:矩阵链 U i . . j U_{i..j} Ui..j的最优分割位置
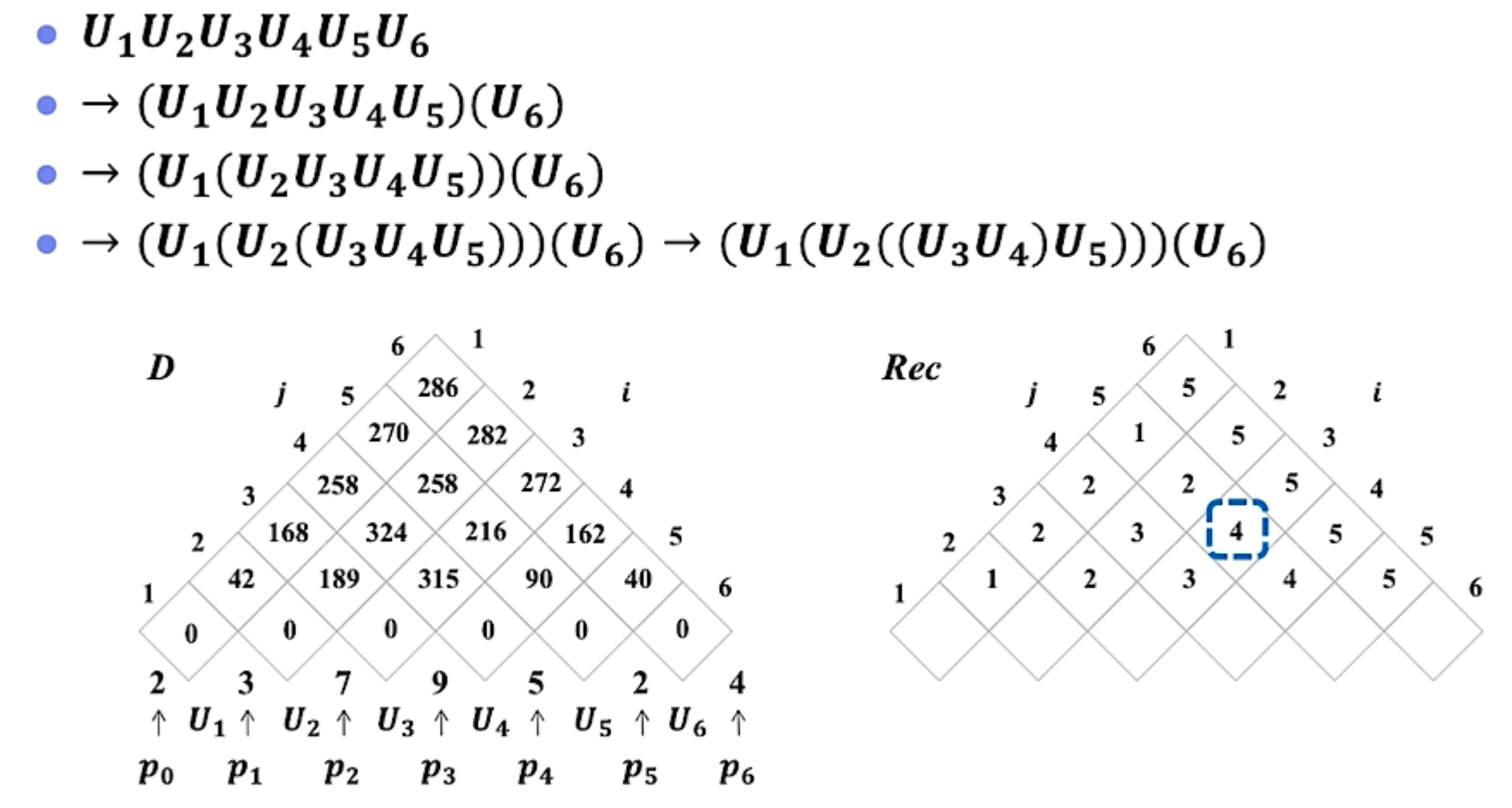
伪代码
输入:矩阵维度数组p,矩阵的个数n
输出:最小标量乘法次数,分割方式追踪数组Rec
新建二维数组D[1..n,1..n],Rec[1..n,1..n]
//初始化
for i <- 1 to n do
| D[i,i] <- 0
end
//动态规划
for l <- 2 to n do
| for i <- 1 to n-l+1 do
| | j <- i+l-1
| | for k <- i to j-1 do
| | | q <- D[i,k]+D[k+1,j]+p[i-1]*p[k]*p[j]
| | | if q<D[i,j] then
| | | | D[i,j] <- q
| | | | Rec[i,j] <- k
| | | end
| | end
| end
end
return D[1,n],Rec
时间复杂度 O ( n 3 ) O(n^3) O(n3)
相关文章:

(粗糙的笔记)动态规划
动态规划算法框架: 问题结构分析递推关系建立自底向上计算最优方案追踪 背包问题 输入: n n n个商品组成的集合 O O O,每个商品有两个属性 v i v_i vi和 p i p_i pi,分别表示体积和价格背包容量 C C C 输出: …...
Kaggle - LLM Science Exam上:赛事概述、数据收集、BERT Baseline
文章目录 一、赛事概述1.1 OpenBookQA Dataset1.2 比赛背景1.3 评估方法和代码要求1.4 比赛数据集1.5 优秀notebook 二、BERT Baseline2.1 数据预处理2.2 定义data_collator2.3 加载模型,配置trainer并训练2.4 预测结果并提交2.5 相关优化 前言:国庆期间…...

数据分析三剑客之一:Numpy详解及实战
1 NumPy介绍 NumPy 软件包是Python生态系统中数据分析、机器学习和科学计算的主力军。它极大地简化了向量和矩阵的操作处理。Python的一些主要软件包(如 scikit-learn、SciPy、pandas 和 tensorflow)都以 NumPy 作为其架构的基础部分。除了能对数值数据…...
【C语言】函数的定义、传参与调用(二)
💗个人主页💗 ⭐个人专栏——C语言初步学习⭐ 💫点击关注🤩一起学习C语言💯💫 目录 导读: 1. 函数的嵌套调用 1.1 什么是嵌套调用 1.2 基础实现 1.3 调用流程解析 2. 函数的链式访问 2.1 …...
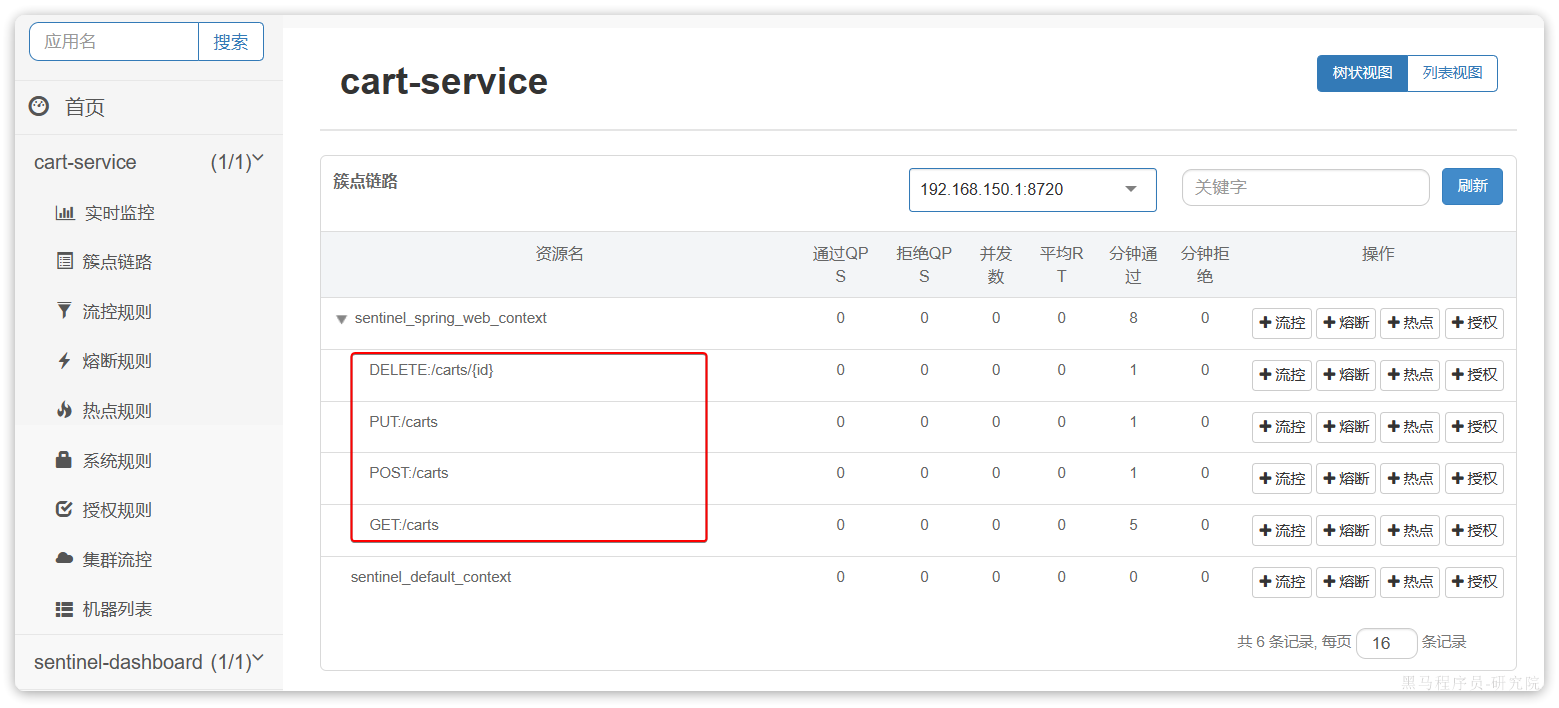
Sentinel安装
Sentinel 微服务保护的技术有很多,但在目前国内使用较多的还是Sentinel,所以接下来我们学习Sentinel的使用。 1.介绍和安装 Sentinel是阿里巴巴开源的一款服务保护框架,目前已经加入SpringCloudAlibaba中。官方网站: 首页 | Se…...
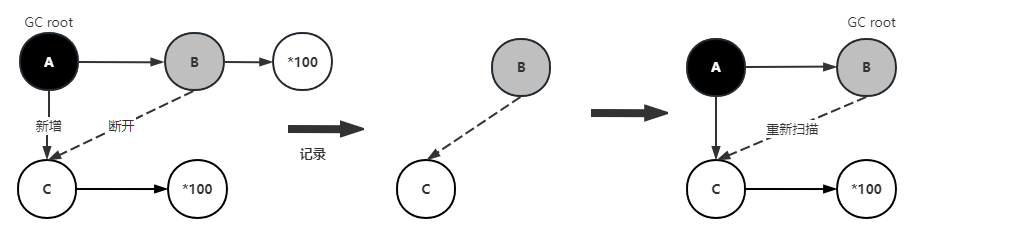
【JVM】并发可达性分析-三色标记算法
欢迎访问👋zjyun.cc 可达性分析 为了验证堆中的对象是否为可回收对象(Garbage)标记上的对象,即是存活的对象,不会被垃圾回收器回收,没有标记的对象会被垃圾回收器回收,在标记的过程中需要stop…...
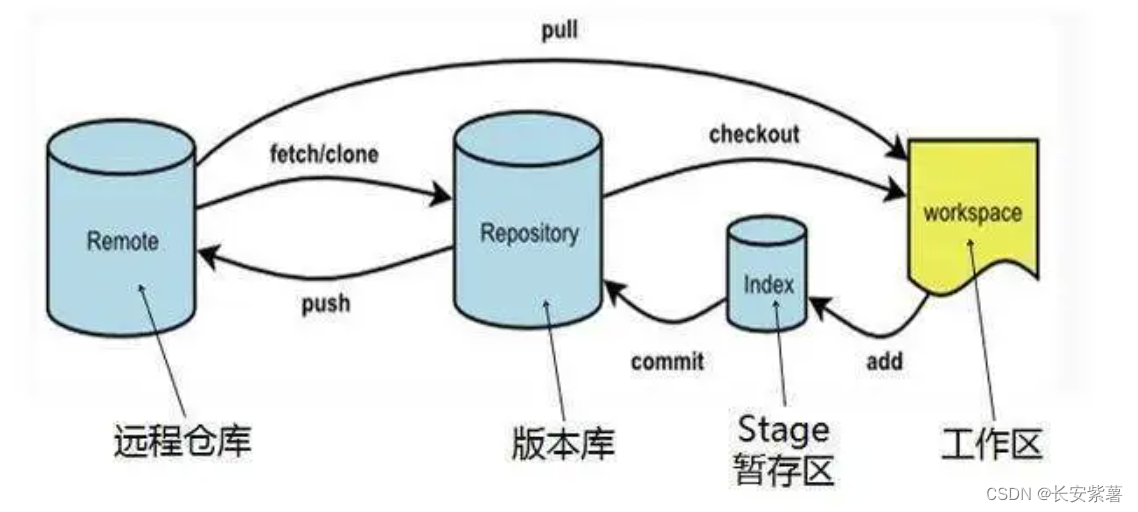
黑豹程序员-架构师学习路线图-百科:Git/Gitee(版本控制)
文章目录 1、什么是版本控制2、特点3、发展历史4、SVN和Git比较5、Git6、GitHub7、Gitee(国产)8、Git的基础命令 1、什么是版本控制 版本控制系统( Version Control )版本控制是一种管理和跟踪软件开发过程中的代码变化的系统。它…...
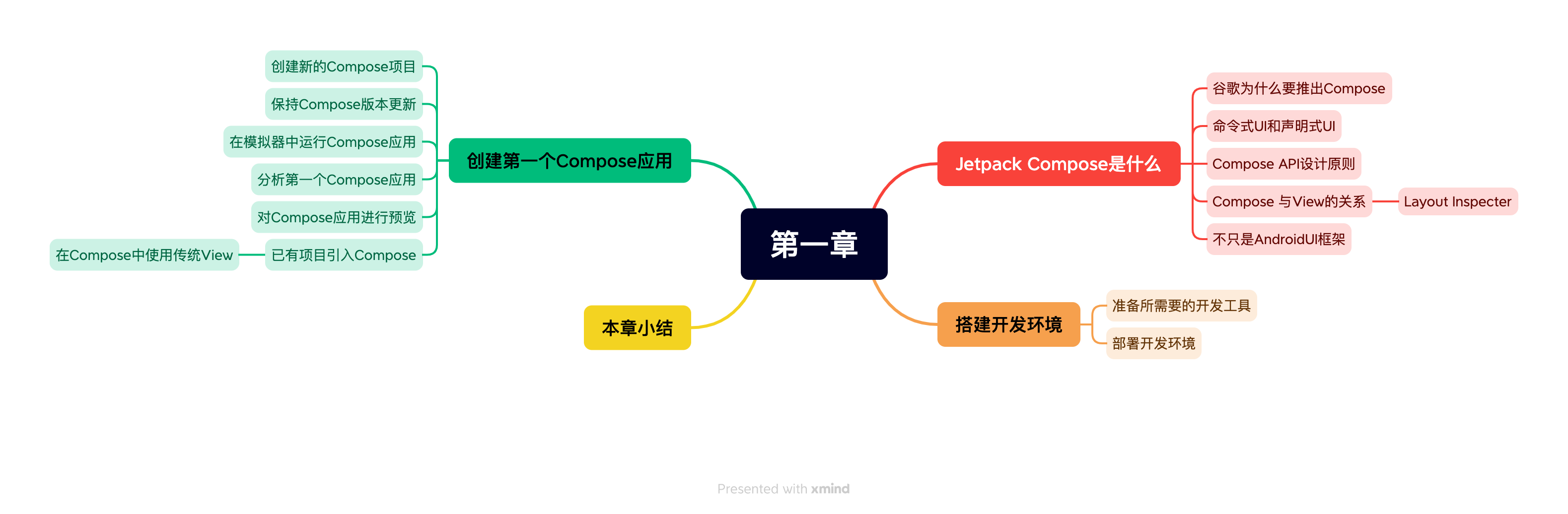
《Jetpack Compose从入门到实战》第一章 全新的 Android UI 框架
书籍源码 Compose官方文档 《Jetpack Compose从入门到实战》第一章 全新的 Android UI 框架 《Jetpack Compose从入门到实战》 第二章 了解常用UI组件 《Jetpack Compose从入门到实战》第三章 定制 UI 视图 《Jetpack Compose从入门到实战》第八章 Compose页面 导航 《Jet…...
基于Spring Boot的中小型医院网站的设计与实现
目录 前言 一、技术栈 二、系统功能介绍 前台首页界面 用户登录界面 用户注册界面 门诊信息详情界面 预约挂号界面 药品详情界面 体检报告界面 管理员登录界面 用户管理界面 医师管理界面 科室类型管理界面 门诊信息管理界面 药库信息管理界面 预约挂号管理界面…...

uniapp iOS离线打包——如何创建App并提交版本审核?
uniapp 如何创建App,并提交版本审核? 文章目录 uniapp 如何创建App,并提交版本审核?登录 appstoreconnect创建AppiOS 预览和截屏应用功能描述技术支持App 审核信息 App 信息内容版权年龄分级 价格与销售范围App 隐私提交审核 登录…...
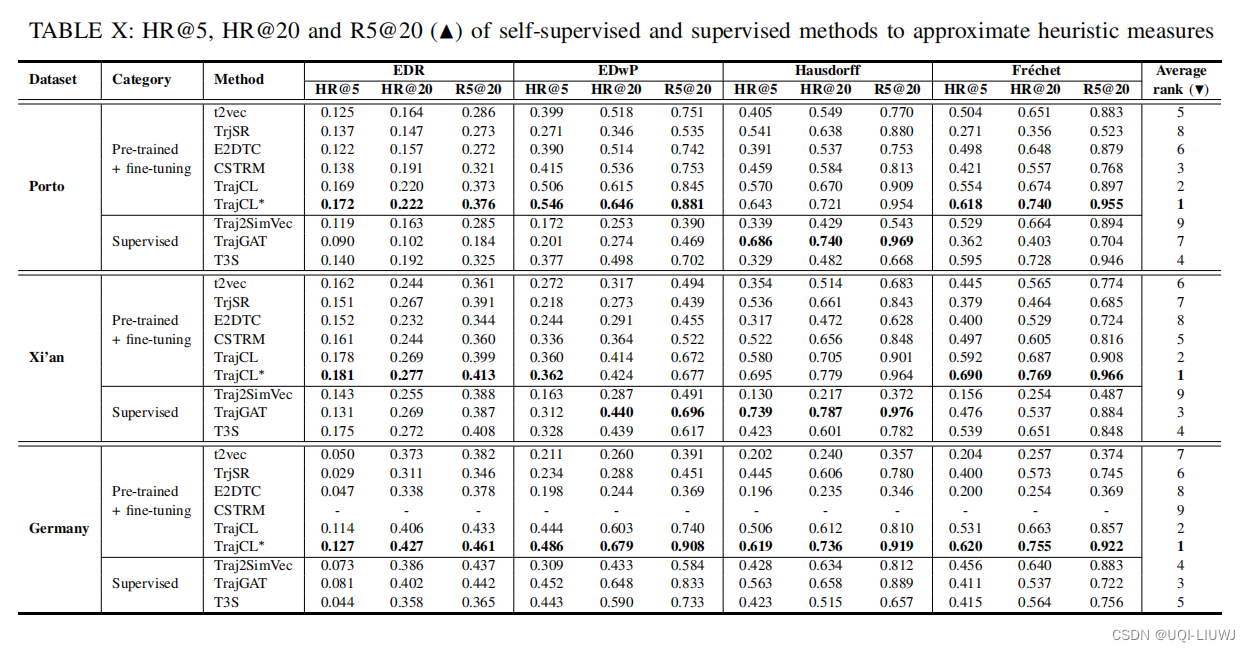
论文笔记:Contrastive Trajectory Similarity Learning withDual-Feature Attention
ICDE 2023 1 intro 1.1 背景 轨迹相似性,可以分为两类 启发式度量 根据手工制定的规则,找到两条轨迹之间基于点的匹配学习式度量 通过计算轨迹嵌入之间的距离来预测相似性值上述两种度量的挑战: 无效性: 具有不同采样率或含有噪…...

整数和字符串比较的坑
结果竟然是相同,惊呆了吧? $num1 2023快放假了; $num2 2023;if ($num1 $num2) {echo 相同; } else {echo 不相同; }num2改成字符串类型,结果:不相同,又不懵了吧? $num1 2023快放假了; $num2 2023;if…...

LeetCode 面试题 08.04. 幂集
文章目录 一、题目二、C# 题解 一、题目 幂集。编写一种方法,返回某集合的所有子集。集合中不包含重复的元素。 说明: 解集不能包含重复的子集。 示例: 输入: nums [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1…...

【m_listCtrl !=NULL有多个运算符与操作数匹配】2023/9/21 上午11:03:44
2023/9/21 上午11:03:44 m_listCtrl !=NULL有多个运算符与操作数匹配 2023/9/21 上午11:04:00 如果您在编译或运行代码时遇到"M_listCtrl != NULL有多个运算符与操作数匹配"的错误提示,这通常是由于以下几个原因之一: 错误使用运算符:在条件判断语句中,应该使…...

Logrus 集成 color 库实现自定义日志颜色输出字符原理
问题背景 下列代码实现了使用 Logurs 日志框架输出日志时根据级别不同,使用对应的自定义颜色进行输出。那么思考下代码的逻辑是怎么实现的呢? 效果如下: 代码如下: import ("fmt""github.com/sirupsen/logrus&q…...

【Java-LangChain:使用 ChatGPT API 搭建系统-2】语言模型,提问范式与 Token
第二章 语言模型,提问范式与 Token 在本章中,我们将和您分享大型语言模型(LLM)的工作原理、训练方式以及分词器(tokenizer)等细节对 LLM 输出的影响。我们还将介绍 LLM 的提问范式(chat format…...

想要精通算法和SQL的成长之路 - 最长连续序列
想要精通算法和SQL的成长之路 - 最长连续序列 前言一. 最长连续序列1.1 并查集数据结构创建1.2 find 查找1.3 union 合并操作1.4 最终代码 前言 想要精通算法和SQL的成长之路 - 系列导航 并查集的运用 一. 最长连续序列 原题链接 这个题目,如何使用并查集是一个小难…...
- 制图(Draft)-工程图框选制图曲线并输出制图曲线的信息)
UG NX二次开发(C#)- 制图(Draft)-工程图框选制图曲线并输出制图曲线的信息
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1、前言2、在UG NX中打开一个装配体模型3、进入工程制图模块,创建工程制图4、在VS中创建一个工程项目5、在Main()中添加选择的代码(UFun)6、在Main()中添加选择的代码(NXOpen)7、框选解决方案…...

1.7.C++项目:仿muduo库实现并发服务器之Poller模块的设计
项目完整在: 文章目录 一、Poller模块:描述符IO事件监控模块二、提供的功能三、实现思想(一)功能(二)意义(三)功能设计 四、封装思想五、代码(一)框架&#…...

Flutter笔记:build方法、构建上下文BuildContext解析
Flutter笔记 build 方法解析 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/133556333 本文主要介绍Flu…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
