代码随想录 Day10 栈与队列 LeetCode T239 滑动窗口的最大值 T347 前K个高频元素
简要介绍一下单调队列和优先级队列的不同
- 元素顺序的处理:单调队列中,元素的顺序是单调的,也就是说,队列中的元素按照特定的单调性(递增或递减)排列。这种特性使得单调队列在处理一些问题时非常高效,例如寻找滑动窗口中的最大值或最小值。优先队列则根据元素的优先级进行排序,优先级高的元素先出队。优先队列并不保证元素的单调性。
- 入队和出队的操作:在单调队列中,元素可以从队尾入队,但出队操作只能在队首进行。这是因为单调队列需要保持其单调性,所以新加入的元素需要放在合适的位置以维持这种单调性。优先队列则允许元素从任意位置入队,出队操作则总是发生在优先级最高的元素上。
- 队列长度:单调队列的长度取决于输入数据的合法性,如果输入数据不满足单调性要求,那么队列长度就可能为0。而优先队列的长度则始终与输入数据的数量等同,因为所有输入数据都会被放入队列中,只是出队的顺序会根据优先级有所不同。
更详细的题解和思路:代码随想录 (programmercarl.com)
LeetCode T239 滑动窗口的最大值
题目链接:239. 滑动窗口最大值 - 力扣(LeetCode)


题目思路
这道题有点难度,我们如果使用暴力求解的话是跑不过的,暴力方式就是遍历全部的数组,再遍历每K个元素的滑动窗口,分别找出最大值放入返回数组,这里我们不使用这个方式.
我们使用单调队列而不是优先级队列
因为优先级队列只能将最大的元素选出来,而下一步操作
1.创建单调队列,定义add,peek,poll方法
poll方法:如果移除元素等于队列的出口元素,弹出该元素
add方法:如果队尾元素比传入元素小,删除该元素,保证前方元素都大于我要传入的元素,从而保证单调队列的单调性
peek方法:因为单调队列维护了队头的最大元素,peek用来返回队头元素
2.实现函数
首先创建单调队列,先将前k个元素传入单调队列,获取其最大值,对k到数组结束的元素进行以下处理,先poll前k个元素,加入新的元素,比较得到最大值,最后返回最大值数组即可.
代码实现
class MyQue{Deque<Integer> que = new LinkedList<>();void poll(int val){if(!que.isEmpty() && val == que.peek()){que.poll();}}void add(int val){while(!que.isEmpty() && val>que.getLast()){que.removeLast();}que.add(val);}int peek(){return que.peek();}
}class Solution {public int[] maxSlidingWindow(int[] nums, int k) {if(nums.length == 1){return nums;}MyQue que = new MyQue();int len = nums.length;int num = 0;int[] res = new int[len-k+1];for(int i = 0;i<k;i++){que.add(nums[i]);}res[num++] = que.peek();for(int i = k;i<len;i++){que.poll(nums[i-k]);que.add(nums[i]);res[num++] = que.peek(); }return res;}
}LeetCode T347 前K个高频元素
题目链接:347. 前 K 个高频元素 - 力扣(LeetCode)

题目思路
首先创建一个map,key用来放置元素,value用来存放出现频率,这题我们就用到了优先级队列了,因为我们想用低于快排的时间复杂度解决问题,我们就只能使用大顶堆或小顶堆的数据结构,维护一个k个元素的堆来解决问题,最后将前k个元素依次pop出来即可.(这里为了简化代码使用了lambda表达式)
代码实现
class Solution {//解法1:基于大顶堆实现public int[] topKFrequent(int[] nums, int k) {Map<Integer,Integer> map = new HashMap<>();//key为数组元素值,val为对应出现次数for(int num:nums){map.put(num,map.getOrDefault(num,0)+1);}//在优先队列中存储二元组(num,cnt),cnt表示元素值num在数组中的出现次数//出现次数按从队头到队尾的顺序是从大到小排,出现次数最多的在队头(相当于大顶堆)PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2)->pair2[1]-pair1[1]);for(Map.Entry<Integer,Integer> entry:map.entrySet()){//大顶堆需要对所有元素进行排序pq.add(new int[]{entry.getKey(),entry.getValue()});}int[] ans = new int[k];for(int i=0;i<k;i++){//依次从队头弹出k个,就是出现频率前k高的元素ans[i] = pq.poll()[0];}return ans;}
} //解法2:基于小顶堆实现public int[] topKFrequent2(int[] nums, int k) {Map<Integer,Integer> map = new HashMap<>();//key为数组元素值,val为对应出现次数for(int num:nums){map.put(num,map.getOrDefault(num,0)+1);}//在优先队列中存储二元组(num,cnt),cnt表示元素值num在数组中的出现次数//出现次数按从队头到队尾的顺序是从小到大排,出现次数最低的在队头(相当于小顶堆)PriorityQueue<int[]> pq = new PriorityQueue<>((pair1,pair2)->pair1[1]-pair2[1]);for(Map.Entry<Integer,Integer> entry:map.entrySet()){//小顶堆只需要维持k个元素有序if(pq.size()<k){//小顶堆元素个数小于k个时直接加pq.add(new int[]{entry.getKey(),entry.getValue()});}else{if(entry.getValue()>pq.peek()[1]){//当前元素出现次数大于小顶堆的根结点(这k个元素中出现次数最少的那个)pq.poll();//弹出队头(小顶堆的根结点),即把堆里出现次数最少的那个删除,留下的就是出现次数多的了pq.add(new int[]{entry.getKey(),entry.getValue()});}}}int[] ans = new int[k];for(int i=k-1;i>=0;i--){//依次弹出小顶堆,先弹出的是堆的根,出现次数少,后面弹出的出现次数多ans[i] = pq.poll()[0];}return ans;简化版代码(避免一些api)
class Solution {public int[] topKFrequent(int[] nums, int k) {// 优先级队列,为了避免复杂 api 操作,pq 存储数组// lambda 表达式设置优先级队列从大到小存储 o1 - o2 为从大到小,o2 - o1 反之PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2) -> o1[1] - o2[1]);int[] res = new int[k]; // 答案数组为 k 个元素Map<Integer, Integer> map = new HashMap<>(); // 记录元素出现次数for(int num : nums) map.put(num, map.getOrDefault(num, 0) + 1);for(var x : map.entrySet()) { // entrySet 获取 k-v Set 集合// 将 kv 转化成数组int[] tmp = new int[2];tmp[0] = x.getKey();tmp[1] = x.getValue();pq.offer(tmp);if(pq.size() > k) {pq.poll();}}for(int i = 0; i < k; i ++) {res[i] = pq.poll()[0]; // 获取优先队列里的元素}return res;}
}相关文章:

代码随想录 Day10 栈与队列 LeetCode T239 滑动窗口的最大值 T347 前K个高频元素
简要介绍一下单调队列和优先级队列的不同 元素顺序的处理:单调队列中,元素的顺序是单调的,也就是说,队列中的元素按照特定的单调性(递增或递减)排列。这种特性使得单调队列在处理一些问题时非常高效&#…...

vue/自定义指令
需求: 页面有个input元素,现在要鼠标光标聚焦在上面,让每个页面上的标签都可以聚焦光标,比如,从A页面跳转到B页面的时候,我们依然要聚焦。如果要一遍遍地操作dom就会很麻烦。 这个时候,为了方便…...

借用binlog2sql工具轻松解析MySQL的binlog文件,再现Oracle的闪回功能
借用binlog2sql工具轻松解析MySQL的binlog文件 简介依赖配置用户权限选项配置案例:误UPDATE表数据回滚binlog2sql VS mysqlbinlog 看腻文章了就来听听视频演示吧:https://www.bilibili.com/video/BV1Zj411k7VW/ 简介 binlog2sql是美团大众点评开源的一…...

一次解决Pytorch训练时损失和参数出现Nan或者inf的经历
目前在做实验,参考了一个新的网络架构之后发现训练时损失出现Nan,参数了出现了inf的情况,先说说我的排查经历。 首先肯定是打印损失,损失是最容易出现Nan的,有各种原因,网上也有很多解决办法,我…...

【python入门篇】列表简介及操作(2)
列表是什么? 列表是由一系列按特定顺序排列的元素组成。你可以创建包含字母表中的所有字母、数字 0~9 或所有家庭成员的列表;也可以将任何东西加入列表中,其中的元素之间可以没有任何关系。列表通常包含多个元素,因此给列表指定一…...
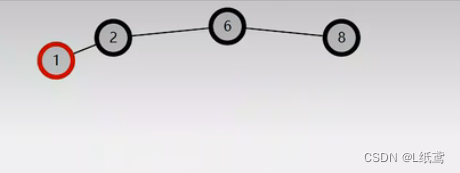
数据结构与算法——19.红黑树
这篇文章我们来讲一下红黑树。 目录 1.概述 1.1红黑树的性质 2.红黑树的实现 3.总结 1.概述 首先,我们来大致了解一下什么是红黑树 红黑树是一种自平衡的二叉查找树,是一种高效的查找树。红黑树具有良好的效率,它可在 O(logN) 时间内完…...
)
js题解(三)
文章目录 柯里化模块乘法改变上下文 柯里化 已知 fn 为一个预定义函数,实现函数 curryIt,调用之后满足如下条件: 1、返回一个函数 a,a 的 length 属性值为 1(即显式声明 a 接收一个参数) 2、调用 a 之后&a…...

CompletableFuture异步回调
CompletableFuture异步回调 CompletableFutureFuture模式CompletableFuture详解1.CompletableFuture的UML类关系2.CompletionStage接口3.使用runAsync和supplyAcync创建子任务4.设置子任务回调钩子5.调用handle()方法统一处理异常和结果6.线程池的使用 异步任务的串行执行thenA…...

Python中匹配模糊的字符串
嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 如何使用thefuzz 库,它允许我们在python中进行模糊字符串匹配。 此外,我们将学习如何使用process 模块,该模块允许我们在模糊…...
PHP图片文件管理功能系统源码
文件图库管理单PHP源码直接解压就能用,单文件,indexm.php文件可以重新命名,上传到需要访问的目录中, 可以查看目录以及各个文件,图片等和下载及修改管理服务。 源码下载:https://download.csdn.net/downloa…...

(枚举 + 树上倍增)Codeforces Round 900 (Div. 3) G
Problem - G - Codeforces 题意: 思路: 首先,目标值和结点权值是直接联系的,最值不可能直接贪心,一定是考虑去枚举一些东西,依靠这种枚举可以遍历所有的有效情况,思考的方向一定是枚举 如果去…...
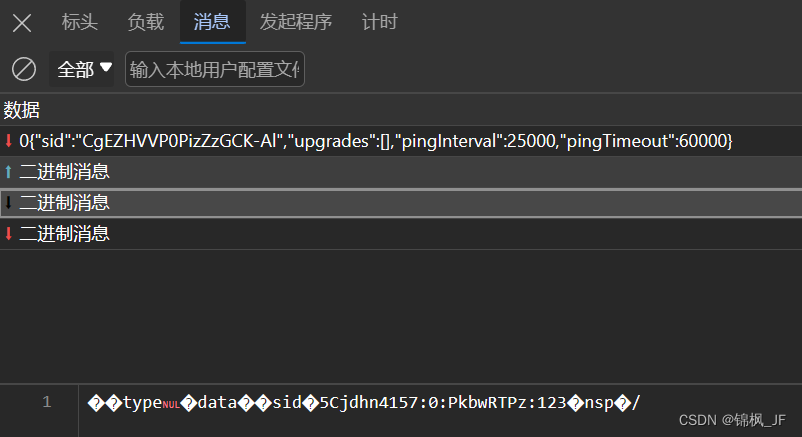
websocket逆向【python实现websocket拦截】
python实现websocket拦截 前言一、拦截的优缺点优点:缺点:二、实现方法1.环境配置2.代码三、总结前言 开发者工具F12,筛选ws后,websocket的消息是这样显示的,如何获取这里面的消息呢? 以下是本篇文章正文内容 一、拦截的优缺点 主要讲解一下websocket拦截的实现,现在…...

软件测试自动化的成本效益分析
随着软件测试技术的发展,人们已经从最初的手工测试转变为手工和自动化技术相结合的测试方法。目前,人们更多的是关心自动化测试框架、自动化测试工具以及脚本研究等技术方面,而在软件自动化测试方案的效益分析方面涉及较少。 软件测试的目的是…...

【Java】状态修饰符 final static
目录 final 修饰我们的成员方法、成员变量、类 示例代码: final 修饰的局部变量 示例代码: static 示例代码: static 访问特点: 示例代码: static关键字的用途 示例代码: static 修饰常量 示例…...

笔试编程ACM模式JS(V8)、JS(Node)框架、输入输出初始化处理、常用方法、技巧
目录 考试注意事项 先审完题意,再动手 在本地编辑器(有提示) 简单题515min 通过率0%,有额外log 常见输入处理 str-> num arr:line.split( ).map(val>Number(val)) 初始化数组 new Array(length).fill(v…...
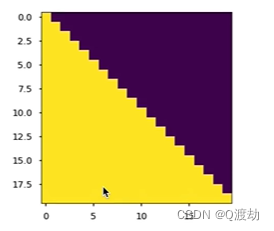
learn掩码张量
目录 1、什么是掩码张量 2、掩码张量的作用 3、代码演示 (1)、定义一个上三角矩阵,k0或者 k默认为 0 (2)、k1 (3)、k-1 4、掩码张量代码实现 (1)、输出效果 &…...
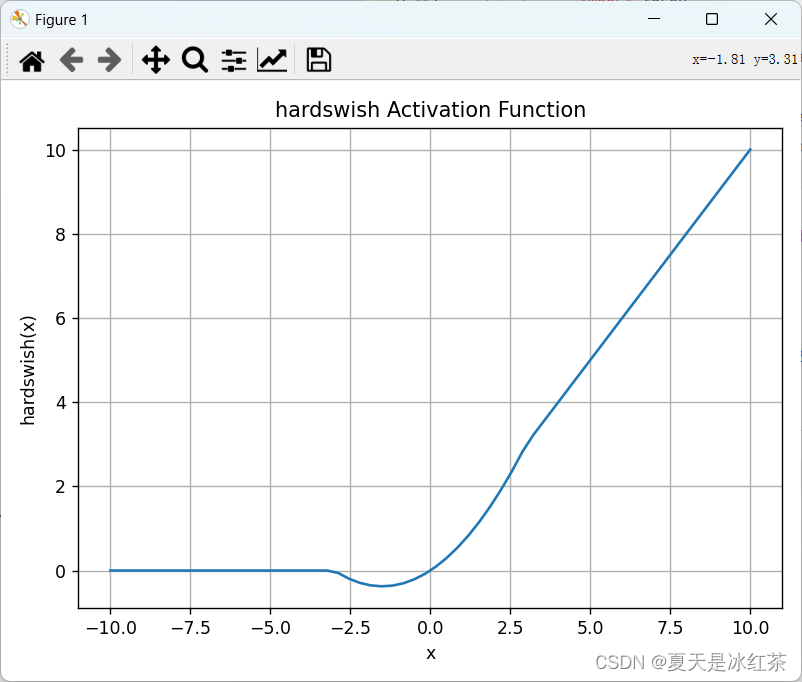
激活函数介绍
介绍 神经网络当中的激活函数用来提升网络的非线性,以增强网络的表征能力。它有这样几个特点:有界,必须为非常数,单调递增且连续可求导。我们常用的有sigmoid或者tanh,但我们都知道这两个都存在一定的缺点,…...
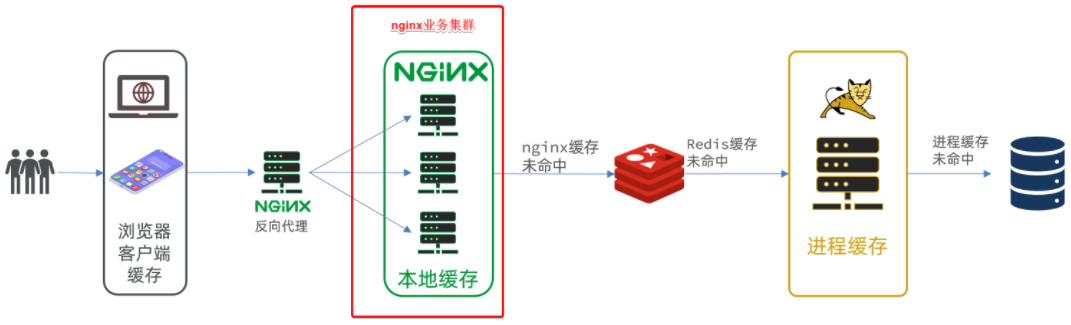
docker方式启动一个java项目-Nginx本地有代码,并配置反向代理
文章目录 案例导入说明1.安装MySQL1.1.准备目录1.2.运行命令1.3.修改配置1.4.重启 2.导入SQL3.导入Demo工程3.1.分页查询商品(仔细看代码,很多新的MP编程技巧)3.2.新增商品3.3.修改商品3.4.修改库存3.5.删除商品3.6.根据id查询商品3.7.根据id…...

前端和后端是Web开发选哪个好?
前端和后端是Web开发中的两个不同的领域,哪一种更适合学习?前景更广呢? 一、引言 Web前端开发就像装饰房间的小瓦匠,勤勤恳恳,仔仔细细,粉饰墙壁,妆点家具。会 HTML,CSS,懂点 JS。…...

HTTP协议,请求响应
、概述 二、HTTP请求协议 三、HTTP响应协议 四、请求数据 1.简单实体参数 RequestMapping("/simpleParam")public String simpleParam(RequestParam(name "name" ,required false ) String username, Integer age){System.out.println (username "…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
