数学建模Matlab之数据预处理方法
本文综合代码来自文章http://t.csdnimg.cn/P5zOD
异常值与缺失值处理
%% 数据修复
% 判断缺失值和异常值并修复,顺便光滑噪音,渡边笔记
clc,clear;close all;
x = 0:0.06:10;
y = sin(x)+0.2*rand(size(x));
y(22:34) = NaN; % 模拟缺失值
y(89:95) = 50;% 模拟异常值
testdata = [x' y'];subplot(2,2,1);
plot(testdata(:,1),testdata(:,2)); %subplot在一个图窗中创建多个子图,然后使用plot函数将原始数据可视化
title('原始数据');异常值检验
作者通常首先判断是否具有异常值,因为如果有异常值的话,咱们就会剔除异常值,使其变成缺失值,然后再做缺失值处理会好很多。
%% 判断数据中是否存在异常值
% 1.mean 三倍标准差法 2.median 离群值法 3.quartiles 非正态的离群值法
% 4.grubbs 正态的离群值法 5.gesd 多离群值相互掩盖的离群值法
choice_1 = 5;
yichangzhi_fa = char('mean', 'median', 'quartiles', 'grubbs','gesd');
yi_chang = isoutlier(y,strtrim(yichangzhi_fa(choice_1,:))); %选择的是gesd多离群值……
if sum(yi_chang)disp('数据存在异常值');
elsedisp('数据不存在异常值');
end对于上面的异常值检验法做讲解与扩展:
1. Mean 三倍标准差法(3σ原则)
- 描述:在正态分布数据中,任何一个数值如果偏离平均值超过3倍的标准差,就被认为是异常值。
- 应用条件:数据基本呈正态分布。(非常重要,需要进行正态性检验)
- 场景:适用于各种连续数据的分析,例如金融、生物统计等领域。
2. Median 离群值法
- 描述:基于中位数和四分位数范围来识别异常值。
- 应用条件:不需要数据完全符合正态分布。
- 场景:适用于偏态分布或者非正态分布的数据。
3. Quartiles 非正态的离群值法
- 描述:通过计算数据的四分位数范围(IQR)和上下四分位数来检测异常值。
- 应用条件:适用于非正态分布的数据。
- 场景:在各种非正态分布的数据分析中都可以使用。
4. Grubbs 正态的离群值法
- 描述:基于正态分布假设,测试数据集中最大或最小值是否显著偏离其余的观测值。
- 应用条件:数据应该是正态分布。
- 场景:广泛应用于各种领域,尤其是实验数据分析。
5. GESD(Generalized Extreme Studentized Deviate)
- 描述:用于检测多个异常值,即使它们相互掩盖。
- 应用条件:不特定于某一分布。
- 场景:当异常值可能相互掩盖时使用,例如在时间序列分析中。
其他方法
Tukey’s Fences:
- 通过四分位数范围(IQR)和“fences”(上下界)识别异常值。
- 适用于各种分布的数据。
DBSCAN(Density-Based Spatial Clustering of Applications with Noise):
- 一种基于密度的聚类算法,能够识别簇内和簇外点。
- 用于大数据集和空间数据。
Isolation Forests:
- 用于高维数据集的异常检测。
- 通过随机分离点来检测异常值。
正态性检验
读者不难发现,异常值检验通常与数据是否符合正态分布有关,所以,我们一起讨论一下如何使用matlab进行正态性检验。
初步判断
利用图像进行初步的正态性判断,涉及到常见的两种图:Q-Q图和P-P图。
PP图:
- PP图是用于比较两个数据集的累积分布函数(CDF)。
- 当你有一个样本数据集和一个理论分布(如正态分布)时,PP图会比较样本数据的CDF和理论CDF。
- 在正态PP图中,如果样本数据来自正态分布,那么数据点应该大致沿着45度线。
QQ图:
- QQ图是用于比较两个数据集的分位数。QQ图更常用于正态性检验,因为它对尾部的差异更敏感。
- 当你有一个样本数据集和一个理论分布时,QQ图会比较样本数据的分位数和理论分布的分位数。
- 在正态QQ图中,如果样本数据来自正态分布,那么数据点应该大致沿着一条直线,这条线不一定是45度线,但是应该是线性的。
其实上面最重要的一点就是,数据点在两个图中都沿着标准正态分布直线近似分布的话,我们就可以初步判断数据具有正态分布性。
% 正态检验
% 生成一些随机数据
data = randn(100, 1);% 创建一个新的图形窗口
figure;% 使用 normplot 创建正态概率图 (QQ图)
subplot(1,2,1);
normplot(data);
title('Normal Q-Q Plot');% 使用 probplot 创建PP图
subplot(1,2,2);
probplot('normal', data);
title('Normal P-P Plot');
可以在论文中这样写:
为了对数据集的分布特性进行深入理解和分析,本文采用了QQ图和PP图两种方法进行了初步的正态性检验,旨在从不同角度全面评估数据的分布状态。其结果如图1所示。

图1结果显示:在QQ图中,xx数据的尾部行为和中心趋势没有发现显著的异常值或者偏态现象,表现出良好的正态分布特征;在PP图中,xx数据的整体分布与正态分布非常接近,进一步证实了数据的正态性。综合以上分析结果可初步得知:xx数据集呈现出较强的正态分布特性。
尽管PP图和QQ图都是强大的工具,但它们主要用于探索性数据分析,并不能代替更正式的正态性检验方法,如Jarque-Bera测试或Lilliefors测试。
正式判断
% 正态检验
% 生成一些随机数据
data = randn(100, 1);% 使用 jbtest 进行 Jarque-Bera 测试
[h_jb, p_jb] = jbtest(data);% 使用 lillietest 进行 Lilliefors 测试
[h_lil, p_lil] = lillietest(data);% 显示测试结果
fprintf('Jarque-Bera Test: h = %d, p = %f\n', h_jb, p_jb);
fprintf('Lilliefors Test: h = %d, p = %f\n', h_lil, p_lil);
在上述代码中,h 和 p 分别代表假设检验的结果和 p 值,可以用来判断数据是否符合正态分布。
![]()
h = 0表示在给定的显著性水平下,不拒绝数据来自正态分布的原假设。即,数据可以被认为是正态分布的。p值是一个概率值,它表示观察到的数据与正态分布之间的差异是偶然产生的概率。一般来说,如果p值大于预定的显著性水平(例如,0.05),则接受原假设,认为数据是正态分布的。
故对上图结果进行数据分析(论文中写的多一点啊,这是简要版):
Jarque-Bera 测试结果:
h = 0, p = 0.361618- 因为
h为0,并且p值为0.361618(大于通常的显著性水平0.05),所以我们接受原假设,认为数据是正态分布的。Lilliefors 测试结果:
h = 0, p = 0.500000- 同样,
h为0,并且p值为0.5,这也指示数据是正态分布的。
异常值处理与缺失值判断
作者所有异常值处理都是先赋空值,不知道还有没有其他的方法……
%% 对异常值赋空值
F = find(yi_chang == 1);
y(F) = NaN; % 令数据点缺失
testdata = [x' y'];然后就可以和缺失值一起处理了,但是,为了保证文章的严谨性,咱还是需要判断一下是否存在缺失值。并且,不仅仅只判断,如果题目数据特征尤其多,并且有的特征缺失样本太多了,咱建议还是把这些特征删了,这就涉及到最省力法则:

% 假设testdata是一个n行m列的矩阵,每一列代表一个特征
[n, m] = size(testdata);
threshold = 0.8 * n; % 设置阈值,80%的总样本量% 遍历每一个特征
for i = 1:m% 计算每一列(特征)中非缺失值的数量nonMissingCount = sum(~isnan(testdata(:, i)));% 如果非缺失值的数量少于阈值,则删除该列(特征)if nonMissingCount < thresholdtestdata(:, i) = []; % 删除特征m = m - 1; % 更新特征数量i = i - 1; % 更新当前索引end
end% 显示处理后的数据
disp('处理后的数据:');
disp(testdata);
填充缺失值
%% 对数据进行补全
% 数据补全方法选择
% 1.线性插值 linear 2.分段三次样条插值 spline 3.保形分段三次样条插值 pchip
% 4.移动滑窗插补 movmean
chazhi_fa = char('linear', 'spline', 'pchip', 'movmean');
choice_2 = 3;
if choice_2 ~= 4testdata_1 = fillmissing(testdata,strtrim(chazhi_fa(choice_2,:))); % strtrim 是为了去除字符串组的空格
elsetestdata_1 = fillmissing(testdata,'movmean',10); % 窗口长度为 10 的移动均值
endsubplot(2,2,3);
plot(testdata_1(:,1),testdata_1(:,2));
title('数据补全结果');作者通常喜欢(让队友)使用K最近邻法填补,而且都是用python搞的,so这里不讲。
平滑处理
当然,可以根据实际情况进行数据的平滑处理:
%% 进行数据平滑处理
% 滤波器选择 1.Savitzky-golay 2.rlowess 3.rloess
choice_3 = 2;
lvboqi = char('Savitzky-golay', 'rlowess', 'pchip', 'rloess');
% 通过求 n 元素移动窗口的中位数,来对数据进行平滑处理
windows = 8;
testdata_2 = smoothdata(testdata_1(:,2),strtrim(lvboqi(choice_3,:)),windows) ;那么,实际情况到底是什么?
平滑数据对于某些机器学习模型的训练和性能是有益的,尤其是对于那些对数据中的噪声敏感的模型。下面是一些可能受益于数据平滑的算法:


决定是否进行数据平滑应该基于对上述因素的综合考虑,而不仅仅是基于特征的数量。在决定平滑之前,最好通过交叉验证来评估平滑对模型性能的实际影响。属于锦上添花的作用。
总结
最终的代码综合一下:
% 判断缺失值和异常值并修复,顺便光滑噪音,渡边笔记
clc,clear;close all;
x = 0:0.06:10;
y = sin(x)+0.2*rand(size(x));
y(22:34) = NaN; % 模拟缺失值
y(89:95) = 50;% 模拟异常值
testdata = [x' y'];subplot(2,2,1);
plot(testdata(:,1),testdata(:,2)); %subplot在一个图窗中创建多个子图,然后使用plot函数将原始数据可视化
title('原始数据');%% 判断数据中是否存在缺失值,并使用最省力法则
% 假设testdata是一个n行m列的矩阵,每一列代表一个特征
[n, m] = size(testdata);
threshold = 0.8 * n; % 设置阈值,80%的总样本量% 遍历每一个特征
for i = 1:m% 计算每一列(特征)中非缺失值的数量nonMissingCount = sum(~isnan(testdata(:, i)));% 如果非缺失值的数量少于阈值,则删除该列(特征)if nonMissingCount < thresholdtestdata(:, i) = []; % 删除特征m = m - 1; % 更新特征数量i = i - 1; % 更新当前索引end
end% 显示处理后的数据
disp('处理后的数据:');
disp(testdata);%% 判断数据中是否存在异常值
% 1.mean 三倍标准差法 2.median 离群值法 3.quartiles 非正态的离群值法
% 4.grubbs 正态的离群值法 5.gesd 多离群值相互掩盖的离群值法
choice_1 = 5;
yichangzhi_fa = char('mean', 'median', 'quartiles', 'grubbs','gesd');
yi_chang = isoutlier(y,strtrim(yichangzhi_fa(choice_1,:))); %选择的是gesd多离群值……
if sum(yi_chang)disp('数据存在异常值');
elsedisp('数据不存在异常值');
end%% 对异常值赋空值
F = find(yi_chang == 1);
y(F) = NaN; % 令数据点缺失
testdata = [x' y'];subplot(2,2,2);
plot(testdata(:,1),testdata(:,2));
title('去除差异值');%% 对数据进行补全
% 数据补全方法选择
% 1.线性插值 linear 2.分段三次样条插值 spline 3.保形分段三次样条插值 pchip
% 4.移动滑窗插补 movmean
chazhi_fa = char('linear', 'spline', 'pchip', 'movmean');
choice_2 = 3;
if choice_2 ~= 4testdata_1 = fillmissing(testdata,strtrim(chazhi_fa(choice_2,:))); % strtrim 是为了去除字符串组的空格
elsetestdata_1 = fillmissing(testdata,'movmean',10); % 窗口长度为 10 的移动均值
endsubplot(2,2,3);
plot(testdata_1(:,1),testdata_1(:,2));
title('数据补全结果');%% 进行数据平滑处理
% 滤波器选择 1.Savitzky-golay 2.rlowess 3.rloess
choice_3 = 2;
lvboqi = char('Savitzky-golay', 'rlowess', 'pchip', 'rloess');
% 通过求 n 元素移动窗口的中位数,来对数据进行平滑处理
windows = 8;
testdata_2 = smoothdata(testdata_1(:,2),strtrim(lvboqi(choice_3,:)),windows) ;subplot(2,2,4);
plot(x,testdata_2)
title('数据平滑结果');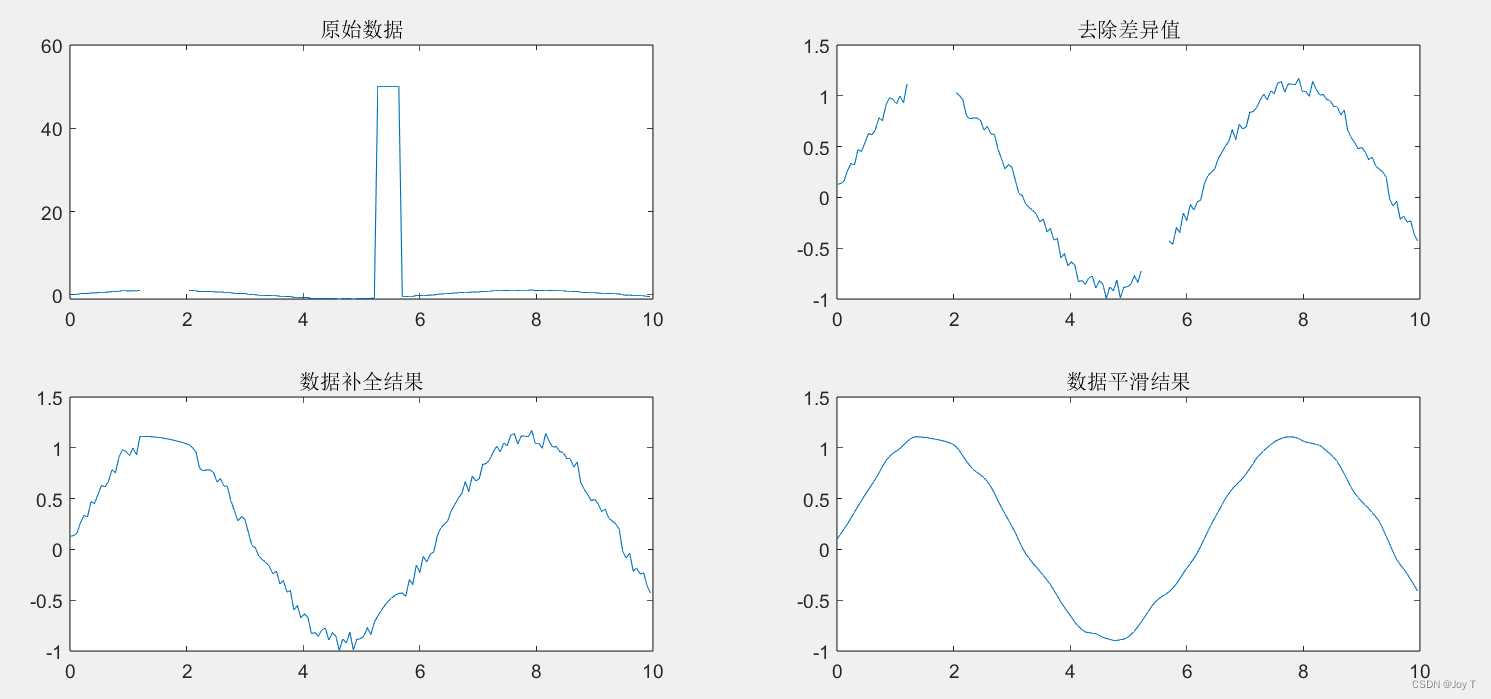
至此,数据预处理完成。
相关文章:

数学建模Matlab之数据预处理方法
本文综合代码来自文章http://t.csdnimg.cn/P5zOD 异常值与缺失值处理 %% 数据修复 % 判断缺失值和异常值并修复,顺便光滑噪音,渡边笔记 clc,clear;close all; x 0:0.06:10; y sin(x)0.2*rand(size(x)); y(22:34) NaN; % 模拟缺失值 y(89:95) 50;% 模…...

如何保证Redis的HA高可用
目录 1.关于Redis2.Redis 的使用场景3.Redis的高可用3.1 哨兵模式(Sentinel)3.2 集群模式(Cluster) 4.参考 本文主要介绍Redis如何保证高可用。 1.关于Redis Redis(Remote Dictionary Server)是一个开源的…...

第一百六十三回 如何在任意位置显示PopupMenu
文章目录 概念介绍使用方法示例代码 我们在上一章回中介绍了PopupMenuButton相关的内容,本章回中将介绍如何在任意位置显示PopupMenu.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在上一章回中介绍了PopupMenuButton相关的内容,它主…...

采用python中的opencv2的库来运用机器视觉移动物体
一. 此次我们来利用opencv2来进行机器视觉的学习 1. 首先我们先来进行一个小的案例的实现. 这次我们是将会进行一个小的矩形手势的移动. import cv2 from cvzone.HandTrackingModule import HandDetectorcap cv2.VideoCapture(0) # cap.set(3, 1280) # cap.set(4, 720) col…...

一、thymeleaf简介
1.1 什么是thymeleaf Thymeleaf是一个适用于web和独立环境的现代服务器端Java模板引擎,能够处理HTML、XML、JavaScript、CSS甚至纯文本。主要目标是提供一种优雅且高度可维护的创建模板的方法。 何为模板引擎呢?模板引擎就是为了使用户页面和业务数据…...

二分查找模版
对于一个递增序列我们要找大于等于target的数,返回结果的下标时 比如 序列 5 7 7 8 8 10 初始化左右指针l0 rn-1 猜测区间 [l,r] 闭区间,mid(lr)/2 防溢出就写成 midl(r-l)/2 如果有nums[mid]<target 那么[l,mid]这个区间的数就都小于target 更新 lmi…...

idea清空缓存类
解决办法 网上有很多是让你去清空什么maven依赖,但假如这个项目是你不可以大刀阔斧的话 可以清空idea缓存 选择 Invalidate 开头的 然后全选 运行重启idea OK...
 Practice(中文) 1015德才论)
PAT(Basic Level) Practice(中文) 1015德才论
前言 ※ PTA是 程序设计类实验辅助教学平台 ,里边包含一些编程题目集以供练习。 这道题用java解,我试了三种解法,不断优化,但始终是三个测试点通过、三个测试点超时。我把我的代码放在这里,做个参考吧。 1015 德才…...
接口自动化测试的概述及流程梳理~
接下来开始学习接口自动化测试。 因为之前从来没接触过,所以先了解一些基础知识。 1.接口测试的概述 2.接口自动化测试流程。 接口测试概述 接口,又叫API(Application Programming Interface,应用程序编程接口)&a…...
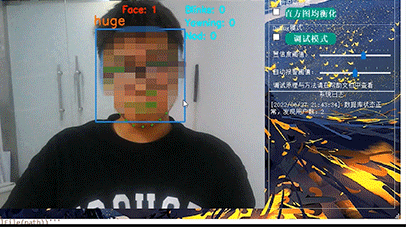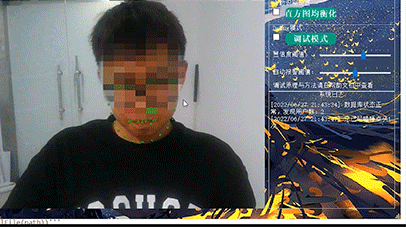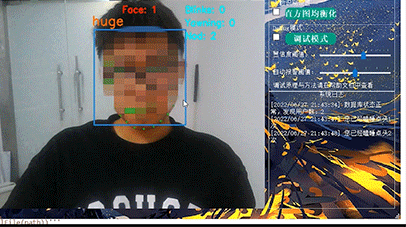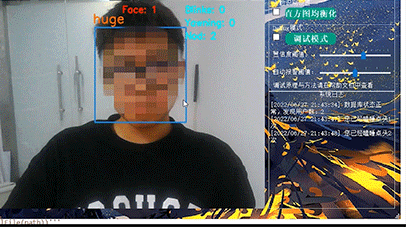
竞赛 机器视觉 opencv 深度学习 驾驶人脸疲劳检测系统 -python
文章目录 0 前言1 课题背景2 Dlib人脸识别2.1 简介2.2 Dlib优点2.3 相关代码2.4 人脸数据库2.5 人脸录入加识别效果 3 疲劳检测算法3.1 眼睛检测算法3.2 打哈欠检测算法3.3 点头检测算法 4 PyQt54.1 简介4.2相关界面代码 5 最后 0 前言 🔥 优质竞赛项目系列&#x…...
的运作)
虚拟货币(也称为加密货币或数字货币)的运作
虚拟币发展史 虚拟币的发展史可以追溯到20世纪末和21世纪初,以下是虚拟币的重要发展节点: 1998年:比特币白皮书的发布 比特币的概念最早由中本聪(Satoshi Nakamoto)在1998年提出,随后在2008年发布了一份名…...

N. Number Reduction
Problem - 1765N - Codeforces 发现如果是无前导0最小数那么在保证删除k个数时第1位是最小的,第二位一定是相对最小的,且答案第一位和第二位在原位置的间隔是小于等于还可以删除的位数的。 因此,对于原数字长度位n,要删除k&#…...

Java集合面试题
一、Java集合面试题 1.LinkedHashMap底层原理? HashMap是无序的,迭代HashMap所得到元素的顺序并不是它们最初放到HashMap的顺序,即不能保持它们的插入顺序。 LinkedHashMap继承于HashMap,是HashMap和LinkedList的融合体&#x…...

Python 编程基础 | 第三章-数据类型 | 3.5、列表
一、列表 1、创建列表 序列是Python中最基本的数据结构,Python有6个序列的内置类型,但最常见的是列表和元组。序列都可以进行的操作包括索引,切片,加,乘,检查成员。此外,Python已经内置确定序列…...
Spring Cloud Zuul 基本原理
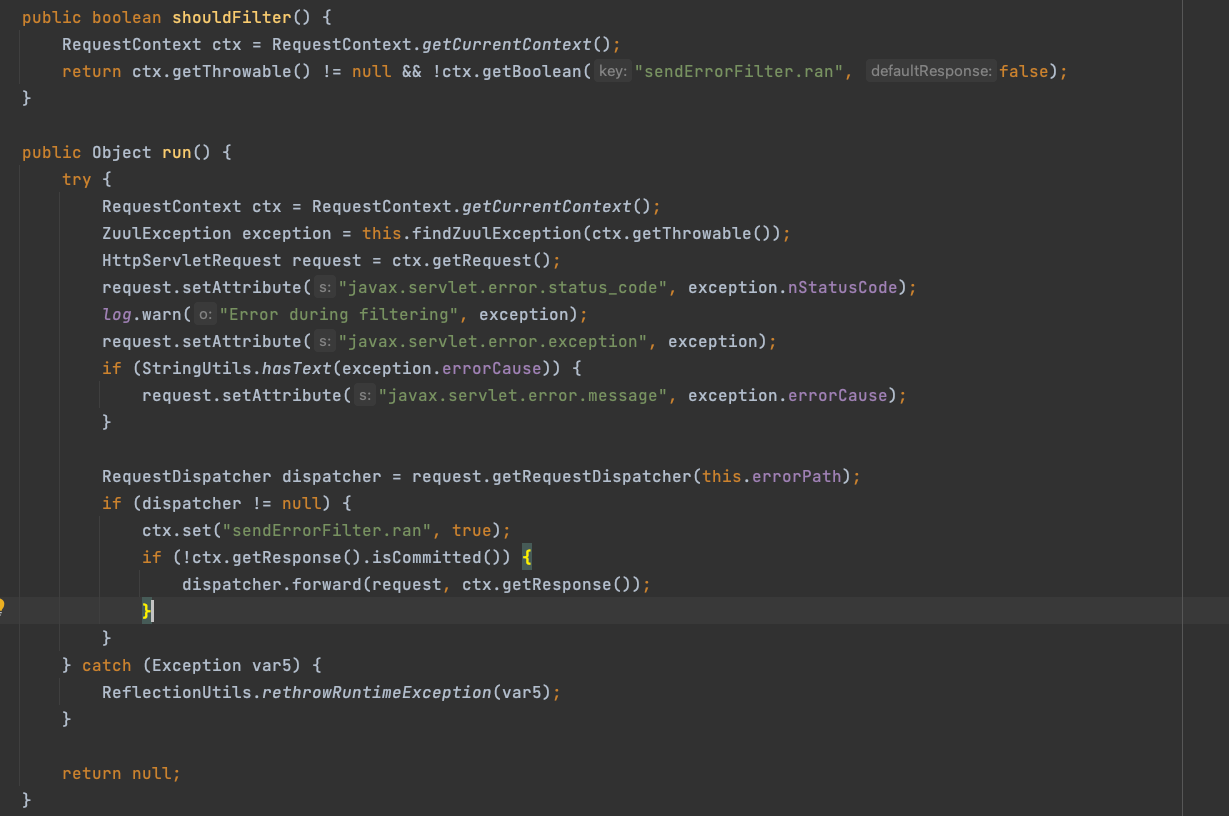
Spring Cloud Zuul 底层是基于Servlet实现的,核心是通过一系列的ZuulFilter来完成请求的转发。 1、核心组件注册 1.1. EnableZuulProxy注解 启用Zuul作为微服务网关,需要在Application应用类加上EnableZuulProxy注解,而该注解核心是利用Im…...
QT实现TCP服务器客户端的实现
ser: widget.cpp: #include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);//实例化一个服务器server new QTcpServer(this);// 此时…...
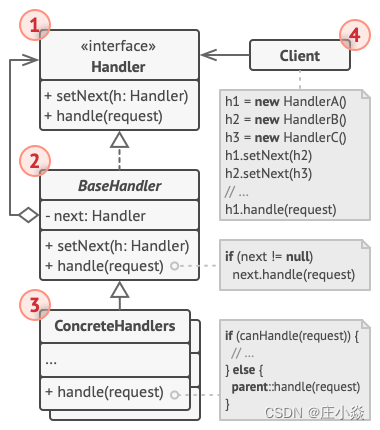
行为型设计模式——责任链模式
摘要 责任链模式(Chain of responsibility pattern): 通过责任链模式, 你可以为某个请求创建一个对象链. 每个对象依序检查此请求并对其进行处理或者将它传给链中的下一个对象。 一、责任链模式意图 职责链模式(Chain Of Responsibility) 是一种行为设…...
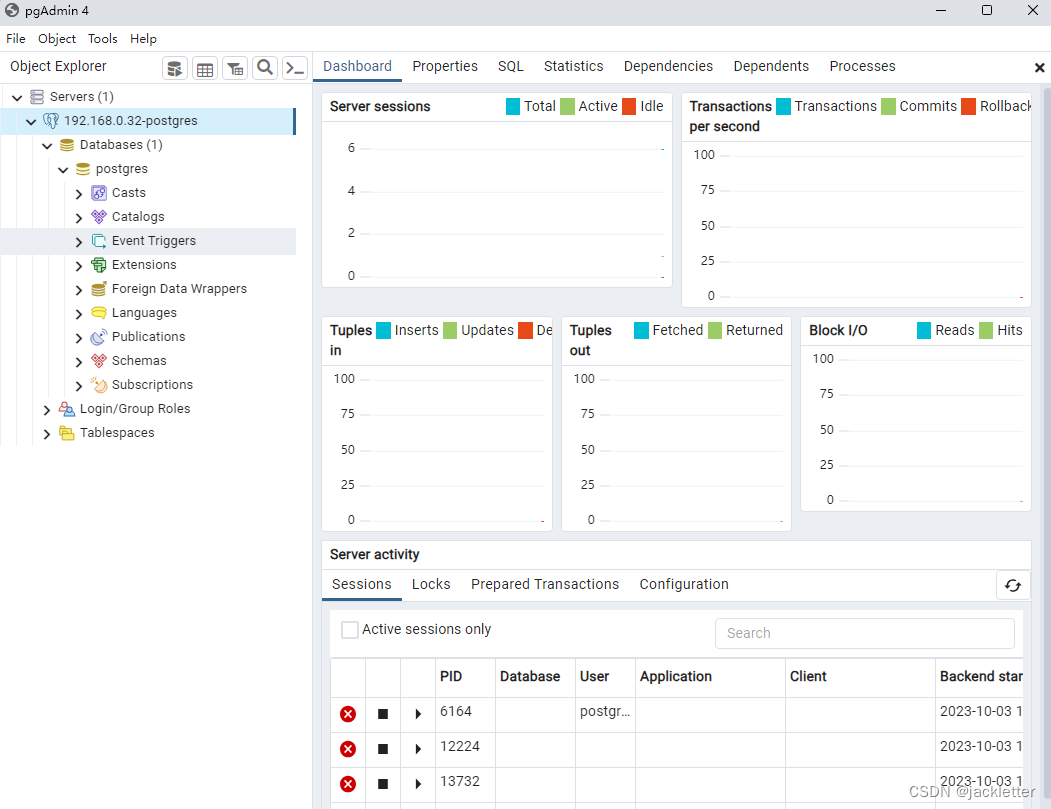
window安装压缩版postgresql
环境: window 11 专业版postgresql-16.0-1-windows-x64-binaries.zip 一、下载 1.1 从官网下载 https://www.postgresql.org/download/windows/ 1.2 从百度网盘下载 链接:https://pan.baidu.com/s/1fmQbgWSzX4hN07Lgdzfz0g?pwddzyy 提取码&#…...

数组(数据结构)
优质博文:IT-BLOG-CN 一、简介 数组Array是一种线性表数据结构,它用一组连续的内存空间,存储一组具有相同类型的数据。 数组因具有连续的内存空间的特点,数据拥有非常高效率的“随机访问”,时间复杂度为O(1)。但因要保…...

C/C++ 二分查找面试算法题
1.二分查找(有序数组) https://blog.csdn.net/qq_63918780/article/details/122527681 1 #include <stdio.h>2 #include <string.h>3 4 int func(int *a,int j,int x)5 {6 int len j - 1,i 0,min;7 while(i<len)8 {9 …...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
