C++算法 —— 动态规划(8)01背包问题
文章目录
- 1、动规思路简介
- 2、模版题:01背包
- 第一问
- 第二问
- 优化
- 3、分割等和子集
- 4、目标和
- 5、最后一块石头的重量Ⅱ
背包问题需要读者先明白动态规划是什么,理解动规的思路,并不能给刚接触动规的人学习。所以最好是看了之前的动规博客,才能看背包问题的所有博客,或者你本人就已经懂得动规了。
1、动规思路简介
动规的思路有五个步骤,且最好画图来理解细节,不要怕麻烦。当你开始画图,仔细阅读题时,学习中的沉浸感就体验到了。
状态表示
状态转移方程
初始化
填表顺序
返回值
动规一般会先创建一个数组,名字为dp,这个数组也叫dp表。通过一些操作,把dp表填满,其中一个值就是答案。dp数组的每一个元素都表明一种状态,我们的第一步就是先确定状态。
状态的确定可能通过题目要求来得知,可能通过经验 + 题目要求来得知,可能在分析过程中,发现的重复子问题来确定状态。还有别的方法来确定状态,但都大同小异,明白了动规,这些思路也会随之产生。状态的确定就是打算让dp[i]表示什么,这是最重要的一步。状态表示通常用某个位置为结尾或者起点来确定。
状态转移方程,就是dp[i]等于什么,状态转移方程就是什么。像斐波那契数列,dp[i] = dp[i - 1] + dp[i - 2]。这是最难的一步。一开始,可能状态表示不正确,但不要紧,大胆制定状态,如果没法推出转移方程,没法得到结果,那这个状态表示就是错误的。所以状态表示和状态转移方程是相辅相成的,可以帮你检查自己的思路。
要确定方程,就从最近的一步来划分问题。
初始化,就是要填表,保证其不越界。像第一段所说,动规就是要填表。比如斐波那契数列,如果要填dp[1],那么我们可能需要dp[0]和dp[-1],这就出现越界了,所以为了防止越界,一开始就固定好前两个值,那么第三个值就是前两个值之和,也不会出现越界。初始化的方式不止这一点,有些问题,假使一个位置是由前面2个位置得到的,我们初始化最一开始两个位置,然后写代码,会发现不够高效,这时候就需要设置一个虚拟节点,一维数组的话就是在数组0位置处左边再填一个位置,整个dp数组的元素个数也+1,让原先的dp[0]变为现在的dp[1],二维数组则是要填一列和一行,设置好这一行一列的所有值,原先数组的第一列第一行就可以通过新填的来初始化,这个初始化方法在下面的题解中慢慢领会。
第二种初始化方法的注意事项就是如何初始化虚拟节点的数值来保证填表的结果是正确的,以及新表和旧表的映射关系的维护,也就是下标的变化。
填表顺序。填当前状态的时候,所需要的状态应当已经计算过了。还是斐波那契数列,填dp[4]的时候,dp[3]和dp[2]应当都已经计算好了,那么dp[4]也就出来了,此时的顺序就是从左到右。还有别的顺序,要依据前面的分析来决定。
返回值,要看题目要求。
背包问题有很多种分类,此篇是关于01背包问题的。背包问题在写完代码都需要再做优化。所以比起之前的动规算法博客,背包问题的几篇博客都在最后加上一步优化。但优化方法只在模版题写,其它不写了。
2、模版题:01背包
DP41 【模板】01背包


第一问
先定dp[i]为从前i个物品选,选出最大价值的,这个其实是不行的,如果要选第i个物品,就需要看看背包满没满,但是现在的状态没法表示体积,所以不行。那就用二维数组,dp[i][j]表示从前i个物品中挑选,总体积不超过j,所有选法中,能选出的最大价值。
状态转移方程。根据最后一步来分析。我们可以选择第i个物品,也可以不选。如果不选,就是在0到i- 1中选,这个的结果放在dp[i -1][j]中;如果选择i位置的元素,也就是体积加上vi,那为了不超过背包,就得选择dp[i - 1][j - vi]位置的值加上wi,这个情况还有考虑,可能vi大于j了,所以j - vi需要>= 0。所以dp[i][j] = max(dp[i - 1][j - 1], dp[i - 1][j - vi] + wi)。
初始化,要加上一行一列,里面的值全都为0。返回值是最大值。
第二问
在第一问基础上来做改动。之前的dp[i][j]要从不超过j改成正好等于j。状态转移方程中,有可能选上一个后,仍然不够j。如果不选第i个物品,那么就是dp[i - 1][j],意思是在前i - 1个物品中选,体积等于j的最大价值,但有可能是达不到j的,我们先定义dp[i][j] = -1来表示没有这种情况,也就是前i个物品中没有能达到体积为j的选法。如果dp[i - 1][j]是-1,那么不选i位置的物品还是体积达不到j,所以不选的话就不用考虑了。选第i个物品的话,就要先看看dp[i - 1][j - vi]存不存在,不等于-1,也就是说前i - 1个位置正好达到了j - vi的体积,那么加上第i个物品就可行了。
初始化。新增行列,第一列整体都是0,第一行其余都是-1。
#include <iostream>
#include <cstring>
using namespace std;const int N = 1010;int n, V, v[N], w[N];
int dp[N][N];int main()
{cin >> n >> V;for(int i = 1; i <= n; i++){cin >> v[i] >> w[i];}for(int i = 1; i <= n; i++){for(int j = 1; j <= V; j++){dp[i][j] = dp[i - 1][j];if(j >= v[i]) dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}}cout << dp[n][V] << endl;//第一问memset(dp, 0, sizeof(dp));for(int j = 1; j <= V; j++) dp[0][j] = -1;for(int i = 1; i <= n; i++){for(int j = 1; j <= V; j++){dp[i][j] = dp[i - 1][j];if(j >= v[i] && dp[i - 1][j - v[i]] != -1) dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}}cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;return 0;
}
优化
数组很大,用滚动数组的思路来优化。仔细看一下分析,dp[i][j]由dp[i - 1][j]和dp[i - 1][j - vi]来决定,也就是这一行的一个元素由上一行的两个元素来决定,和其它行都没有关系,那么我们仅需要两行其实就是可以完成dp表的填写,根据第一行填完第二行后,第一行作为原先的第二行,第二行作为新的第二行继续更新数据。这就是滚动数组。但还可以减少空间。只用一行来进行操作。dp[j]由dp[j]和dp[j - vi]来决定,然后更新dp[j],用一行的话填表顺序就不能是从左到右,因为dp[j - vi]会把dp[j - vi]给换掉,所以填表顺序应当是从右到左,才能保证每个值都正确更新。
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;const int N = 1010;int n, V, v[N], w[N];
int dp[N];int main()
{cin >> n >> V;for(int i = 1; i <= n; i++){cin >> v[i] >> w[i];}for(int i = 1; i <= n; i++){for(int j = V; j >= v[i]; j--)//原本是j >= 1,在下面判断,但其实可以直接放在for括号里,减少循环次数{dp[j] = max(dp[j], dp[j - v[i]] + w[i]);}}cout << dp[V] << endl;//第一问memset(dp, 0, sizeof(dp));for(int j = 1; j <= V; j++) dp[j] = -1;for(int i = 1; i <= n; i++){for(int j = V; j >= v[i]; j--){if(dp[j - v[i]] != -1)dp[j] = max(dp[j], dp[j - v[i]] + w[i]);}}cout << (dp[V] == -1 ? 0 : dp[V]) << endl;return 0;
}
3、分割等和子集
416. 分割等和子集

可以转化成挑选一个数来达到是整体数组和的一半这个条件。并且,其实就是从前i个数中选,所有的选法中,能否凑齐j这个数,类型为bool,j就是sum / 2。
状态转移方程。如果不选i,那就看dp[i - 1][j];如果选i,那就是拿前面值加上i位置的值,假设前面的值是numi,那么这个位置应当在j - numi位置,但是j - numi必须存在才行。
初始化新增一行一列,第一列都是true,第一行其余位置都是false。
返回值是dp[n][sum / 2]。
bool canPartition(vector<int>& nums) {int n = nums.size(), sum = 0;for(auto x : nums) sum += x;if(sum % 2) return false;int aim = sum / 2;vector<vector<bool>> dp(n + 1, vector<bool>(aim + 1));for(int i = 0; i <= n; i++) dp[i][0] = true;for(int i = 1; i <= n; i++){for(int j = 1; j <= aim; j++){dp[i][j] = dp[i - 1][j];if(j >= nums[i - 1])dp[i][j] = dp[i][j] || dp[i - 1][j - nums[i - 1]];}}return dp[n][aim];}
但是这种做法实在不妥,按照滚动数组优化一下。
bool canPartition(vector<int>& nums) {int n = nums.size(), sum = 0;for(auto x : nums) sum += x;if(sum % 2) return false;int aim = sum / 2;vector<bool> dp(aim + 1);dp[0] = true;for(int i = 1; i <= n; i++){for(int j = aim; j >= nums[i - 1]; j--){dp[j] = dp[j] || dp[j - nums[i - 1]];}}return dp[aim];}
4、目标和
494. 目标和

根据题目,这些数字会被分为正数和负数,假设正数是a,负数绝对值是b,也就是说a + b = sum,a - b = target,所以a = (t + s) / 2,此时b就不见了。那么只用看a,也就是说选一些数,和正好是a,有多少种选法,就是答案。dp[i][j]就表示从前i个数中选,总和正好等于i,一共有多少种选法。
状态转移方程。如果选i,那么就看dp[i - 1][j nums[i]],因为是方法个数,所以不需要+nums[i];不选择i的话,就看dp[i - 1][j]。
初始化时,新增行列都是0,除了dp[0][0]是1。
返回值是最后一个值。优化部分直接写到代码上。
int findTargetSumWays(vector<int>& nums, int target) {int sum = 0;for(auto x: nums) sum += x;int aim = (sum + target) / 2;if(aim < 0 || (sum + target) % 2) return 0;int n = nums.size();vector<int> dp(aim + 1);dp[0] = 1;for(int i = 1; i <= n; i++){for(int j = aim; j >= nums[i - 1]; j--){dp[j] += dp[j - nums[i - 1]];}}return dp[aim];}
5、最后一块石头的重量Ⅱ
1049. 最后一块石头的重量 II

分析题目。每次拿到两个数字,按照题目去操作,其实就相当于一个正数和一个负数相加,得到一个值,是0就都没了,那么元素多了的话,就和上一题相似,一堆正数和一堆负数之间的运算。假设正数是a,负数的绝对值和是b,那么a + b = sum,求最小的a - b的值。从sum角度看,一个数字可以分成两个数字相加,如果这两个数字越接近sum的一半,那么就差值就越小。所以最终这个问题就转换成在数组中选择一些数,让这些数的和尽可能地接近sum / 2。
让dp[i][j]表示从前i个数中选,总和不超过j,此时的最大和。这个j就是sum / 2。如果选i,那就是dp[i - 1][j - nums[i]] + nums[i],如果不选i,那就是dp[i - 1][j],然后选出最大值。
初始化,新增行列都是0就可。
返回值返回sum - 2* dp[n][sum / 2]。优化直接写出来。
int lastStoneWeightII(vector<int>& stones) {int sum = 0;for(auto x : stones) sum += x;int n = stones.size(), m = sum / 2;vector<int> dp(m + 1);for(int i = 1; i <= n; i++){for(int j = m; j >= stones[i - 1]; j--){dp[j] = max(dp[j], dp[j - stones[i - 1]] + stones[i - 1]);}}return sum - 2 * dp[m];}
结束。
相关文章:

C++算法 —— 动态规划(8)01背包问题
文章目录 1、动规思路简介2、模版题:01背包第一问第二问优化 3、分割等和子集4、目标和5、最后一块石头的重量Ⅱ 背包问题需要读者先明白动态规划是什么,理解动规的思路,并不能给刚接触动规的人学习。所以最好是看了之前的动规博客࿰…...
ASUS华硕天选4笔记本FA507NU7735H_4050原装出厂Win11系统
下载链接:https://pan.baidu.com/s/1puxQOxk4Rbno1DqxhkvzXQ?pwdhkzz 系统自带网卡、显卡、声卡等所有驱动、出厂主题壁纸、Office办公软件、MyASUS华硕电脑管家、奥创控制中心等预装程序...

金蝶OA server_file 目录遍历漏洞
漏洞描述 金蝶OA server_file 存在目录遍历漏洞,攻击者通过目录遍历可以获取服务器敏感信息 漏洞影响 金蝶OA 漏洞复现 访问漏洞url: 漏洞POC Windows服务器: appmonitor/protected/selector/server_file/files?folderC://&suffi…...

read_image错误
File is no BMP-File(Halcon 错误代码5560)类似的错误一般都是图片内部封装的格式与外部扩展名不一致导致(也就是扩展名并不是真实图片的格式扩展)。 通过软件“UltraEdit”(http://www.onlinedown.net/soft/7752.htm)使用16进制查看&#x…...

文本分词排序
文本分词 在这个代码的基础上 把英语单词作为一类汉语,作为一类然后列出选项 1. 大小排序 2. 小大排序 3. 不排序打印保存代码 import jieba# 输入文本,让我陪你聊天吧~ lines [] print("请输入多行文本,以\"2333.3\"结束&am…...

SQL与关系数据库基本操作
SQL与关系数据库基本操作 文章目录 第一节 SQL概述一、SQL的发展二、SQL的特点三、SQL的组成 第二节 MySQL预备知识一、MySQL使用基础二、MySQL中的SQL1、常量(1)字符串常量(2)数值常量(3)十六进制常量&…...
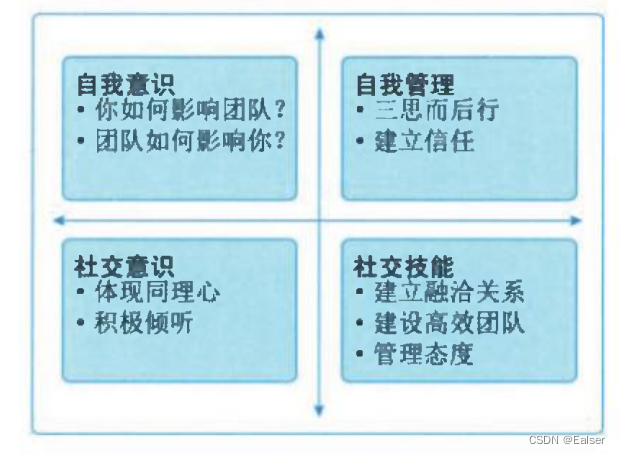
【2023年11月第四版教材】第18章《项目绩效域》(第一部分)
第18章《项目绩效域》(第一部分) 1 章节内容2 干系人绩效域2.1 绩效要点2.2 执行效果检查2.3 与其他绩效域的相互作用 3 团队绩效域3.1 绩效要点3.2 与其他绩效域的相互作用3.3 执行效果检查3.4 开发方法和生命周期绩效域 4 绩效要点4.1 与其他绩效域的相…...
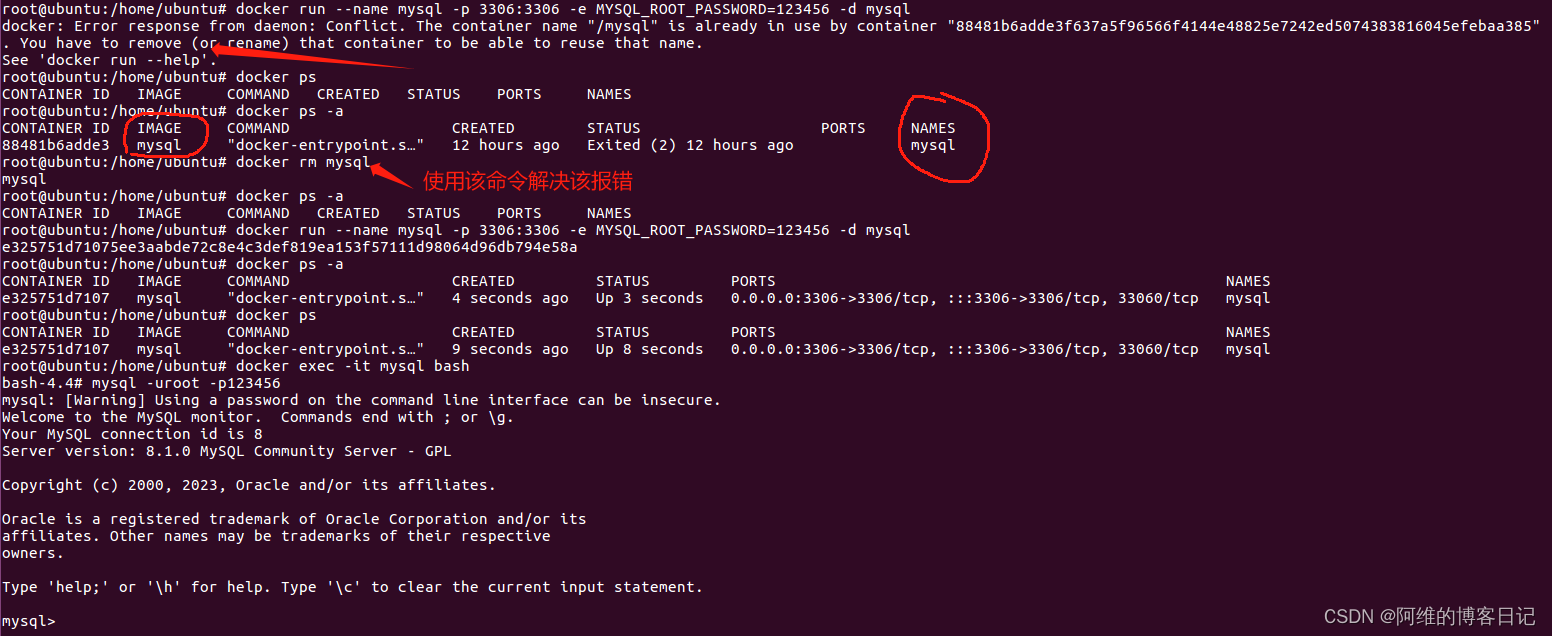
Docker启动Mysql
如果docker里面没有mysql需要先pull一个mysql镜像 docker pull mysql其中123456是mysql的密码 docker run --name mysql -p 3306:3306 -e MYSQL_ROOT_PASSWORD123456 -d mysql可以使用如下命令进入Mysql的命令行界面 docker exec -it mysql bash登录mysql使用如下命令,root是…...

QScrollArea样式
简介 QScrollBar垂直滚动条分为sub-line、add-line、add-page、sub-page、up-arrow、down-arrow和handle几个部分。 QScrollBar水平滚动条分为sub-line、add-line、add-page、sub-page、left-arrow、right-arrow和handle几个部分。 部件如下图所示: 样式详…...
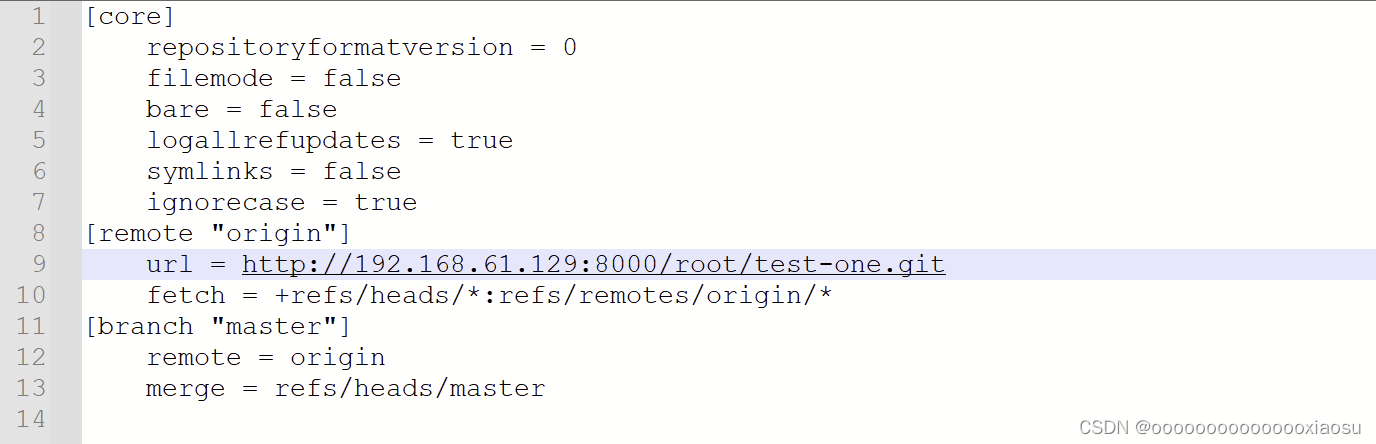
【gitlab】git push -u origin master 报403
问题描述 gitlab版本:14.0.5 虚拟机版本:centos7 项目:renren-fast 原因分析 .git -> config目录下 url配错 但这个url不是手动配置的,还不知道怎么生成。 解决方法 把配置错误的url改成gitlab的project的url 这样&#…...

第二篇:矩阵的翻转JavaScript
一维数组的翻转 // 一维矩阵翻转 // 实例: arr [1,2,3,4,5] > [5,4,3,2,1] let n readline() let arr readline().split( ).map(Number) // console.log(n,arr) let temp 0 for(let i 0; i < n/2;i){temp arr[i]arr[i] arr[n-i-1]arr[n-i-1] temp }…...
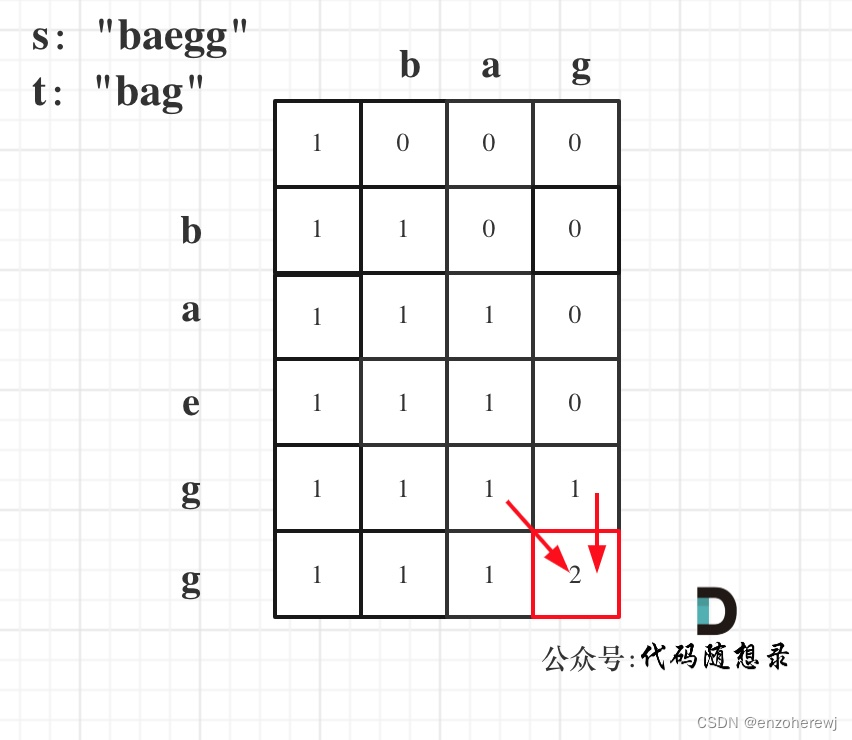
代码随想录算法训练营第五十七天 | 动态规划 part 15 | 392.判断子序列、115.不同的子序列
目录 392.判断子序列思路代码 115.不同的子序列思路代码 392.判断子序列 Leetcode 思路 dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]递推公式: 初始化:为0遍历顺序ÿ…...

【国漫逆袭】人气榜,小医仙首次上榜,霍雨浩排名飙升,不良人热度下降
Hello,小伙伴们,我是小郑继续为大家深度解析国漫资讯。 为了提升作品和角色的讨论度,增加平台的用户活跃度,小企鹅推出了动漫角色榜,该榜单以【年】【周】【日】为单位,通过角色的点赞量和互动量进行排名 上周的动漫角…...

国庆中秋特辑(七)Java软件工程师常见20道编程面试题
以下是中高级Java软件工程师常见编程面试题,共有20道。 如何判断一个数组是否为有序数组? 答案:可以通过一次遍历,比较相邻元素的大小。如果发现相邻元素的大小顺序不对,则数组不是有序数组。 public boolean isSort…...
长剖与贪心+树上反悔贪心:1004T4
长剖的本质是一种贪心。(启发式合并本质也是类似哈夫曼树的过程) 在此题中,首先肯定变直径,然后选端点为根。然后选叶子。而每个叶子为了不重复计算,可以只计算其长剖后所在链的贡献。(本题精髓࿰…...

二叉树经典例题
前言: 本文主要讲解了关于二叉树的简单经典的例题。 因为二叉树的特性,所以关于二叉树的大部分题目,需要利用分治的思想去递归解决问题。 分治思想: 把大问题化简成小问题(根节点、左子树、右子树)&…...

什么是指针的指针和指向函数的指针?
理解指针的指针和指向函数的指针对于C语言初学者来说可能会有些挑战,但它们都是非常重要的概念,可以帮助你更好地理解和利用C语言的强大功能。在本文中,我将详细解释这两个概念,包括它们的概念、用途和示例。 指针的指针…...
多个excel合并
目的:将同一个文件下的多个 “京东差评.xlsx” 合并为一个:“京东汇总.xlsx" 代码如下: # -*- coding: utf-8 -*- """ Created on Wed Oct 4 12:52:32 2023author: 64884 """import pandas as pd impor…...
Integrity Plus for Mac,保障网站链接无忧之选
在如今数字化的时代,网站链接的完整性对于用户体验和搜索引擎排名至关重要。如果您是一位网站管理员或者经常需要检查网站链接的人,那么Integrity Plus for Mac(Integrity Plus)将成为您最好的伙伴。 Integrity Plus是一款专业的…...

C#,数值计算——Sobol拟随机序列的计算方法与源程序
1 文本格式 using System; using System.Collections.Generic; namespace Legalsoft.Truffer { /// <summary> /// Sobol quasi-random sequence /// </summary> public class Sobol { public Sobol() { } public static void sobseq(int n,…...

DBA 经验:MySQL性能最重要的参数只有2个!
在日常的MySQL性能优化工作中,面对几百个配置参数,常常让人眼花缭乱。但经过多年的实战经验,我发现真正起决定性作用的参数其实只有两个。今天,我就把这压箱底的经验分享给大家——调好这两个参数,你的MySQL性能就成功…...

为什么选择matrixmultiplication.xyz?5大优势让线性代数学习事半功倍
为什么选择matrixmultiplication.xyz?5大优势让线性代数学习事半功倍 【免费下载链接】matrixmultiplication.xyz 项目地址: https://gitcode.com/gh_mirrors/ma/matrixmultiplication.xyz matrixmultiplication.xyz是一款专为教育设计的交互式矩阵乘法计算…...

Obsidian Admonition效率提升:10个你必须知道的实用技巧
Obsidian Admonition效率提升:10个你必须知道的实用技巧 【免费下载链接】admonitions 项目地址: https://gitcode.com/gh_mirrors/adm/admonitions Obsidian Admonition是一款强大的插件,能够帮助用户在Obsidian笔记中创建丰富多样的提示框&…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
