数据结构-优先级队列(堆)
文章目录
目录
文章目录
前言
一 . 堆
二 . 堆的创建(以大根堆为例)
堆的向下调整(重难点)
堆的创建
堆的删除
向上调整
堆的插入
三 . 优先级队列
总结
前言
大家好,今天给大家讲解一下堆这个数据结构和它的实现 - 优先级队列
一 . 堆
堆(Heap)是一种基于完全二叉树的数据结构,具有以下特点:
-
完全二叉树:堆是一种完全二叉树,即除了最后一层外,其他层的节点都是满的,并且最后一层的节点都靠左排列。
-
堆序性:堆中的每个节点都满足堆序性质,即对于最大堆(Max Heap),父节点的值大于或等于其子节点的值;对于最小堆(Min Heap),父节点的值小于或等于其子节点的值。
堆通常用数组来实现,其中数组的索引表示节点在堆中的位置。对于一个节点在索引i的堆,其左子节点在索引2i,右子节点在索引2i+1,父节点在索引i/2。
堆常常被用来实现优先级队列,因为它能够快速找到最大或最小的元素,并且在插入和删除操作时保持堆序性质。
常见的堆有两种类型:
-
最大堆(大根堆):父节点的值大于或等于其子节点的值。最大堆的根节点是堆中的最大元素。
-
最小堆(小根堆):父节点的值小于或等于其子节点的值。最小堆的根节点是堆中的最小元素。
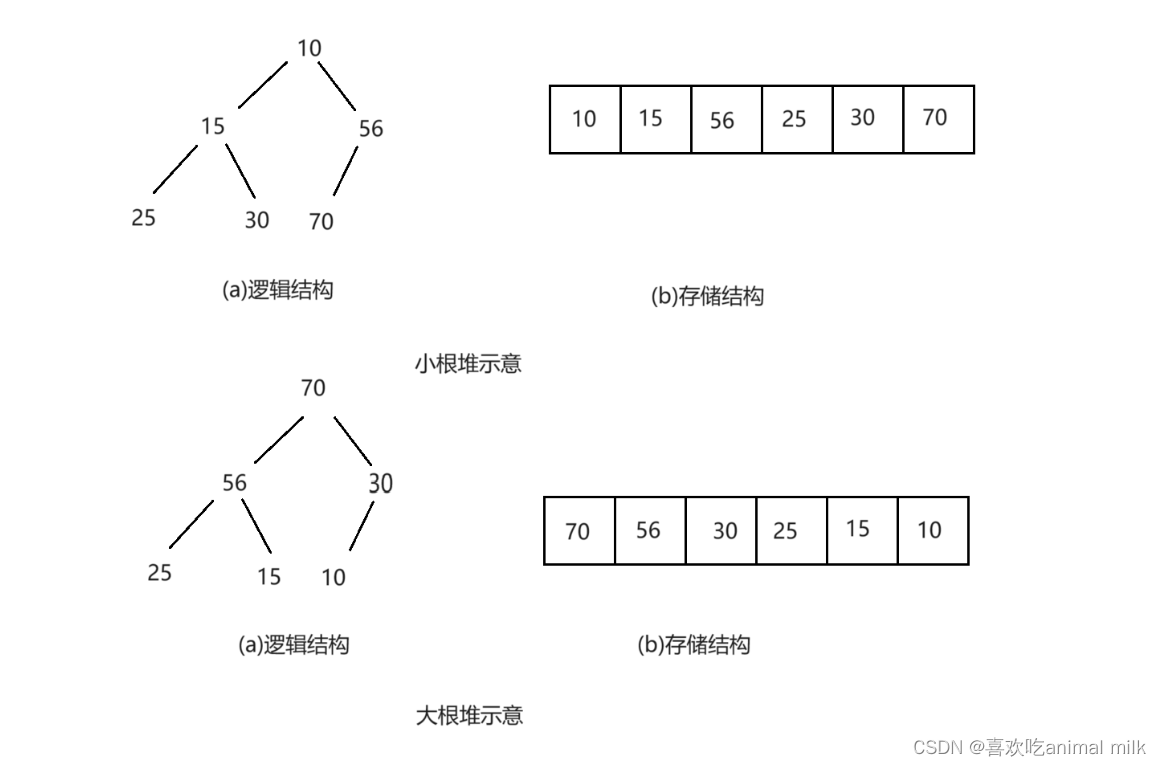
堆的常见操作包括:
-
插入(Insertion):将一个元素插入到堆中,需要保持堆序性质。
-
删除根节点(Delete Root):删除堆中的根节点,需要调整堆以保持堆序性质。
-
查找最大/最小元素(Find Max/Min):在最大堆中查找最大元素,在最小堆中查找最小元素,时间复杂度为O(1)。
-
堆排序(Heap Sort):利用堆的性质进行排序,时间复杂度为O(nlogn)。
二 . 堆的创建(以大根堆为例)
初始化工作
public class BigHeap {int[] elem; // 用来记录堆中的元素int size;public BigHeap(int capacity) {elem = new int[capacity];}//再初始化的时候默认给一个数组public void initHeap(int[] arr) {for (int i = 0; i < arr.length; i++) {elem[i] = arr[i];size++;}}public boolean isFull() {return elem.length == size;}public void swap(int i,int j){int temp = elem[i];elem[i] = elem[j];elem[j] = temp;}}
堆的向下调整(重难点)
对于集合{ 27,15,19,18,28,34,65,49,25,37 }中的数据,如果将其创建成大根堆呢?
父节点的值大于或等于其子节点的值。最大堆的根节点是堆中的最大元素。
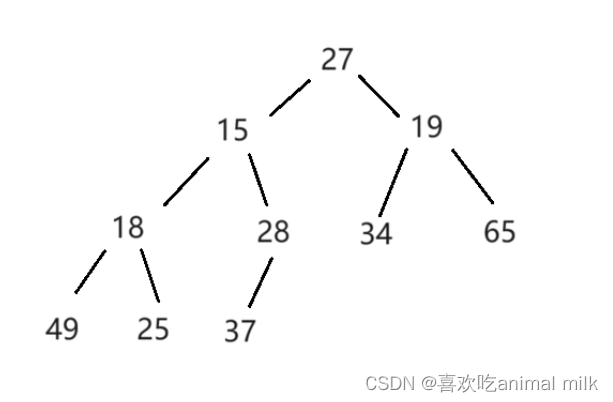
根据层序遍历构建出的二叉树显然并不符合我们的要求,这个是时候我们就需要进行向下调整
在最大堆中,向下调整的过程是将当前节点与其子节点中较大的节点进行比较,如果当前节点小于其中较大的子节点,就将它们交换位置。然后,继续向下比较和交换,直到当前节点不再小于其子节点或者已经到达叶子节点。
思考一下,这个时候我们应该从哪个节点进行调整?
我们通常是从最后一个非叶子节点开始向下调整,直到根节点或者到达叶子节点为止。从最后一个非叶子节点开始向下调整的原因是,只有非叶子节点才有子节点,而叶子节点没有子节点,所以没有必要对叶子节点进行向下调整操作。
最后一个非叶子节点的索引可以通过公式计算得到:n/2-1,其中n是堆中元素的数量。
步骤
1. 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子,因为是完全二叉树)
2. 如果parent的左孩子存在,即:child < len, 进行以下操作,直到parent的左孩子不存在
- parent右孩子是否存在,存在找到左右孩子中最大的孩子,让child进行标记
- 将parent与较大的孩子child比较如果:
- parent小大于较大的孩子child,调整结束
- 否则:交换parent与较大的孩子child,交换完成之后,parent中小的元素向下移动,可能导致子树不满足堆的性质,因此需要继续向下调整,即parent = child;child = parent*2+1; 然后继续2(上面的)。
图解
{ 27,15,19,18,28,34,65,49,25,37 }
len: 数组的长度
parent: 表示指向需要调整的节点指针
child: 表示指向孩子节点的指针
最后一个非叶子节点: 根据公式parent = (child-1)/2 在这里child表示最后一个节点的索引
parent = (len - 1 - 1)/2 = 4 我们应该从4索引开始进行向下调整
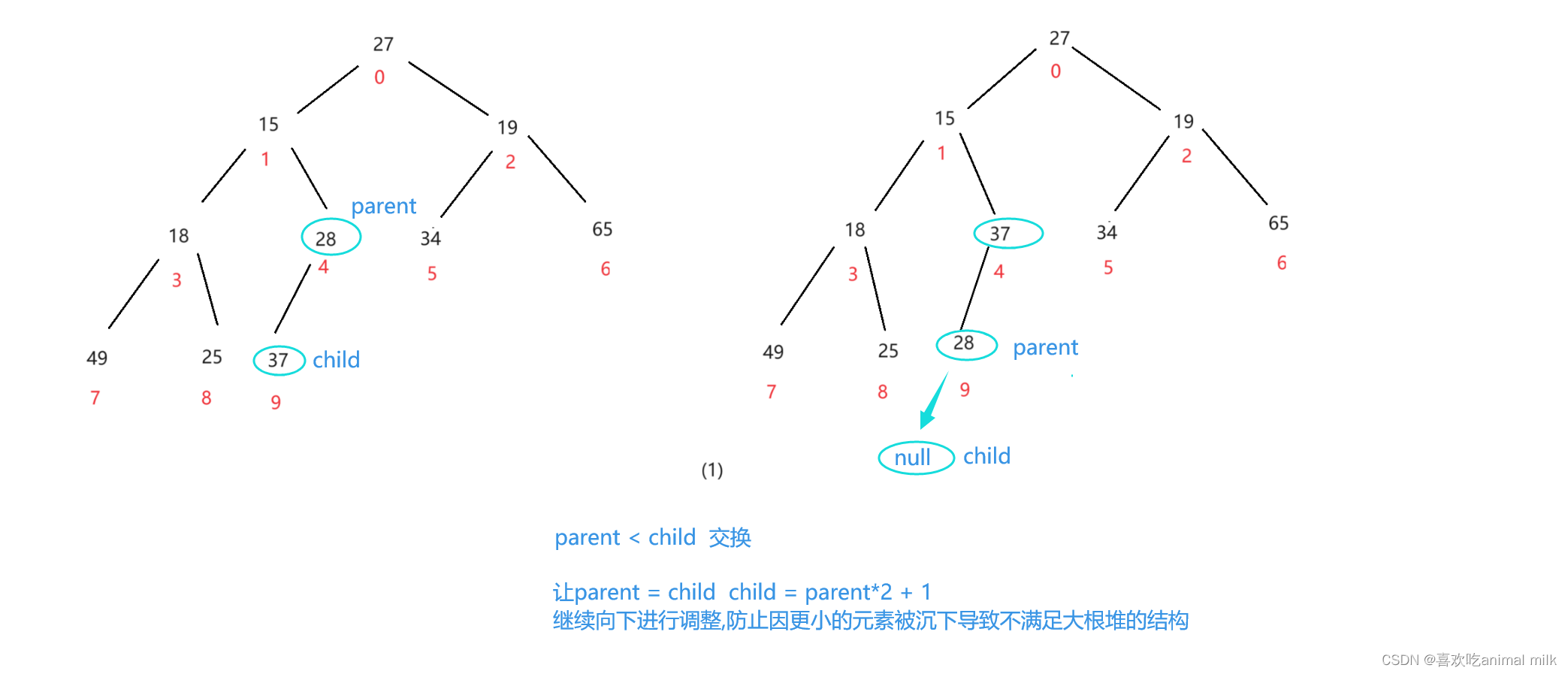

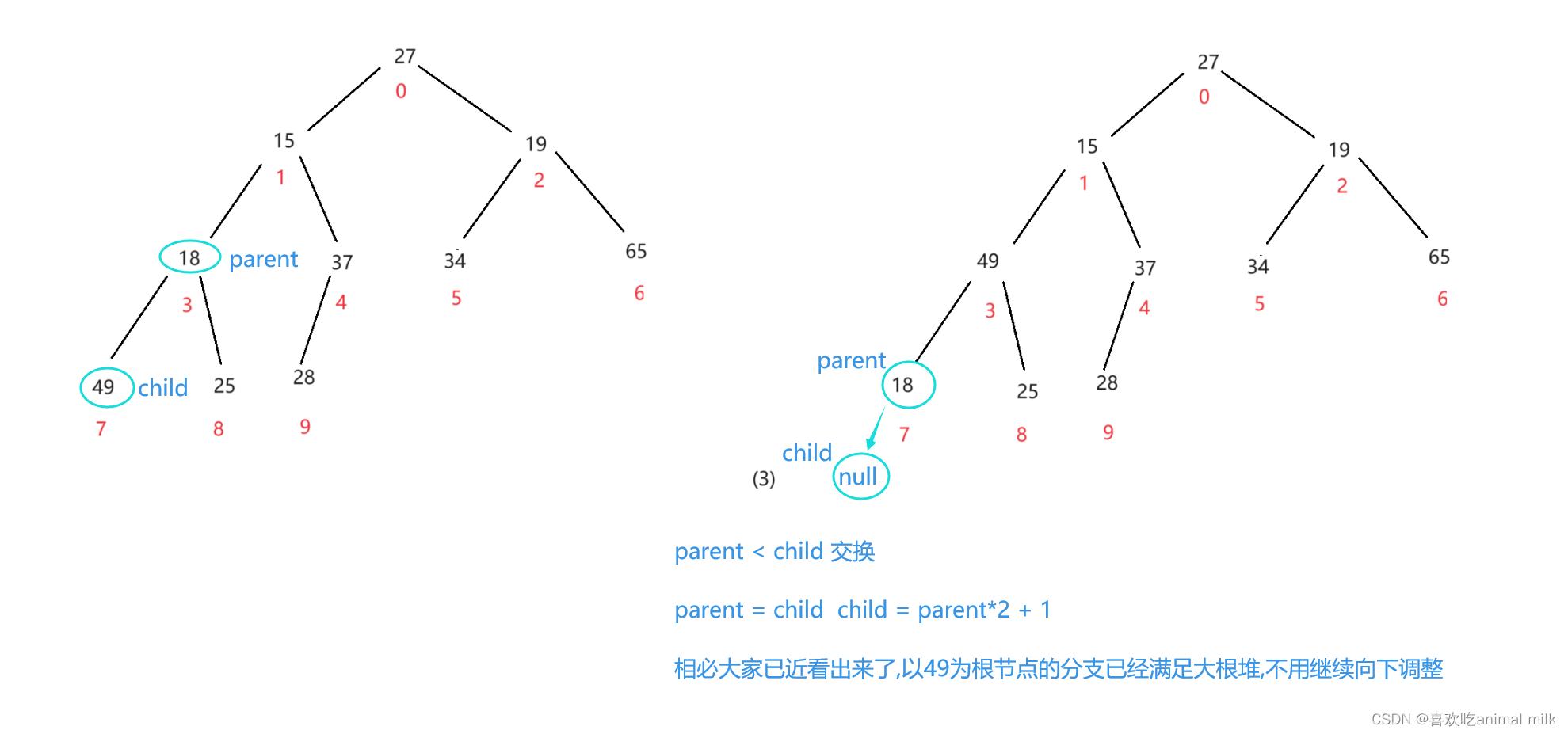
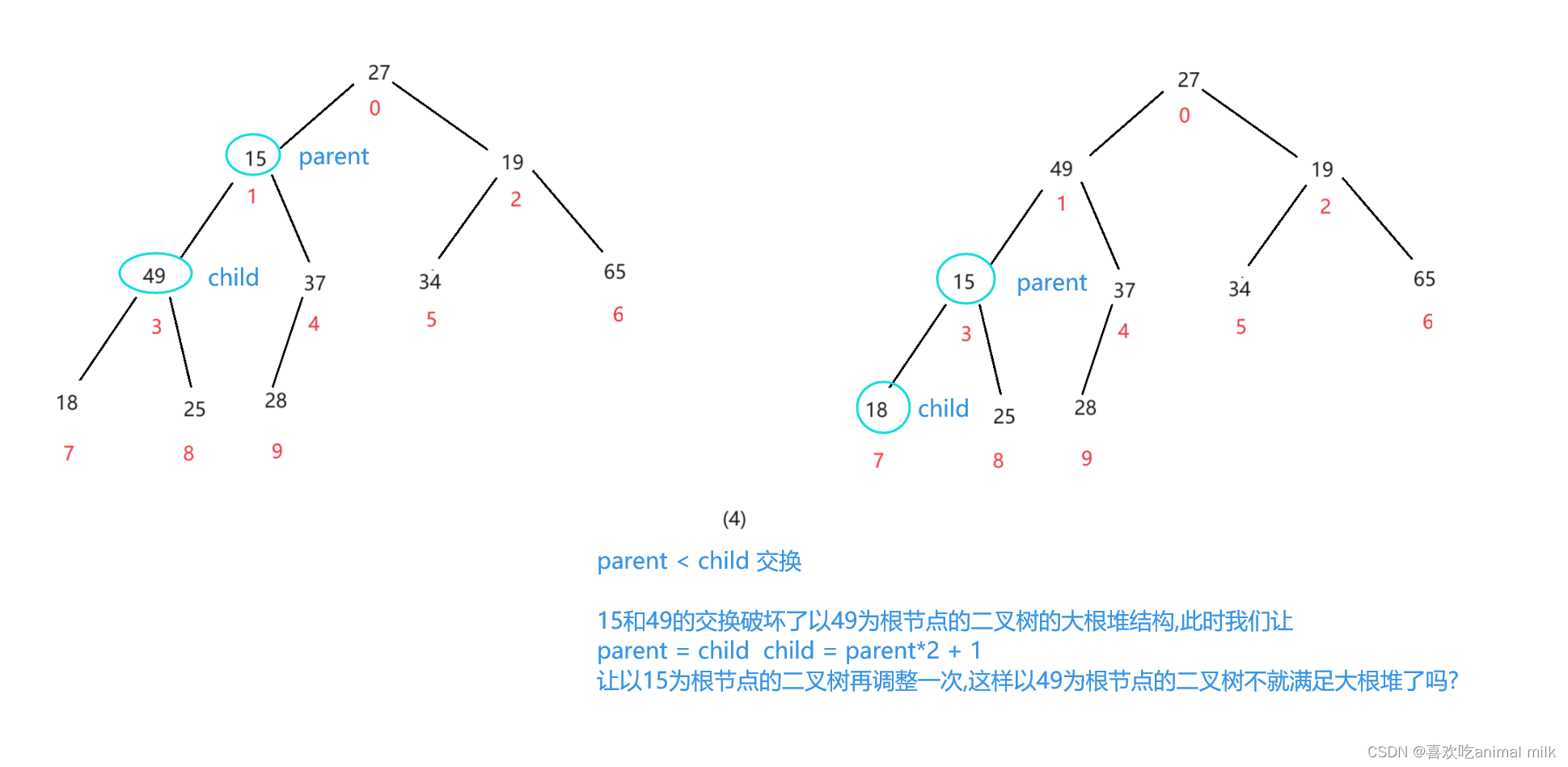
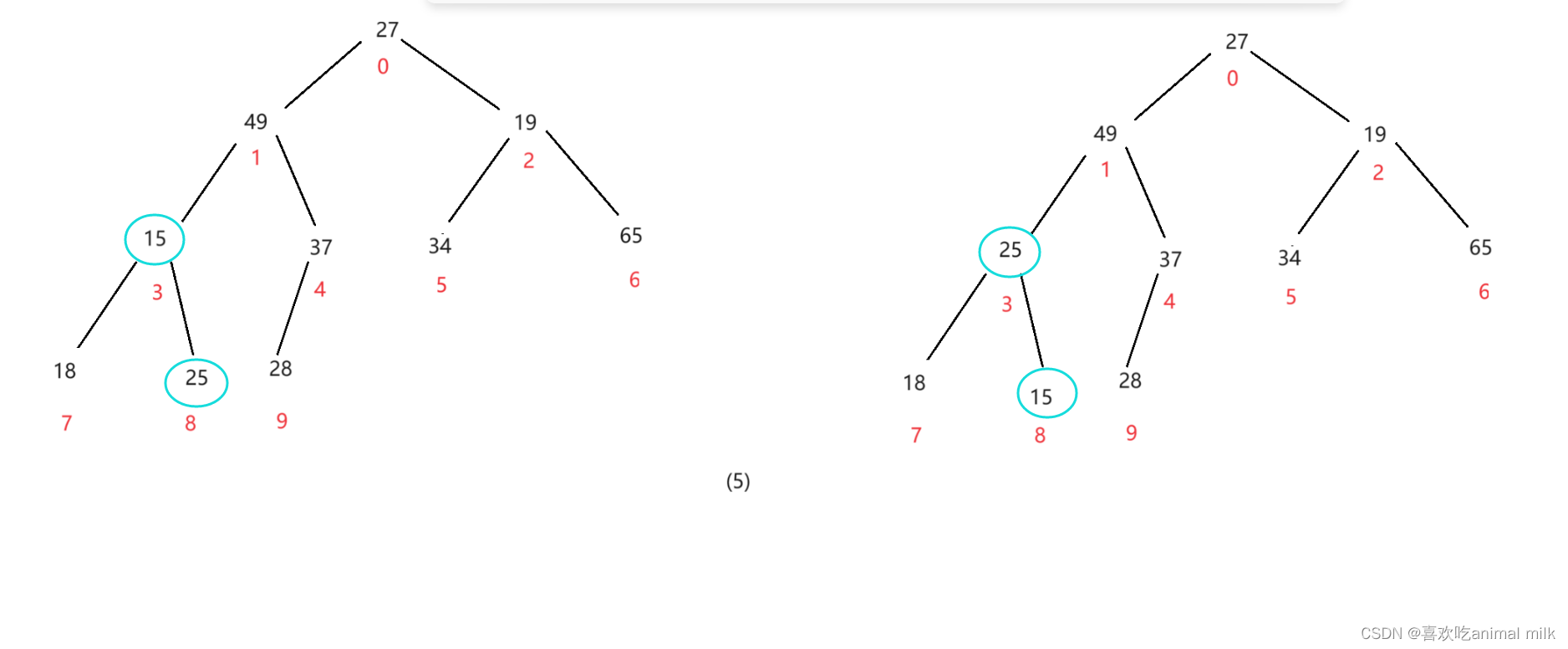
进行到这里左子树宣告调整完毕,开始进行右子树的调整
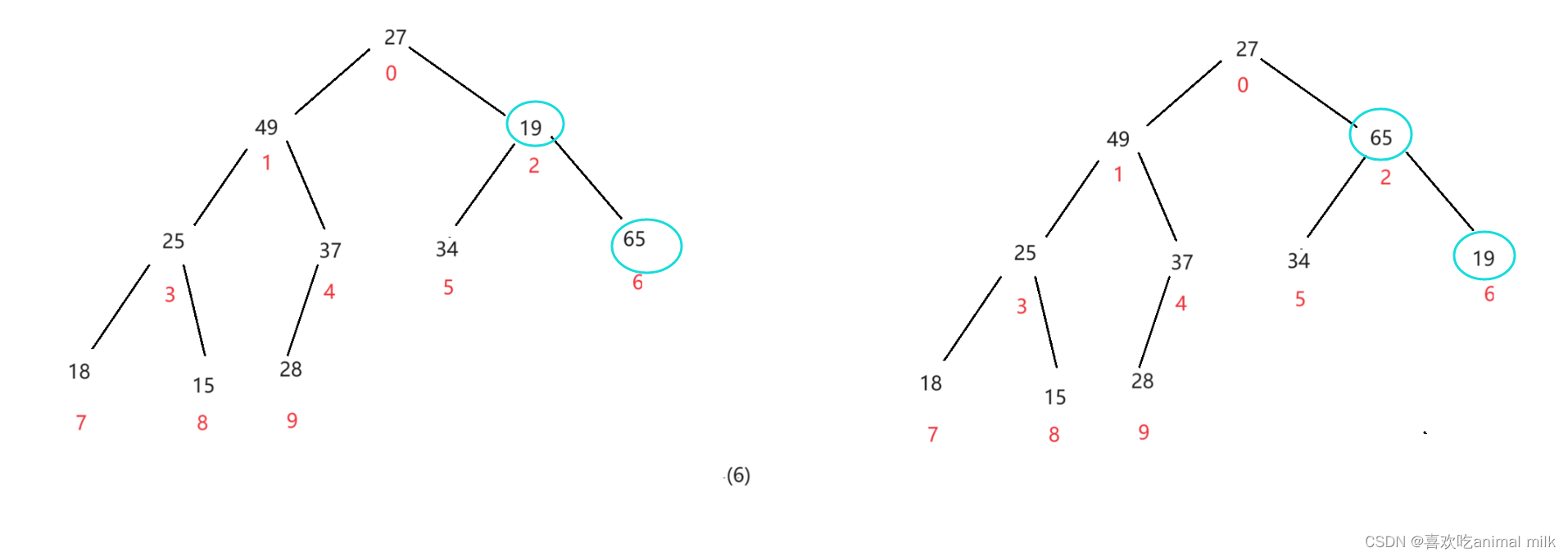
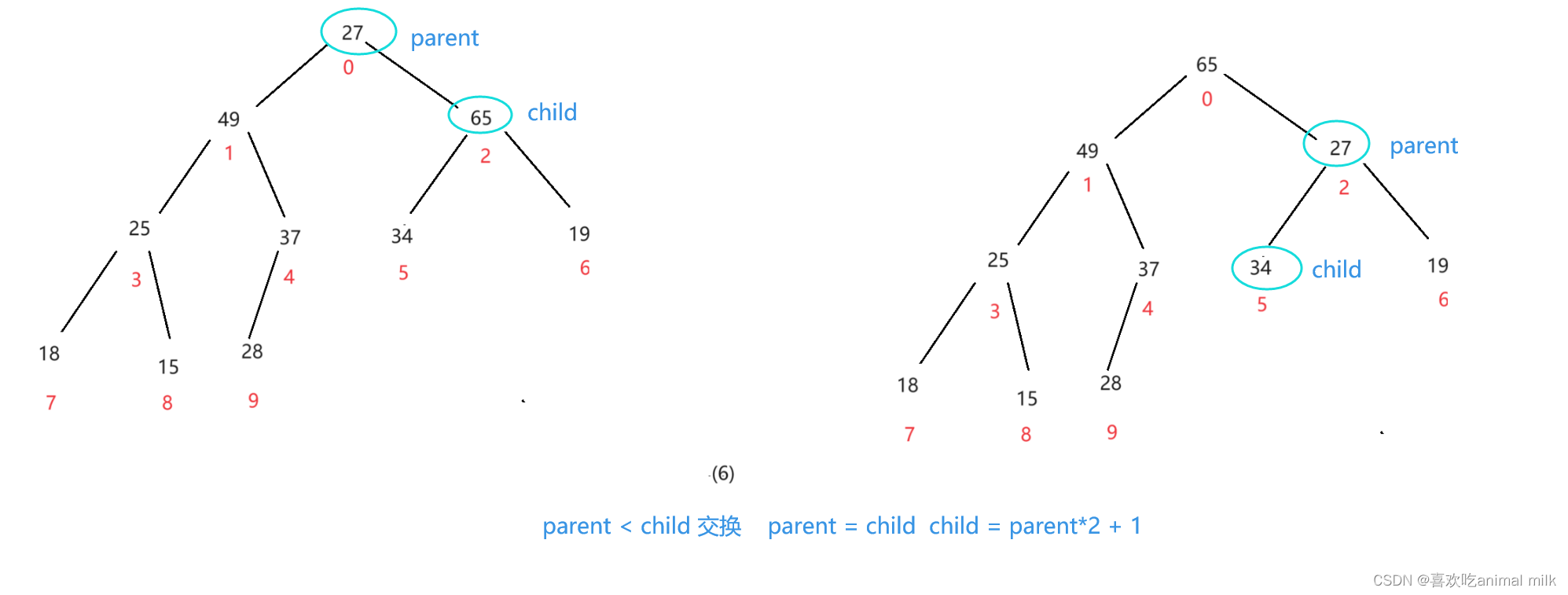
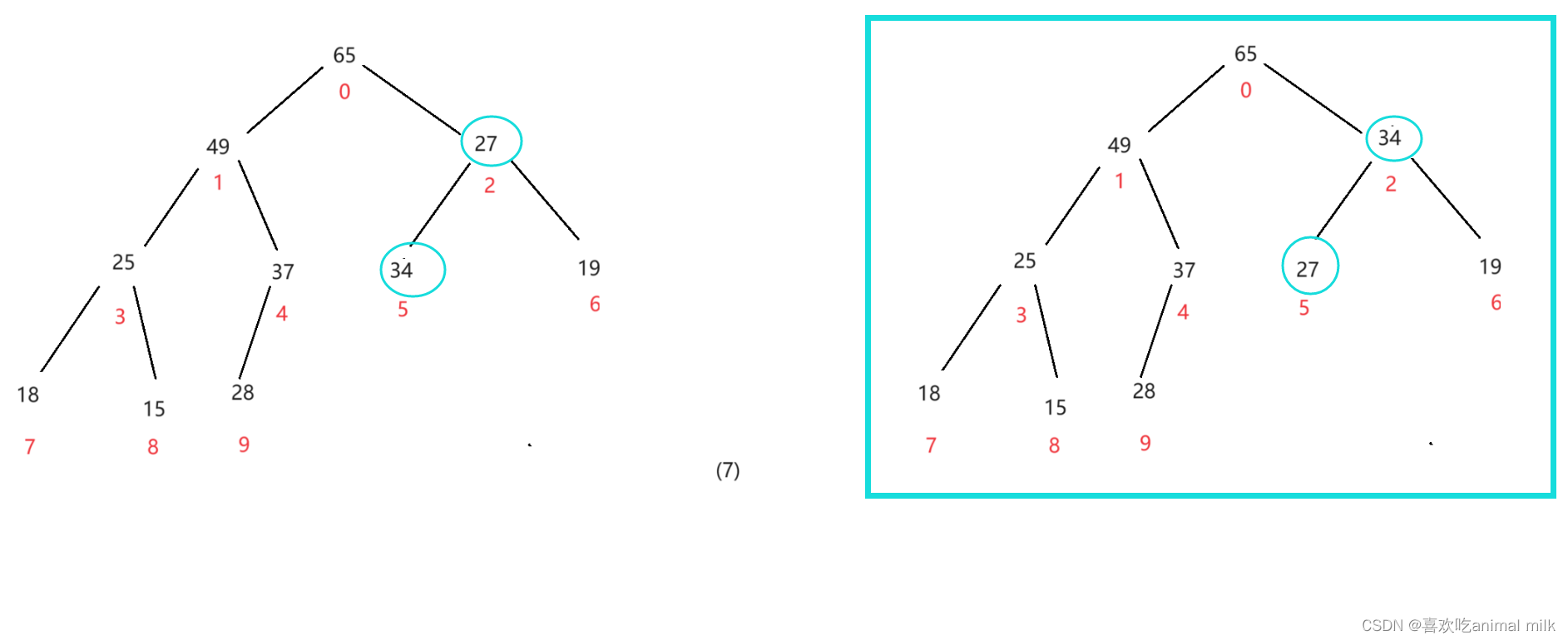 调整完毕!
调整完毕!
代码实现
private void shiftDown(int parent, int len) {int child = 2 * parent + 1;// 对交换引起的堆结构的改变进行调整(如果改变就调整)while (child < len) {// 找出左右孩子中最大的孩子,用child进行记录if (child + 1 < len && elem[child] < elem[child + 1]) {child++;}// 判断大小关系if (elem[child] > elem[parent]) {swap(child,parent);// parent中大的元素往下移动,可能会造成子树不满足堆的性质,因此需要继续向下调整parent = child;child = 2 * parent + 1;} else {// 左孩子为空,表示以最开始的parent为根的二叉树已经是大根堆结构break;}}}堆的创建
public void createHeap() {// 找倒数第一个非叶子节点,从该节点位置开始往前一直到根节点,遇到一个节点,应用向下调整for (int parent = (size - 1 - 1) / 2; parent >= 0; parent--) {shiftDown(parent, size);}}堆的删除
注意:堆的删除一定删除的是堆顶元素。具体如下:
1. 将堆顶元素对堆中最后一个元素交换
2. 将堆中有效数据个数减少一个
3. 对堆顶元素进行向下调整
public int poll(){int temp = elem[0];swap(0, size);size--;// 调整完之后需要进行先下调整,因为原来的最后一个元素变成了堆顶元素,不用想的肯定不满足大根堆的结构shiftDown(0, size);return temp;}向上调整
在最大堆中,向上调整的过程是将当前节点与其父节点进行比较,如果当前节点大于其父节点,就将它们交换位置。然后,继续向上比较和交换,直到当前节点不再大于其父节点或者已经到达根节点。
private void shiftUp(int child) {while (child != 0) {int parent = (child - 1) / 2;if (elem[parent] < elem[child]) {swap(child,parent);child = parent;} else {break;}}}堆的插入
堆的插入总共需要两个步骤:
1. 先将元素放入到底层空间中(注意:空间不够时需要扩容)
2. 将最后新插入的节点向上调整,直到满足堆的性质
小根堆中插入10

public void offer(int val) {if (isFull()) {this.elem = Arrays.copyOf(this.elem, 2 * this.elem.length);}elem[size] = val;shiftUp(size);size++;}总代码
public class BigHeap {int[] elem;int size;public BigHeap(int capacity) {elem = new int[capacity];}public void initHeap(int[] arr) {for (int i = 0; i < arr.length; i++) {elem[i] = arr[i];size++;}}public void createHeap() {for (int parent = (size - 1 - 1) / 2; parent >= 0; parent--) {shiftDown(parent, size);}}public int poll(){int temp = elem[0];swap(0, size);size--;// 调整完之后需要进行先下调整,因为原来的最后一个元素变成了堆顶元素,不用想的肯定不满足大根堆的结构shiftDown(0, size);return temp;}private void shiftDown(int parent, int len) {int child = 2 * parent + 1;// 对交换引起的堆结构的改变进行调整(如果改变就调整)while (child < len) {// 找出左右孩子中最大的孩子,用child进行记录if (child + 1 < len && elem[child] < elem[child + 1]) {child++;}// 判断大小关系if (elem[child] > elem[parent]) {swap(child,parent);// parent中大的元素往下移动,可能会造成子树不满足堆的性质,因此需要继续向下调整parent = child;child = 2 * parent + 1;} else {// 左孩子为空,表示以最开始的parent为根的二叉树已经是大根堆结构break;}}}public void offer(int val) {if (isFull()) {this.elem = Arrays.copyOf(this.elem, 2 * this.elem.length);}elem[size] = val;shiftUp(size);size++;}private void shiftUp(int child) {while (child != 0) {int parent = (child - 1) / 2;if (elem[parent] < elem[child]) {swap(child,parent);child = parent;} else {break;}}}public boolean isFull() {return elem.length == size;}public void swap(int i,int j){int temp = elem[i];elem[i] = elem[j];elem[j] = temp;}
}三 . 优先级队列
前面介绍过队列,队列是一种先进先出(FIFO)的数据结构,但有些情况下,操作的数据可能带有优先级,一般出队 列时,可能需要优先级高的元素先出队列,该中场景下,使用队列显然不合适,比如:在手机上玩游戏的时候,如果有来电,那么系统应该优先处理打进来的电话;初中那会班主任排座位时可能会让成绩好的同学先挑座位。 在这种情况下,数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数 据结构就是优先级队列(Priority Queue)。
优先级队列可以用于很多场景,例如任务调度、进程调度、事件处理等。在任务调度中,可以根据任务的优先级来决定先执行哪些任务;在进程调度中,可以根据进程的优先级来决定先执行哪些进程;在事件处理中,可以根据事件的优先级来决定先处理哪些事件。
在实际应用中,优先级队列可以通过使用堆来实现,因为堆具有良好的时间复杂度和空间复杂度。通过使用堆来实现优先级队列,可以在log₂ n的时间复杂度内插入和删除元素,以及在O(1)的时间复杂度内获取优先级最高的元素。
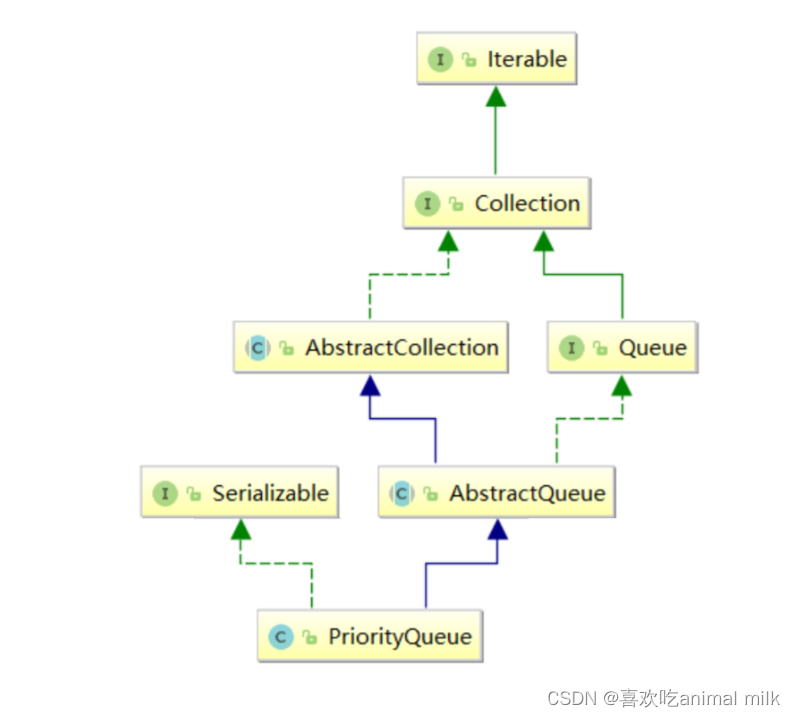
注意点:
1. 使用时必须导入PriorityQueue所在的包
2. PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出 ClassCastException异常
3. 不能插入null对象,否则会抛出NullPointerException
4. 没有容量限制,可以插入任意多个元素,其内部可以自动扩容
5. 插入和删除元素的时间复杂度为O(log₂ n)
6. PriorityQueue底层使用了堆数据结构
7. PriorityQueue默认情况下是小堆---即每次获取到的元素都是最小的元素
堆模拟实现优先级队列
class MyPriorityQueue {// 演示作用,不再考虑扩容部分的代码private int[] array = new int[100];private int size = 0;public void offer(int e) {array[size++] = e;shiftUp(size - 1);}public int poll() {int oldValue = array[0];array[0] = array[size--];shiftDown((size-1-1)/2,size);return oldValue;}public int peek() {return array[0];}}总结
这篇文章给大家重点讲解了堆的模拟实现还有其应用之一 优先级队列,大家好好理解,我们下一篇博客见。
相关文章:

数据结构-优先级队列(堆)
文章目录 目录 文章目录 前言 一 . 堆 二 . 堆的创建(以大根堆为例) 堆的向下调整(重难点) 堆的创建 堆的删除 向上调整 堆的插入 三 . 优先级队列 总结 前言 大家好,今天给大家讲解一下堆这个数据结构和它的实现 - 优先级队列 一 . 堆 堆(Heap࿰…...
C++11新特性(语法糖,新容器)
距离C11版本发布已经过去那么多年了,为什么还称为新特性呢?因为笔者前面探讨的内容,除了auto,范围for这些常用的,基本上是用着C98的内容,虽说C11已经发布很多年,却是目前被使用最广泛的版本。因…...
开机可用内存分析Tip
一、开机内存简介 开机内存指的是开机一段时间稳定后的可用内存。一般项目都会挑选同平台其他优秀竞品内存数据,这个也是衡量性能的一个重要标准。所以要进行开机内存检测,同时优化非法内存进程占用。 二、测试前期核查任务 开机内存测试前要进行测试机…...

【Python基础】4. 基本语句
文章目录 注释(Comment)解释伴随行文本编码问题 输入输出语句(Input & Output)输出语句普通输出格式化输出(3种)format 格式总结 输入语句 基本语句if 语句match 语句(Python3.10 新增&…...

兼顾友好与安全,隐私协议 Unijoin 助推新一轮 Web3 浪潮
区块链本身不仅崇尚去中心化,同时也崇尚公开透明,虽然这正在让 DAO 治理等变得更加公平,但它同时也是一把双刃剑,个人交易者尤其是一些巨鲸交易者的所以链上交易都被公之于众,这似乎并不是他们想要的结果。 所以从加密…...
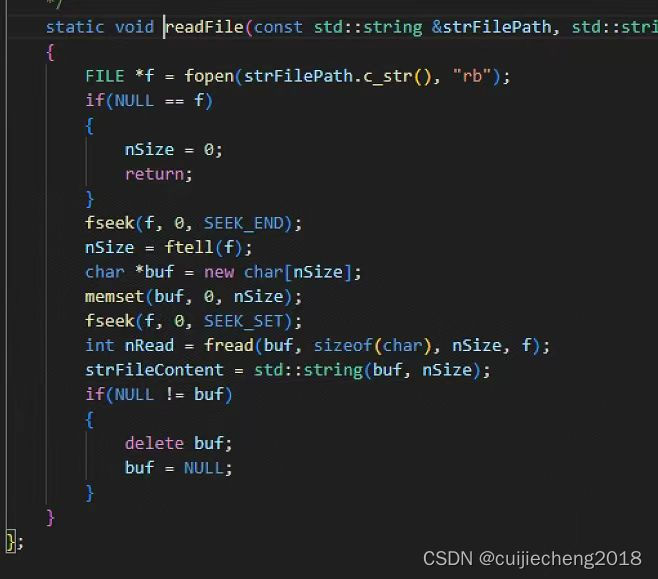
TCP端口崩溃,msg:socket(): Too many open files
一、现象 linux系统中运行了一个TCP服务器,该服务器监听的TCP端口为10000。但是长时间运行时发现该端口会崩溃,TCP客户端连接该端口会失败: 可以看到进行三次握手时,TCP客户端向该TCP服务器的10000端口发送了SYN报文,…...
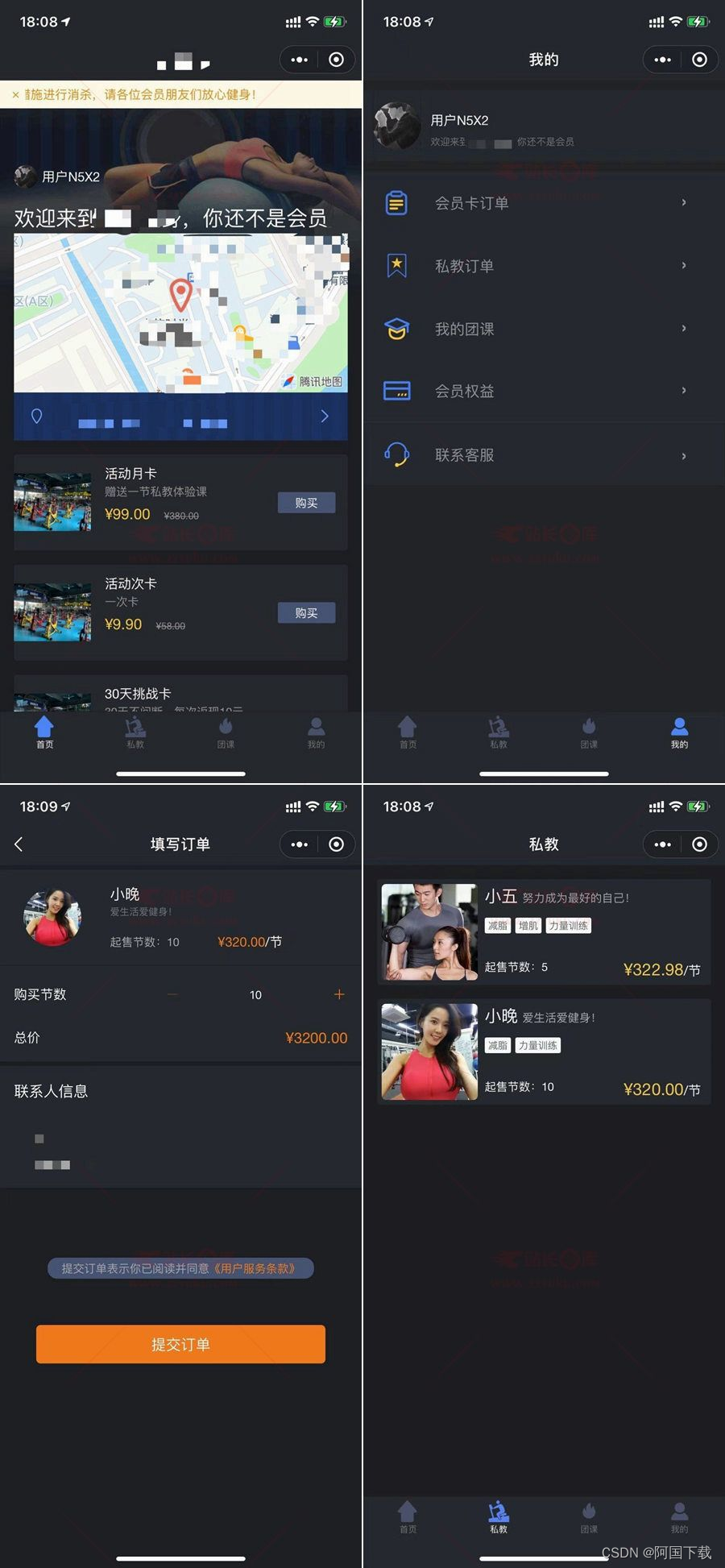
基于Laravel 5.6的运动健身类小程序前后端源码
基于Laravel 5.6的运动健身、健康类小程序前后端源码,一套比较基础的运动健康、健身类小程序源码。朋友自己无聊写的,比较基础,有需要的可以拿去修修改改升级开发一下。 使用宝塔安装,比较省事,PHP相关的扩展需要启用…...
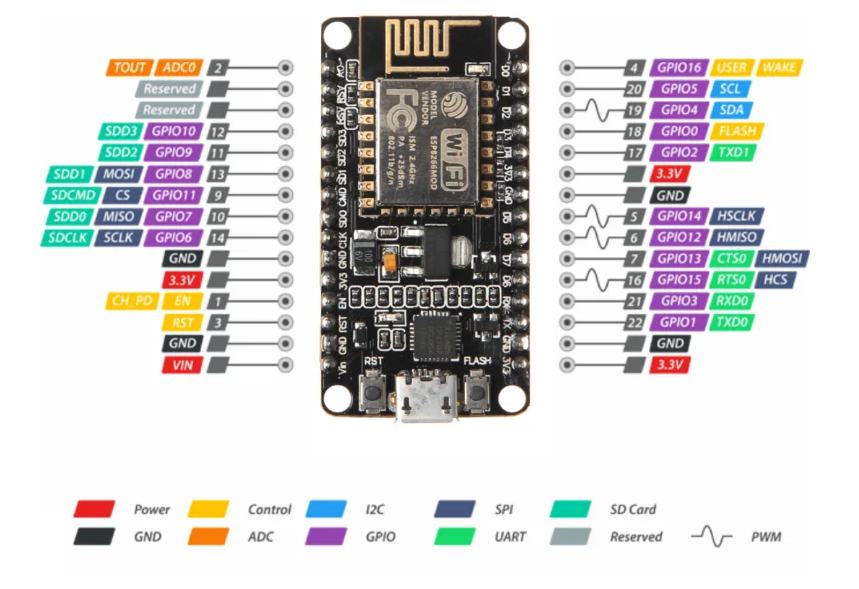
NodeMCU ESP8266硬件开发板的熟悉
文章目录 硬件开发环境的熟悉基础介绍什么是 ESP8266 NodeMCU?NodeMCU芯片ESP12-E 模组开发板 ESP8266 版本引脚图Power GND I2CGPIOADCUARTSPIPWMControl 总结 硬件开发环境的熟悉 基础介绍 什么是 ESP8266 NodeMCU? ESP8266是乐鑫开发的一款低成本 …...
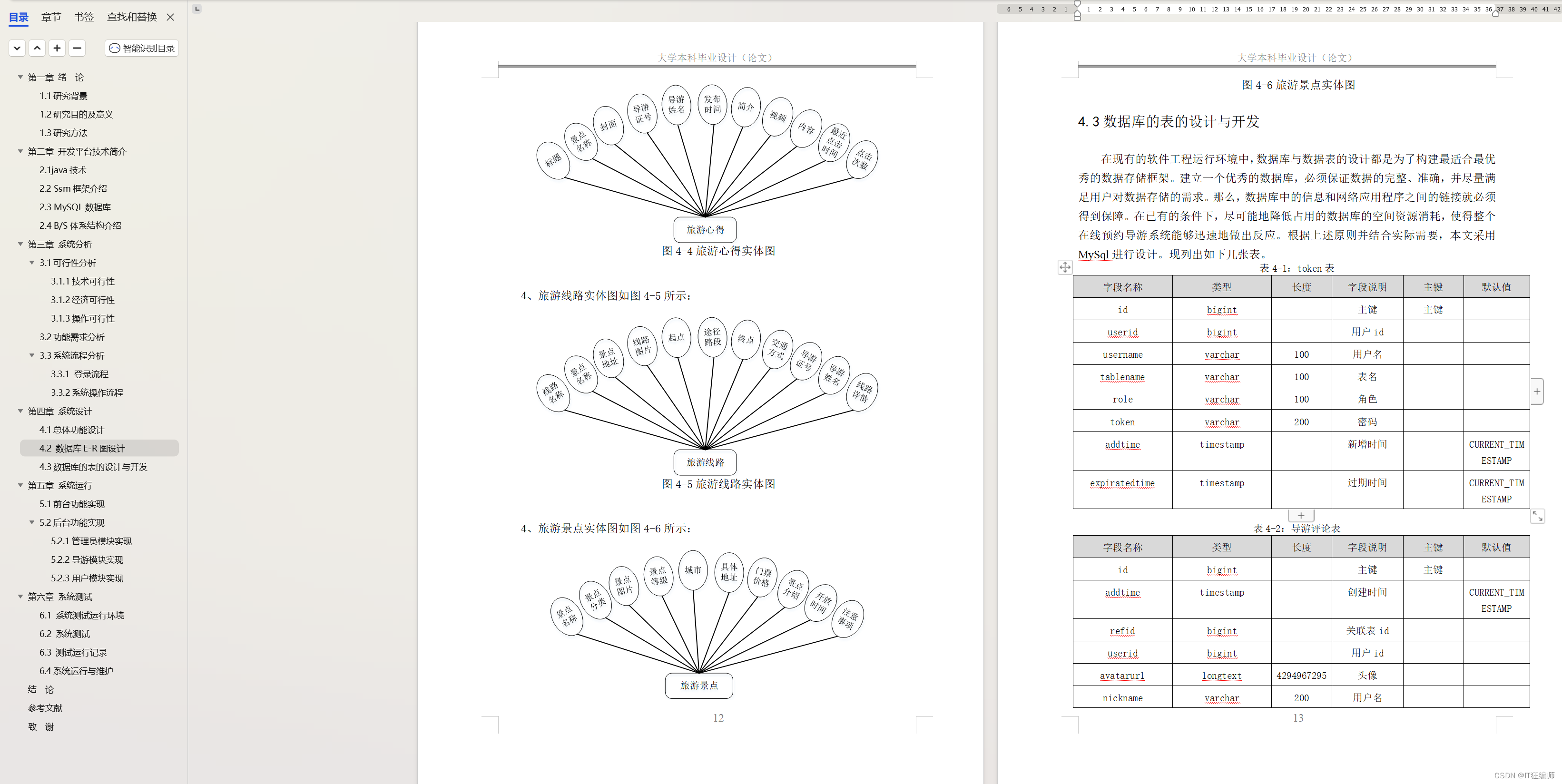
计算机毕业设计 基于SSM的在线预约导游系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...
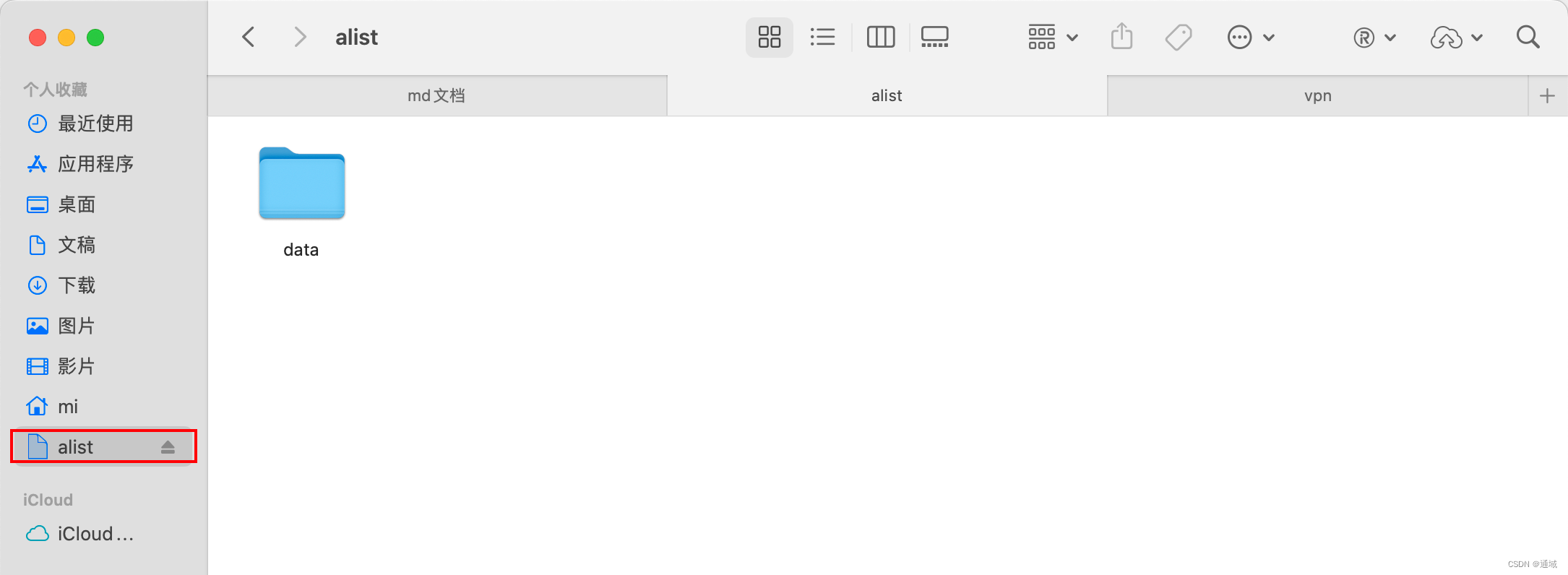
Mac 挂载 Alist网盘
挂载服务器的Alist 网盘到 Mac mac,使用的是 CloundMounter 这个软件进行挂载 http://ip:port/dav/ 需要在末尾加上 /dav/ 在一些服务器上,为了提供WebDAV服务,需要在URL地址的末尾添加"/dav/“。这是因为WebDAV协议规定了一些标准的URL路径&#x…...
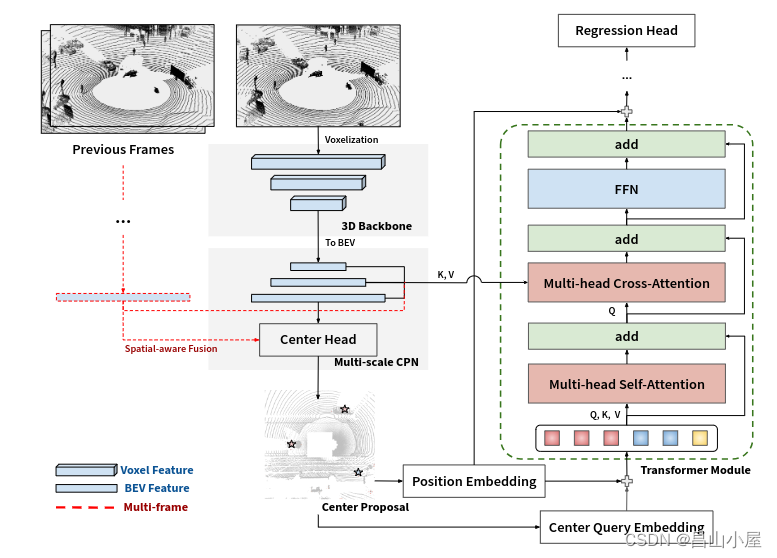
【多模态融合】TransFusion学习笔记(1)
工作上主要还是以纯lidar的算法开发,部署以及系统架构设计为主。对于多模态融合(这里主要是只指Lidar和Camer的融合)这方面研究甚少。最近借助和朋友们讨论论文的契机接触了一下这方面的知识,起步是晚了一点,但好歹是开了个头。下面就借助TransFusion论文…...

(二)正点原子STM32MP135移植——TF-A移植
目录 一、TF-A概述 二、编译官方代码 2.1 解压源码 2.2 打补丁 2.3 编译准备 (1)修改Makfile.sdk (2)设置环境变量 (3)编译 三、移植 3.1 复制官方文件 3.2 修改电源 3.3 修改TF卡和emmc 3.4 添…...
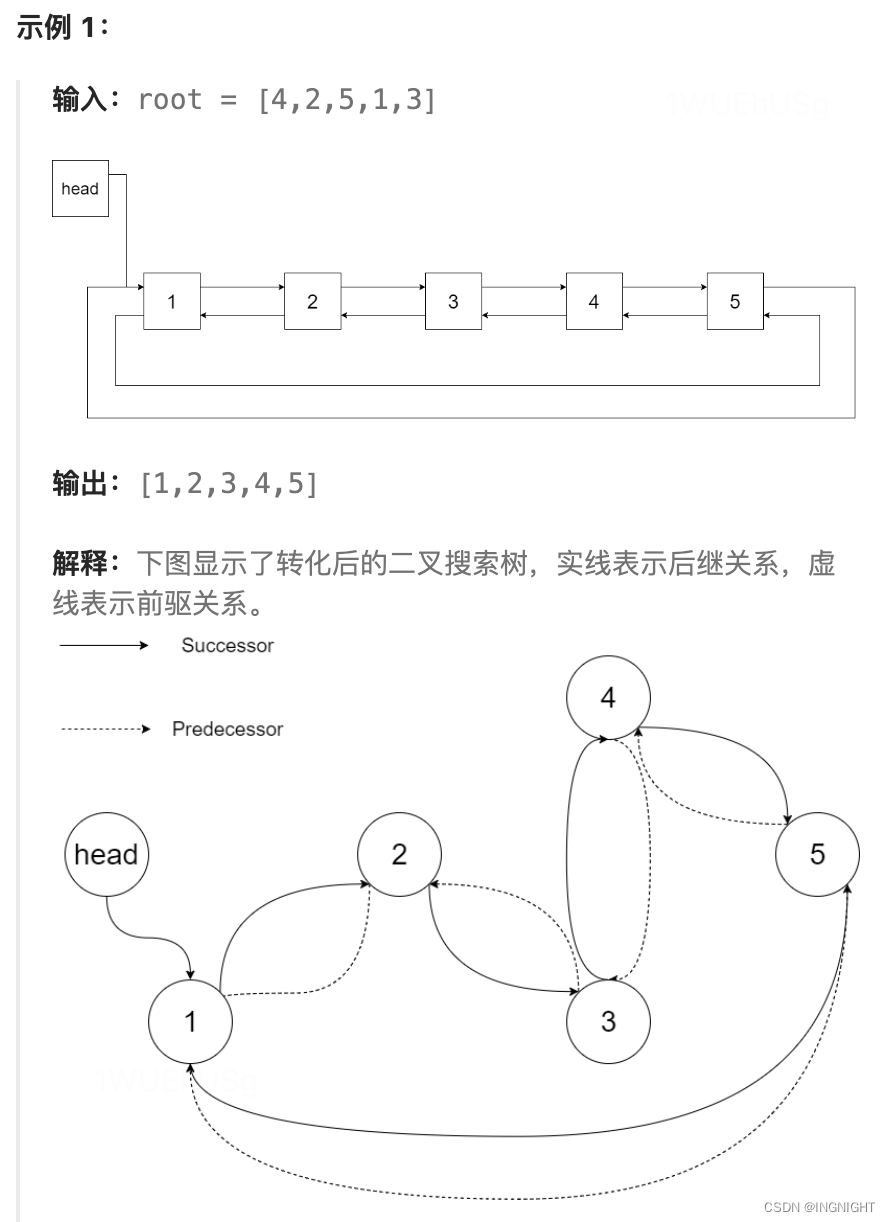
将二叉搜索树转化为排序的双向链表
链接: LCR 155. 将二叉搜索树转化为排序的双向链表 题解: /* // Definition for a Node. class Node { public:int val;Node* left;Node* right;Node() {}Node(int _val) {val _val;left NULL;right NULL;}Node(int _val, Node* _left…...
电脑dll丢失应该怎么解决,dll文件丢失怎么恢复方法分享
DLL(Dynamic Link Library,动态链接库)是一种可执行文件,它包含了在程序运行时需要调用的代码和资源。DLL 文件的主要作用是实现代码和资源的共享,这样在多个程序之间就可以避免重复的代码和资源,从而节省系…...

通达信和同花顺能否实现程序化自动交易股票,量化交易如何实现?
以下写给正在寻找自动交易接口的朋友,首先,不是那种设置个简单条件的条件单,或者某些客户端上形同鸡肋的策略交易,那些策略根本称不上策略,还有各种限制,不支持这个不支持那个,可设置的参数也不…...
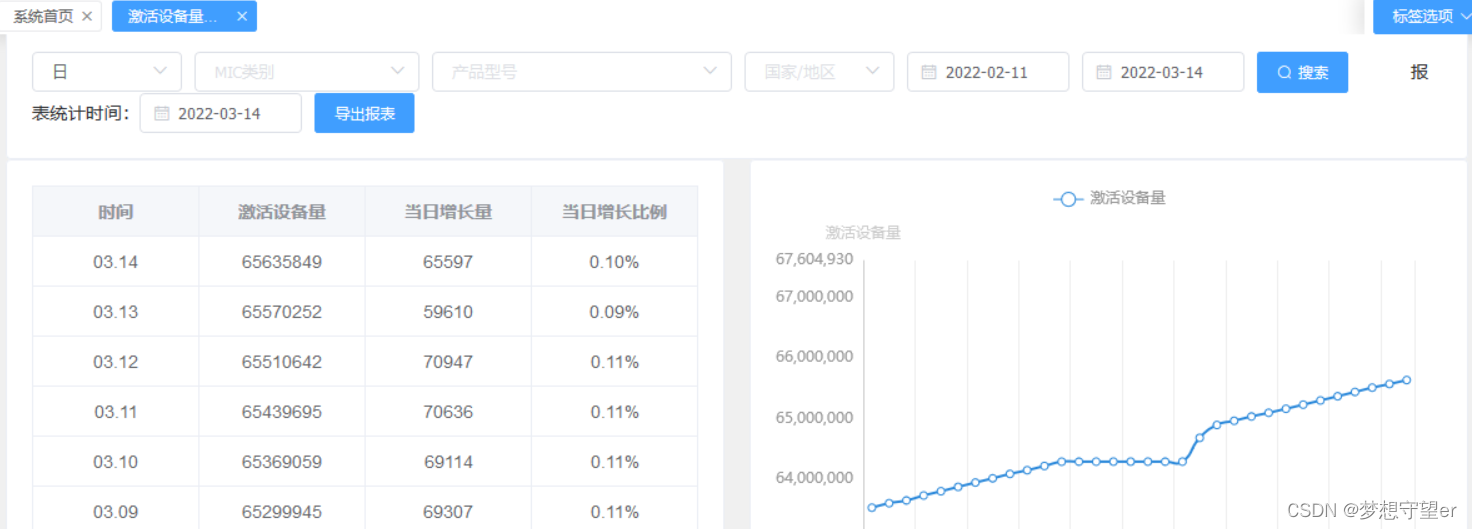
基于Kylin的数据统计分析平台架构设计与实现
目录 1 前言 2 关键模块 2.1 数据仓库的搭建 2.2 ETL 2.3 Kylin数据分析系统 2.4 数据可视化系统 2.5 报表模块 3 最终成果 4 遇到问题 1 前言 这是在TP-LINK公司云平台部门做的一个项目,总体包括云上数据统计平台的架构设计和组件开发,在此只做…...

Linux CentOS7 vim寄存器
计算机中通常所说的寄存器Register一般指的是CPU中的寄存器,用来暂存CPU处理所需要的指令、数据等。 vim中同样也有寄存器,使用的方式和CPU非常类似。 vim中的寄存器(register)作用和windows中的剪切板类似,不过vim中的寄存器不止一个&…...
摄影后期图像编辑软件Lightroom Classic 2023 mac中文特点介绍
Lightroom Classic 2023 mac是一款图像处理软件,是数字摄影后期制作的重要工具之一,lrc2023 mac适合数字摄影后期制作、摄影师、设计师等专业人士使用。 Lightroom Classic 2023 mac软件特点 高效的图像管理:Lightroom Classic提供了强大的图…...
一种4g扫码付费通电控制器方案
之前开发了一款扫码付款通电控制器 功能:用户扫码付款后设备通电,开始倒计时,倒计时结束后设备断电,资金到账商家的商家助手里面,腾讯会收取千分之6手续费。 产品主要应用场景 本产品主要应用于各类无人值守或者自助…...

桌面自动化工具总结
引言:产品经理提出桌面程序需要自动化的测试,避免繁琐的人肉点击。说干就干。 现有自动化工具是五花八门,我找了两个框架。 这两个框架都是基于微软的UIA 框架,链接地址 https://learn.microsoft.com/en-us/windows/win32/winauto/uiauto-providerportal?source=recommen…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
