矩阵的c++实现(2)
上一次我们了解了矩阵的运算和如何使用矩阵解决斐波那契数列,这一次我们多看看例题,了解什么情况下用矩阵比较合适。
先看例题
1.洛谷P1939 【模板】矩阵加速(数列)
模板题应该很简单。

补:1<n<=10^9
10^9肯定超了,所以可以用矩阵做
我们可以观察到,每一项(x>3)都是由两个量组成,于是创建矩阵:
同时:
那么因为如果要再让,A*base 之后还是应该是前一个为一项,后一项为它的两项前。所以?处应为
。??处应为什么自己想想,发在评论区里吧。
但是,在A中并没有出现,这样我们就不可以用A*base表示B了,因为矩阵的乘法中,必须要上一个矩阵中有的元素,才能进入下一个矩阵中。
无论怎样,都无法表示为
的形式,所以B不可以由A构成。
那这个时候就可以用一个巧妙的方法:我们在A和B中都增加这一项,这样就会变成
可以表示为
,这样就可以满足每一个条件都可以了。
那么我们利用矩阵乘法,在纸上演算七七四十八个小时,就可以得出,
那么用和斐波那契数列一样的做法,快速幂即可
#include<bits/stdc++.h>
using namespace std;
#define mod 1000000007
struct Matrix{int n,m;long long a[100][100];Matrix(){memset(a,0,sizeof(a));}Matrix(int _n,int _m){n=_n;m=_m;memset(a,0,sizeof(a));}
};
Matrix ans(1,3);
Matrix base(3,3);
void init(){ans.a[0][0]=1;ans.a[0][1]=1;ans.a[0][2]=1;base.a[0][0]=1;base.a[0][1]=1;base.a[0][2]=0;base.a[1][0]=0;base.a[1][1]=0;base.a[1][2]=1;base.a[2][0]=1;base.a[2][1]=0;base.a[2][2]=0;
}
Matrix mul(Matrix a,Matrix b){Matrix res(a.n,b.m);for(int i=0;i<a.n;i++){for(int j=0;j<b.m;j++){for(int k=0;k<a.m;k++){res.a[i][j]+=a.a[i][k]*b.a[k][j]%mod;}res.a[i][j]%=mod;}}return res;
}
Matrix bpow(Matrix a,long long n){Matrix res(a.n,a.n);for(int i=0;i<a.n;i++)res.a[i][i]=1;while(n!=0){if(n&1){res=mul(res,a);}a=mul(a,a);n>>=1;}return res;
}
long long F(long long n){base=bpow(base,n-3);/*for(int i=0;i<3;i++){for(int j=0;j<3;j++){cout<<base.a[i][j];}cout<<endl;}*/ans=mul(ans,base);return ans.a[0][0]%mod;
}
int main(){long long t;cin>>t;while(t--){long long n;cin>>n;if(n<=3){cout<<1<<endl;continue;}init();cout<<F(n)<<endl;}return 0;
}
2.洛谷P1349 广义斐波那契数列

其实很简单,就是把斐波那契数列的模板套一下
先写一半
相关文章:

矩阵的c++实现(2)
上一次我们了解了矩阵的运算和如何使用矩阵解决斐波那契数列,这一次我们多看看例题,了解什么情况下用矩阵比较合适。 先看例题 1.洛谷P1939 【模板】矩阵加速(数列) 模板题应该很简单。 补:1<n<10^9 10^9肯定…...

RPC 框架之Thrift入门(一)
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...
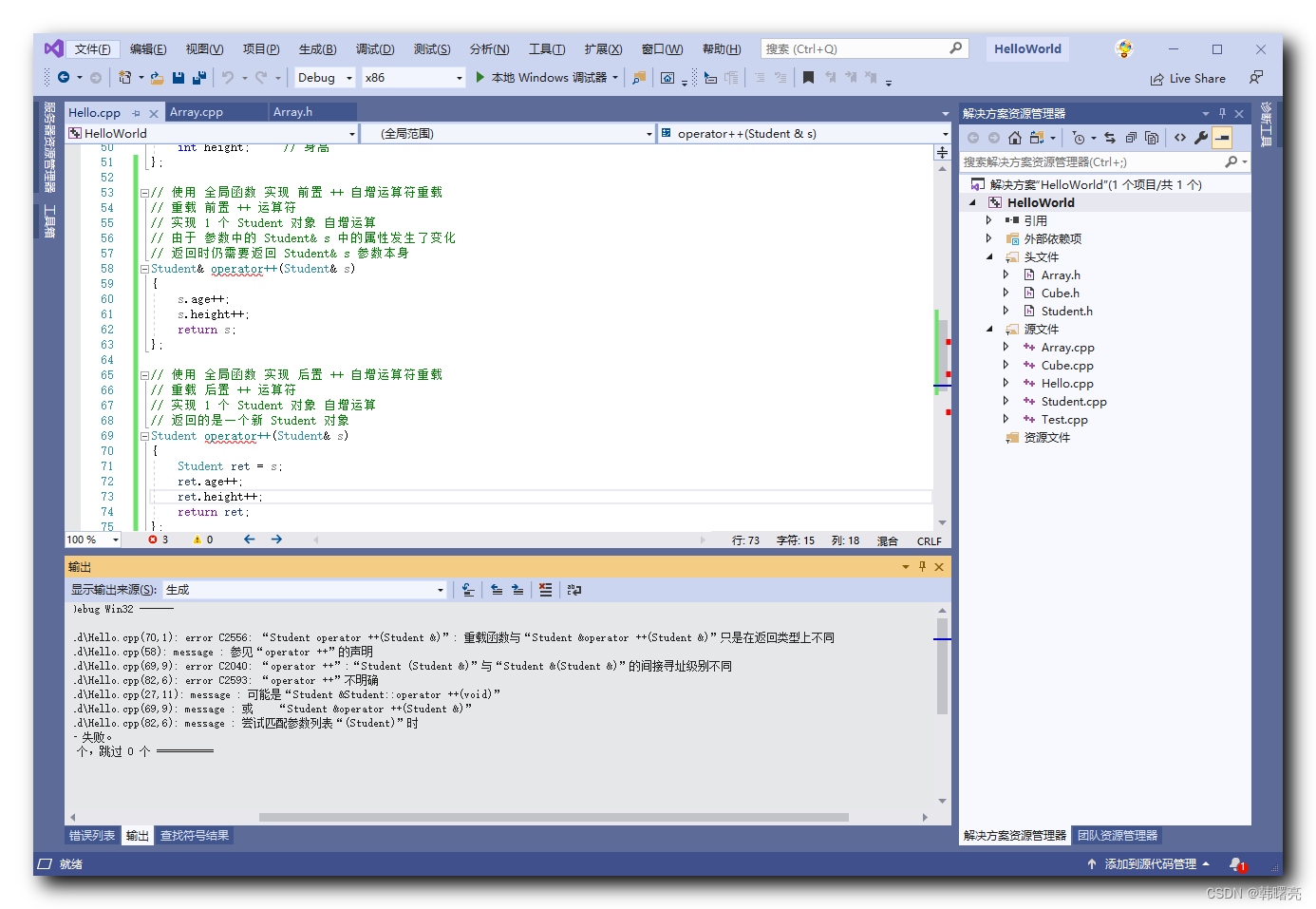
【C++】运算符重载 ⑥ ( 一元运算符重载 | 后置运算符重载 | 前置运算符重载 与 后置运算符重载 的区别 | 后置运算符重载添加 int 占位参数 )
文章目录 一、后置运算符重载1、前置运算符重载 与 后置运算符重载 的区别2、后置运算符重载添加 int 占位参数 上 2 2 2 篇博客 【C】运算符重载 ④ ( 一元运算符重载 | 使用 全局函数 实现 前置 自增运算符重载 | 使用 全局函数 实现 前置 - - 自减运算符重载 )【C】运算符…...

538. 把二叉搜索树转换为累加树
题目描述 给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。 提醒一下,二叉搜索树满足下列约束…...

java8日期时间工具类
【README】 1)本文总结了java8中日期时间常用工具方法;包括: 日期时间对象格式化为字符串;日期时间字符串解析为日期时间对象;日期时间对象转换; 转换过程中,需要注意的是: Instan…...

算法-动态规划/trie树-单词拆分
算法-动态规划/trie树-单词拆分 1 题目概述 1.1 题目出处 https://leetcode.cn/problems/word-break/description/?envTypestudy-plan-v2&envIdtop-interview-150 1.2 题目描述 2 动态规划 2.1 解题思路 dp[i]表示[0, i)字符串可否构建那么dp[i]可构建的条件是&…...

React框架核心原理
一、整体架构 三大核心库与对应的组件 history -> react-router -> react-router-dom react-router 可视为react-router-dom 的核心,里面封装了<Router>,<Route>,<Switch>等核心组件,实现了从路由的改变到组件的更新…...

python-pytorch 利用pytorch对堆叠自编码器进行训练和验证
利用pytorch对堆叠自编码器进行训练和验证 一、数据生成二、定义自编码器模型三、训练函数四、训练堆叠自编码器五、将已训练的自编码器级联六、微调整个堆叠自编码器 一、数据生成 随机生成一些数据来模拟训练和验证数据集: import torch# 随机生成数据 n_sample…...
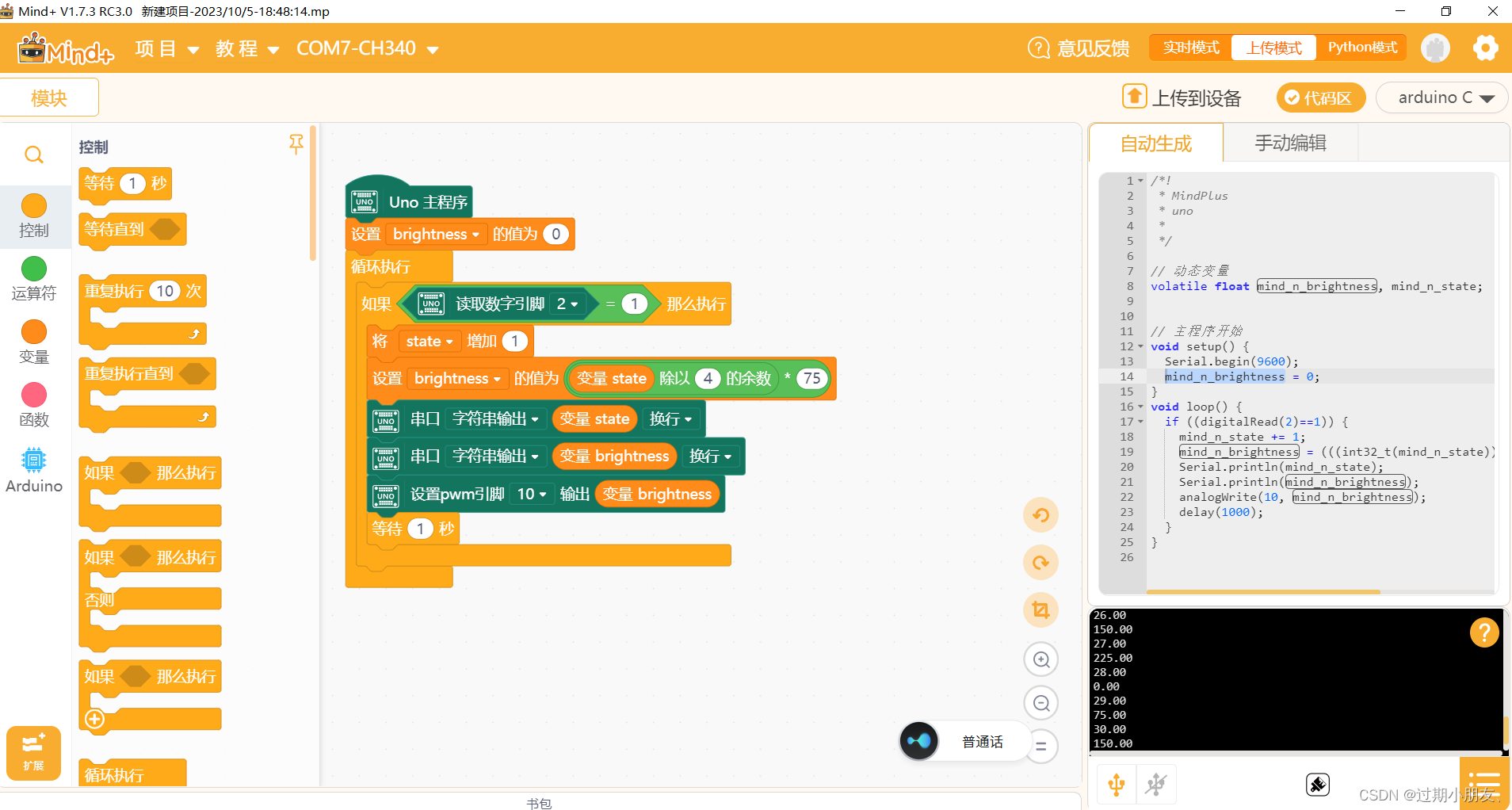
制作 3 档可调灯程序编写
PWM 0~255 可以将数据映射到0 75 150 225 尽可能均匀电压间隔...

源码分享-M3U8数据流ts的AES-128解密并合并---GoLang实现
之前使用C语言实现了一次,见M3U8数据流ts的AES-128解密并合并。 学习了Go语言后,又用Go重新实现了一遍。源码如下,无第三方库依赖。 package mainimport ("crypto/aes""crypto/cipher""encoding/binary"&quo…...

CSDN Q: “这段代码算是在STC89C52RC51单片机上完成PWM呼吸灯了吗?“
这是 CSDN上的一个问题 这段代码算是在STC89C52RC51单片机上完成PWM呼吸灯了吗,还是说得用上定时器和中断函数#include <regx52.h> 我个人认为: 效果上来说, 是的! 码以 以Time / 100-Time 调 Duty, 而 for i loop成 Period, 加上延时, 实现了 PWM周期, 虽然…...
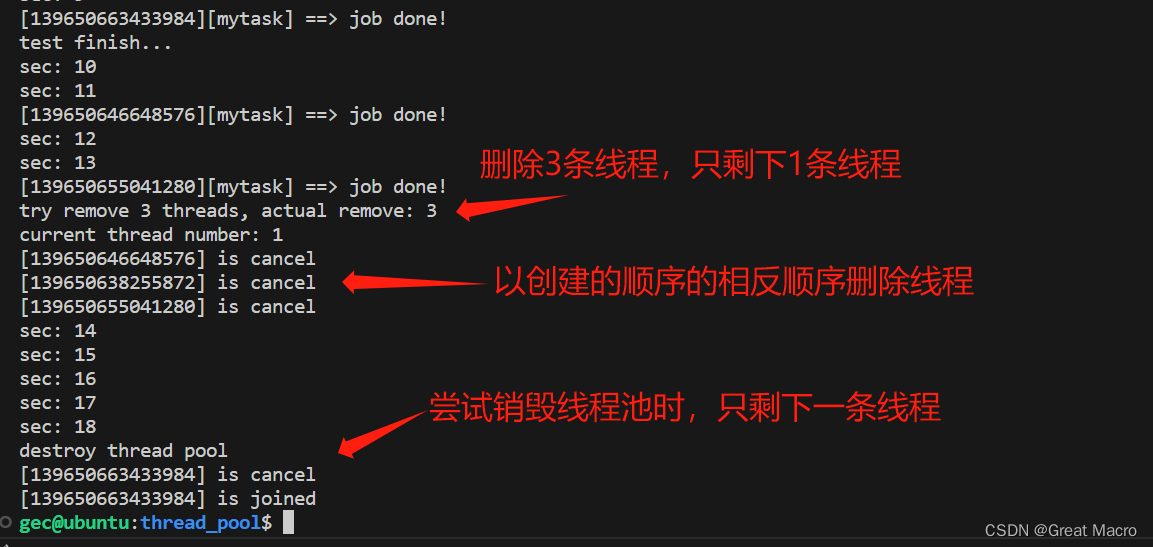
Linux系统编程系列之线程池
Linux系统编程系列(16篇管饱,吃货都投降了!) 1、Linux系统编程系列之进程基础 2、Linux系统编程系列之进程间通信(IPC)-信号 3、Linux系统编程系列之进程间通信(IPC)-管道 4、Linux系统编程系列之进程间通信-IPC对象 5、Linux系统…...

Linux CentOS7 vim多文件与多窗口操作
窗口是可视化的分割区域。Windows中窗口的概念与linux中基本相同。连接xshell就是在Windows中新建一个窗口。而vim打开一个文件默认创建一个窗口。同时,Vim打开一个文件也就会建立一个缓冲区,打开多个文件就会创建多个缓冲区。 本文讨论vim中打开多个文…...

SPI 通信协议
1. SPI通信 1. 什么是SPI通信协议 2. SPI的通信过程 在一开始会先把发送缓冲器的数据(8位)。一次性放到移位寄存器里。 移位寄存器会一位一位发送出去。但是要先放到锁存器里。然后从机来读取。从机的过程也一样。当移位寄存器的数据全部发送完。其实…...
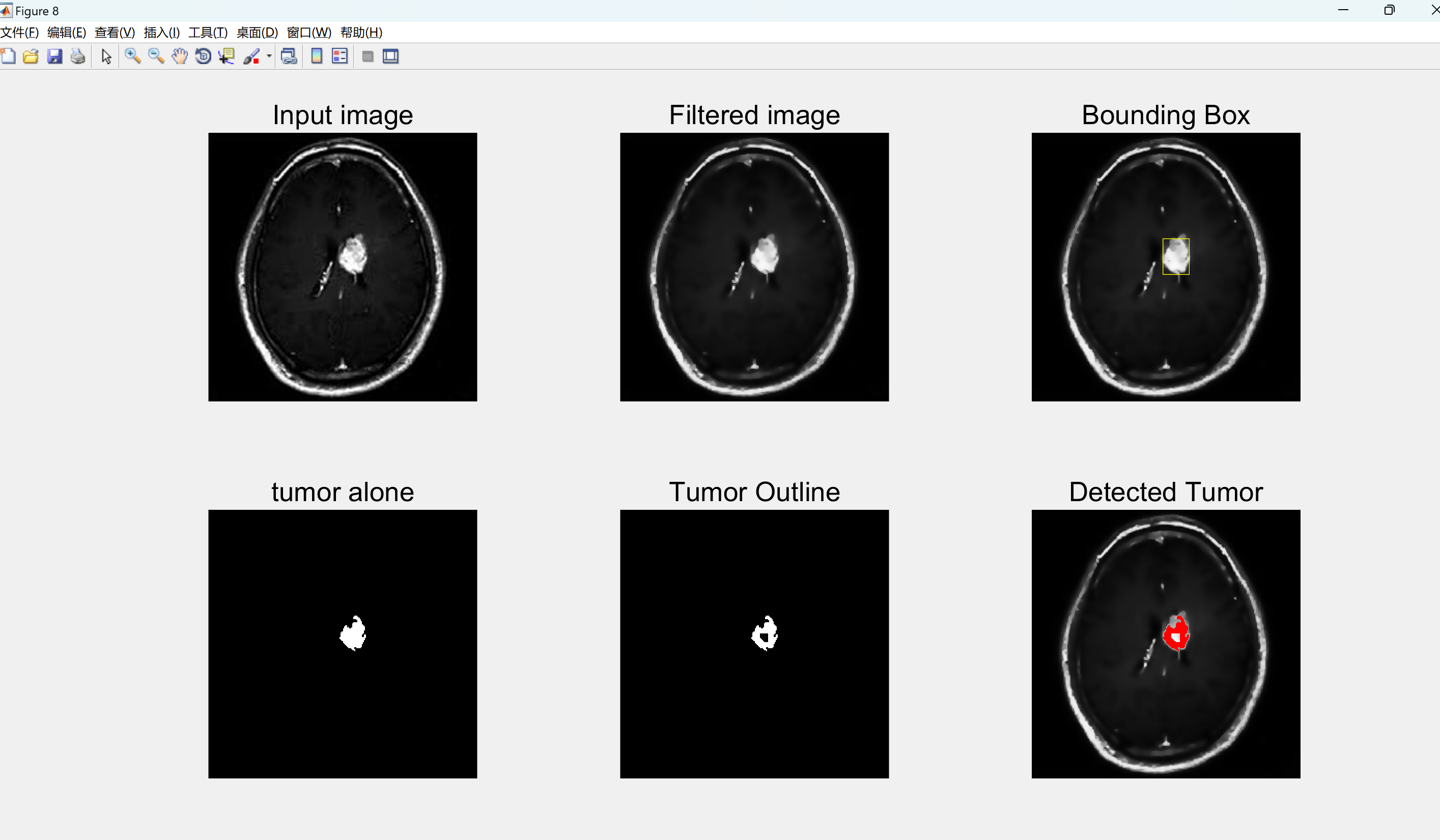
【图像处理】使用各向异性滤波器和分割图像处理从MRI图像检测脑肿瘤(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
5个适合初学者的初级网络安全工作,网络安全就业必看
前言 网络安全涉及保护计算机系统、网络和数据免受未经授权的访问、破坏和盗窃 - 防止数字活动和数据访问的中断 - 同时也保护用户的资产和隐私。鉴于公共事业、医疗保健、金融以及联邦政府等行业的网络犯罪攻击不断升级,对网络专业人员的需求很高,这并…...

Kafka核心原理
1、Topic的分片和副本机制 分片作用: 解决单台节点容量有限的问题,节点多,效率提升,吞吐量提升。通过分片,将一个大的容器分解为多个小的容器,分布在不同的节点上,从而实现分布式存储。 分片…...

探秘前后端开发世界:猫头虎带你穿梭编程的繁忙街区,解锁全栈之路
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

洛谷_分支循环
p2433 问题 5 甲列火车长 260 米,每秒行 12 米;乙列火车长220 米,每秒行 20 米,两车相向而行,从两车车头相遇时开始计时,多长时间后两车车尾相离?已知答案是整数。 计算方式:两车车…...

MySQL数据库入门到精通——进阶篇(3)
黑马程序员 MySQL数据库入门到精通——进阶篇(3) 1. 锁1.1 锁-介绍1.2 锁-全局锁1.3 锁-表级锁1.3.1 表级锁-表锁1.3.2 表级锁元数据锁( meta data lock,MDL)1.3.3 表级锁-意向锁1.3.4 表级锁意向锁测试 1.4 锁-行级锁1.4.1 行级锁-行锁1.4.2…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
