信号的运算与变换
目录
前言
本章内容介绍
信号的运算与变换
相加
相乘
时移
反折
尺度变换
微分(差分)
积分(累加)
信号的奇偶求解
信号的实虚分解
合适的例题
1、时移+反折
2、时移+尺度
3、时移+反折+尺度
4、反求x(t)
前言
《信号与系统》是一门很难的课,也是许多学校考研要考的专业课,由于每周只有两节课,所以每次上完都要及时的去复习,这里参考的教材是奥本海姆著作,刘海棠译,北京:电子工业出版社,2013年。
本章内容介绍
信号与系统分析当中一个重要的概念是关于信号的变化概念。例如,在飞机控制系统中对应于驾驶员动作的信号,经由电和机械的系统变换为飞行推力或飞机控制翼面(如舵或副翼)位置上的改变,进而再进过该机体的动力学和运动学原来变换为飞机速度和航行上的方向上的变化。在这里,我们只关注很有限但很重要的几种最基本的信号变换,且只涉及自变量的简单变换。
信号的运算与变换
在信号的传输及处理过程中往往需要进行信号的运算,包括相加、相乘、移位、反折、尺度变换、以及(微分)差分和积分(累加)等等。
-
相加
两个(或多个)信号之和构成另一个信号,它在任意瞬间的值等于两个或多个信号在同一瞬间的代数和。
连续:x(t)=x1(t)+x2(t)
离散:y[n]=x1[n]+x2[n]
这里就是对应的地方进行相加,只是需要注意离散只有整数有效。
-
相乘
指的是两个(或多个)信号相乘构成另一个信号时,把所有相同瞬间的值一一相乘。
连续:x(t)=x1(t)x2(t)
离散:y[n]=x1[n]x2[n]
与相加有些相同,对应的部分对其进行相乘。
-
时移
遵循一个原则"左加右减",且时移后,形状、幅度不变。
连续信号x(t),设t0>0
x(t-t0),则原信号向右平移t0时间;
x(t-t0),则原信号向左平移t0时间;
离散信号x[n],当m>0
x[n-m]:右移m位
x[n+m]:左移m位
-
反折
即为x(-t),将x(t)沿纵坐标进行反折。
实际就是沿着y轴方向进行对称绘制。
-
尺度变换
将信号x(t)的自变量乘以正系数a为x(at),则:
a>1,将波形进行压缩;
a<1,将波形进行扩展;
压缩和扩展提现在x轴上。
举一个实例:
若x(t)是已录制声音的磁带:
x(-t)表示磁带倒转播放产生的信号
x(2t)表示磁带以二倍速加快播放的结果
x(t/2)表示原磁带放音速度降至一半产生的信号
-
微分(差分)
微分(Differential)
差分(Difference)
一阶前向差分定义为:
一阶后向差分定义为:
-
积分(累加)
积分(Integration)
累加(accumulation)
-
信号的奇偶求解
对于连续信号:
,
则有:
有上面的式子,可以有这样的结论:
对于离散信号也是同样如此。
信号与其偶分量和奇分量之间还满足以下能量关系:
连续信号:
离散信号:
例题:已知下图为x(t),求、
:
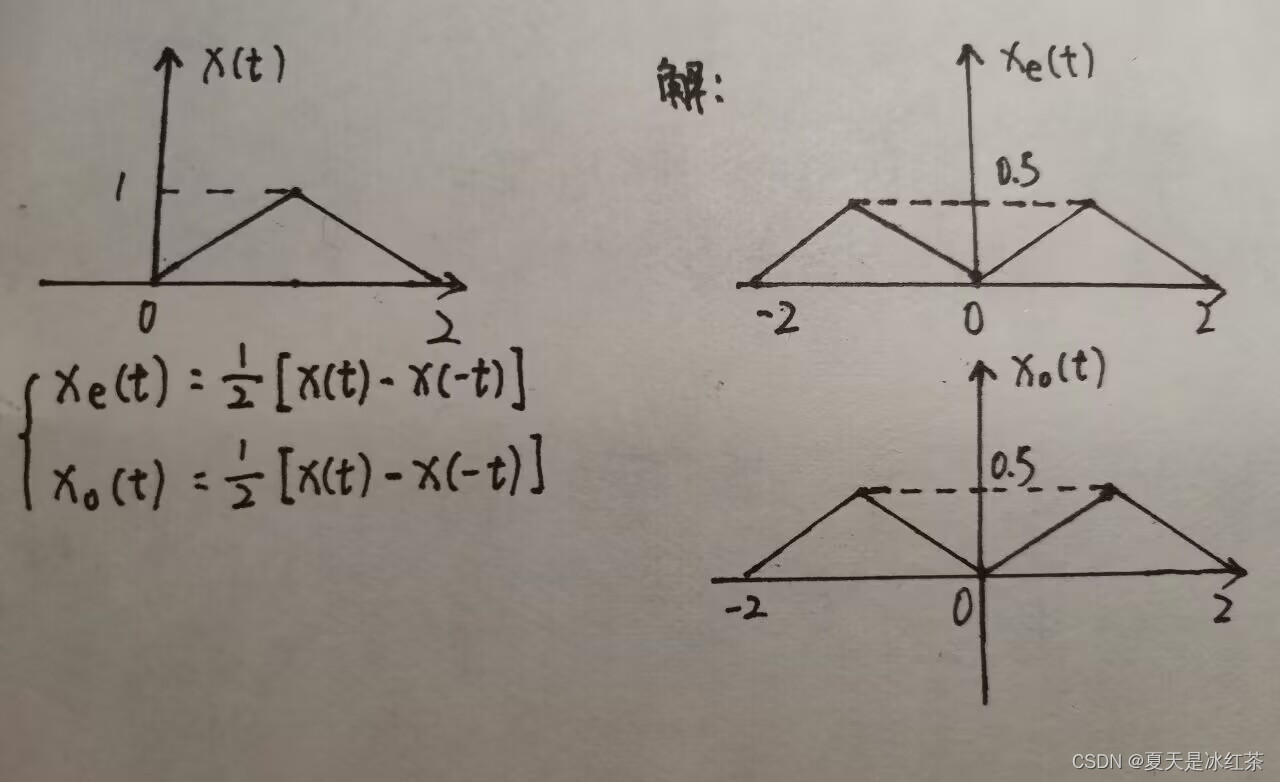
-
信号的实虚分解
则:
合适的例题
既然已经了解了上面的知识,做做这里的例题巩固一下吧。
1、时移+反折
求:x(-t+2)
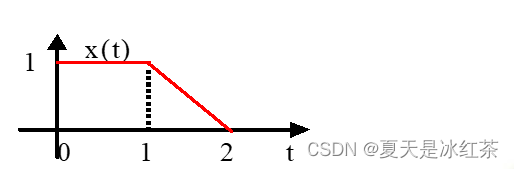

2、时移+尺度
求:x(3t-2)

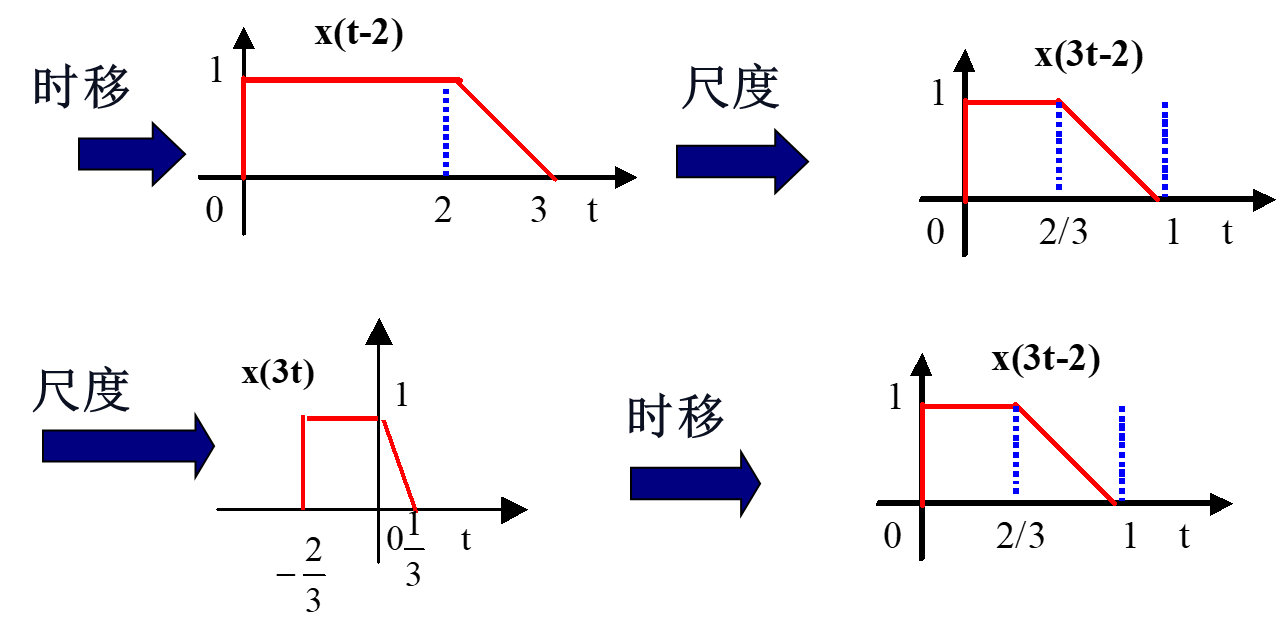
3、时移+反折+尺度
求:x(-3t-2)
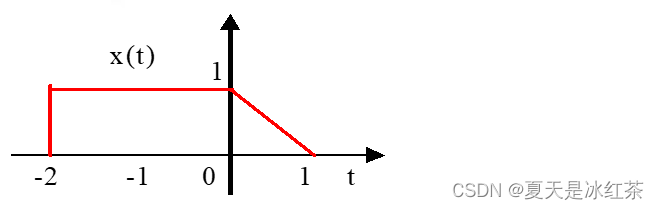
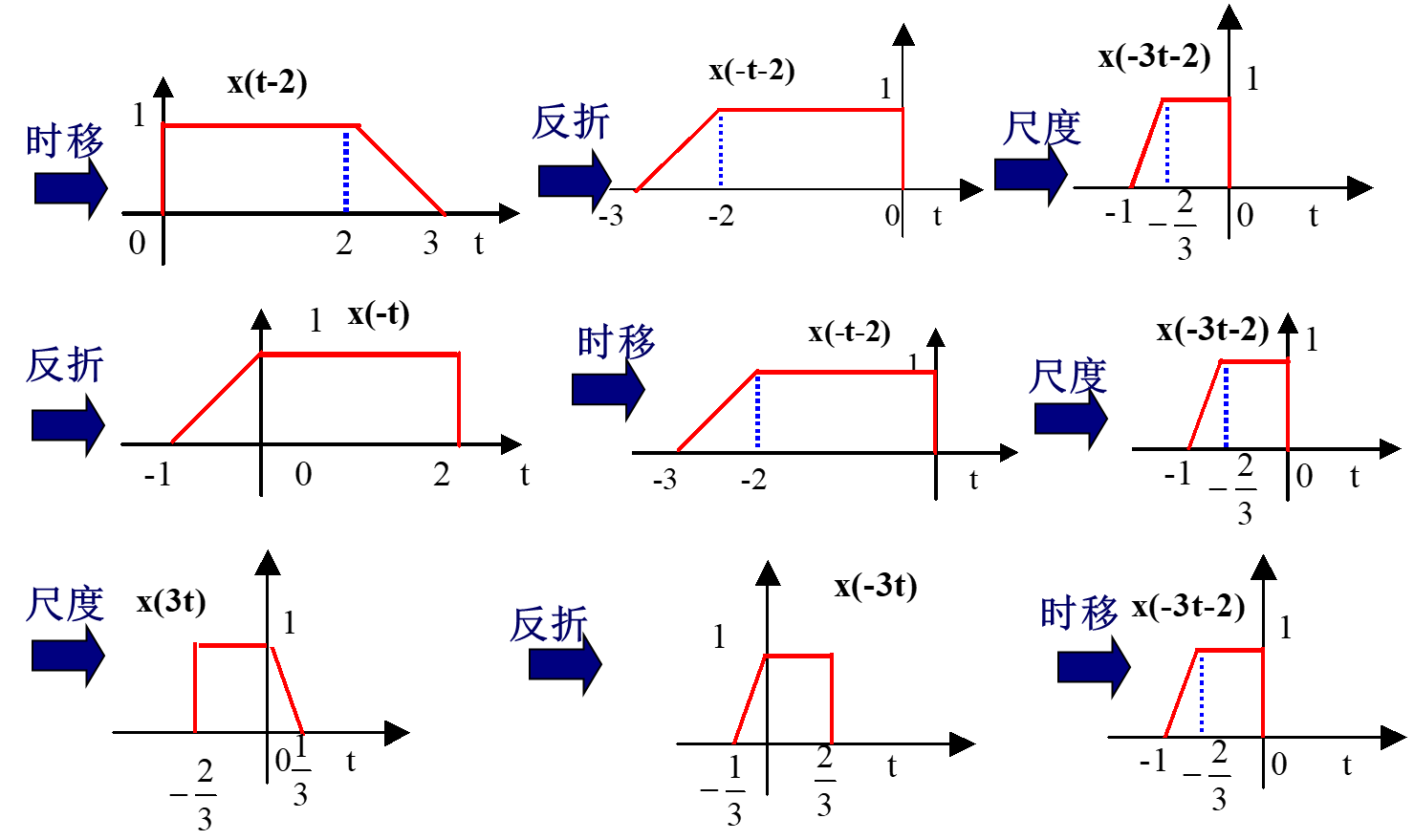
4、反求x(t)
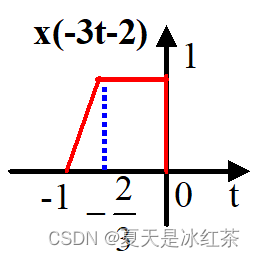
解1:反折-尺度-时移
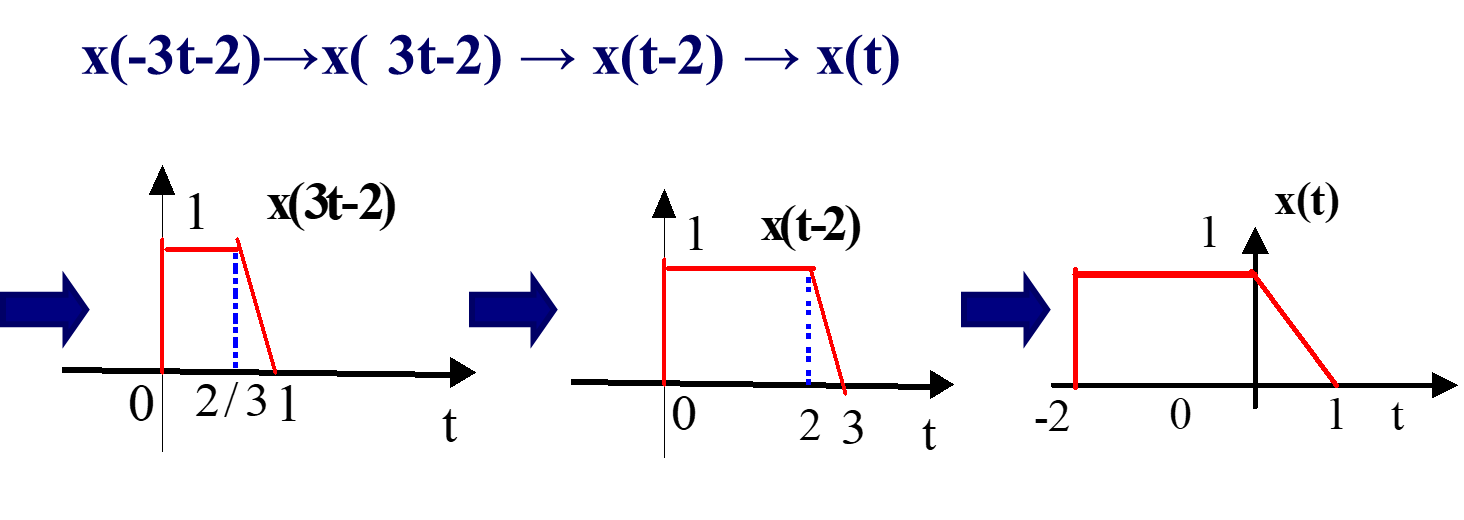
解2:令
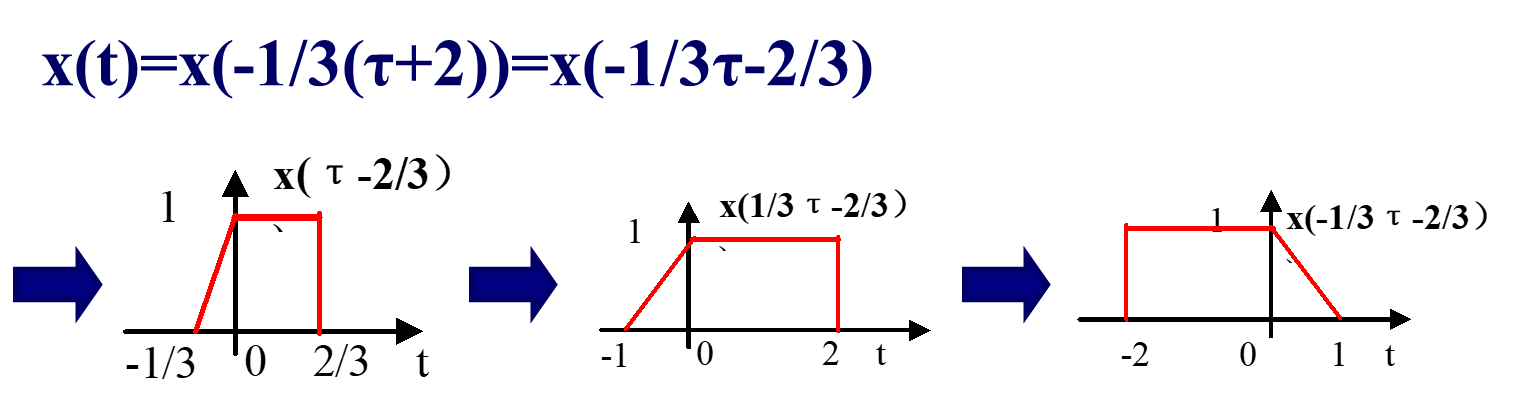
相关文章:
信号的运算与变换
目录 前言 本章内容介绍 信号的运算与变换 相加 相乘 时移 反折 尺度变换 微分(差分) 积分(累加) 信号的奇偶求解 信号的实虚分解 合适的例题 1、时移反折 2、时移尺度 3、时移反折尺度 4、反求x(t) 前言 《信号…...

【GO】K8s 管理系统项目9[API部分--Secret]
K8s 管理系统项目[API部分–Secret] 1. 接口实现 service/dataselector.go // secret type secretCell corev1.Secretfunc (s secretCell) GetCreation() time.Time {return s.CreationTimestamp.Time }func (s secretCell) GetName() string {return s.Name }2. Secret功能…...
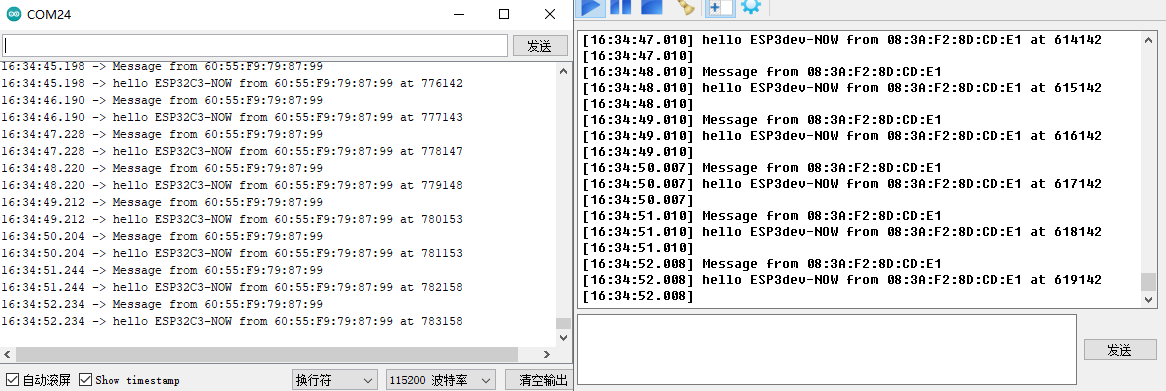
ESP32 Arduino EspNow点对点双向通讯
ESP32 Arduino EspNow点对点双向通讯✨本案例分别采用esp32和esp32C3之间点对点单播无线通讯方式。 🌿esp32开发板 🌾esp32c3开发板 🔧所需库(需要自行导入到Arduino IDE library文件夹中,无法在IDE 管理库界面搜索下载到该库)&am…...
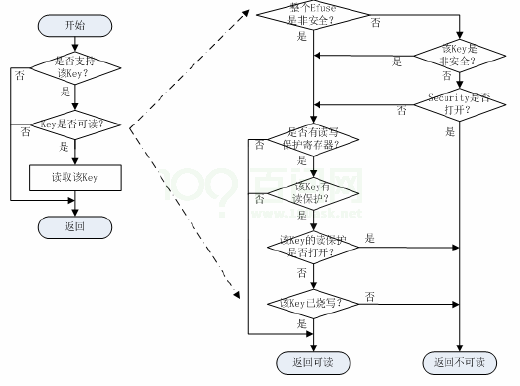
Linux SID 开发指南
Linux SID 开发指南 1 前言 1.1 编写目的 介绍Linux 内核中基于Sunxi 硬件平台的SID 模块驱动的详细设计,为软件编码和维护提供基 础。 1.2 适用范围 内核版本Linux-5.4, Linux-4.9 的平台。 1.3 相关人员 SID 驱动、Efuse 驱动、Sysinfo 驱动的维护、应用开…...
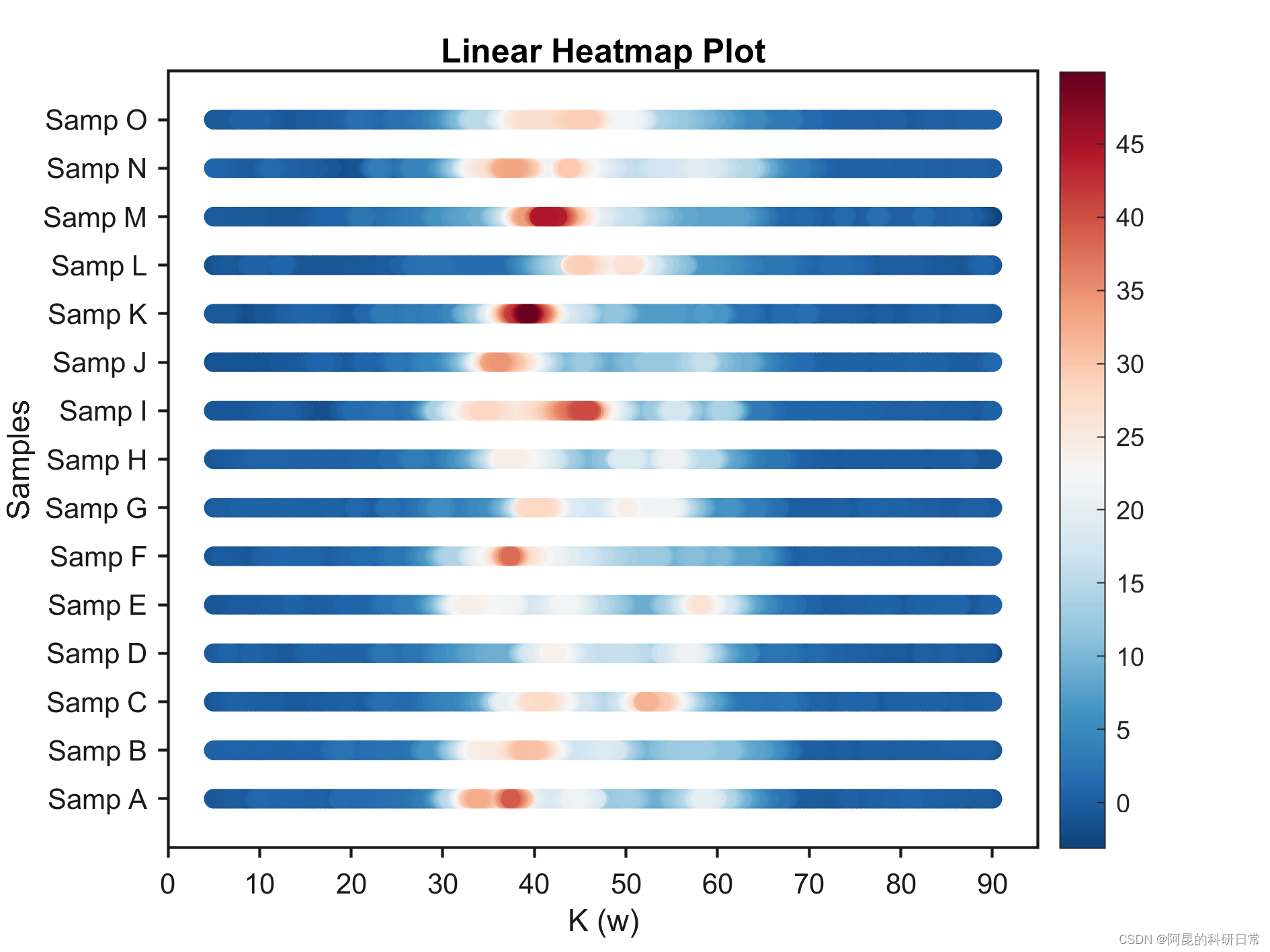
Matlab进阶绘图第2期—线型热图
线型热图由共享X轴的多条渐变直线组成,其颜色表示某一特征值。 与传统热图相比,线型热图适应于X轴数据远多于Y轴(条数)的情况,可以很好地对不同组数据间的分布情况进行比较,也因此可以在一些期刊中看到它的…...

【Redis中bigkey你了解吗?bigkey的危害?】
一.Redis中bigkey你了解吗?bigkey的危害? 如果面试官问到了这个问题,不必惊慌,接下来我们从什么是bigkey?bigkey划分的类型?bigkey危害之处? 二.什么是bigkey?会有什么影响ÿ…...
C++回顾(一)——从C到C++
前言 在学习了C语言的基础上,C到底和C有什么区别呢? 1.1 第一个C程序 #include <iostream>// 使用名为std的命名空间 using namespace std;int main() {// printf ("hello world\n");// cout 标准输出 往屏幕打印内容 相当于C语言的…...

CRF条件随机场 | 关键原理+面试知识点
😄 CRF之前跟人生导师:李航学习过,这里结合自己的理解,精简一波CRF,总结一下面试中高频出现的要点。个人觉得没网上说的那么复杂,我看网上很大部分都是一长篇先举个例子,然后再说原理。没必要原理其实不难,直接从原理下手更好理解。 文章目录 1、概率无向图(马尔可夫…...
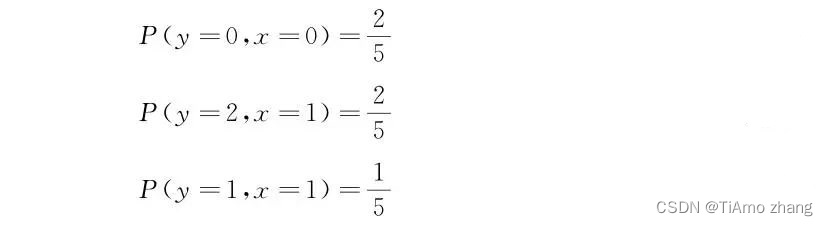
秒懂算法 | 回归算法中的贝叶斯
在本文中,我们会用概率的观点来看待机器学习模型,用简单的例子帮助大家理解判别式模型和生成式模型的区别。通过思考曲线拟合的问题,发现习以为常的损失函数和正则化项背后有着深刻的意义 01、快速理解判别式模型和生成式模型 从概率的角度来理解数据有着两个不同的角度,假…...

用Netty实现物联网01:XML-RPC和JSON-RPC
最近十年,物联网和云计算、人工智能等技术一道,受到业内各方追捧,被炒得火热,甚至还诞生了AIoT这样的技术概念。和(移动)互联网不同,物联网针对的主要是一些资源有限的硬件设备,比如监控探头、烟雾感应器、温湿度感应器、车载OBD诊断器、智能电表、智能血压计等。这些硬…...

腾讯云服务器centos7安装python3.7+,解决ssl问题
使用requests模块访问百度,报错如下: requests.exceptions.SSLError: HTTPSConnectionPool(hostwww.baidu.com, port443): Max retries exceeded with url: / (Caused by SSLError("Cant connect to HTTPS URL because the SSL module is not avail…...

C++【模板STL简介】
文章目录C模板&&STL初阶一、泛型编程二、函数模板2.1.函数模板概念2.2.函数模板格式2.3.函数模板的实例化2.4.模板参数的匹配原则三、 类模板3.1.模板的定义格式3.2.类模板的实例化STL简介一、STL的概念、组成及缺陷二、STL的版本C模板&&STL初阶 一、泛型编程…...

该学会是自己找bug了(vs调试技巧)
前言 🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨ 🐻推荐专栏: 🍔🍟🌯 c语言初阶 🔑个人信条: 🌵知行合一 🍉本篇简介:>:介绍c语言初阶的最后一篇.有关调试的重要性. 金句分享…...
)
Redis大全(概念与下载安装)
目录 一、概念 1.非关系型数据库(NoSQL)的介绍 2.什么是redis 3.redis的作者 4.Redis的特点 5.redis的应用场景 6.高度概括知识 一、二 缓存穿透、缓存击穿、缓存雪崩的概念 (一)缓存穿透 (二)缓…...

指针的进阶【上篇】
文章目录📀1.字符指针📀2.指针数组📀3.数组指针💿3.1.数组指针的定义💿3.2. &数组名VS数组名💿3.3.数组指针的使用📀1.字符指针 int main() {char ch w;char* pc &ch;// pc就是字符指…...

MATLAB | 如何用MATLAB绘制花里胡哨的山脊图
本期推送教大家如何绘制各种样式的山脊图,这里做了一个工具函数用来实现好看的山脊图的绘制,编写不易请多多点赞,大体绘制效果如下: 依旧工具函数放在文末。 教程部分 0 数据准备 数据为多个一维向量放在元胞数组中,…...
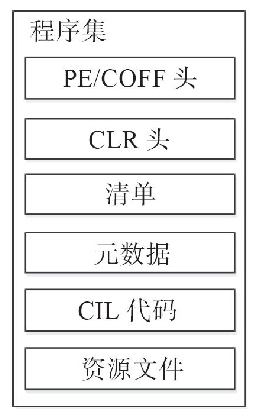
.Net与程序集
一个简单的C#程序回想一下我们第一个.net 程序 hello world,它具有那些步骤呢?打开visual studio创建一个C# console的项目build运行程序这时候就有一个命令行窗口弹出来,上面打印着hello world。我们打开文件夹的bin目录,会发现里…...

软考中级之数据库系统(重点)
涉及考点:数据库模式,ER模型,关系代数与元祖演算,规范化理论,并发控制,分布式数据库系统,数据仓库和数据挖掘 数据库模式 三级模式-二级映射 常考选择题 三级模式,两种映射的这种涉及属于层次架构体的设计,这种设计为我们在应用数据库的时候提供了很多便利,同时提高了整个体…...
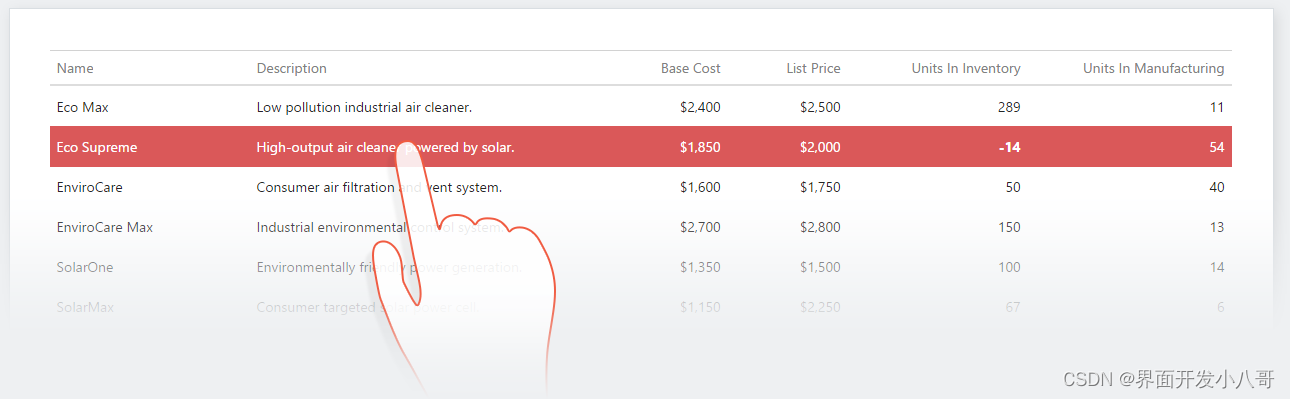
界面控件DevExtreme的Data Grid组件——让业务信息管理更轻松!
DevExtreme拥有高性能的HTML5 / JavaScript小部件集合,使您可以利用现代Web开发堆栈(包括React,Angular,ASP.NET Core,jQuery,Knockout等)构建交互式的Web应用程序,该套件附带功能齐…...
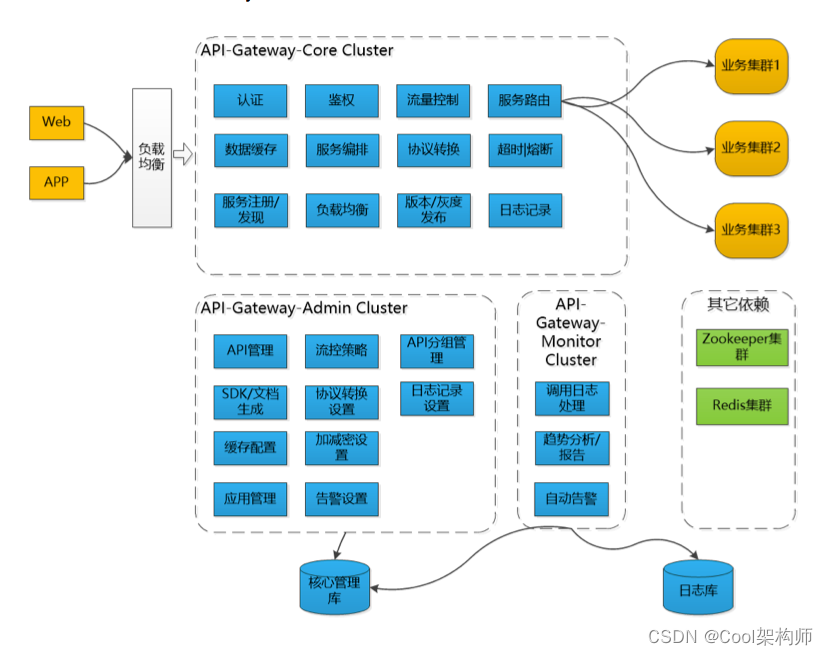
【架构师】零基础到精通——网关策略
博客昵称:架构师Cool 最喜欢的座右铭:一以贯之的努力,不得懈怠的人生。 作者简介:一名退役Coder,软件设计师/鸿蒙高级工程师认证,在备战高级架构师/系统分析师,欢迎关注小弟! 博主小…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
