二叉树的顺序存储——堆——初识堆排序
前面我们学过可以把完全二叉树存入到顺序表中,然后利用完全二叉树的情缘关系,就可以通过数组下标来联系。
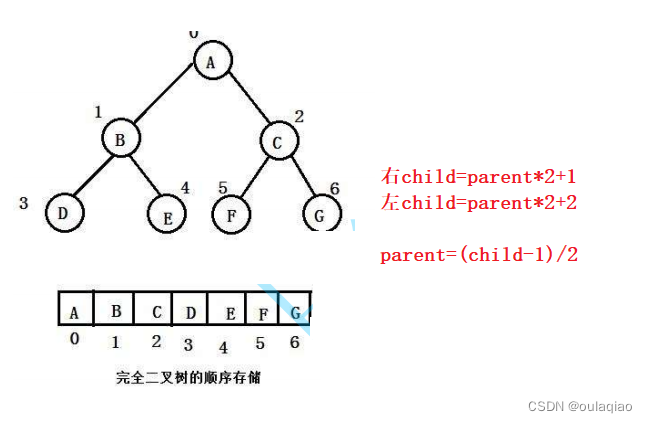
但是并不是把二叉树存入到数组中就是堆了,要看原原来的二叉树是否满足:所有的父都小于等于子,或者所有的父都大于等于子——既小堆大堆
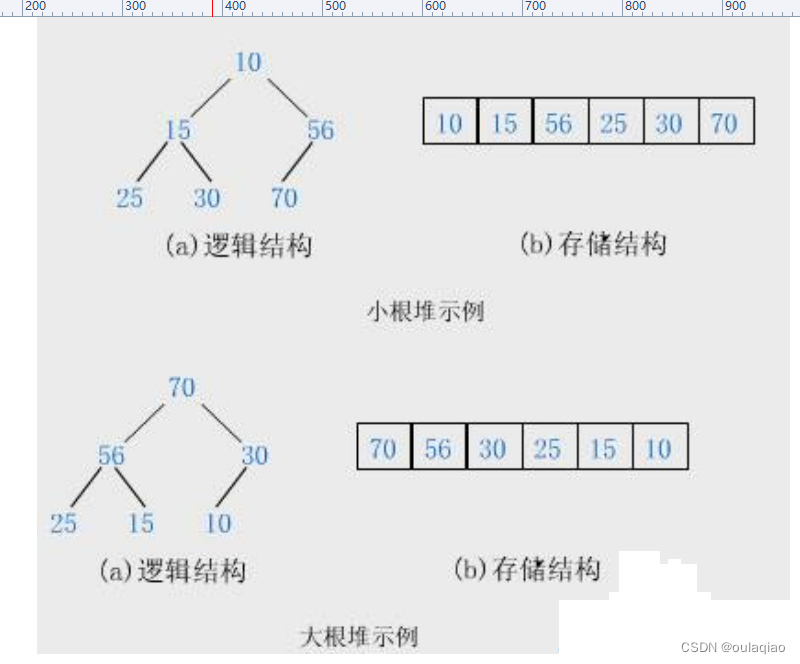
现在我们用代码来实现数据存入到顺序表中,并且是小堆
首先需要创建一个顺序表的结构体

然后初始化
void HeapInit(Heap* php)//初始化
{assert(php);php->a = NULL;php->capacity = php->size = 0;
}
放入数据
首先要用指针开辟一块空间并判断是否需要扩容,然后把数据尾插进去
void HeapPush(Heap* php, HpDatatype x)//放入数据
{assert(php);//扩容if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HpDatatype* tmp = (HpDatatype*)realloc(php->a, sizeof(HpDatatype)*newcapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;Adjust(php->a, php->size - 1);//调整
}
但是因为这个数组要满足小堆,所以尾插进去的数还需要进一步的调整
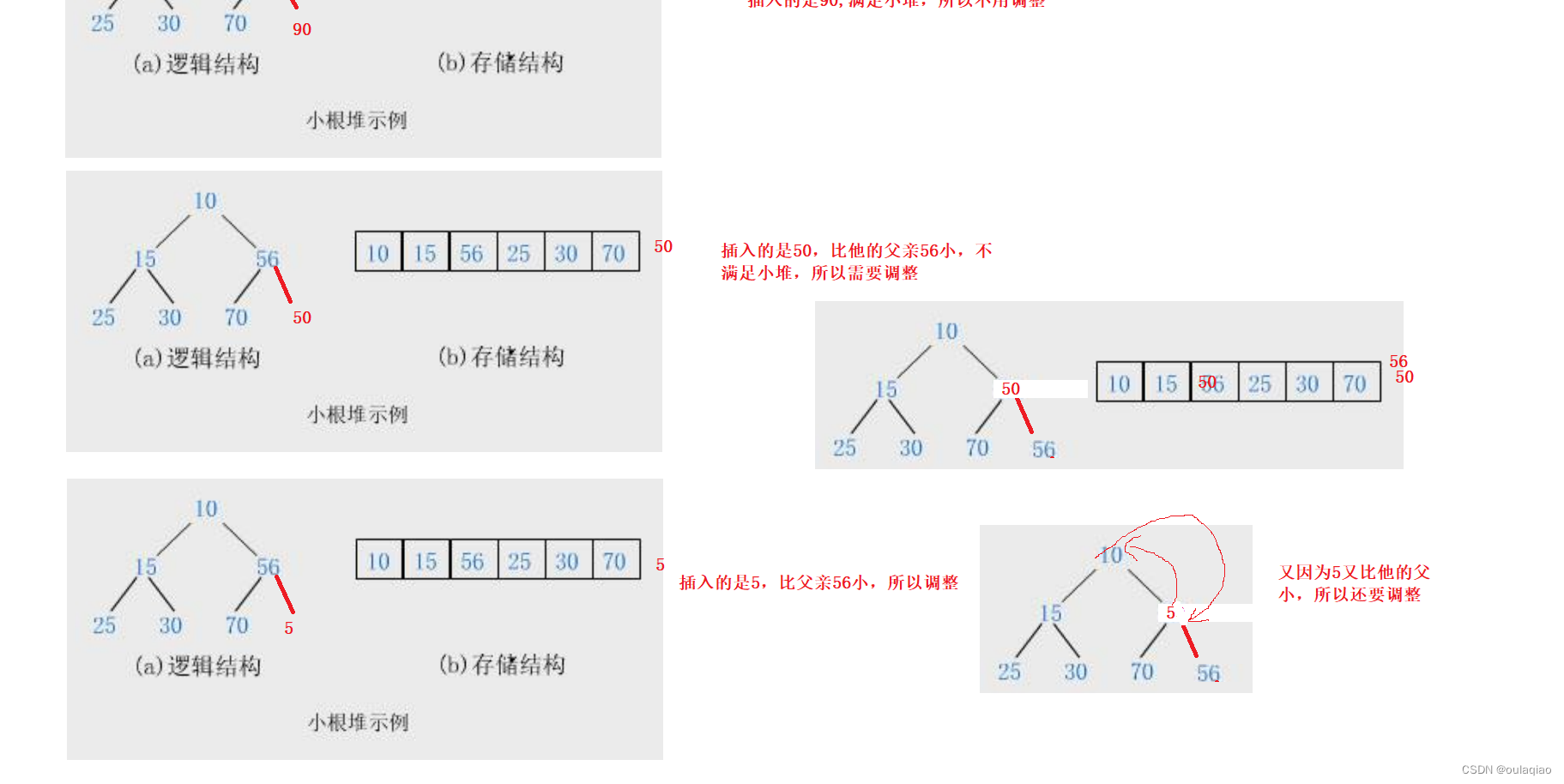
那么这里的代码是如何实现的呢
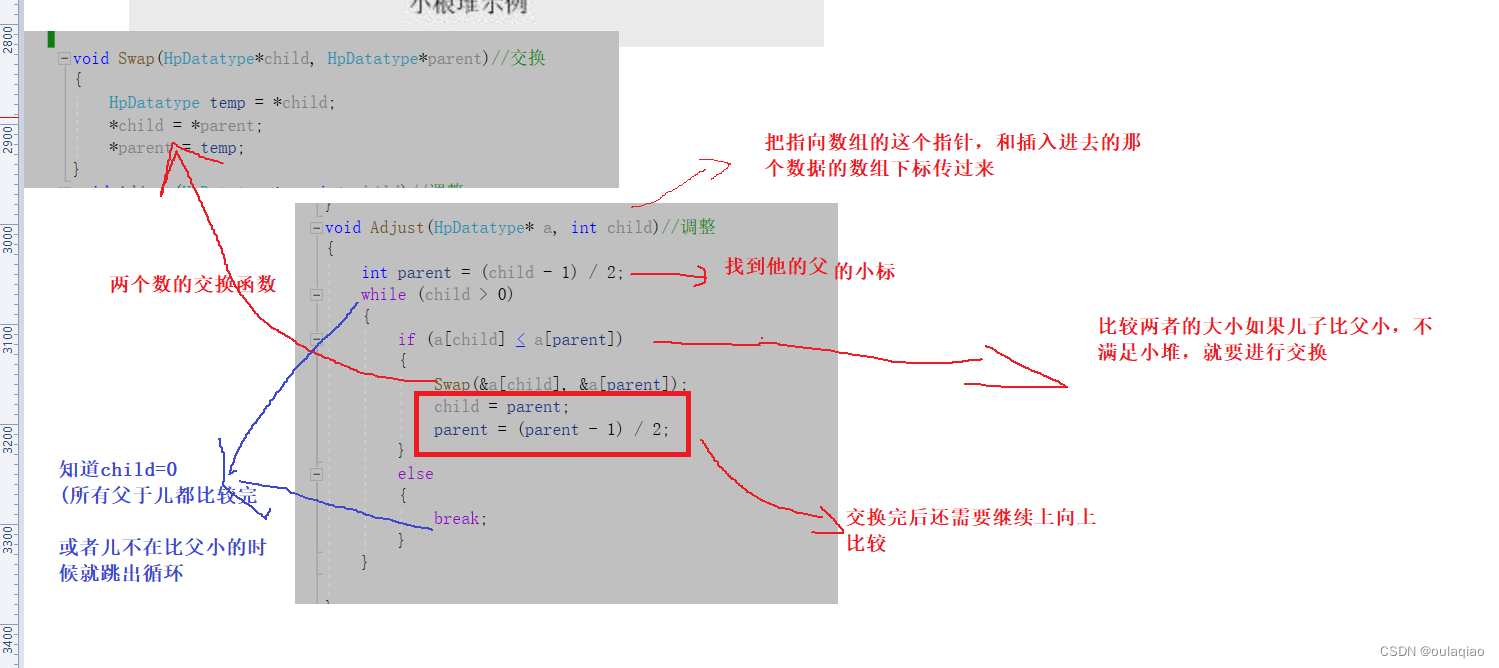
到这里的时候我们没插入一个数据就都可以把数据从新调整为一个堆,那么我们为什么要把数据按照堆的方式存储呢?
现在我们来写一个堆数据删除的代码就能感受到堆的作用:
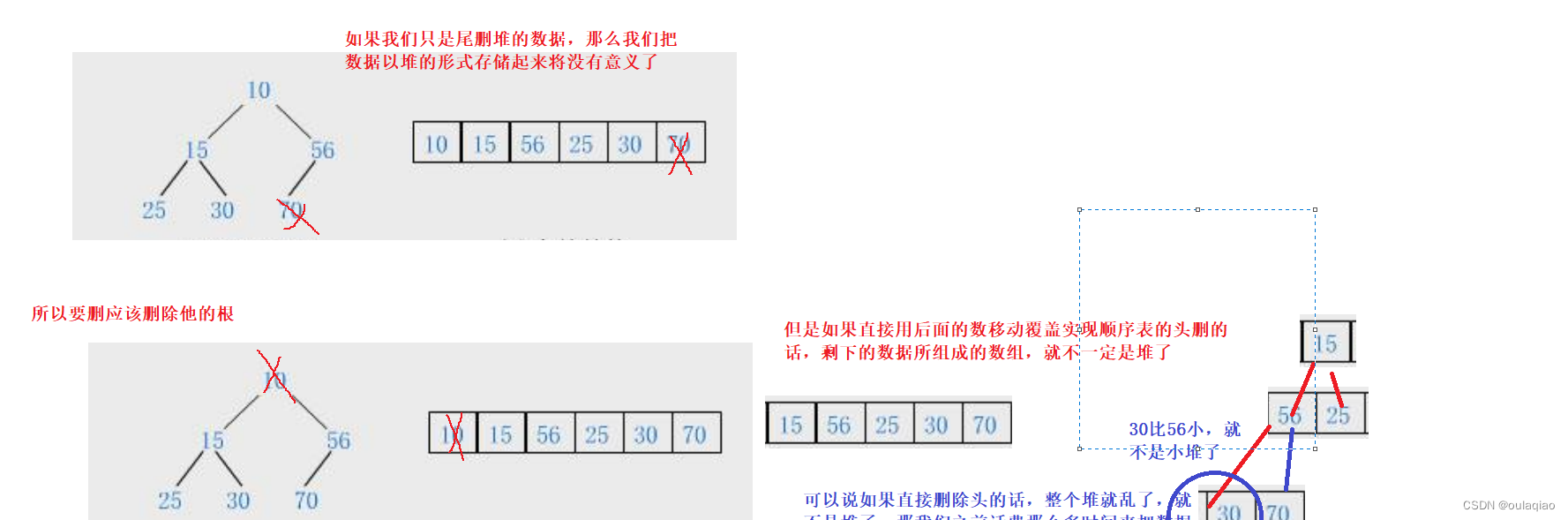
void AdiustDown(HpDatatype* a, int n, int parent)
{int child = parent * 2 + 1;//先假设和根交换的是他的左儿子while (child<n)//当child=parent*2+1已经超出了数组的范围,那么就说明他下面已经没有儿子了,此时也是结束循环{if (child+1<n && a[child + 1] < a[child])//如果假设错误,那么就换成右儿子,但是这里要注意的child+1(右儿子)存在{child++;}if (a[child] < a[parent])//判断是否需要换{Swap(&a[child], &a[parent]);//交换//尾下一次循环做准备parent = child;child = parent * 2 + 1;}else//如果不用换就直接跳出循环{break;}}
}void HeapPop(Heap* php)//删除根
{assert(php);assert(php->size>0);Swap(&php->a[0], &php->a[php->size - 1]);//交换php->size--;//尾删//向下调整AdiustDown(php->a, php->size, 0);}有了这个删根代码,我们在加上取根代码,和判空代码,便可实现数据的排序打印
HpDatatype HeapTop(Heap* php)//返回根值
{assert(php);assert(php->size > 0);return php->a[0];
}bool HeapEmpty(Heap* php)//判空
{assert(php);return php->size==0;
}
while (!HeapEmpty(&st)){printf("%d ", HeapTop(&st));//打印顶值HeapPop(&st);}
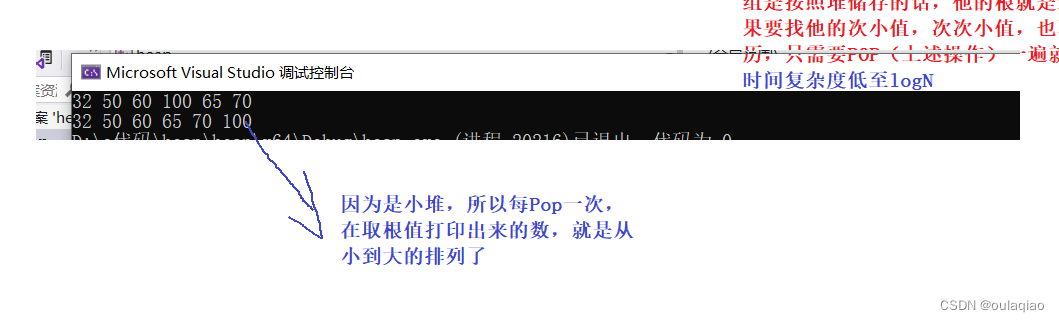
如果把上面插入数据和删除根向下调整的判断语句的小于改成大于那么就实现了打印出来的数据时从大到小的排序
这里就体现出了堆的魅力,当一组数据时以堆的形式储存的,那么他在排序的时候的时间复杂度就是
O(logN2),而之前我们学习的冒泡排序的时间复杂度是O(N2),显然堆的排序时间复杂度更低
但是这里平不是用堆来排序的实际用法,因为如果给我们一个数组,进行排序,我们是要实际改变数组里面值的位置,并不是像这里这样pop一次然后取根打印出来,即使我们每次用取出来的根值去覆盖原来的数组,那么我们要用这样的堆就需要写上面所以的建立堆的数据结构代码,显然是太麻烦了。
那么我们是否可以:
把给的数组变成堆的时候我们就要进行排序,因为这里并没有上面写的数据结构的堆,所以我们无法取根然后再打印,——之前也说了这种方法是不会把原本的数组改变成有有序的,
所以之下要讲的才是如何在把一个数组已经变成堆的情况下进行排序:
降序排序-——恰恰是把数组变成大堆,升序排序恰恰是把数组变成小堆
为什么要这样呢?

升序代码:
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>void Swap(int* child, int* parent)//交换
{int temp = *child;*child = *parent;*parent = temp;
}Adjust(int* a, int child)//向上调整形成堆
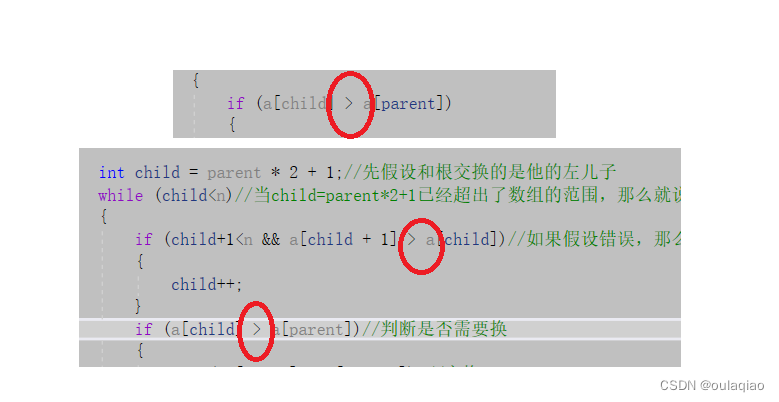
{int parent = (child - 1) / 2;while (child > 0){if (a[parent] < a[child]){Swap(&a[parent], &a[child]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}AdiustDown(int* a, int n, int parent)//向下调整
{int child = parent * 2 + 1;while (child<n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child],&a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
int main()
{
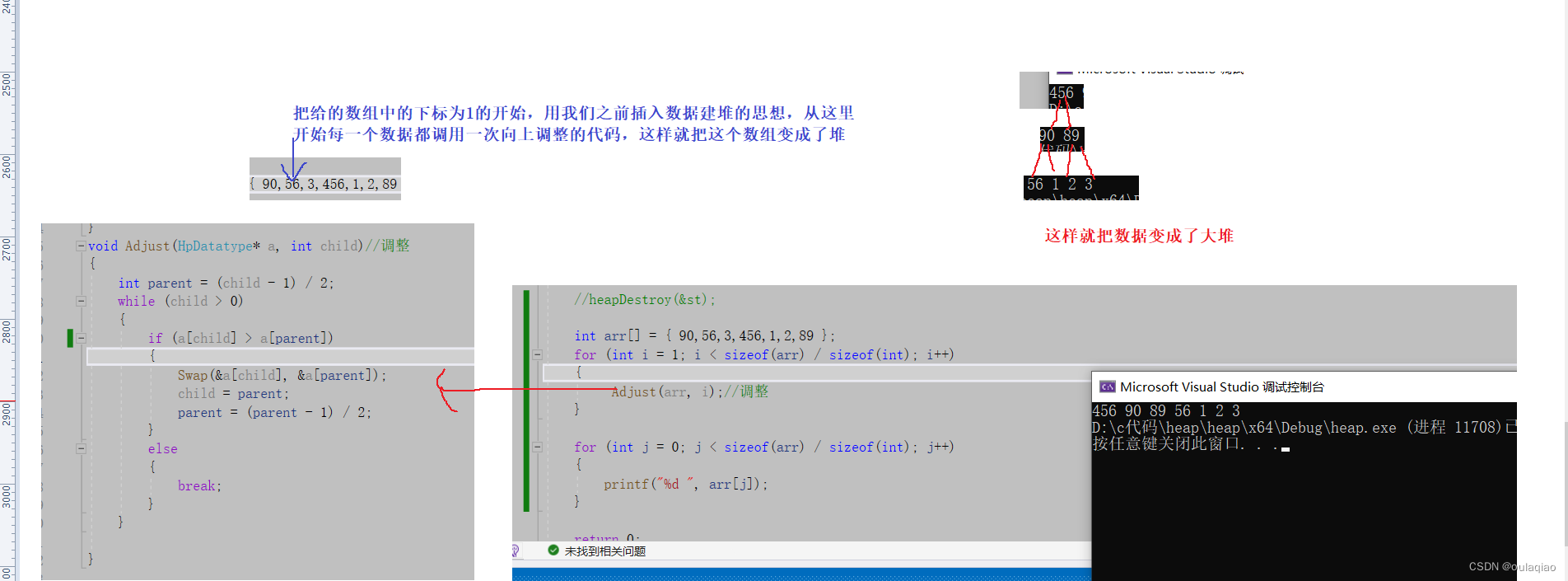
int arr[] = { 90,56,3,46,1,2,89 };
int n = sizeof(arr) / sizeof(int);
for (int i = 1; i < n; i++)
{Adjust(arr, i);//调整
}
int end = n - 1;//最后一个数的下标
while (end > 0)
{Swap(&arr[0], &arr[end]);//向下调整AdiustDown(arr, end, 0);end--;
}for (int j = 0; j < n; j++)
{printf("%d ", arr[j]);
}return 0;
}
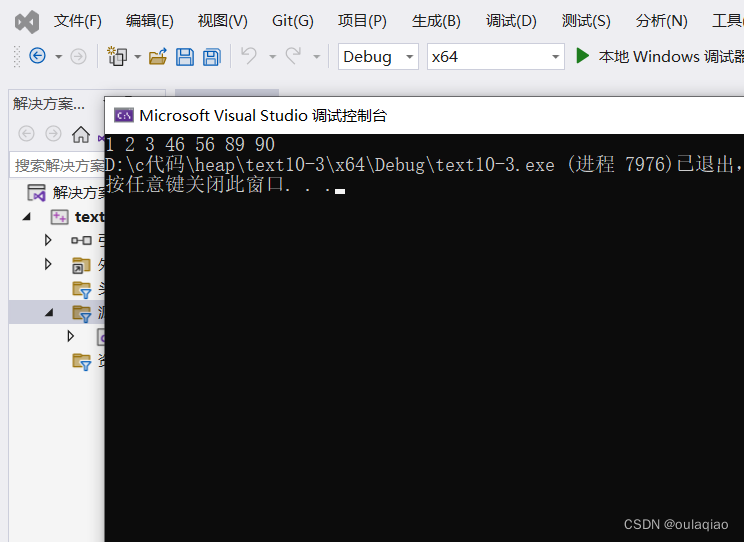
相关文章:

二叉树的顺序存储——堆——初识堆排序
前面我们学过可以把完全二叉树存入到顺序表中,然后利用完全二叉树的情缘关系,就可以通过数组下标来联系。 但是并不是把二叉树存入到数组中就是堆了,要看原原来的二叉树是否满足:所有的父都小于等于子,或者所有的父都…...

CYEZ 模拟赛 9
A a ⊥ b ⇒ a − b ⊥ a b (1) a \perp b \Rightarrow a-b \perp ab \tag {1} a⊥b⇒a−b⊥ab(1) 证明: gcd ( a , b ) gcd ( b , a − b ) \gcd(a,b) \gcd(b, a-b) gcd(a,b)gcd(b,a−b),故 a − b ⊥ b a - b \perp b a−b⊥b,同…...
typescript: Builder Pattern
/*** file: CarBuilderts.ts* TypeScript 实体类 Model* Builder Pattern* 生成器是一种创建型设计模式, 使你能够分步骤创建复杂对象。* https://stackoverflow.com/questions/12827266/get-and-set-in-typescript* https://github.com/Microsoft/TypeScript/wiki/…...
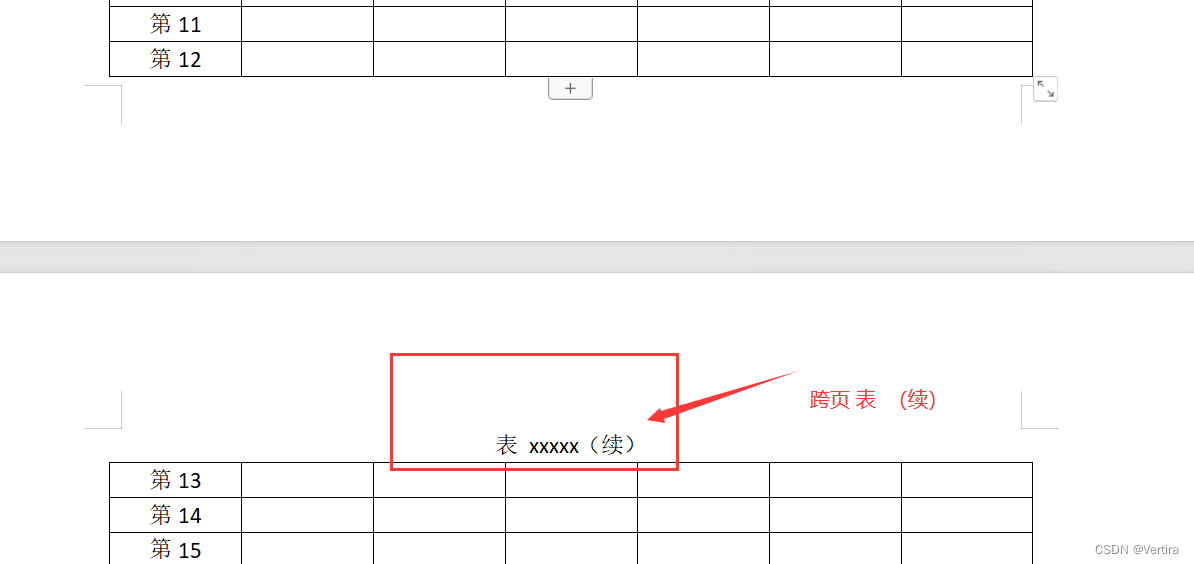
WPS/word 表格跨行如何续表、和表的名称
1:具体操作: 将光标定位在跨页部分的第一行任意位置,按下快捷键ctrlshiftenter,就可以在跨页的表格上方插入空行(在空行可以写,表1-3 xxxx(续)) 在空行中输入…...
Python的NumPy库(一)基础用法
NumPy库并不是Python的标准库,但其在机器学习、大数据等很多领域有非常广泛的应用,NumPy本身就有比较多的内容,全部的学习可能涉及许多的内容,但我们在这里仅学习常见的使用,这些内容对于我们日常使用NumPy是足够的。 …...
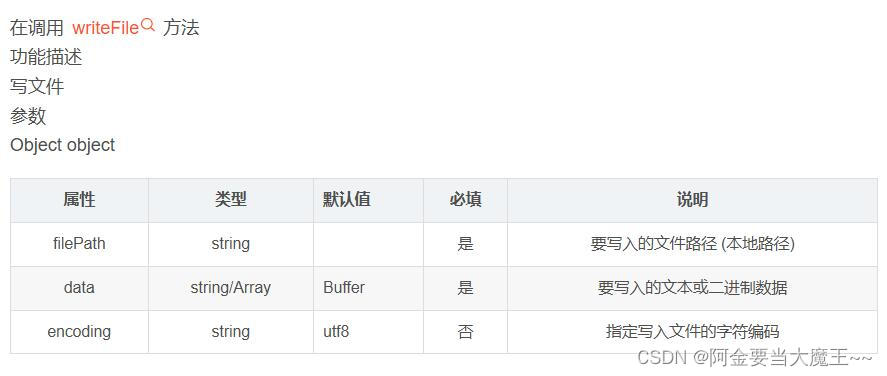
uniapp app 导出excel 表格
直接复制运行 <template><view><button click"tableToExcel">导出一个表来看</button><view>{{ successTip }}</view></view> </template><script>export default {data() {return {successTip: }},metho…...
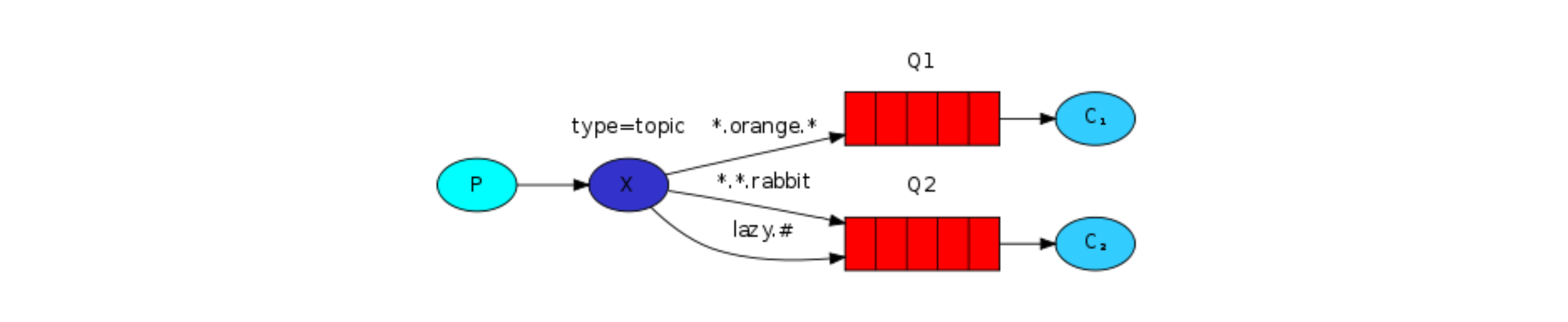
【RabbitMQ】常用消息模型详解
文章目录 AMQP协议的回顾RabbitMQ支持的消息模型第一种模型(直连)开发生产者开发消费者生产者、消费者开发优化API参数细节 第二种模型(work quene)开发生产者开发消费者消息自动确认机制 第三种模型(fanout)开发生产者开发消费者 第四种模型(Routing)开发生产者开发消费者 第五…...

图像拼接后丢失数据,转tiff报错rasterfile failed: an unknown
图像拼接后丢失数据 不仅是数据丢失了,还有个未知原因报错 部分数据存在值不存在的情况 原因 处理遥感数据很容易,磁盘爆满了 解决方案 清理一些无用数据,准备买个2T的外接硬盘用着了。 然后重新做处理...

Nginx之日志模块解读
目录 基本介绍 配置指令 access_log(访问日志) error_log( 错误日志) 基本介绍 Nginx日志主要分为两种:access_log(访问日志)和error_log(错误日志)。Nginx日志主要记录以下信息: 记录Nginx服务启动…...
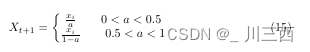
latex方程组编写,一种可以保证方程编号自适应的方法
问题描述: 在利用latex编写方程组时,可以有很多种方法,但不总是编辑好的公式能够显示出编号,故提出一种有效的方程组编写方法 方法: \begin{equation}X_{ t1}\left \{ \begin{matrix}\frac{x_{i}}{a} \quad\quad 0&l…...
深度学习基础 2D卷积(1)
什么是2D卷积 2D参数量怎么计算 以pytorch为例子,2D卷积在设置的时候具有以下参数,具有输入通道的多少(这个决定了卷积核的通道数量),滤波器数量,这个是有多少个滤波器,越多提取的特征就越有用…...

OpenCV DNN C++ 使用 YOLO 模型推理
OpenCV DNN C 使用 YOLO 模型推理 引言 YOLO(You Only Look Once)是一种流行的目标检测算法,因其速度快和准确度高而被广泛应用。OpenCV 的 DNN(Deep Neural Networks)模块为我们提供了一个简单易用的 API࿰…...
第八章 Linux文件系统权限
目录 8.1 文件的一般权限 1.修改文件或目录的权限---chmod命令 2.对于文件和目录,r,w,x有不同的作用: 3.修改文件或目录的所属主和组---chown,chgrp 8.2 文件和目录的特殊权限 三种通过字符描述文件权限 8.3 ACL 权限 1.A…...
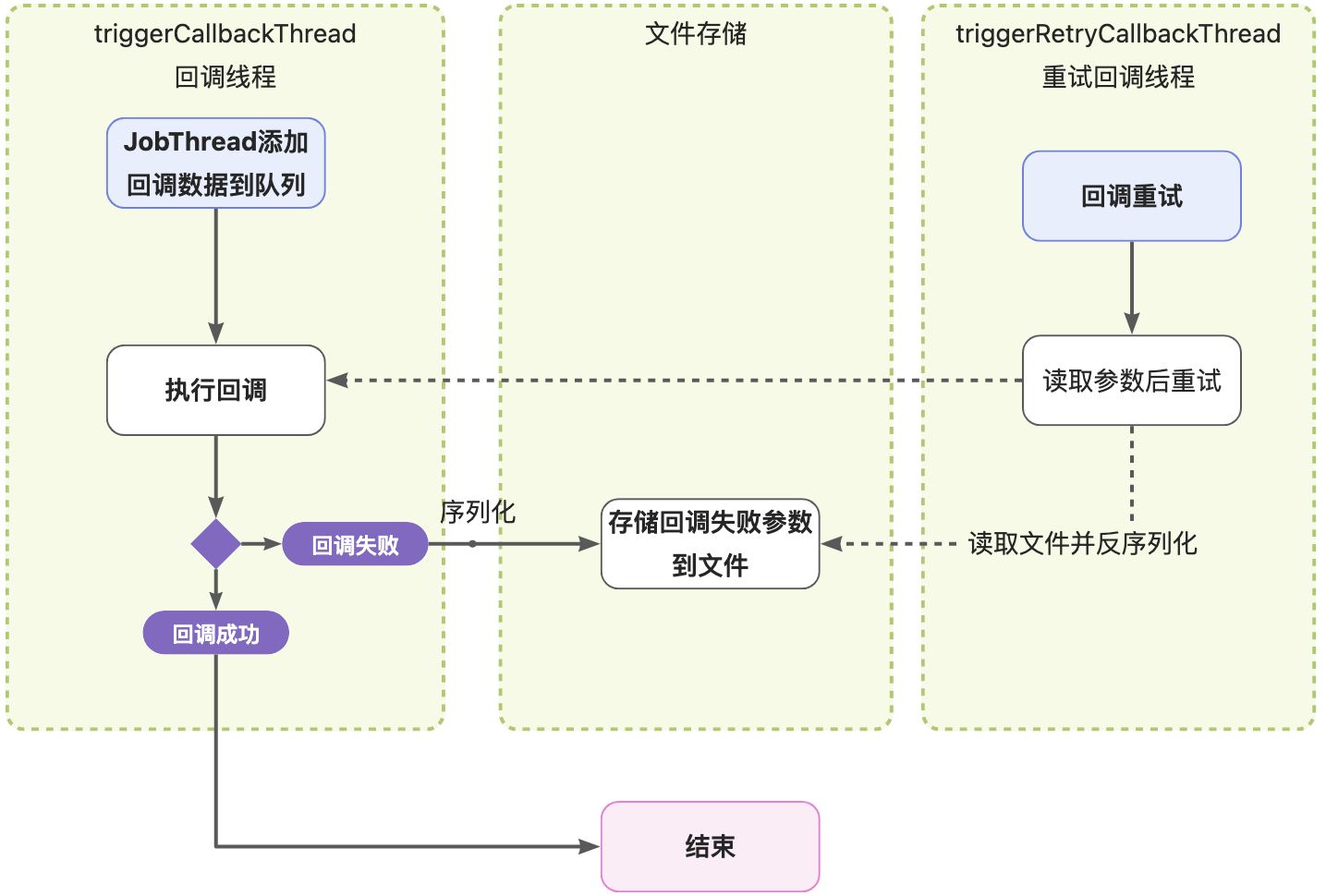
XXL-JOB源码梳理——一文理清XXL-JOB实现方案
分布式定时任务调度系统 流程分析 一个分布式定时任务,需要具备有以下几点功能: 核心功能:定时调度、任务管理、可观测日志高可用:集群、分片、失败处理高性能:分布式锁扩展功能:可视化运维、多语言、任…...
java做个qq机器人
前置的条件 机器人是基于mirai框架实现的。根据官方的文档,建议使用openjdk11。 我这里使用的编辑工具是idea2023 在idea中新建一个maven项目,虽然可以使用gradle进行构建,不过我这里由于网络问题没有跑通。 pom.xml <dependency>&l…...

前端 | AjaxAxios模块
文章目录 1. Ajax1.1 Ajax介绍1.2 Ajax作用1.3 同步异步1.4 原生Ajax 2. Axios2.1 Axios下载2.2 Axios基本使用2.3 Axios方法 1. Ajax 1.1 Ajax介绍 Ajax: 全称(Asynchronous JavaScript And XML),异步的JavaScript和XML。 1.2 Ajax作用 …...

高效的ProtoBuf
一、背景 Google ProtoBuf介绍 这篇文章我们讲了怎么使用ProtoBuf进行序列化,但ProtoBuf怎么做到最高效的,它的数据又是如何压缩的,下面先看一个例子,然后再讲ProtoBuf压缩机制。 二、案例 网上有各种序列化方式性能对比&#…...

删除SQL记录
删除记录的方式汇总: 根据条件删除:DELETE FROM tb_name [WHERE options] [ [ ORDER BY fields ] LIMIT n ] 全部删除(表清空,包含自增计数器重置):TRUNCATE tb_namedelete和truncate的区别: d…...

数据结构--》探索数据结构中的字符串结构与算法
本文将带你深入了解串的基本概念、表示方法以及串操作的常见算法。通过深入理解串的相关概念和操作,我们将能够更好地应用它们来解决算法问题。 无论你是初学者还是进阶者,本文将为你提供简单易懂、实用可行的知识点,帮助你更好地掌握串在数据…...
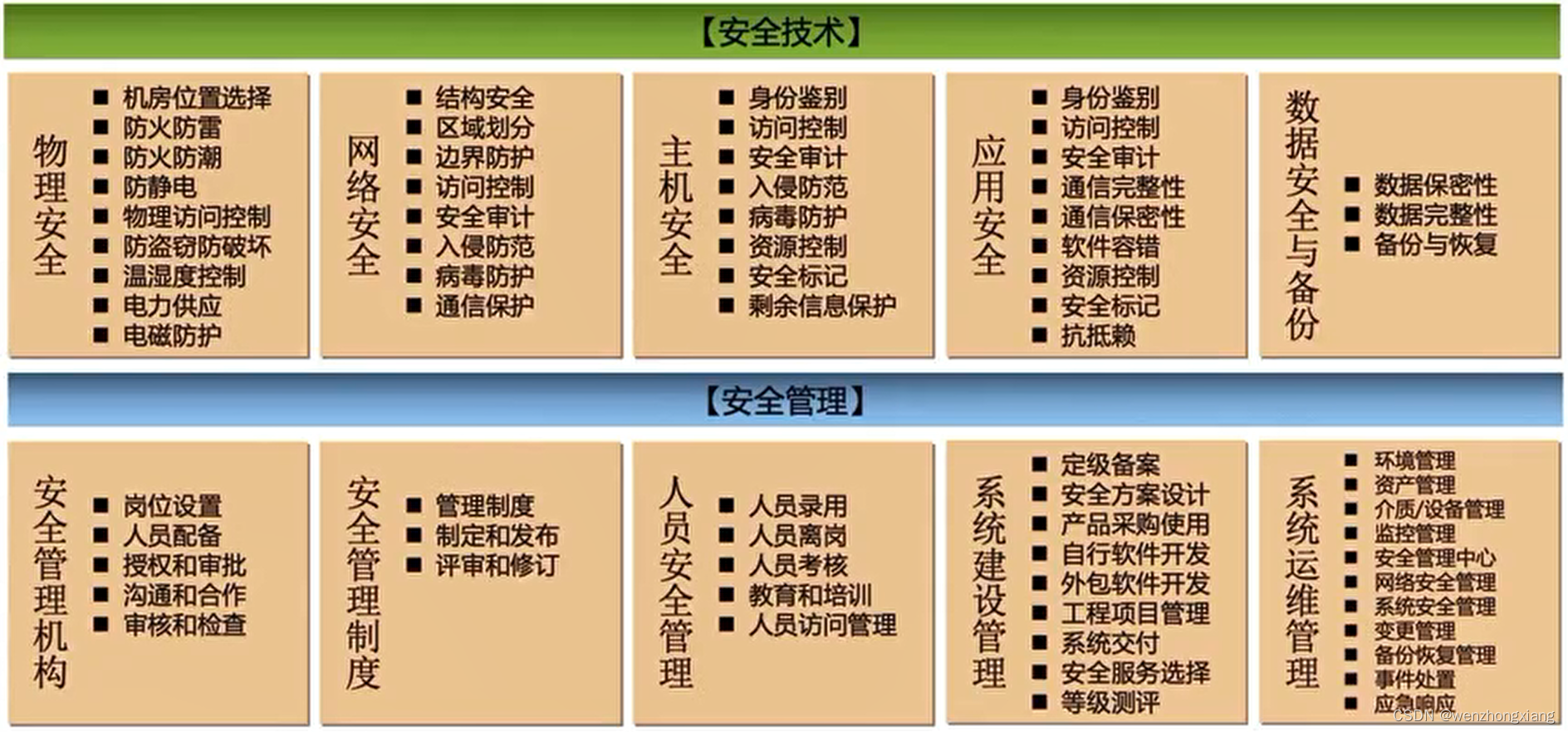
云安全之等级保护详解
等级保护概念 网络安全等级保护,是对信息系统分等级实行安全保护,对信息系统中使用的安全产品实行按等级管理,对信息系统中发生的信息安全事件分等级进行响应、处置。 网络安全等级保护的核心内容是:国家制定统一的政策、标准&a…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
