堆的初步认识
在学习本节文章前要先了解:大顶堆与小顶堆: (优先级队列_加瓦不加班的博客-CSDN博客)
堆实现
计算机科学中,堆是一种基于树的数据结构,通常用完全二叉树实现。
什么叫完全二叉树?
答:
1.除了最后一层不用满足有两个分支,其他层都要满足有两个分支
2.如果再往完全二叉树中加一个节点,那么必须靠左添加,从左往右依次填满,左边没有填满之前,右边就不能填,如图:
添加前:
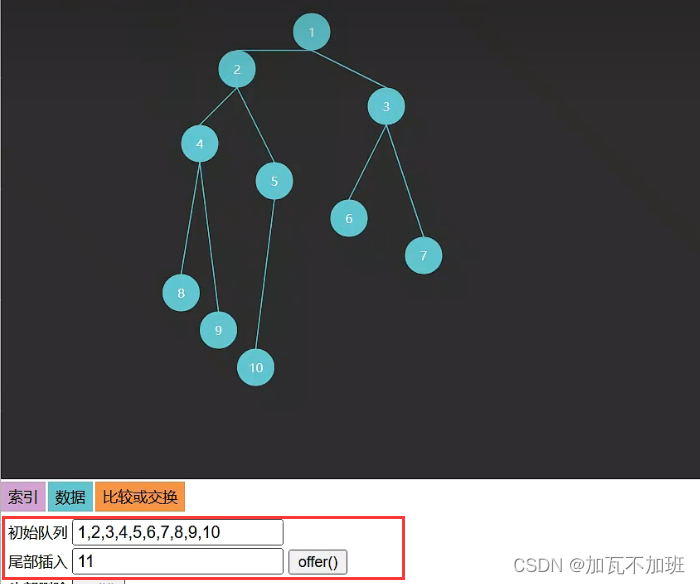
添加后:

堆的特性如下:堆分为两种:大顶堆与小顶堆
在大顶堆中,任意节点 C 与它的父节点 P 符合 P.value >= C.value:父节点的值>=子节点的值
而小顶堆中,任意节点 C 与它的父节点 P 符合 P.value <= C.value:父节点的值<=子节点的值
最顶层的节点(没有父亲)称之为 root 根节点
例1 - 满二叉树(Full Binary Tree)特点:每一层都是填满的

例2 - 完全二叉树(Complete Binary Tree)特点:最后一层可能未填满,靠左对齐

大顶堆
大顶堆中,任意节点 C 与它的父节点 P 符合 P.value >= C.value:父节点的值>=子节点的值
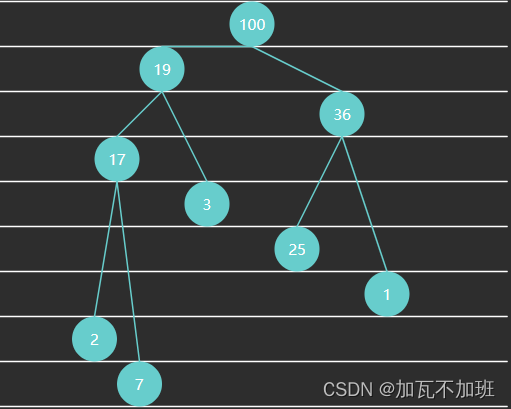
代码实现:
/*** @BelongsProject: arithmetic* @BelongsPackage: com.hzp.algorithm.heap* @Author: ASUS* @CreateTime: 2023-10-02 10:41* @Description: TODO 大顶堆Plus_增加了堆化等方法* @Version: 1.0*/
public class MaxHeap {int[] array;int size;public MaxHeap(int capacity) {this.array = new int[capacity];}/*** 获取堆顶元素** @return 堆顶元素*/public int peek() {//注意:当传入的数组是null时,我们可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行return array[0];}/*** 删除堆顶元素** @return 堆顶元素*/public int poll() {//注意:当传入的数组是null,可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行if(isEmpty()){throw new IllegalArgumentException("数组有问题");}int top = array[0];swap(0, size - 1);size--;//从索引位置0开始下潜down(0);return top;}private boolean isEmpty(){if(size==0){return true;}return false;}/*** 删除指定索引处元素 这个方法与删除堆顶元素方法思路一样** @param index 索引* @return 被删除元素*/public int poll(int index) {//注意:当传入的数组是null,可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行if(isEmpty()){throw new IllegalArgumentException("数组有问题");}int deleted = array[index];swap(index, size - 1);size--;down(index);return deleted;}/*** 替换堆顶元素* @param replaced 新元素*/public void replace(int replaced) {array[0] = replaced;down(0);}/*** 堆的尾部添加元素** @param offered 新元素* @return 是否添加成功*/public boolean offer(int offered) {if (size == array.length) {return false;}up(offered);size++;return true;}//向堆的尾部添加元素: 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶private void up(int offered) {int child = size;while (child > 0) {int parent = (child - 1) / 2;if (offered > array[parent]) {array[child] = array[parent];} else {break;}child = parent;}array[child] = offered;}public MaxHeap(int[] array) {this.array = array;this.size = array.length;heapify();}// 建堆private void heapify() {// 如何找到最后这个非叶子节点 :套用公式 size / 2 - 1for (int i = size / 2 - 1; i >= 0; i--) {down(i);}}// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大private void down(int parent) {int left = parent * 2 + 1;int right = left + 1;int max = parent;//left < size:必须是有效的索引 不可能超出数组最大长度吧if (left < size && array[left] > array[max]) {max = left;}if (right < size && array[right] > array[max]) {max = right;}if (max != parent) { // 找到了更大的孩子swap(max, parent);down(max);}}// 交换两个索引处的元素private void swap(int i, int j) {int t = array[i];array[i] = array[j];array[j] = t;}public static void main(String[] args) {
// int[] array = {1, 2, 3, 4, 5, 6, 7};
// MaxHeap maxHeap = new MaxHeap(array);
// System.out.println(Arrays.toString(maxHeap.array));//TODO 利用堆来实现排序//1. heapify 建立大顶堆//2. 将堆顶与堆底交换(最大元素被交换到堆底),缩小并下潜调整堆//3. 重复第二步直至堆里剩一个元素int[] array = {1, 2, 3, 4, 5, 6, 7};//1. heapify 建立大顶堆MaxHeap maxHeap = new MaxHeap(array);System.out.println(Arrays.toString(maxHeap.array));//3. 重复第二步直至堆里剩一个元素while(maxHeap.size>1){//将堆顶与堆底交换(最大元素被交换到堆底),缩小并下潜调整堆maxHeap.swap(0, maxHeap.size-1);maxHeap.size--;maxHeap.down(0);}System.out.println(Arrays.toString(maxHeap.array));}
}
小顶堆
小顶堆中,任意节点 C 与它的父节点 P 符合 P.value <= C.value:父节点的值<=子节点的值
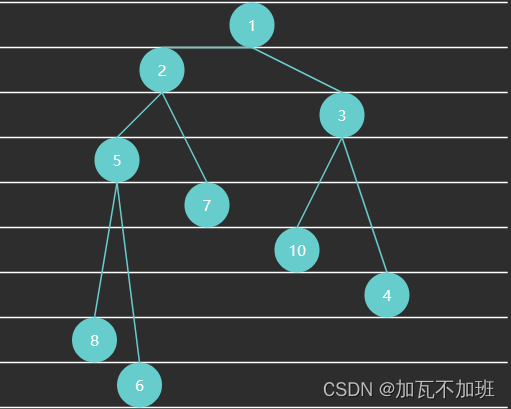
代码实现:
/*** @BelongsProject: arithmetic* @BelongsPackage: com.hzp.algorithm.heap* @Author: ASUS* @CreateTime: 2023-10-02 10:41* @Description: TODO 小顶堆Plus_增加了堆化等方法* @Version: 1.0*/
public class MinHeap {int[] array;int size;public MinHeap(int capacity) {this.array = new int[capacity];}/*** 获取堆顶元素** @return 堆顶元素*/public int peek() {//注意:当传入的数组是null时,我们可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行return array[0];}/*** 删除堆顶元素** @return 堆顶元素*/public int poll() {//注意:当传入的数组是null,可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行if(isEmpty()){throw new IllegalArgumentException("数组有问题");}int top = array[0];swap(0, size - 1);size--;//从索引位置0开始下潜down(0);return top;}private boolean isEmpty(){if(size==0){return true;}return false;}public boolean isFull(){return size==array.length;}/*** 删除指定索引处元素 这个方法与删除堆顶元素方法思路一样** @param index 索引* @return 被删除元素*/public int poll(int index) {//注意:当传入的数组是null,可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行if(isEmpty()){throw new IllegalArgumentException("数组有问题");}int deleted = array[index];swap(index, size - 1);size--;down(index);return deleted;}/*** 替换堆顶元素* @param replaced 新元素*/public void replace(int replaced) {array[0] = replaced;down(0);}/*** 堆的尾部添加元素** @param offered 新元素* @return 是否添加成功*/public boolean offer(int offered) {if (size == array.length) {return false;}up(offered);size++;return true;}//向堆的尾部添加元素: 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶private void up(int offered) {int child = size;while (child > 0) {int parent = (child - 1) / 2;if (offered < array[parent]) {array[child] = array[parent];} else {break;}child = parent;}array[child] = offered;}public MinHeap(int[] array) {this.array = array;this.size = array.length;heapify();}// 建堆private void heapify() {// 如何找到最后这个非叶子节点 :套用公式 size / 2 - 1for (int i = size / 2 - 1; i >= 0; i--) {down(i);}}// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大private void down(int parent) {int left = parent * 2 + 1;int right = left + 1;int min = parent;//left < size:必须是有效的索引 不可能超出数组最大长度吧if (left < size && array[left] < array[min]) {min = left;}if (right < size && array[right] < array[min]) {min = right;}if (min != parent) { // 找到了更大的孩子swap(min, parent);down(min);}}// 交换两个索引处的元素private void swap(int i, int j) {int t = array[i];array[i] = array[j];array[j] = t;}public static void main(String[] args) {
// int[] array = {1, 2, 3, 4, 5, 6, 7};
// MaxHeap maxHeap = new MaxHeap(array);
// System.out.println(Arrays.toString(maxHeap.array));//1. heapify 建立小顶堆//2. 将堆顶与堆底交换(最大元素被交换到堆底),缩小并下潜调整堆//3. 重复第二步直至堆里剩一个元素int[] array = {1, 2, 3, 4, 5, 6, 7};//1. heapify 建立大顶堆MinHeap maxHeap = new MinHeap(array);System.out.println(Arrays.toString(maxHeap.array));//3. 重复第二步直至堆里剩一个元素while(maxHeap.size>1){//将堆顶与堆底交换(最大元素被交换到堆底),缩小并下潜调整堆maxHeap.swap(0, maxHeap.size-1);maxHeap.size--;maxHeap.down(0);}System.out.println(Arrays.toString(maxHeap.array));}
}
完全二叉树可以使用数组来表示

那完全二叉树显然是个非线性的数据结构,但是它存储的时候可以使用线性的数组结构来存储数据:

特征
如果从索引 0 开始存储节点数据
节点 i 的父节点为 floor((i-1)/2),当 i>0 时
节点 i 的左子节点为 2i+1,右子节点为 2i+2,当然它们得 < size
如果从索引 1 开始存储节点数据
节点 i 的父节点为 floor(i/2),当 i > 1 时
节点 i 的左子节点为 2i,右子节点为 2i+1,同样得 < size
堆的优化
以大顶堆为例,相对于之前的优先级队列,增加了堆化等方法:
public class MaxHeap {int[] array;int size;public MaxHeap(int capacity) {this.array = new int[capacity];}/*** 获取堆顶元素** @return 堆顶元素*/public int peek() {//注意:当传入的数组是null时,我们可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行return array[0];}/*** 删除堆顶元素** @return 堆顶元素*/public int poll() {//注意:当传入的数组是null,可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行int top = array[0];swap(0, size - 1);size--;//从索引位置0开始下潜down(0);return top;}/*** 删除指定索引处元素 这个方法与删除堆顶元素方法思路一样** @param index 索引* @return 被删除元素*/public int poll(int index) {//注意:当传入的数组是null,可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行int deleted = array[index];swap(index, size - 1);size--;down(index);return deleted;}/*** 替换堆顶元素* @param replaced 新元素*/public void replace(int replaced) {array[0] = replaced;down(0);}/*** 堆的尾部添加元素** @param offered 新元素* @return 是否添加成功*/public boolean offer(int offered) {if (size == array.length) {return false;}up(offered);size++;return true;}//向堆的尾部添加元素: 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶private void up(int offered) {int child = size;while (child > 0) {int parent = (child - 1) / 2;if (offered > array[parent]) {array[child] = array[parent];} else {break;}child = parent;}array[child] = offered;}public MaxHeap(int[] array) {this.array = array;this.size = array.length;heapify();}// 建堆private void heapify() {// 如何找到最后这个非叶子节点 :套用公式 size / 2 - 1for (int i = size / 2 - 1; i >= 0; i--) {down(i);}}// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大private void down(int parent) {int left = parent * 2 + 1;int right = left + 1;int max = parent;//left < size:必须是有效的索引 不可能超出数组最大长度吧if (left < size && array[left] > array[max]) {max = left;}if (right < size && array[right] > array[max]) {max = right;}if (max != parent) { // 找到了更大的孩子swap(max, parent);down(max);}}// 交换两个索引处的元素private void swap(int i, int j) {int t = array[i];array[i] = array[j];array[j] = t;}public static void main(String[] args) {int[] array = {1, 2, 3, 4, 5, 6, 7};MaxHeap maxHeap = new MaxHeap(array);System.out.println(Arrays.toString(maxHeap.array));}
}Floyd 建堆算法作者(也是之前龟兔赛跑判环作者):
如果对龟兔赛跑判环不了解的可以查看此文章:

-
找到最后一个非叶子节点 (叶子节点:没有孩子的节点)
-
从后向前,对每个节点执行下潜
一些规律
-
一棵满二叉树节点个数为 2^h-1,如下例中高度 h=3 节点数是 2^3-1=7
-
非叶子节点范围为 [0, size/2-1]
算法时间复杂度分析

下面看交换次数的推导:设节点高度为 3

每一层的交换次数为:节点个数*此节点交换次数,总的交换次数为

即 h:总高度 i:本层高度

在 Wolfram|Alpha: Computational Intelligence 输入
Sum[\(40)Divide[Power[2,x],Power[2,i]]*\(40)i-1\(41)\(41),{i,1,x}]
推导出
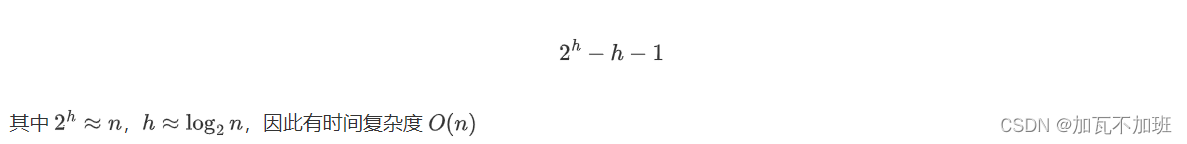
通用堆
通用heap :可以扩容的 heap, max 用于指定是大顶堆还是小顶堆
/*** @BelongsProject: arithmetic* @BelongsPackage: com.hzp.algorithm.heap* @Author: ASUS* @CreateTime: 2023-10-02 15:56* @Description: TODO 通用heap :可以扩容的 heap, max 用于指定是大顶堆还是小顶堆* @Version: 1.0*/
public class Heap {int[] array;int size;boolean max;public int size() {return size;}//当max为true则为大顶堆 如果是false则为小顶堆public Heap(int capacity, boolean max) {this.array = new int[capacity];this.max = max;}/*** 获取堆顶元素** @return 堆顶元素*/public int peek() {return array[0];}/*** 删除堆顶元素** @return 堆顶元素*/public int poll() {int top = array[0];swap(0, size - 1);size--;down(0);return top;}/*** 删除指定索引处元素** @param index 索引* @return 被删除元素*/public int poll(int index) {int deleted = array[index];swap(index, size - 1);size--;down(index);return deleted;}/*** 替换堆顶元素** @param replaced 新元素*/public void replace(int replaced) {array[0] = replaced;down(0);}/*** 堆的尾部添加元素** @param offered 新元素*/public void offer(int offered) {if (size == array.length) {grow();}up(offered);size++;}//如果容量不够就进行扩容private void grow() {int capacity = size + (size >> 1);int[] newArray = new int[capacity];//将原有的数组重新放到扩容好的数组中System.arraycopy(array, 0,newArray, 0, size);array = newArray;}// 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶private void up(int offered) {int child = size;while (child > 0) {int parent = (child - 1) / 2;boolean cmp = max ? offered > array[parent] : offered < array[parent];if (cmp) {array[child] = array[parent];} else {break;}child = parent;}array[child] = offered;}public Heap(int[] array, boolean max) {this.array = array;this.size = array.length;this.max = max;heapify();}// 建堆private void heapify() {// 如何找到最后这个非叶子节点 size / 2 - 1for (int i = size / 2 - 1; i >= 0; i--) {down(i);}}// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大private void down(int parent) {int left = parent * 2 + 1;int right = left + 1;int min = parent;if (left < size && (max ? array[left] > array[min] : array[left] < array[min])) {min = left;}if (right < size && (max ? array[right] > array[min] : array[right] < array[min])) {min = right;}if (min != parent) { // 找到了更大的孩子swap(min, parent);down(min);}}// 交换两个索引处的元素private void swap(int i, int j) {int t = array[i];array[i] = array[j];array[j] = t;}}
相关文章:
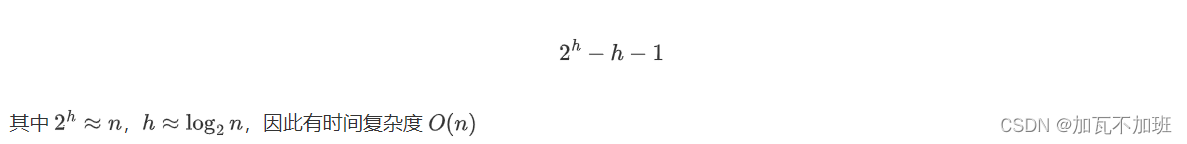
堆的初步认识
在学习本节文章前要先了解:大顶堆与小顶堆: (优先级队列_加瓦不加班的博客-CSDN博客) 堆实现 计算机科学中,堆是一种基于树的数据结构,通常用完全二叉树实现。 什么叫完全二叉树? 答&#x…...

CycleGAN模型之Pytorch实战
一、CycleGAN基本介绍 1. CycleGAN论文:《Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks》 2. 原文代码:https://github.com/junyanz/pytorch-CycleGAN-and-pix2pix 3. 网传精简代码:https://github.com/aitorzip/PyTorch-CycleGAN …...
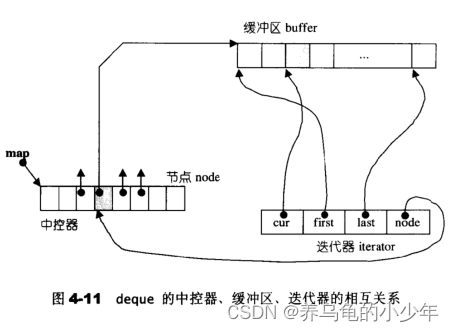
C++(STL容器适配器)
前言: 适配器也称配接器(adapters)在STL组件的灵活组合运用功能上,扮演着轴承、转换器的角色。 《Design Patterns》对adapter的定义如下:将一个class的接口转换为另一个class的接口,使原本因接口不兼容而…...
)
软考 系统架构设计师系列知识点之软件架构风格(7)
接前一篇文章:软考 系统架构设计师系列知识点之软件架构风格(6) 这个十一注定是一个不能放松、保持“紧”的十一。由于报名了全国计算机技术与软件专业技术资格(水平)考试,11月4号就要考试,因此…...

【Vue3】自定义指令
除了 Vue 内置的一系列指令 (比如 v-model 或 v-show) 之外,Vue 还允许你注册自定义的指令 (Custom Directives)。 1. 生命周期钩子函数 一个自定义指令由一个包含类似组件生命周期钩子的对象来定义。钩子函数会接收到指令所绑定元素作为其参数。 在 <script …...

UG\NX CAM二次开发 加工模块获取 UF _ask_application_module
文章作者:代工 来源网站:NX CAM二次开发专栏 简介: UG\NX CAM二次开发 加工模块获取 UF _ask_application_module 代码: void MyClass::do_it() { // TODO: add your code here // 获取NX当前所在的模块 int module_id = 0; // UF_ask_application_module(&…...

借助GPU算力编译Android
借助GPU算力编译Android 借助GPU编译Android代码的意义在于提高编译的效率和速度。传统的CPU编译方式在处理大量代码时可能会遇到性能瓶颈,而GPU编译利用了显卡的并行计算能力,可以同时处理多个任务,加快编译过程。通过利用GPU的并行计算能力,可以将编译过程中的多个任务分…...

docker-compose一键部署mysql
1.创建安装目录 mnt为硬盘挂载目录,根据实际情况修改 mkdir -p /mnt/mysql cd /mnt/mysql vim docker-compose.yml2.编写docker-compose.yml version: 3.1 services:db:image: mysql:5.7 #mysql版本volumes:- ./data/db:/var/lib/mysql #数据文件- ./etc/my.cnf:/…...
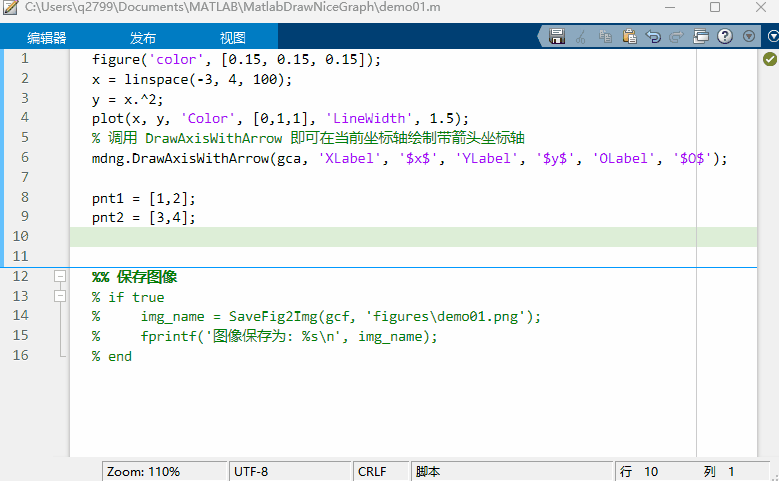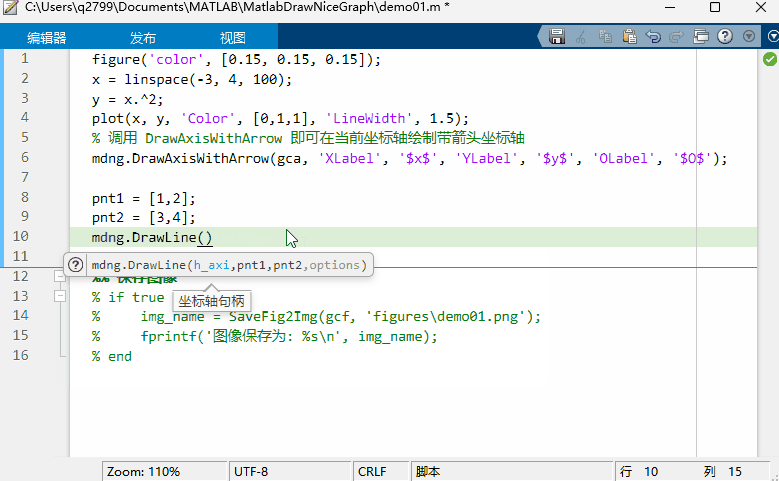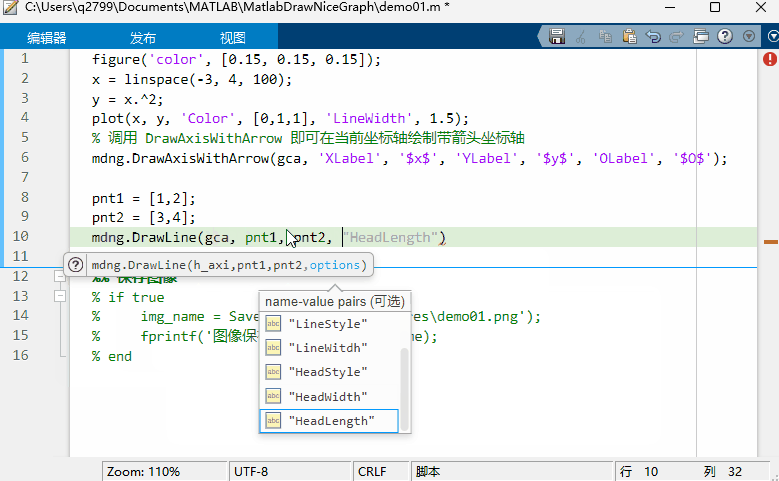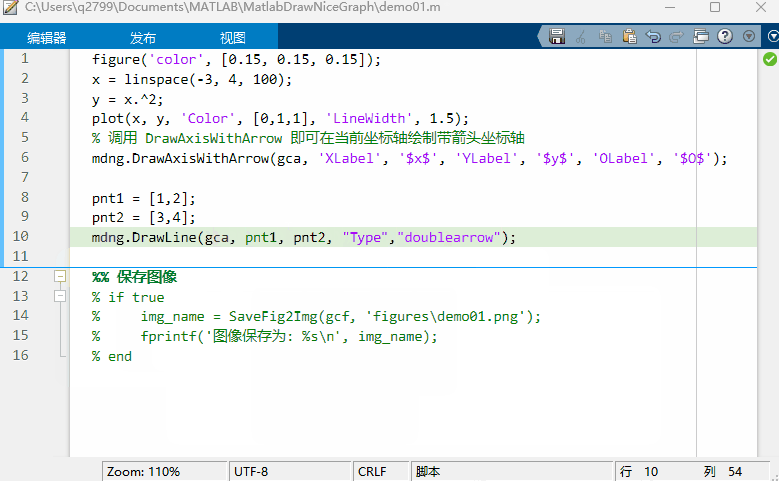
MATLAB 函数签名器
文章目录 MATLAB 函数签名器注释规范模板参数类型 kind数据格式 type选项的支持 使用可执行程序封装为m函数程序输出 编译待办事项推荐阅读附录 MATLAB 函数签名器 MATLAB 函数签名器 (FUNCSIGN) ,在规范注释格式的基础上为函数文件或类文件自动生成函数签名&#…...
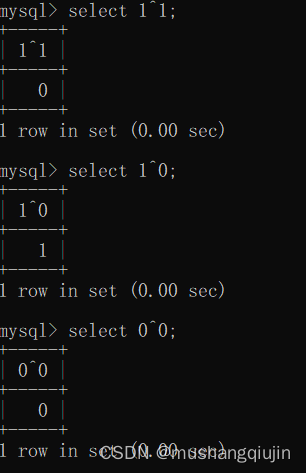
2019强网杯随便注bugktu sql注入
一.2019强网杯随便注入 过滤了一些函数,联合查询,报错,布尔,时间等都不能用了,尝试堆叠注入 1.通过判断是单引号闭合 ?inject1-- 2.尝试堆叠查询数据库 ?inject1;show databases;-- 3.查询数据表 ?inject1;show …...

Html+Css+Js计算时间差,返回相差的天/时/分/秒(从未来的一个日期时间到当前日期时间的差)。
Html部分 <!DOCTYPE html> <html><head><meta charset"utf-8" /><title></title><link rel"stylesheet" type"text/css" href"css/index.css" /><script src"js/index.js" t…...
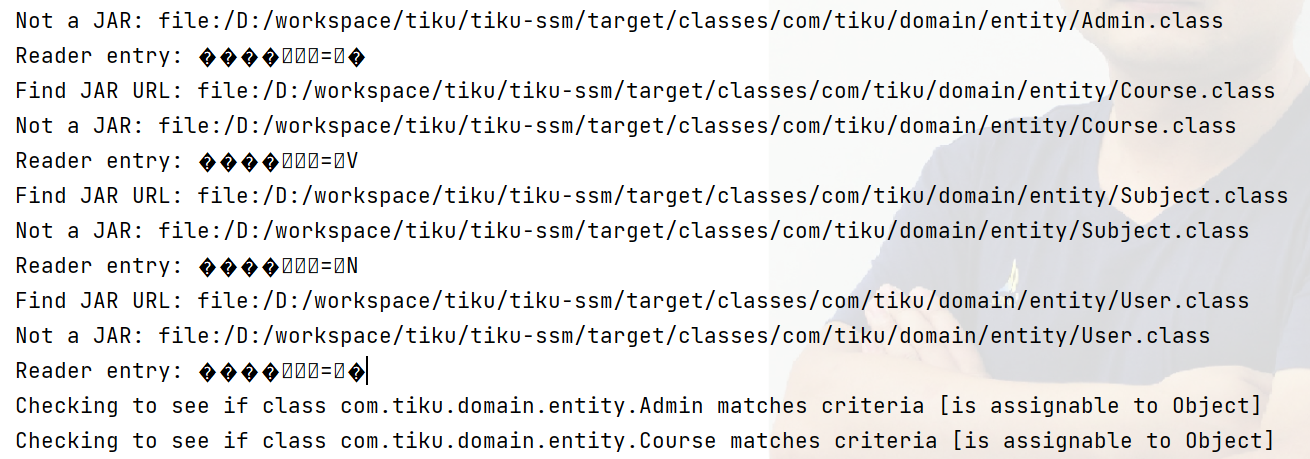
mybatis项目启动报错:reader entry: ���� = v
问题再现 解决方案一 由于指定的VFS没有找,mybatis启用了默认的DefaultVFS,然后由于DefaultVFS的内部逻辑,从而导致了reader entry乱码。 去掉mybatis配置文件中关于别名的配置,然后在mapper.xml文件中使用完整的类名。 待删除的…...

【GIT版本控制】--什么是版本控制
一、为什么需要版本控制? 版本控制是在软件开发和许多其他领域中非常重要的工具,因为它解决了许多与协作、追踪更改和管理项目相关的问题。以下是一些主要原因,解释了为什么需要版本控制: 追踪更改历史: 版本控制系统允许您准确…...

ChatGPT付费创作系统V2.3.4独立版 +WEB端+ H5端 + 小程序最新前端
人类小徐提供的GPT付费体验系统最新版系统是一款基于ThinkPHP框架开发的AI问答小程序,是基于国外很火的ChatGPT进行开发的Ai智能问答小程序。当前全民热议ChatGPT,流量超级大,引流不要太简单!一键下单即可拥有自己的GPT࿰…...

GEE16: 区域日均降水量计算
Precipitation 1. 区域日均降水量计算2. 降水时间序列3. 降水数据年度时间序列对比分析 1. 区域日均降水量计算 今天分析一个计算区域日均降水量的方法: 数据信息: Climate Hazards Group InfraRed Precipitation with Station data (CHIRPS) is a…...
打开MySQL数据库
在命令行里输入mysql --version就可以查看: mysql -uroot -p之前设置的密码(不用输入)就可登录成功:...
玩转ChatGPT:DALL·E 3生成图像
一、写在前面 好久不更新咯,因为没有什么有意思的东西分享的。 今天更新,是因为GPT整合了自家的图像生成工具,名字叫作DALLE 3。 DALLE 3是OpenAI推出的一种生成图像的模型,它基于GPT-3架构进行训练,但是它的主要目…...
小程序入门笔记(一) 黑马程序员前端微信小程序开发教程
微信小程序基本介绍 小程序和普通网页有以下几点区别: 运行环境:小程序可以在手机的操作系统上直接运行,如微信、支付宝等;而普通网页需要在浏览器中打开才能运行。 开发技术:小程序采用前端技术进行开发,…...
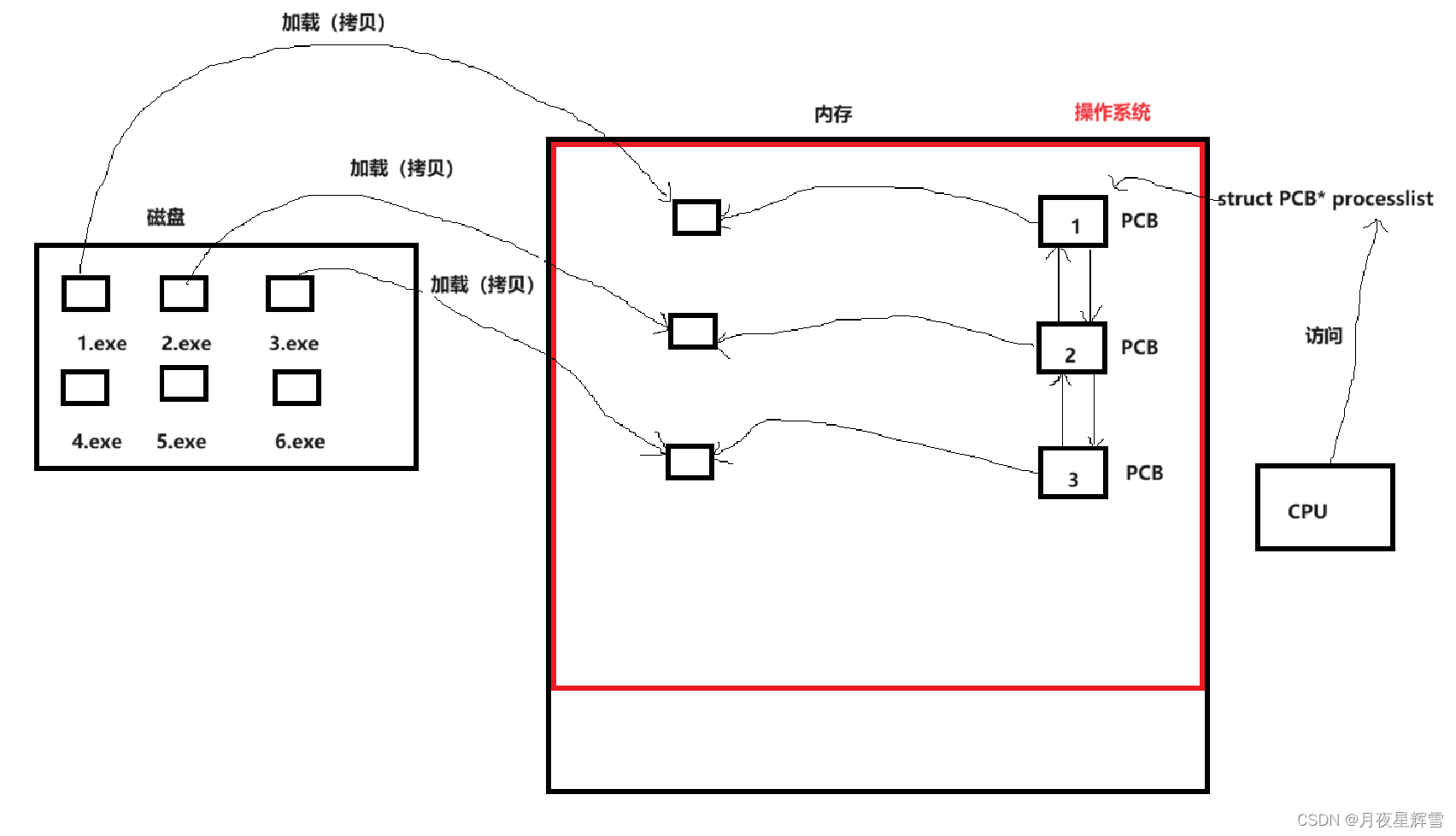
【进程管理】初识进程
一.何为进程 教材一般会给出这样的答案: 运行起来的程序 或者 内存中的程序 这样说太抽象了,那我问程序和进程有什么区别呢?诶?这我知道,书上说,动态的叫进程,静态的叫程序。那么静态和动态又是什么意思…...

ArcGIS Maps SDK for JS:监听按钮点击事件控制图层的visible属性
文章目录 1 需求描述2 解决方案 1 需求描述 现在有这么一个需求:在地图中添加一些图层,添加图层列表按钮。打开图层列表后用户会打开某些图层使其可见,要求关闭图层列表时,隐藏某些图层(若visibletrue) 2…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
