【算法|动态规划No.9】leetcodeLCR 091. 粉刷房子
个人主页:兜里有颗棉花糖
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创
收录于专栏【手撕算法系列专栏】【LeetCode】
🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望对大家有所帮助
🍓希望我们一起努力、成长,共同进步。
点击直接跳转到该题目
1️⃣题目描述
假如有一排房子,共 n 个,每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种,你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。
当然,因为市场上不同颜色油漆的价格不同,所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的正整数矩阵 costs 来表示的。
例如,costs[0][0] 表示第 0 号房子粉刷成红色的成本花费;costs[1][2] 表示第 1 号房子粉刷成绿色的花费,以此类推。
请计算出粉刷完所有房子最少的花费成本。
示例1:
输入: costs = [[17,2,17],[16,16,5],[14,3,19]]
输出: 10
解释: 将 0 号房子粉刷成蓝色,1 号房子粉刷成绿色,2 号房子粉刷成蓝色。
最少花费: 2 + 5 + 3 = 10。
示例2:
输入: costs = [[7,6,2]]
输出: 2
注意事项:
costs.length == ncosts[i].length == 31 <= n <= 1001 <= costs[i][j] <= 20
2️⃣题目解析
这里我们定义一个大小为(n + 1)* 3的二维dp表,之所以是n + 1是为了解决dp表的初始化问题(多出来的那个1我们可以将其理解为一个虚拟节点),具体解释如下:
- 为什么要使用大小为 (n+1) x 3 的数组呢?这是因为我们希望使用 dp[0] 表示第 0 个房屋(即没有房屋)的情况,而不是从 dp[1] 开始表示第一个房屋的情况。为了方便地处理边界情况,我们可以将数组的大小设置为 (n+1) x 3,从而在 dp[1] ~ dp[n] 中存储每个房屋对应的最小成本,而 dp[0] 可以被初始化为全0。
dp[i][0] 表示涂到第 i 房屋时,将其涂成红颜色的最小成本。
dp[i][1] 表示涂到第 i 房屋时,将其涂成蓝颜色的最小成本。
dp[i][2] 表示涂到第 i 房屋时,将其涂成绿颜色的最小成本。
状态转移方程如下:
dp[i][0] = min(dp[i-1][1],dp[i-1][2]) + costs[i - 1][0]dp[i][1] = min(dp[i-1][0],dp[i-1][2]) + costs[i - 1][1]dp[i][2] = min(dp[i-1][0],dp[i-1][1]) + costs[i - 1][2]
3️⃣解题代码
class Solution {
public:int minCost(vector<vector<int>>& costs) {int n = costs.size();vector<vector<int>> dp(n+1,vector<int>(3));for(int i = 1;i <= n;i++){dp[i][0] = min(dp[i-1][1],dp[i-1][2]) + costs[i-1][0];dp[i][1] = min(dp[i-1][0],dp[i-1][2]) + costs[i-1][1];dp[i][2] = min(dp[i-1][0],dp[i-1][1]) + costs[i-1][2];}return min(dp[n][0],min(dp[n][1],dp[n][2]));}
};
通过啦:
相关文章:

【算法|动态规划No.9】leetcodeLCR 091. 粉刷房子
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【LeetCode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…...
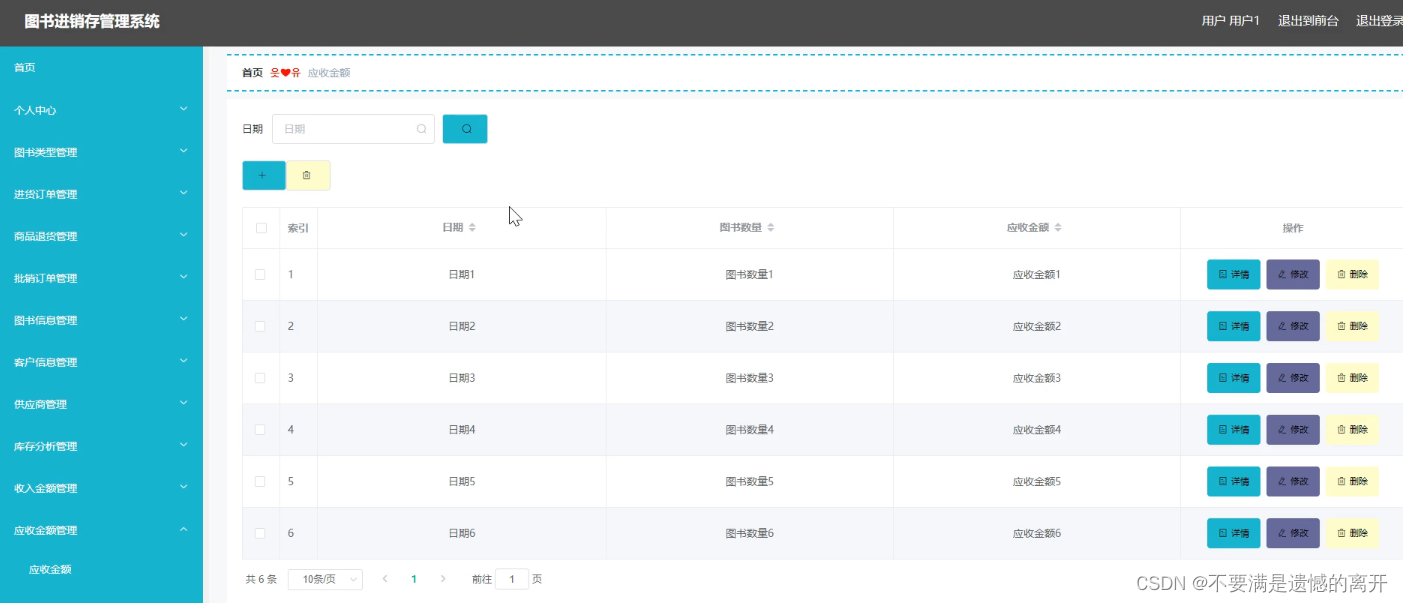
基于SpringBoot的图书进销存管理系统
目录 前言 一、技术栈 二、系统功能介绍 用户信息管理 图书类型管理 商品退货管理 客户信息管理 图书添加 客户添加 应收金额 三、核心代码 1、登录模块 2、文件上传模块 3、代码封装 前言 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实…...

回归预测 | MATLAB实现PSO-SVR粒子群优化支持向量机回归多输入单输出预测
回归预测 | MATLAB实现PSO-SVR粒子群优化支持向量机回归多输入单输出预测 目录 回归预测 | MATLAB实现PSO-SVR粒子群优化支持向量机回归多输入单输出预测预测效果基本介绍模型描述程序设计预测效果 <...

vue3使用v-model控制子组件进行双向数据绑定
vue2写法: 中父组件调用子组件: <child :isShow.sync"isShow" v-show"isShow"/> 子组件想要消失, 在子组件写: this.$emit("update:isShow",false); 具体代码就不粘贴了 vue3写法: 父组件核心代码: v-model:a"xxx" 子组…...

.netCore .net5,6,7 存日志文件
如果你使用 .netCore及以上版本(.net5,.net6,.net7)... 系统默认自带日志中间件(log4net) 对,就是上次java 日志大漏洞的兄弟....... 控制台自动打印日志就是它的功劳 现在我们想存日志文件,怎么办 很简单. 1.在项目中添加日志配置文件 文件名 : log4net.config 不能…...
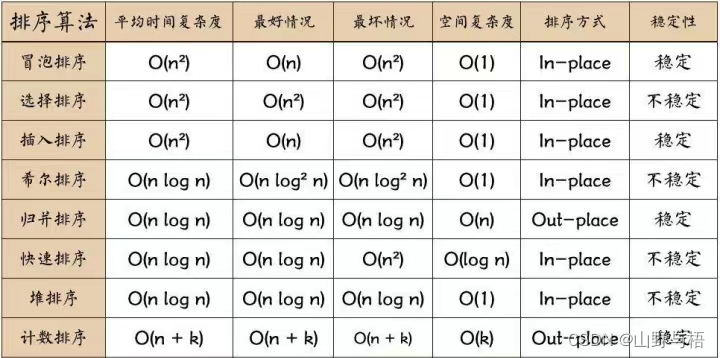
【数据结构---排序】很详细的哦
本篇文章介绍数据结构中的几种排序哦~ 文章目录 前言一、排序是什么?二、排序的分类 1.直接插入排序2.希尔排序3.选择排序4.冒泡排序5.快速排序6.归并排序总结 前言 排序在我们的生活当中无处不在,当然,它在计算机程序当中也是一种很重要的操…...
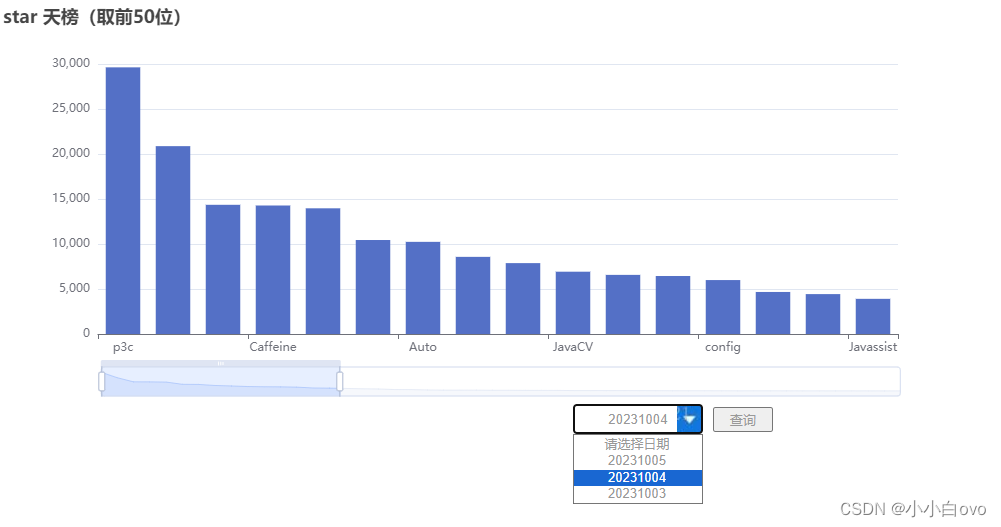
GitHub爬虫项目详解
前言 闲来无事浏览GitHub的时候,看到一个仓库,里边列举了Java的优秀开源项目列表,包括说明、仓库地址等,还是很具有学习意义的。但是大家也知道,国内访问GitHub的时候,经常存在访问超时的问题,…...
-NOA领航辅助系统-上汽荣威)
辅助驾驶功能开发-功能对标篇(7)-NOA领航辅助系统-上汽荣威
1.横向对标参数 厂商上汽荣威车型荣威RX5(燃油车)上市时间2022Q3方案10V3R摄像头前视摄像头1*(8M)侧视摄像头4后视摄像头1环视摄像头4DMS摄像头1雷达毫米波雷达34D毫米波雷达/超声波雷达12激光雷达/域控供应商1*(宏景智驾)辅助驾驶软件供应商地平线高精度地图中海庭芯片J3合作…...

第0次 序言
突然想起有好多书没有看,或者看了也没留下任何记录,以后有空必须得好好整理才行,这次就从《Linux命令行和shell脚本编程大全开始》 本文完全是闲聊,自娱自乐,我觉得做开发是一件很快乐的事情,但是工作是开发…...

ESP32设备驱动-OLED显示单个或多个DS18B20传感器数据
OLED显示单个或多个DS18B20传感器数据 文章目录 OLED显示单个或多个DS18B20传感器数据1、DS18B20介绍2、硬件准备3、软件准备4、代码实现4.1 读取单个DS18B20数据4.2 驱动多个DS18B20传感器4.3 OLED显示DS18B20数据在本文中,我们将介绍如何ESP32驱动单个或多个DS18B20传感器,…...
MongoDB快速上手
文章目录 1、mongodb相关概念1.1、业务应用场景1.2、MongoDB简介1.3、体系结构1.3.1 数据库 (databases) 管理语法1.3.2 集合 (collection) 管理语法 1.4、数据模型1.5、MongoDB的特点 2、单机部署3、基本常用命令3.1、案例需求3.2、数据库操作3.2.1 选择和创建数据库3.2.2 数据…...
maven 初学
1. maven 安装 配置安装 路径 maven 下载位置: D:\software\apache-maven-3.8.6 默认仓库位置: C:\Users\star-dream\.m2\repository 【已更改】 本地仓库设置为:D:\software\apache-maven-3.8.6\.m2\repository 镜像已更改为阿里云中央镜像仓库 <mirrors>…...
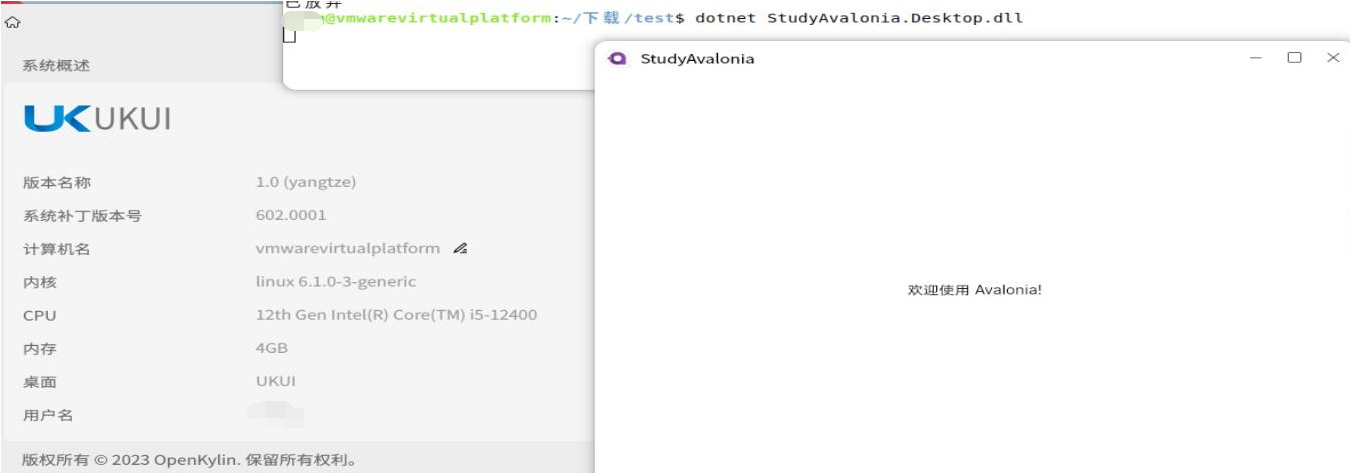
解决WPF+Avalonia在openKylin系统下默认字体问题
一、openKylin简介 openKylin(开放麒麟) 社区是在开源、自愿、平等和协作的基础上,由基础软硬件企业、非营利性组织、社团组织、高等院校、科研机构和个人开发者共同创立的一个开源社区,致力于通过开源、开放的社区合作ÿ…...
智能合约漏洞,Dyna 事件分析
智能合约漏洞,Dyna 事件分析 1. 漏洞简介 https://twitter.com/BlockSecTeam/status/1628319536117153794 https://twitter.com/BeosinAlert/status/1628301635834486784 2. 相关地址或交易 攻击交易 1: https://bscscan.com/tx/0x7fa89d869fd1b89e…...
:Elasticsearch7.x的官方文档学习(Set up Elasticsearch))
Elasticsearch基础篇(四):Elasticsearch7.x的官方文档学习(Set up Elasticsearch)
Set up Elasticsearch 1 Configuring Elasticsearch(配置 Elasticsearch)1.1 Setting JVM Options(设置JVM选项)1.2 Secure Settings(安全设置)Introduction(介绍)Using the Keystore(使用密钥库)Applying Changes(应用更改)Reloadable Secure Settings(可重新加载的安全设置)R…...
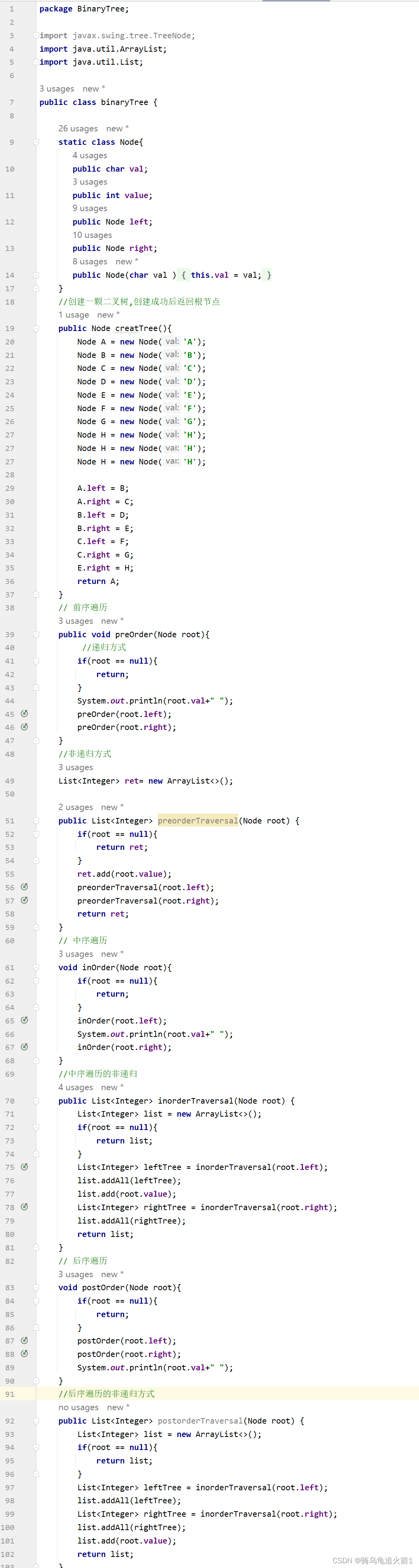
二叉树的遍历方式和代码
二叉树的三种遍历和代码 1.前序遍历2.中序遍历3.后序遍历4.三种遍历方式的代码实现 1.前序遍历 学习二叉树结构,最简单的方式就是遍历。所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具…...

小样本学习——匹配网络
目录 匹配网络 (1)简单介绍: (2)专业术语 (3)主要思想 (4)训练过程 问题 回答 MANN 匹配网络 (1)简单介绍: Matching netwo…...

CSS 常用样式 之字体属性
font-weight(字体粗细) 字体粗细用于设置文本的粗细程度,可以使用如下的值: normal:正常字体(默认)bold:加粗字体bolder:更加加粗lighter:更加细 代码实例…...
nodejs+vue游戏测评交流系统elementui
可以实现首页、发布招募、公司资讯、我的等,另一方面来说也可以提高在游戏测评交流方面的效率给相关管理人员的工作带来一定的便利。在我的页面可以对游戏攻略、我的收藏管理、实际上如今信息化成为一个未来的趋势或者可以说在当前现代化的城市典范中,发布招募等功能…...

1.2.OpenCV技能树--第一单元--OpenCV安装
目录 1.文章内容来源 2.OpenCV安装 3.课后习题代码复现 4.易错点总结与反思 1.文章内容来源 1.题目来源:https://edu.csdn.net/skill/opencv/opencv-662dbd65c89d4ddb9e392f44ffe16e1a?category657 2.资料来源:https://edu.csdn.net/skill/opencv/opencv-662dbd65c89d4ddb…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...

