2.证明 非单一点 Oct.2023
目录
- 原题
- 解
- 引申出的编程问题
- 非单一点
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 题解
- 题目
- 正解
原题
已知等边 Δ P 0 P 1 P 2 \Delta P_0P_1P_2 ΔP0P1P2,它的外接圆是 O O O,设 O O O的半径是 R R R。同时,设 Δ P 0 P 1 P 2 \Delta P_0P_1P_2 ΔP0P1P2所经过的所有点的集合是 S 0 S_0 S0。显然, S 0 S_0 S0中有无限个元素。
接下来,在 O O O上取点 P 3 , P 4 , P 5 P_3,P_4,P_5 P3,P4,P5,使得四边形 P 0 P 3 P 4 P 5 P_0P_3P_4P_5 P0P3P4P5是正四边形。记这个四边形经过的所有点的集合为 S 1 S_1 S1。
接下来,在 O O O上取点 P 6 , P 7 , P 8 , P 9 P_6,P_7,P_8,P_9 P6,P7,P8,P9,使得五边形 P 0 P 6 P 7 P 8 P 9 P_0P_6P_7P_8P_9 P0P6P7P8P9是正五边形。记这个五边形的点集为 S 2 S_2 S2。
中间省略 n − 2 n-2 n−2次操作。
最后,在 O O O上取点 δ 1 , δ 2 , δ 3 , . . . , δ n \delta_1,\delta_2,\delta_3,...,\delta_n δ1,δ2,δ3,...,δn,使得 n + 1 n+1 n+1边形 P 0 δ 1 δ 2 δ 3 . . . δ n P_0\delta_1\delta_2\delta_3...\delta_n P0δ1δ2δ3...δn是正 n + 1 n+1 n+1边形。
记所有 P 0 δ 1 δ 2 δ 3 . . . δ n P_0\delta_1\delta_2\delta_3...\delta_n P0δ1δ2δ3...δn上的非单一点的集合为 W ′ W' W′。
非单一点的定义是:
-
对于每一个点, S 0 , S 1 , . . . , S n − 1 S_0,S_1,...,S_{n-1} S0,S1,...,Sn−1中任意一个集合包含了它
-
设这个点的坐标是 x , y x,y x,y,则 x , y x,y x,y满足 x 2 + y 2 = R 2 x^2+y^2=R^2 x2+y2=R2
显然, P 0 P_0 P0是一个非单一点。
记 W ′ W' W′中元素的个数为 L ′ L' L′。
回答下列问题:
(1)当 n = 9 n=9 n=9时,求 L ′ L' L′;
(2)当 n = 99 n=99 n=99时,求 L ′ L' L′;
(3)证明或证伪: n n n有无限种取值方法,使得 L ′ = 1 L'=1 L′=1;
(4)求 2 1.048576 × 1 0 6 2^{1.048576\times 10^6} 21.048576×106边形与 3 3 27 3^{3^{27}} 3327的公共点数。
(5)证明或证伪:并非对于所有的 n = 2 2 x n=2^{2^x} n=22x,都存在 L ′ = 1 L'=1 L′=1。
解
让我们先单独讨论 M M M边形的情况。
不妨设 M M M边形的 M M M个点分别为 P 0 , P 1 , . . . , P M − 1 P_0,P_1,...,P_{M-1} P0,P1,...,PM−1,且外接圆心为 O O O,半径为 R R R。
定义 ∠ P i O P 0 = θ i \angle P_iOP_0=\theta_i ∠PiOP0=θi,设 P 0 ( R , 0 ) P_0(R,0) P0(R,0)。
则有 θ i = 2 π i M \theta_i=\frac{2\pi i}{M} θi=M2πi。
那么我们可以求出
P i ( x i , y i ) x i = R cos θ i , y i = R sin θ i . P_i(x_i,y_i)\\ x_i=R\cos\theta_i,\\ y_i=R\sin\theta_i. Pi(xi,yi)xi=Rcosθi,yi=Rsinθi.
那么我们回到原题。
由于非单一点的第二个条件,我们得知它在圆 O O O上。
不妨设 N N N边形( N = n + 1 N=n+1 N=n+1)的第 i i i个点与 K K K边形的第 j j j个点重合。
那么我们有:
θ i = θ j + 2 k π 2 π i N = 2 π j K + 2 k π , 1 ≤ j < K < N , i < N i N = j K + k ∵ 0 ≤ i N < 1 , 0 ≤ j K < 1 ∴ k = 0 ∴ j N = i K , i = j N K \theta_i=\theta_j+2k\pi\\ \frac{2\pi i}{N}=\frac{2\pi j}{K}+2k\pi,1\leq j<K<N,i < N \\ \frac{i}{N}=\frac{j}{K}+k\\ \because 0\leq\frac{i}{N}<1,0\leq\frac{j}{K}<1\\ \therefore k=0\\ \therefore jN=iK,i=j\frac{N}{K} \\ θi=θj+2kπN2πi=K2πj+2kπ,1≤j<K<N,i<NNi=Kj+k∵0≤Ni<1,0≤Kj<1∴k=0∴jN=iK,i=jKN
例如,当 n = 9 n=9 n=9时, N = n + 1 = 10 N=n+1=10 N=n+1=10,符合的结果有:
i = 0 , c h o o s e j = 0 i = 1 , N o W a y i = 2 , c h o o s e j = 1 , K = 5 i = 3 , N o W a y i = 4 , c h o o s e j = 2 , K = 5 i = 5 , c h o o s e j = 2 , K = 4 i = 6 , c h o o s e j = 3 , K = 5 i = 7 , N o W a y i = 8 , c h o o s e j = 4 , K = 5 i = 9 , N o W a y i=0,choose\ j=0\\ i=1,No\ Way\\ i=2,choose\ j=1,K=5\\ i=3,No\ Way\\ i=4,choose\ j=2,K=5\\ i=5,choose\ j=2,K=4\\ i=6,choose\ j=3,K=5\\ i=7,No\ Way\\ i=8,choose\ j=4,K=5\\ i=9,No\ Way i=0,choose j=0i=1,No Wayi=2,choose j=1,K=5i=3,No Wayi=4,choose j=2,K=5i=5,choose j=2,K=4i=6,choose j=3,K=5i=7,No Wayi=8,choose j=4,K=5i=9,No Way
第一问答案为 6 6 6。
假设 N = β 1 α 1 β 2 α 2 . . . β n α n , β i < β j w h e n i ≤ j , N=\beta_1^{\alpha_1}\beta_2^{\alpha_2}...\beta_n^{\alpha_n},\beta_i<\beta_j\ when\ i\leq j, N=β1α1β2α2...βnαn,βi<βj when i≤j,且 β i \beta_i βi为质数。
显然 i = p M i=pM i=pM,且 M = β i β j . . . M=\beta_i\beta_j... M=βiβj...( β i \beta_i βi可能与 β j , . . . \beta_j,... βj,...相等)
则有 j = p , K = N M j=p,K=\frac{N}{M} j=p,K=MN。
显然 K < N K<N K<N,那么只需得 p < N M p<\frac NM p<MN。
对于 N = 100 N=100 N=100的情况,
N = 2 2 ⋅ 5 2 = 2 ⋅ 2 ⋅ 5 ⋅ 5 N=2^2·5^2=2·2·5·5 N=22⋅52=2⋅2⋅5⋅5
i = 1 × 2 = 2 , 2 × 2 = 4 , . . . , 49 × 2 = 98. 1 × 5 = 5 , 2 × 5 = 10 , . . . , 19 × 5 = 95. i=\\ 1\times 2=2,\\ 2\times 2=4,\\ ...,\\ 49\times 2=98.\\ \\ 1\times 5=5,\\ 2\times 5=10,\\ ...,\\ 19\times 5=95. i=1×2=2,2×2=4,...,49×2=98.1×5=5,2×5=10,...,19×5=95.
在这些点中,有 9 9 9种重复的情况。因此得到结果为 49 + 19 − 9 + 1 = 60 49+19-9+1=60 49+19−9+1=60种。(还要加上 P 0 P_0 P0)
总结规律,发现实质上就是求 N N N所有的不与它互质且小于它自己的数。注意 N > 4 N>4 N>4,因为图里面没有二边形
那么对于每一个质数,显然 L ′ L' L′只能为 1 1 1。而质数有无限个,那么第三问得证。
对于第四问,显然这两个数互质,没有重复的点。
对于第五问,存在许多反例,其中一个就是 n = 5 n=5 n=5,此时的 N N N不是质数,则必定存在除 P 0 P_0 P0外的非单一点。
引申出的编程问题
Non-Single Points
如下。
非单一点
题目描述
已知等边 Δ P 0 P 1 P 2 \Delta P_0P_1P_2 ΔP0P1P2,它的外接圆是 O O O,设 O O O的半径是 R R R。同时,设 Δ P 0 P 1 P 2 \Delta P_0P_1P_2 ΔP0P1P2所经过的所有点的集合是 S 0 S_0 S0。显然, S 0 S_0 S0中有无限个元素。
接下来,在 O O O上取点 P 3 , P 4 , P 5 P_3,P_4,P_5 P3,P4,P5,使得四边形 P 0 P 3 P 4 P 5 P_0P_3P_4P_5 P0P3P4P5是正四边形。记这个四边形经过的所有点的集合为 S 1 S_1 S1。
接下来,在 O O O上取点 P 6 , P 7 , P 8 , P 9 P_6,P_7,P_8,P_9 P6,P7,P8,P9,使得五边形 P 0 P 6 P 7 P 8 P 9 P_0P_6P_7P_8P_9 P0P6P7P8P9是正五边形。记这个五边形的点集为 S 2 S_2 S2。
中间省略 n − 2 n-2 n−2次操作。
最后,在 O O O上取点 δ 1 , δ 2 , δ 3 , . . . , δ n \delta_1,\delta_2,\delta_3,...,\delta_n δ1,δ2,δ3,...,δn,使得 n + 1 n+1 n+1边形 P 0 δ 1 δ 2 δ 3 . . . δ n P_0\delta_1\delta_2\delta_3...\delta_n P0δ1δ2δ3...δn是正 n + 1 n+1 n+1边形。
记所有 P 0 δ 1 δ 2 δ 3 . . . δ n P_0\delta_1\delta_2\delta_3...\delta_n P0δ1δ2δ3...δn上的非单一点的集合为 W ′ W' W′。
非单一点的定义是:
-
对于每一个点, S 0 , S 1 , . . . , S n − 1 S_0,S_1,...,S_{n-1} S0,S1,...,Sn−1中任意一个集合包含了它
-
设这个点的坐标是 x , y x,y x,y,则 x , y x,y x,y满足 x 2 + y 2 = R 2 x^2+y^2=R^2 x2+y2=R2
显然, P 0 P_0 P0是一个非单一点。
记 W ′ W' W′中元素的个数为 L ′ L' L′。
输入格式
T T T组数据。
每一组数据只有一行,输入 n n n。
输出格式
T T T行,按顺序输出每个样例的 L ′ L' L′。
样例 #1
样例输入 #1
1
9
样例输出 #1
6
提示
对于 100 % 100\% 100%的数据,有 7 < n < 5 × 1 0 6 7<n<5\times10^6 7<n<5×106, 1 ≤ T < 5 × 1 0 6 1\leq T<5\times10^6 1≤T<5×106。
题解
传送门
如下。
题目
传送门
正解
单独讨论 M M M边形的情况。
不妨设 M M M边形的 M M M个点分别为 P 0 , P 1 , . . . , P M − 1 P_0,P_1,...,P_{M-1} P0,P1,...,PM−1,且外接圆心为 O O O,半径为 R R R。
定义 ∠ P i O P 0 = θ i \angle P_iOP_0=\theta_i ∠PiOP0=θi,设 P 0 ( R , 0 ) P_0(R,0) P0(R,0)。
则有 θ i = 2 π i M \theta_i=\frac{2\pi i}{M} θi=M2πi。
那么我们可以求出
P i ( x i , y i ) P_i(x_i,y_i) Pi(xi,yi)
x i = R cos θ i , x_i=R\cos\theta_i, xi=Rcosθi,
y i = R sin θ i . y_i=R\sin\theta_i. yi=Rsinθi.
那么我们回到原题。
由于非单一点的第二个条件,我们得知它在圆 O O O上。
不妨设 N N N边形( N = n + 1 N=n+1 N=n+1)的第 i i i个点与 K K K边形的第 j j j个点重合。
那么我们有:
θ i = θ j + 2 k π \theta_i=\theta_j+2k\pi θi=θj+2kπ
2 π i N = 2 π j K + 2 k π , 1 ≤ j < K < N , i < N \frac{2\pi i}{N}=\frac{2\pi j}{K}+2k\pi,1\leq j<K<N,i < N N2πi=K2πj+2kπ,1≤j<K<N,i<N
i N = j K + k \frac{i}{N}=\frac{j}{K}+k Ni=Kj+k
∵ 0 ≤ i N < 1 , 0 ≤ j K < 1 \because 0\leq\frac{i}{N}<1,0\leq\frac{j}{K}<1 ∵0≤Ni<1,0≤Kj<1
∴ k = 0 \therefore k=0 ∴k=0
∴ j N = i K , i = j N K \therefore jN=iK,i=j\frac{N}{K} ∴jN=iK,i=jKN
例如,当 n = 9 n=9 n=9时, N = n + 1 = 10 N=n+1=10 N=n+1=10,符合的结果有:
i = 0 , c h o o s e j = 0 i=0,choose\ j=0 i=0,choose j=0
i = 1 , N o W a y i=1,No\ Way i=1,No Way
i = 2 , c h o o s e j = 1 , K = 5 i=2,choose\ j=1,K=5 i=2,choose j=1,K=5
i = 3 , N o W a y i=3,No\ Way i=3,No Way
i = 4 , c h o o s e j = 2 , K = 5 i=4,choose\ j=2,K=5 i=4,choose j=2,K=5
i = 5 , c h o o s e j = 2 , K = 4 i=5,choose\ j=2,K=4 i=5,choose j=2,K=4
i = 6 , c h o o s e j = 3 , K = 5 i=6,choose\ j=3,K=5 i=6,choose j=3,K=5
i = 7 , N o W a y i=7,No\ Way i=7,No Way
i = 8 , c h o o s e j = 4 , K = 5 i=8,choose\ j=4,K=5 i=8,choose j=4,K=5
i = 9 , N o W a y i=9,No\ Way i=9,No Way
样例答案为 6 6 6。
假设 N = β 1 α 1 β 2 α 2 . . . β n α n , β i < β j w h e n i ≤ j , N=\beta_1^{\alpha_1}\beta_2^{\alpha_2}...\beta_n^{\alpha_n},\beta_i<\beta_j\ when\ i\leq j, N=β1α1β2α2...βnαn,βi<βj when i≤j,且 β i \beta_i βi为质数。
显然 i = p M i=pM i=pM,且 M = β i β j . . . M=\beta_i\beta_j... M=βiβj...( β i \beta_i βi可能与 β j , . . . \beta_j,... βj,...相等)
则有 j = p , K = N M j=p,K=\frac{N}{M} j=p,K=MN。
显然 K < N K<N K<N,那么只需得 p < N M p<\frac NM p<MN。
那么我们就能发现非单一点的数量 L ′ L' L′实质上是所有小于 N N N且不与 N N N互质的数字的数量再加一。
统计与 N N N互质的数字可以借助于欧拉函数。
介绍
AC代码:
#include <iostream>
#include <cstring>
using namespace std;
const int N = (int)5e6;
int a[N];
inline void read(int &x) { // 返回类型必须为void,否则竞赛中Linux测评会报错,Windows没事x = 0;short flag = 1;char c = getchar();while(c < '0' || c > '9'){// 此处如果只用if的话容易在数据不规范时出错,特别是cin和read混用if(c == '-')flag = -1;c = getchar();}while(c >= '0' && c <= '9') {x = (x << 3) + (x << 1) + (c ^ 48); // 48这个数字恰好往后10个数都可以使用位运算,可以写成二进制证明;位运算能用当然更好c = getchar();}x *= flag;
}
/*
inline int read()
{int X = 0, w = 0; char ch = 0;while (!isdigit(ch)) { w |= ch == '-'; ch = getchar(); }while (isdigit(ch)) X = (X << 3) + (X << 1) + (ch ^ 48), ch = getchar();return w ? -X : X;
}
*/ inline void write(int x)
{if (x < 0) putchar('-'), x = -x;if (x > 9) write(x / 10);putchar(x % 10 + '0');
}void phi_table() //打表,求出1500000中所有的数的欧拉函数值
{memset(a,0,sizeof(a));a[1]=1;for(register int i=2;i<=N;++i)if(!a[i]){for(register int j=i;j<=N;j+=i){if(!a[j])a[j]=j;a[j]=a[j]/i*(i-1);}}
}
int main(){int T,n;read(T);phi_table();while (T--) {read(n);write(n+1-a[n+1]);putchar('\n');}return 0;
}
相关文章:

2.证明 非单一点 Oct.2023
目录 原题解引申出的编程问题非单一点题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示 题解题目正解 原题 已知等边 Δ P 0 P 1 P 2 \Delta P_0P_1P_2 ΔP0P1P2,它的外接圆是 O O O,设 O O O的半径是 R R R。同时,设 Δ …...
常见的软件脱壳思路
单步跟踪法 1.本方法采用OD载入。 2.跟踪F8,实现向下的跳。 3.遇到程序回跳按F4。 4.绿色线条表示跳转没实现,不用理会,红色线条表示跳转已经实现! 5.刚载入程序有一个CALL的,我们就F7跟进去,不然程序很容…...
, torch.nn.Conv2d()和torch.nn.Conv3d()函数理解)
Python:torch.nn.Conv1d(), torch.nn.Conv2d()和torch.nn.Conv3d()函数理解
Python:torch.nn.Conv1d(), torch.nn.Conv2d()和torch.nn.Conv3d()函数理解 1. 函数参数 在torch中的卷积操作有三个,torch.nn.Conv1d(),torch.nn.Conv2d()还有torch.nn.Conv3d(),这是搭建网络过程中常用的网络层,为了用好卷积层࿰…...

scala 连接 MySQL 数据库案例
1 依赖准备 mysql 8添加: <dependency><groupId>mysql</groupId><artifactId>mysql-connector-java</artifactId><version>8.0.29</version></dependency> mysql 5 添加: <dependency><grou…...

guava工具类常用方法
Guava是Google开发的一个Java开源工具类库,它提供了许多实用的工具类和功能,可以简化Java编程中的常见任务。 引入依赖 <dependency><groupId>com.google.guava</groupId><artifactId>guava</artifactId><version>2…...

CSShas伪类选择器案例附注释
<!DOCTYPE html> <html lang="en"> <head><meta charset...
nodejs+vue中医体质的社区居民健康管理系统elementui
可以实现首页、中医体质量表、健康文章、健康视频、我的等,在我的页面可以对医生、小区单元、医疗药品等功能进行操作。目前主要的健康管理系统是以西医为主,而为了传扬中医文化,提高全民健康意识,解决人民日益增长的美好生活需要…...

Kotlin中reified 关键字
前言 在开始之前,让我们先讨论一下泛型。泛型用于为类、函数或接口提供通用的实现。下面是一个示例泛型方法: fun <T> displayValue(value: T) {println(value) }fun main() {displayValue<String>("Generics")displayValue<…...
之alias)
Linux命令(95)之alias
linux命令之alias 1.alias介绍 linux命令alias是用来将/bin目录下的命令进行别名设置,将一些较长的命令进行简化。 alias命令的作用只局限于该次登入的操作,相当于临时变量。 如果对当前用户永久生效,需修改~/.bashrc文件,使用…...
DHCPsnooping 配置实验(2)
DHCP报文泛洪攻击 限制接收到报文的速率 vlan 视图或者接口视图 dhcp request/ dhcp-rate dhcp snooping check dhcp-request enable dhcp snooping alarm dhcp-request enable dhcp snooping alarm dhcp-request threshold 1 超过则丢弃报文 查看[Huawei]dis dhcp statistic…...

Qt 综合练习小项目--反金币(2/2)
目录 4 选择关卡场景 4.2 背景设置 4.3 创建返回按钮 4.3 返回按钮 4.4 创建选择关卡按钮 4.5 创建翻金币场景 5 翻金币场景 5.1 场景基本设置 5.2 背景设置 5.3 返回按钮 5.4 显示当前关卡 5.5 创建金币背景图片 5.6 创建金币类 5.6.1 创建金币类 MyCoin 5.6.…...
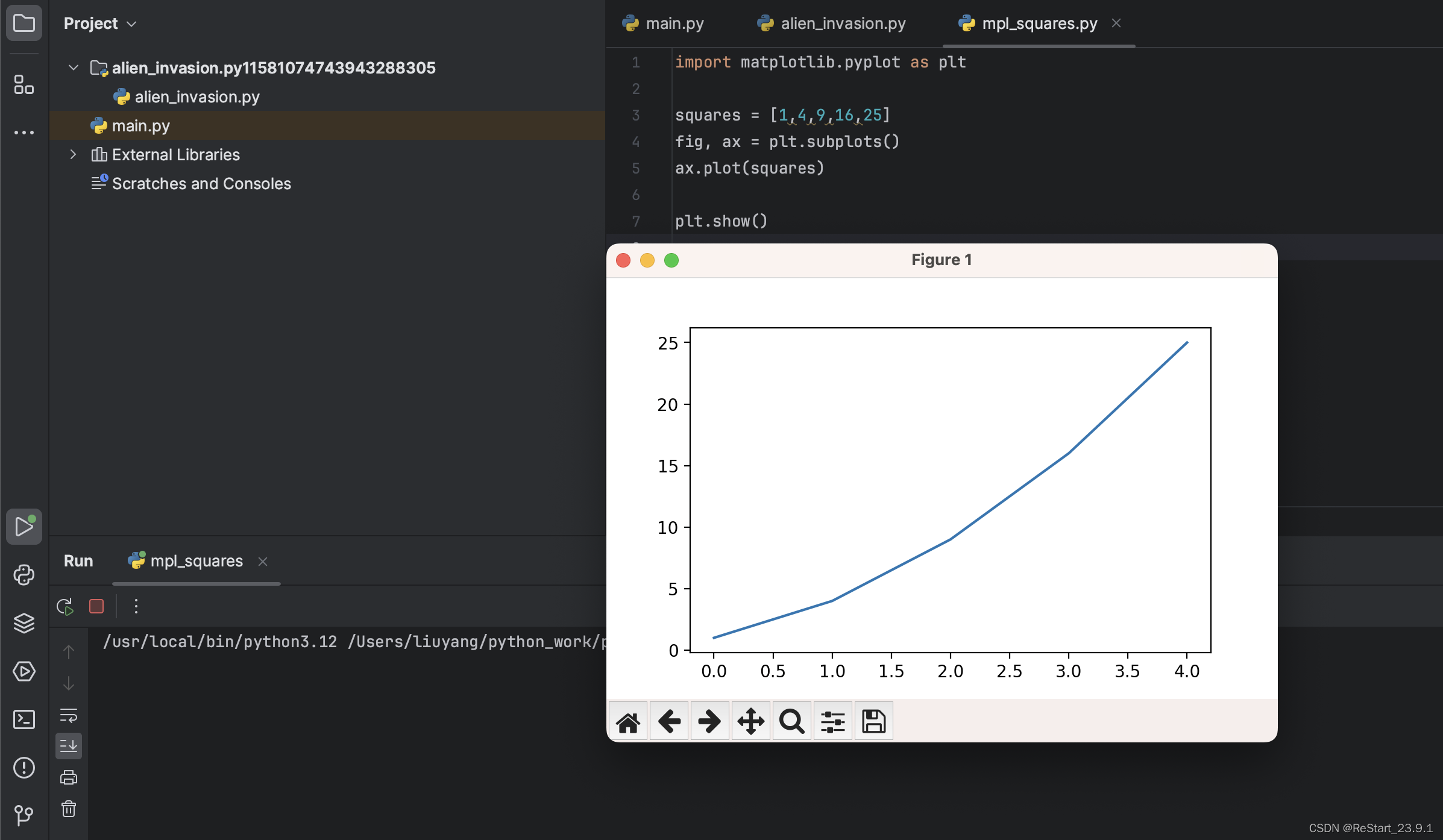
安装matplotlib__pygame,以pycharm调入模块
安装pip 安装matplotlib 安装完毕,终端输入pip list检查 导入模块出现bug,发现不是matplotlib包的问题,pycharm版本貌似不兼容,用python编辑器可正常绘图,pygame也可正常导入。 pycharm版本问题解决 终…...

编写可扩展的软件:架构和设计原则
在今天的软件开发领域,可扩展性是一个至关重要的概念。无论您是开发一个小型应用程序还是一个大规模的软件系统,都需要考虑如何使您的软件能够在不断变化的需求下进行扩展和演进。本文将探讨编写可扩展软件的关键架构和设计原则,以帮助开发人…...
算法-排序算法
0、算法概述 0.1 算法分类 十种常见排序算法可以分为两大类: 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。 非比较类排序:不通过比较来决定元素间…...

Android_Monkey_测试执行策略及标准
一、Monkey命令概述 NO命令说明用法解释1 -p ALLOWED_PACKAGE用于指定某个apk,可以使用多个-p选项,但是每个-p命令选项只能用于一个apk 如果不指定-p,Monkey就会默认进行全系统测试。 -p com.android.contacts可以进行特定apk的Monkey测试2 …...
windows安装nginx
官网提供的下载地址:nginx: download nginx1.25.2下载地址:http://nginx.org/download/nginx-1.25.2.zip 直接运行nginx.exe会闪退,我们还得使用cmd/git bash/power shell 命令进行启动; 个人更喜欢git bash; 运行命…...

Java日期的学习篇
关于日期的学习 目录 关于日期的学习JDK8以前的APIDate Date常用APIDate的API应用 SimpleDateFormatSimpleDateFormat常用API测试 反向格式化(逆操作)测试 训练案例需求(秒杀活动)实现 Calendar需求痛点常见API应用测试 JDK8及以后的API(修改与新增)为啥学习(推荐使用)新增的AP…...

spark on hive
需要提前搭建好hive,并对hive进行配置。 1、将hive的配置文件添加到spark的目录下 cp $HIVE_HOME/conf/hive-site.xml $SPARK_HOME/conf2、开启hive的hivemetastore服务 提前创建好启动日志存放路径 mkdir $HIVE_HOME/logStart nohup /usr/local/lib/apache-hi…...

Linux Vi编辑器基础操作指南
Linux Vi编辑器基础操作指南 Linux中的Vi是一个强大的文本编辑器,虽然它有一些陡峭的学习曲线,但一旦掌握了基本操作,它就变得非常高效。以下是Vi编辑器的一些基本用法: 打开Vi编辑器: vi 文件名退出Vi编辑器ÿ…...
WEB3 创建React前端Dapp环境并整合solidity项目,融合项目结构便捷前端拿取合约 Abi
好 各位 经过我们上文 WEB3 solidity 带着大家编写测试代码 操作订单 创建/取消/填充操作 我们自己写了一个测试订单业务的脚本 没想到运行的还挺好的 那么 今天开始 我们就可以开始操作我们前端 Dapp 的一个操作了 在整个过程中 确实是没有我们后端的操作 或者说 我们自己就…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
