每日一题 279完全平方数(完全背包)
题目
完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
提示:
1 <= n <= 104
题解
记忆化搜索
class Solution {private int[][] cache;public int numSquares(int n) {// if (n == 1) {// return 1;// }int len = (int) Math.sqrt(n);cache = new int[len][n + 1];for (int i = 0; i < len; i++) {Arrays.fill(cache[i],-1);}int ans = dfs(len - 1, n);return ans < Integer.MAX_VALUE / 2 ? ans : -1;}public int dfs(int i, int c) {if (i < 0) {return c == 0 ? 0 : Integer.MAX_VALUE / 2;}if (cache[i][c] != -1) {return cache[i][c];}if (c < (i + 1) * (i + 1)) {return cache[i][c] = dfs(i - 1, c);}return cache[i][c] = Math.min(dfs(i - 1, c), dfs(i, c - (i + 1) * (i + 1)) + 1);}
}
递推
class Solution {public int numSquares(int n) {int len = (int)Math.sqrt(n);int[][] f = new int[2][n + 1];Arrays.fill(f[0], Integer.MAX_VALUE / 2);f[0][0] = 0;for (int i = 0; i < len; i++) {for (int c = 1; c <= n; c++) {if (c < (i + 1) * (i + 1)) {f[(i + 1)%2][c] = f[i%2][c];} else {f[(i + 1)%2][c] = Math.min(f[i%2][c],f[(i + 1)%2][c - (i + 1) * (i + 1)] + 1);}}}int ans = f[len%2][n];return ans < Integer.MAX_VALUE / 2 ? ans : -1;}
}
两个数组优化
class Solution {public int numSquares(int n) {int len = (int)Math.sqrt(n);int[][] f = new int[2][n + 1];Arrays.fill(f[0], Integer.MAX_VALUE / 2);f[0][0] = 0;for (int i = 0; i < len; i++) {for (int c = 1; c <= n; c++) {if (c < (i + 1) * (i + 1)) {f[(i + 1)%2][c] = f[i%2][c];} else {f[(i + 1)%2][c] = Math.min(f[i%2][c],f[(i + 1)%2][c - (i + 1) * (i + 1)] + 1);}}}int ans = f[len%2][n];return ans < Integer.MAX_VALUE / 2 ? ans : -1;}
}
一个数组优化
class Solution {public int numSquares(int n) {int len = (int)Math.sqrt(n);int[] f = new int[n + 1];Arrays.fill(f, Integer.MAX_VALUE / 2);f[0] = 0;for (int i = 0; i < len; i++) {for (int c = (i + 1) * (i + 1); c <= n; c++) {f[c] = Math.min(f[c],f[c - (i + 1) * (i + 1)] + 1);}}int ans = f[n];return ans < Integer.MAX_VALUE / 2 ? ans : -1;}
}
相关文章:
)
每日一题 279完全平方数(完全背包)
题目 完全平方数 给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。 完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而…...
创意中秋与国庆贺卡 - 用代码为节日增添喜悦
目录 编辑 引言 贺卡的初始主题 - 中秋节 点击头像,切换至国庆主题 文本动画 用代码制作这个贺卡 获取完整代码(简单免费) 总结 引言 中秋佳节和国庆日是中国两个重要的传统节日,一个寓意团圆与祝福,另一个…...
专业综合课程设计 - 优阅书城项目(第一版)
此项目是《专业综合课程设计》带练项目 实现的功能有: 登录、注销、添加图书、删除图书、编辑图书 包含资源: 优阅书城(bookstore)源码 数据库数据 课程笔记 下载链接:https://wwpv.lanzoue.com/i79nx1av4doj 登录功…...

【剑指Offer】13.机器人的运动范围
题目 地上有一个 rows 行和 cols 列的方格。坐标从 [0,0] 到 [rows-1,cols-1] 。一个机器人从坐标 [0,0] 的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于 thresh…...
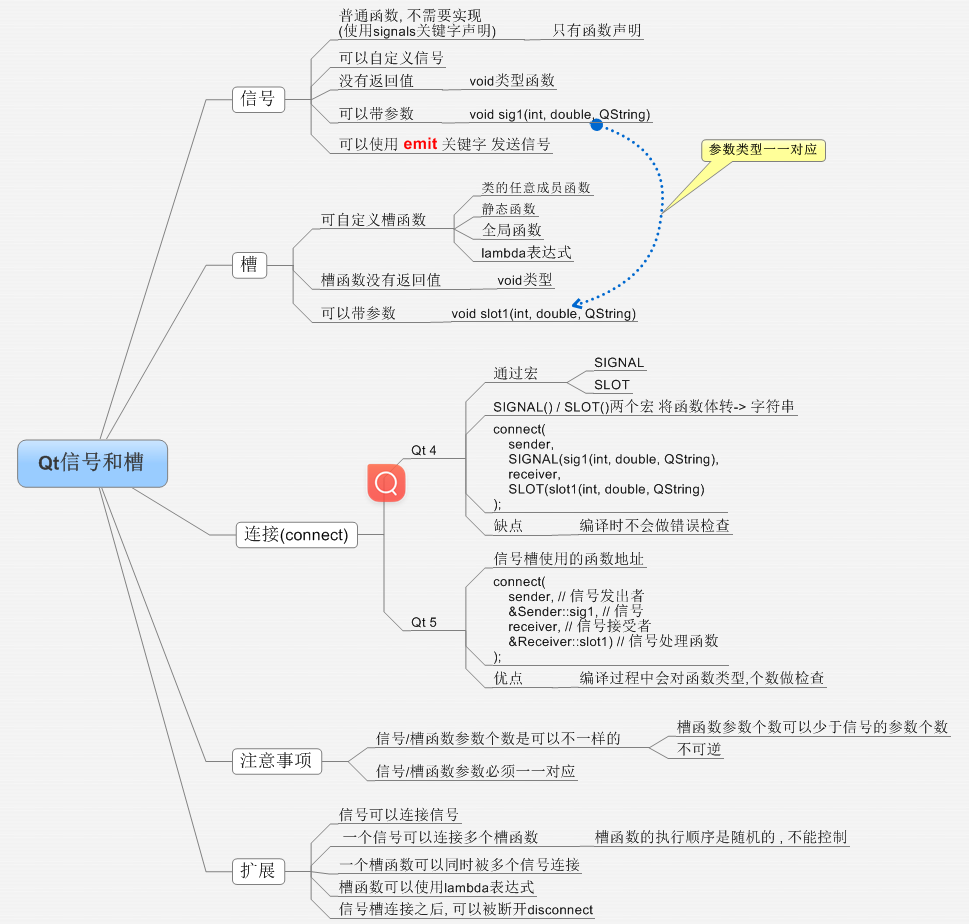
【Qt基础篇】信号和槽
文章目录 一些常见的bug:字符集不对产生的错误VS平台中文乱码 QT的优点关于.pro文件QtCreator快捷键最简单的qt程序按钮的创建对象模型**Qt窗口坐标**体系信号和槽机制connect函数系统自带的信号和槽案例:实现点击按钮-关闭窗口的案例 自定义信号和槽案例…...

.netCore用DispatchProxy实现动态代理
在 .NET Core 中,你可以使用 DispatchProxy 类来实现动态代理。DispatchProxy 允许你在运行时创建一个代理对象,该代理对象可以拦截对其所代理的对象的方法调用,并在方法调用前后执行自定义的逻辑。这在 AOP(面向切面编程…...
好奇喵 | Tor浏览器——访问.onion网址,揭开Dark Web的神秘面纱
前言 在之前的博客中: 1.Surface Web —> Deep Web —> Dark Web,我们解释了表层网络、深层网络等的相关概念; 2.Tor浏览器——层层剥开洋葱,我们阐述了Tor的历史和基本工作原理; 3.Tor浏览器…...
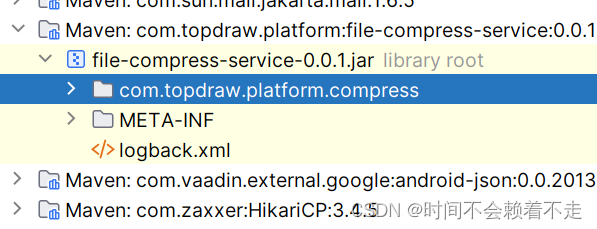
Maven 中引用其他项目jar包出现BOOT-INF问题
问题 在B项目中引入A项目的类,但是发现怎么也引入不进来 A项目打包之后,想在B项目中引用jar 在B项目中发现类文件无法引用 参考网上进行清缓存等一系列操作都没有解决。 最后发现引用的jar包中包含BOOT-INF, 然后去A项目中查找ÿ…...

PHP框架面试题
目录 1、什么是PHP框架? 2、常见的PHP框架有哪些? 3、为什么要使用PHP框架? 4、什么是路由?PHP框架中的路由是如何实现的? 5.TP的特性有哪些? 6.laravel有那些特点? 7.TP框架和Laravel框架的区别 8.tp5和tp6区…...
如何清理C盘
当前最棘手的问题是C盘满了,如何清理成了一个大问题,在本篇文章中我将记录我在清理c盘空间过程中的探索。 2023-10-06探索无果,记录于此。...

计算机网络基础知识
1 计算机网络是指将多台计算机连接在一起,以便它们可以相互通信和共享资源的系统。在本文中,我们将详细介绍计算机网络的基础知识,包括网络的分类、网络协议、网络拓扑、网络设备和网络安全等方面的内容。 网络分类 计算机网络可以根据其范…...
Go语言面经进阶10问
1.Golang可变参数 函数方法的参数,可以是任意多个,这种我们称之为可以变参数,比如我们常用的fmt.Println()这类函数,可以接收一个可变的参数。可以变参数,可以是任意多个。我们自己也可以定义可以变参数,可…...

大厂真题:【DP】米哈游2023秋招-米小游与魔法少女-奇运
题目描述与示例 题目描述 米小游都快保底了还没抽到希儿,好生气哦!只能打会活动再拿点水晶。 米小游和世界第一可爱的魔法少女 TeRiRi 正在打 BOSS,BOSS 的血量为h,当 BOSS 血量小于等于0时,BOSS 死亡。TeRiRi 有一…...
后端面经学习自测(一)
文章目录 1、MySQL-MVCC2、MySQL-原子性怎么实现3、MySQL-持久性怎么实现隔离性怎么实现 4、操作系统-死锁产生手写死锁死锁排查 5、操作系统-避免死锁死锁的四个必要条件预防死锁 6、操作系统-pageCache是什么零拷贝 7、计算机网络-TCP的可靠性和顺序性怎么实现8、计算机网络-…...

win10、win11安装Ubuntu 22.04
目前为止(2023年10月6日),最新的 Ubuntu 版本是 Ubuntu 22.04。你可以按照以下步骤在 Windows 上使用 WSL 安装 Ubuntu 22.04: 检查系统要求: 确保你的操作系统是 Windows 10 或更高版本,并已安装 Windows …...
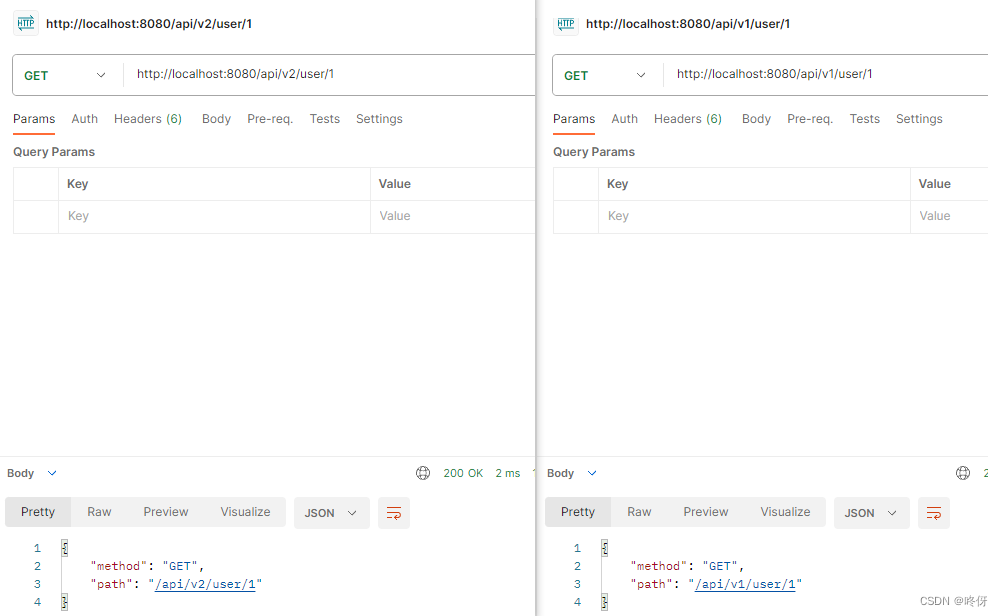
golang gin框架1——简单案例以及api版本控制
gin框架 gin是golang的一个后台WEB框架 简单案例 package mainimport ("github.com/gin-gonic/gin""net/http" )func main() {r : gin.Default()r.GET("/ping", func(c *gin.Context) {//以json形式输出,还可以xml protobufc.JSON…...

Redisson—分布式对象
每个Redisson对象实例都会有一个与之对应的Redis数据实例,可以通过调用getName方法来取得Redis数据实例的名称(key)。 RMap map redisson.getMap("mymap"); map.getName(); // mymap 所有与Redis key相关的操作都归纳在RKeys这…...

alsa pcm接口之在unix环境的传输方法
在unix环境,数据片段响应被接受通过standard I/O call或事件等待路径(poll或select功能),为完成列表,异步通知响应该被列举出来.ALSA实现那些方法被描述在ALSA transfers部分. 标准I/O传输(Standadrd I/O transfers) 这个标准I/O传输常常使用read和write C语言函数集,对于那些函…...
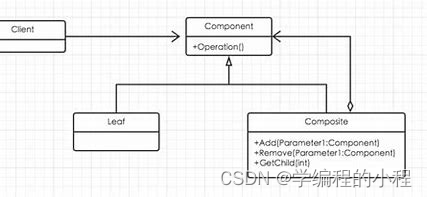
小谈设计模式(20)—组合模式
小谈设计模式(20)—组合模式 专栏介绍专栏地址专栏介绍 组合模式对象类型叶节点组合节点 核心思想应用场景123 结构图结构图分析 Java语言实现首先,我们需要定义一个抽象的组件类 Component,它包含了组合节点和叶节点的公共操作&a…...

sheng的学习笔记-【中文】【吴恩达课后测验】Course 1 - 神经网络和深度学习 - 第三周测验
课程1_第3周_测验题 目录:目录 第一题 1.以下哪一项是正确的? A. 【 】 a [ 2 ] ( 12 ) a^{[2](12)} a[2](12)是第12层,第2个训练数据的激活向量。 B. 【 】X是一个矩阵,其中每个列都是一个训练示例。 C. 【 】 a 4 […...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
