sheng的学习笔记-【中文】【吴恩达课后测验】Course 1 - 神经网络和深度学习 - 第三周测验
课程1_第3周_测验题
目录:目录
第一题
1.以下哪一项是正确的?
A. 【 】 a [ 2 ] ( 12 ) a^{[2](12)} a[2](12)是第12层,第2个训练数据的激活向量。
B. 【 】X是一个矩阵,其中每个列都是一个训练示例。
C. 【 】 a 4 [ 2 ] a^{[2]}_4 a4[2] 是第2层,第4个训练数据的激活输出。
D. 【 】 a 4 [ 2 ] a^{[2]}_4 a4[2] 是第2层,第4个神经元的激活输出。
E. 【 】 a [ 2 ] a^{[2]} a[2] 表示第2层的激活向量。
F. 【 】 a [ 2 ] ( 12 ) a^{[2](12)} a[2](12)是第2层,第12个数据的激活向量。
G. 【 】 X X X是一个矩阵,其中每个行是一个训练数据。
答案:
B.【 √ 】X是一个矩阵,其中每个列都是一个训练示例。
D.【 √ 】 a 4 [ 2 ] a^{[2]}_4 a4[2] 是第2层,第4个神经元的激活输出。
E.【 √ 】 a [ 2 ] a^{[2]} a[2] 表示第2层的激活向量。
F.【 √ 】 a [ 2 ] ( 12 ) a^{[2](12)} a[2](12)是第2层,第12个数据的激活向量。
第二题
2.对于隐藏单元,tanh激活通常比sigmoid激活函数更有效,因为其输出的平均值接近于零,因此它可以更好地将数据集中到下一层。
A. 【 】对
B. 【 】不对
答案:
A.【 √ 】对
note:正如tanh所看到的,tanh的输出在-1和1之间,因此它将数据集中在一起,使得下一层的学习变得更加简单。
第三题
3.以下哪一个是层的正向传播的正确矢量化实现,其中 1 ≤ l ≤ L 1 \le l \le L 1≤l≤L
A. 【 】
Z [ l ] = W [ l ] A [ l ] + b [ l ] Z^{[l]}=W^{[l]}A^{[l]}+b^{[l]} Z[l]=W[l]A[l]+b[l]
A [ l + 1 ] = g [ l ] ( Z [ l ] ) A^{[l+1]}=g^{[l]}(Z^{[l]}) A[l+1]=g[l](Z[l])
B. 【 】
Z [ l ] = W [ l ] A [ l ] + b [ l ] Z^{[l]}=W^{[l]}A^{[l]}+b^{[l]} Z[l]=W[l]A[l]+b[l]
A [ l + 1 ] = g [ l + 1 ] ( Z [ l ] ) A^{[l+1]}=g^{[l+1]}(Z^{[l]}) A[l+1]=g[l+1](Z[l])
C. 【 】
Z [ l ] = W [ l − 1 ] A [ l ] + b [ l ] Z^{[l]}=W^{[l-1]}A^{[l]}+b^{[l]} Z[l]=W[l−1]A[l]+b[l]
A [ l ] = g [ l ] ( Z [ l ] ) A^{[l]}=g^{[l]}(Z^{[l]}) A[l]=g[l](Z[l])
D. 【 】
Z [ l ] = W [ l ] A [ l − 1 ] + b [ l ] Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]} Z[l]=W[l]A[l−1]+b[l]
A [ l ] = g [ l ] ( Z [ l ] ) A^{[l]}=g^{[l]}(Z^{[l]}) A[l]=g[l](Z[l])
答案:
D.【 √ 】
Z [ l ] = W [ l ] A [ l − 1 ] + b [ l ] Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]} Z[l]=W[l]A[l−1]+b[l]
A [ l ] = g [ l ] ( Z [ l ] ) A^{[l]}=g^{[l]}(Z^{[l]}) A[l]=g[l](Z[l])
第四题
4.您正在构建一个用于识别黄瓜(y=1)与西瓜(y=0)的二进制分类器。对于输出层,您建议使用哪一个激活函数?
A. 【 】ReLU
B. 【 】Leaky ReLU
C. 【 】sigmoid
D. 【 】tanh
答案:
C.【 √ 】sigmoid
note:
- 来自sigmoid函数的输出值可以很容易地理解为概率。
- Sigmoid输出的值介于0和1之间,这使其成为二元分类的一个非常好的选择。 如果输出小于0.5,则可以将其归类为0,如果输出大于0.5,则归类为1。 它也可以用tanh来完成,但是它不太方便,因为输出在-1和1之间。
第五题
5.考虑以下代码:
A = np.random.randn(4,3)
B = np.sum(A, axis = 1, keepdims = True)
B.shape是多少?
A. 【 】(4,)
B. 【 】(1, 3)
C. 【 】(, 3)
D. 【 】(4, 1)
答案:
D.【 √ 】shape = (4, 1)
note:我们使用(keepdims = True)来确保A.shape是(4,1)而不是(4,),它使我们的代码更加严格。
第六题
6.假设你已经建立了一个神经网络。您决定将权重和偏差初始化为零。以下哪项陈述是正确的?(选出所有正确项)
A. 【 】第一隐藏层中的每个神经元将执行相同的计算。因此,即使在梯度下降的多次迭代之后,层中的每个神经元将执行与其他神经元相同的计算。
B. 【 】第一隐层中的每个神经元在第一次迭代中执行相同的计算。但是在梯度下降的一次迭代之后,他们将学会计算不同的东西,因为我们已经“破坏了对称性”。
C. 【 】第一个隐藏层中的每个神经元将执行相同的计算,但不同层中的神经元执行不同的计算,因此我们完成了课堂上所描述的“对称性破坏”。
D. 【 】即使在第一次迭代中,第一个隐藏层的神经元也会执行不同的计算,因此,它们的参数会以自己的方式不断演化。
答案:
A.【 √ 】第一个隐藏层中的每个神经元节点将执行相同的计算。 所以即使经过多次梯度下降迭代后,层中的每个神经元节点都会计算出与其他神经元节点相同的东西。
第七题
7.逻辑回归的权重w应该随机初始化,而不是全部初始化为全部零,否则,逻辑回归将无法学习有用的决策边界,因为它将无法“打破对称”。
A. 【 】对
B. 【 】不对
答案:
B.【 √ 】不对
note:
Logistic回归没有隐藏层。 如果将权重初始化为零,则Logistic回归中的第一个示例x将输出零,但Logistic回归的导数取决于不是零的输入x(因为没有隐藏层)。 因此,在第二次迭代中,如果x不是常量向量,则权值遵循x的分布并且彼此不同。
第八题
8.你已经为所有隐藏的单位建立了一个使用tanh激活的网络。使用np.random.randn(…, …) * 1000将权重初始化为相对较大的值。会发生什么?
A. 【 】没关系。只要随机初始化权重,梯度下降不受权重大小的影响。
B. 【 】这将导致tanh的输入也非常大,从而导致梯度也变大。因此,你必须将设置得非常小,以防止发散;这将减慢学习速度。
C. 【 】这将导致tanh的输入也非常大,导致单元被“高度激活”。与权重从小值开始相比,加快了学习速度。
D. 【 】这将导致tanh的输入也非常大,从而导致梯度接近于零。因此,优化算法将变得缓慢。
答案:
D.【 √ 】这将导致tanh的输入也很大,因此导致梯度接近于零, 优化算法将因此变得缓慢。
note:tanh对于较大的值变得平坦,这导致其梯度接近于零。 这减慢了优化算法。
第九题
9.考虑以下1个隐层的神经网络:

A. 【 】 W [ 1 ] W^{[1]} W[1]的形状是(2, 4)
B. 【 】 b [ 1 ] b^{[1]} b[1]的形状是(4, 1)
C. 【 】 W [ 1 ] W^{[1]} W[1]的形状是(4, 2)
D. 【 】 b [ 1 ] b^{[1]} b[1]的形状是(2, 1)
E. 【 】 W [ 2 ] W^{[2]} W[2]的形状是(1, 4)
F. 【 】 b [ 2 ] b^{[2]} b[2]的形状是(4, 1)
G. 【 】 W [ 2 ] W^{[2]} W[2]的形状是(4, 1)
H. 【 】 b [ 2 ] b^{[2]} b[2]的形状是(1, 1)
答案:
B.【 √ 】 b [ 1 ] b^{[1]} b[1]的形状是(4, 1)
C.【 √ 】 W [ 1 ] W^{[1]} W[1]的形状是(4, 2)
E.【 √ 】 W [ 2 ] W^{[2]} W[2]的形状是(1, 4)
H.【 √ 】 b [ 2 ] b^{[2]} b[2]的形状是(1, 1)
第十题
10.在和上一问相同的网络中, Z [ 1 ] Z^{[1]} Z[1]和 A [ 1 ] A^{[1]} A[1]的维度是多少?
A. 【 】 Z [ 1 ] Z^{[1]} Z[1]和 A [ 1 ] A^{[1]} A[1]是(4,1)
B. 【 】 Z [ 1 ] Z^{[1]} Z[1]和 A [ 1 ] A^{[1]} A[1]是(1,4)
C. 【 】 Z [ 1 ] Z^{[1]} Z[1]和 A [ 1 ] A^{[1]} A[1]是(4,m)
D. 【 】 Z [ 1 ] Z^{[1]} Z[1]和 A [ 1 ] A^{[1]} A[1]是(4,2)
答案:
C.【 √ 】 Z [ 1 ] Z^{[1]} Z[1]和 A [ 1 ] A^{[1]} A[1]是(4,m)
相关文章:

sheng的学习笔记-【中文】【吴恩达课后测验】Course 1 - 神经网络和深度学习 - 第三周测验
课程1_第3周_测验题 目录:目录 第一题 1.以下哪一项是正确的? A. 【 】 a [ 2 ] ( 12 ) a^{[2](12)} a[2](12)是第12层,第2个训练数据的激活向量。 B. 【 】X是一个矩阵,其中每个列都是一个训练示例。 C. 【 】 a 4 […...
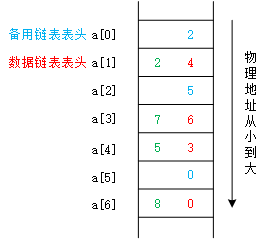
一文详解动态链表和静态链表的区别
1、引言 本文主要是对动态链表和静态链表的区别进行原理上的讲解分析,先通过对顺序表和动态链表概念和特点的原理性介绍,进而引申出静态链表的作用,以及其概念。通过这些原理性的概述,最后总结归纳出动态链表和静态链表的区别。本…...
[C国演义] 第十三章
第十三章 三数之和四数之和 三数之和 力扣链接 根据题目要求: 返回的数对应的下标各不相同三个数之和等于0不可包含重复的三元组 – – 即顺序是不做要求的 如: [-1 0 1] 和 [0, 1, -1] 是同一个三元组输出答案顺序不做要求 暴力解法: 排序 3个for循环 去重 — — N^3, …...
<二>Qt斗地主游戏开发:过场动画的实现
1. 过场动画效果 2. 思路分析 过场动画较为简单,只有一个进度条在进行滚动,因此实现起来不需要动画相关处理,仅需要图片和定时器设定,让进度条动起来即可。我们可以创建一个对话框,设定背景图片以及对话框透明无边框&a…...
)
链式法则(Chain Rule)
定义 链式法则(Chain Rule)是概率论和统计学中的一个基本原理,用于计算联合概率分布或条件概率分布的乘积。它可以用于分解一个复杂的概率分布为多个较简单的条件概率分布的乘积,从而简化概率分析问题。 链式法则有两种常见的形…...

AUTOSAR COM模块框架梳理
框架: COM的功能主要就是两个: 把IPDU内的signal提取出来提供给SWC使用,把SWC发送的signal拷贝到IPDU buffer内 所以,COM的关键字是 signal, signal group, IPDU, IPDU group Signal group 是为了保证 Complex Data Types 的数…...

详细介绍区块链之挖矿
对不起,大家,这篇文章对作者来说实在是太有意义和含金量了,作者想把它设置为关注博主才能见全文,请大家理解!如果觉得还是看不懂,抱歉耽误大家的时间,就请取消关注!!&…...
)
华为OD机试真题-路灯照明问题(Java/C++/Go/Python)
【华为OD机试真题】路灯照明问题(Java/C++/Go/Python) 题目描述 在一条笔直的公路上安装了N个路灯,从位置0开始安装,路灯之间间距固定为100米。 每个路灯都有自己的照明半径,请计算第一个路灯和最后一个路灯之间,无法照明的区间的长度和。 输入描述 第一行为一个数N…...

嵌入式技术面试基本规则
潜规则1:面试的本质不是考试,而是告诉面试官你会做什么 经验不够的小伙伴特别容易犯的一个错误,不清楚面试官到底想问什么,其实整个面试中面试官并没有想难倒你的意思,只是想通过提问的方式来知道你会什么。 比如stm…...
osg实现自定义插件读取自定义格式的模型文件到场景
目录 1. 前言 2. 预备知识 3. 工具、原料 4. 代码实现 1. 前言 osg提供了很多插件来读取模型文件到场景中,这些插件支持大约70种格式类型的文件,但现实中的文件是各式各样,osg不可能囊括所有类型文件,当osg不支持某种类型格式…...

redis进阶
redis.conf 启动的时候就通过配置文件来启动的! # 这个不是配置的,就是在这儿说明一下 # 当配置中需要配置内存大小时,可以使用 1k, 5GB, 4M 等类似的格式,其转换方式如下(不区分大小写) # # 1k > 1000 bytes # 1kb > 102…...
(一)正点原子STM32MP135移植——准备
一、简述 使用板卡:正点原子的ATK-DLMP135 V1.2 从i.mx6ull学习完过来,想继续学习一下移植uboot和内核的,但是原子官方没有MP135的移植教程,STM32MP157的移植教程用的又是老版本的代码,ST官方更新后的代码不兼容老版本…...

Kotlin的关键字 lateinit 和 lazy
序、完善一下曾经的草稿。 Kotlin通常要求我们在定义属性后立即对起进行初始化,当我们不知道理想的初始值时,这样做似乎很奇怪,尤其是在生命周期驱动android属性的情况下。 lateinit 简介 lateinit,Kotlin提供的一个可以延迟初…...
阿里云服务器ECS详细介绍_云主机_服务器托管_弹性计算
阿里云服务器ECS英文全程Elastic Compute Service,云服务器ECS是一种安全可靠、弹性可伸缩的云计算服务,阿里云提供多种云服务器ECS实例规格,如经济型e实例、通用算力型u1、ECS计算型c7、通用型g7、GPU实例等,阿里云服务器网分享阿…...

12、建立健全人员培训体系
9、大小屏分离与精细化审核 10、质量审核的设立与合并 11、视频分类建议 内容仓为公司其他部门输送了许多人才,既包括有潜力的主管,也有表现突出或者具备某些特殊能力的员工,从内容仓走出的同事,有些已经成为公司重要业务某个方…...
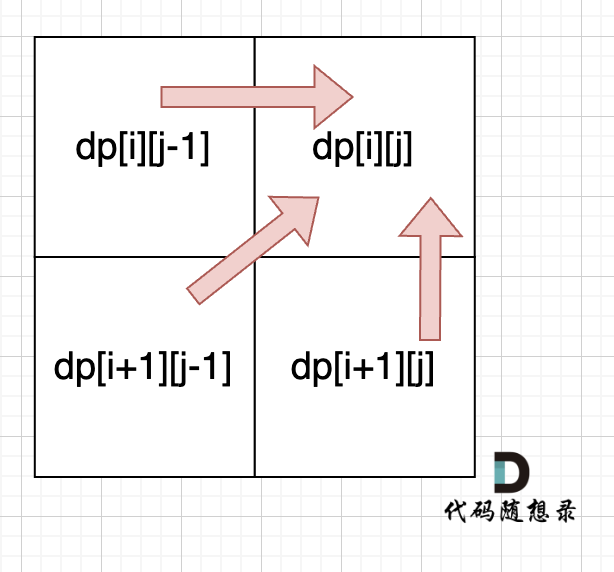
代码随想录算法训练营第五十九天 | 647. 回文子串 516.最长回文子序列
1. 回文子串 647. 回文子串 - 力扣(LeetCode) 一个子串左右两个元素相等,并且中间对称,才是回文子串 即 ij 时,[i1: j-1]对称 dp[i][j]: [i:j] 是否是回文字串 当 子串长度大于2 由 dp[i1][j-1] 推出…...

React Redux
redux是什么 Redux是一个模式和库,用于管理和更新应用程序状态,使用称为“action”的事件。它是需要在整个应用程序中使用的状态的集中存储,规则确保状态只能以可预测的方式更新。 Redux主要有三个功能: 获取当前状态更新状态监…...

StreamingLLM - 处理无限长度的输入
文章目录 关于 StreamingLLM使用关于 StreamingLLM Efficient Streaming Language Models with Attention Sinks GitHub : https://github.com/mit-han-lab/streaming-llm论文:https://arxiv.org/abs/2309.17453在流媒体应用程序(如多轮对话)中 部署大型语言模型(LLM)是迫…...

[Linux 命令] nm 详解
1. nm 命令: 显示关于指定 File 中符号的信息,文件可以是对象文件、可执行文件或对象文件库。如果文件没有包含符号信息,nm 命令报告该情况,但不把它解释为出错条件。 nm 命令缺省情况下报告十进制符号表示法下的数字值。 2. 命…...

好文学作品的鉴赏标准
好文学作品的鉴赏标准 2023年诺贝尔文学奖颁给了挪威剧作家约恩福瑟。由于之前的博彩公司给中国作家残雪开出了最高的赔率,以及诺贝尔官方推特在揭晓奖项前发布了一张泰戈尔99年前访华的老照片,残雪的获奖氛围在国内各类媒体的渲染下被拉至极高。当奖项…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
