数字IC前端学习笔记:数字乘法器的优化设计(进位保留乘法器)
相关阅读
数字IC前端![]() https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482
https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482
阵列乘法器设计中限制乘法器速度的是随着数据位宽而迅速增大的串行进位链,如果使用进位保留加法器,则可以避免在设计中引入较长时间的等待,即可以将两、三个数相加时不同比特位的加法割裂开,使进位得到保留而不是立刻将进位传递给更高位运算,进位保留加法器的结构如图1所示。
 图1 进位保留乘法器
图1 进位保留乘法器
其实进位保留加法器和普通全加器的内部结构一模一样,但不同的是对于进位的处理,普通的全加器接受两位加数和一位进位,输出一位和以及一位进位。而保留进位加法器接受三位加数的输入,输出两位,具体的转换如图2所示。
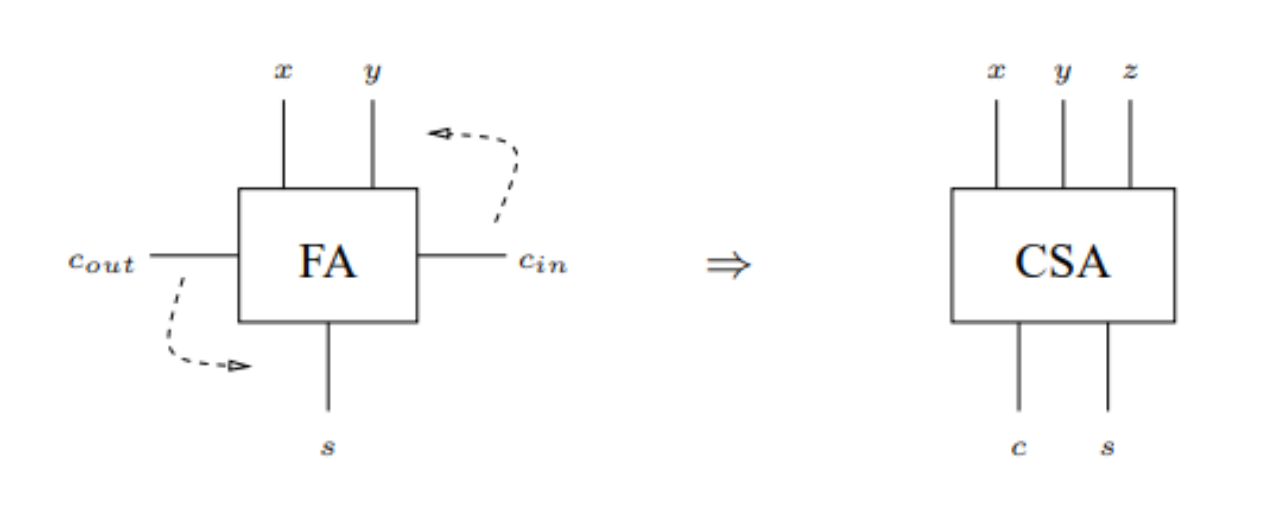 图2 全加器和保留进位加法器的转换
图2 全加器和保留进位加法器的转换
使用保留进位加法器组成多位加法器时,本文采用了与传统串行进位加法器不同的设计方案,不是将多个全加器首尾相连方式串行传播进位信号,而是多个保留进位加法器并行输出,因为这种保留进位加法器输入三位,输出两位,所以也把它叫做3-2压缩器(3-2 compressor)。
进位保留乘法器的结构图如图3所示,可以看到,与之前的阵列乘法器相比,进位保留乘法器对于输出的进位,并不将其传递给本级的高位加法器,而是传递给下一级的高位乘法器,在最后一级使用一个被称为向量合并加法器(图中用绿色框出)的模块来处理最后的两个多位二进制数。向量合并加法器可以选择普通的串行进位加法器或者超前进位加法器,还可以是其他高效的加法器。四位进位保留加法器的资源规划如表1所示。
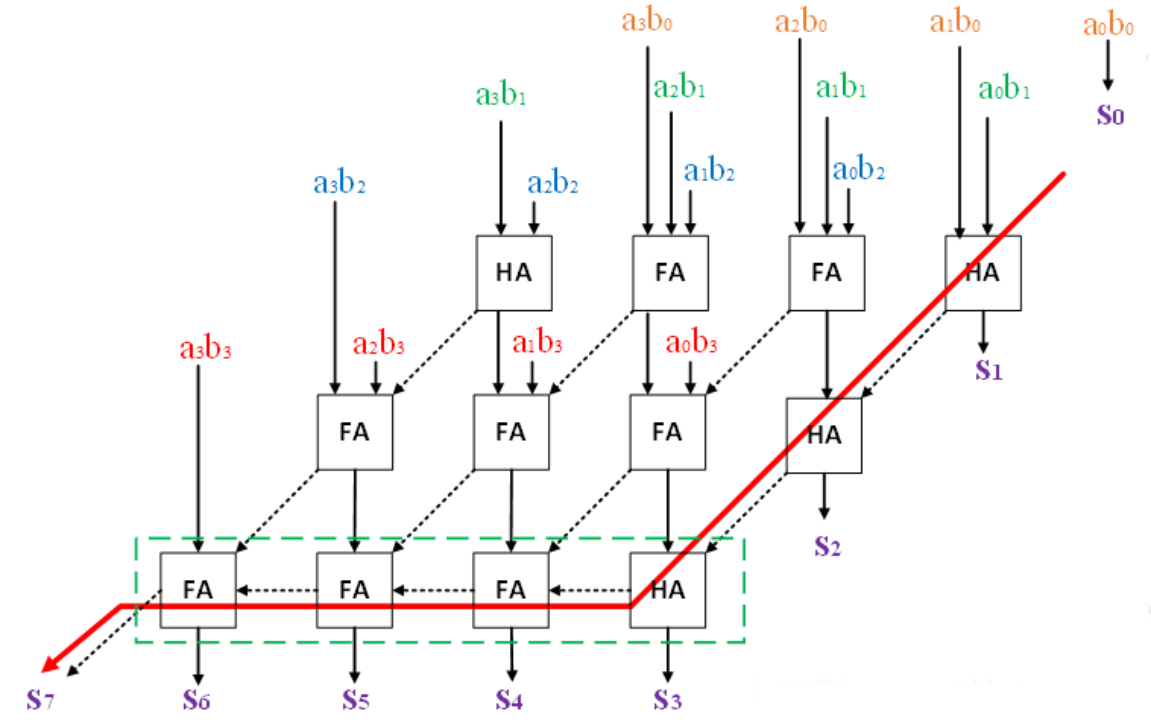 图3 进位保留乘法器结构
图3 进位保留乘法器结构
表4-1 无符号4位二进制乘法规划
| A3 B3 | A2 B2 | A1 B1 | A0 B0 | 被乘数 乘数 | 资源配置 | ||||
| A3B1 | A3B0 A2B1 | A2B0 A1B1 | A1B0 A0B1 | A0B0 | 部分积0 部分积1 上级进位 | 第1行加法器 | |||
| C13 A3B2 | S13 A2B2 C12 | S12 A1B2 C11 | S11 A0B2 C10 | S10 | S00 | 第1行和 部分积2 上级进位 | 第2行乘法器 | ||
| C23 A3B3 | S23 A2B3 C22 | S22 A1B3 C21 | S21 A0B3 C20 | S20 | 第2行和 部分积3 上级进位 | 第3行乘法器 | |||
| C33 | S33 | S32 | S31 | S30 | 第3行和 | 向量合并加法器 | |||
| C32 | C31 | C30 | 第3行和 |
具体的Verilog代码实现见附录,Modelsim软件仿真截图如图4所示。使用Synopsis的综合工具Design Compiler综合的结果如图5所示,综合使用了0.13μm工艺库。
 图4 进位保留乘法器仿真结果
图4 进位保留乘法器仿真结果
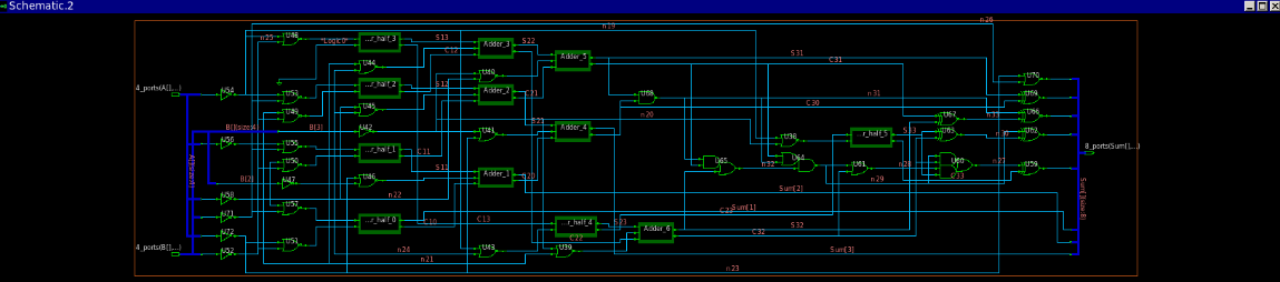 图5 进位保留乘法器综合结果
图5 进位保留乘法器综合结果
在Design Compiler中使用report_timing命令,可以得到关键路径的延迟,如图6所示。使用report_area命令,报告所设计电路的面积占用情况,如图7所示。
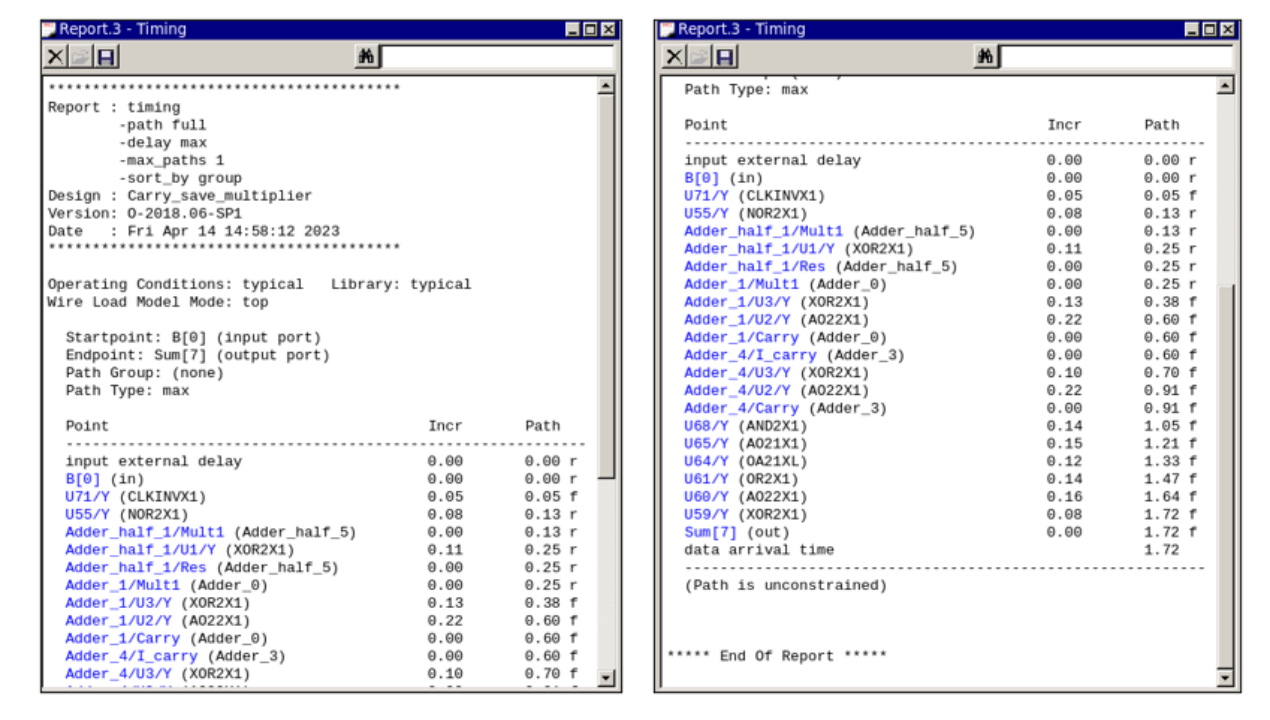 图6 关键路径报告
图6 关键路径报告
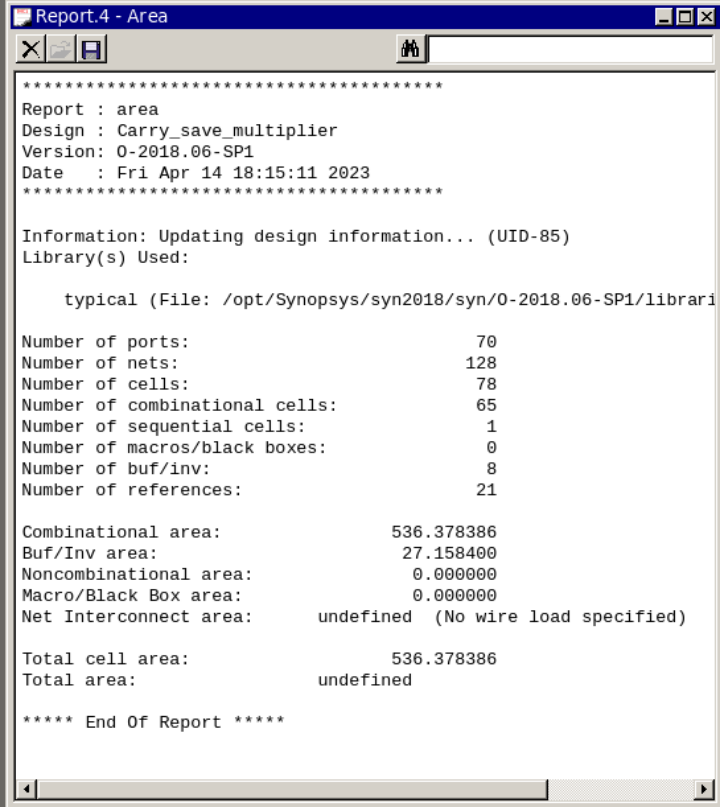
图7 面积报告
进位保留乘法器的Verilog代码如下所示。
module Carry_save_multiplier(input [3:0]A,B,output[7:0]Sum);wire [3:0]partial_product[3:0];//产生部分积assign partial_product[0]=B[0]?A:0;assign partial_product[1]=B[1]?A:0;assign partial_product[2]=B[2]?A:0;assign partial_product[3]=B[3]?A:0;//中间进位wire C10,C11,C12,C13;wire C20,C21,C22,C23;wire C30,C31,C32,C33;//中间和wire S11,S12,S13;wire S21,S22,S23;wire S31,S32,S33;//第一行加法器assign Sum[0]=partial_product[0][0];Adder_half Adder_half_0(partial_product[0][1],partial_product[1] [0],Sum[1],C10);Adder_half Adder_half_1(partial_product[0][2],partial_product[1][1],S11,C11);Adder_half Adder_half_2(partial_product[0][3],partial_product[1][2],S12,C12);Adder_half Adder_half_3(partial_product[1][3],1'b0,S13,C13);//第二行乘法器Adder Adder_1(S11,partial_product[2][0],C10,Sum[2],C20);Adder Adder_2(S12,partial_product[2][1],C11,S21,C21);Adder Adder_3(S13,partial_product[2][2],C12,S22,C22);Adder_half Adder_half_4(C13,partial_product[2][3],S23,C23);//第三行加法器Adder Adder_4(S21,partial_product[3][0],C20,Sum[3],C30);Adder Adder_5(S22,partial_product[3][1],C21,S31,C31);Adder Adder_6(S23,partial_product[3][2],C22,S32,C32);Adder_half Adder_half_5(C23,partial_product[3][3],S33,C33);//向量合并加法器assign Sum[7:4]={C33,S33,S32,S31}+{1'b0,C32,C31,C30};endmodulemodule Adder (input Mult1,input Mult2,input I_carry,output Res,output Carry
);assign Res = Mult1 ^ Mult2 ^ I_carry;assign Carry = (Mult1 & Mult2) | ((Mult1 ^ Mult2) & I_carry);endmodulemodule Adder_half (input Mult1,input Mult2,output Res,output Carry
);assign Res = Mult1 ^ Mult2;assign Carry = Mult1 & Mult2;
endmodule相关文章:

数字IC前端学习笔记:数字乘法器的优化设计(进位保留乘法器)
相关阅读 数字IC前端https://blog.csdn.net/weixin_45791458/category_12173698.html?spm1001.2014.3001.5482 阵列乘法器设计中限制乘法器速度的是随着数据位宽而迅速增大的串行进位链,如果使用进位保留加法器,则可以避免在设计中引入较长时间的等待&…...

prority_queue的学习
优先级队列(Priority Queue)是一种抽象数据类型,它类似于普通的队列或堆栈,但每个元素都有一个关联的优先级,这个优先级决定了元素在队列中的位置和被访问的顺序。在优先级队列中,具有最高优先级的元素通常…...
【vue3】toRef与toRefs的使用,toRef与ref的区别
假期第四篇,对于基础的知识点,我感觉自己还是很薄弱的。 趁着假期,再去复习一遍 1、toRef与toRefs 创建一个ref对象,其value值指向另一个对象中的某个属性 语法:const name toRef(person,‘name’…...

信息论基础第二章部分习题
2.5 证明若H(Y|X)0,则Y是X的函数 若 H ( Y ∣ X ) 0 H(Y|X) 0 H(Y∣X)0,意味着在已知 X X X 的条件下, Y Y Y 的不确定性为零,即给定 X X X 的值,我们完全确定了 Y Y Y 的值。这表明 Y Y Y 的取值完全由 X X…...

信息化发展73
数字经济 数字经济是继农业经济、工业经济之后的更高级经济形态。从本质上看,数字经济是一种新的技术经济范式,它建立在信息与通信技术的重大突破的基础上,以数字技术与实体经济融合驱动的产业梯次转型和经济创新发展的主引擎,在…...

560. 和为 K 的子数组
题目描述 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。 示例 1: 输入:nums [1,1,1], k 2 输出:2示例 2: 输入:nums [1,2,3], k 3 输出:2…...
24 mysql all 查询
前言 这里主要是 探究一下 explain $sql 中各个 type 诸如 const, ref, range, index, all 的查询的影响, 以及一个初步的效率的判断 这里会调试源码来看一下 各个类型的查询 需要 lookUp 的记录 以及 相关的差异 此系列文章建议从 mysql const 查询 开始看 测试表结构…...

【Excel单元格数值统计】python实现-附ChatGPT解析
1.题目 Excel单元格数值统计 知识点: 递归、循环数组 时间限制:2s 空间限制:256MB 限定语言:不限 题目描述: Excel工作表中对选定区域的数值进行统计的功能非常实用。仿照Excel的这个功能,请对给定表格中选中区域中的单元格进行求和统计,并输出统计结果。 为简化计算,假设当…...

爬虫项目实战——爬取B站视频
目标:对B站视频详情页url进行视频的爬取。 注:由于B站的音频和视频的链接是分开的,所以在提取是需要分别提取,然后进行合成。 这里只管提取,合成的工作以后再说。 具体步骤 发送请求 对于视频详情页url地址发送请求 …...
关掉在vscode使用copilot时的提示音
1. 按照图示的操作File --> Preferences --> Settings 2. 搜索框输入关键字Sound,因为是要关掉声音,所以找有关声音的设置 3. 找到如下图所示的选项 Audio Cues:Line Has Inline Suggetion,将其设置为Off 这样,就可以关掉suggest code时…...

【有限域除法】二元多项式除法电路原理及C语言实现
二元多项式除法电路原理 例: g ( x ) = x 4 + x 2 + x + 1 g(x)=x^4 + x^2+x+1...
RabbitMQ核心总结
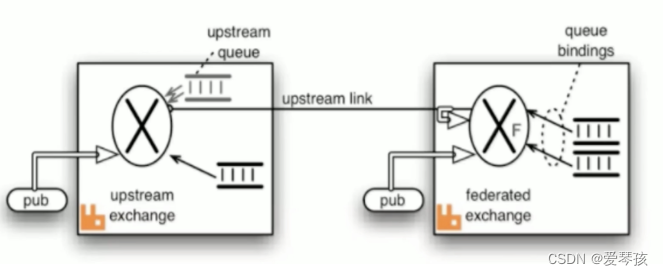
AMQP协议核心概念 RabbitMQ是基于AMQP协议的,通过使用通用协议就可以做到在不同语言之间传递。 server:又称broker,接受客户端连接,实现AMQP实体服务。 connection:连接和具体broker网络连接。 channel:…...
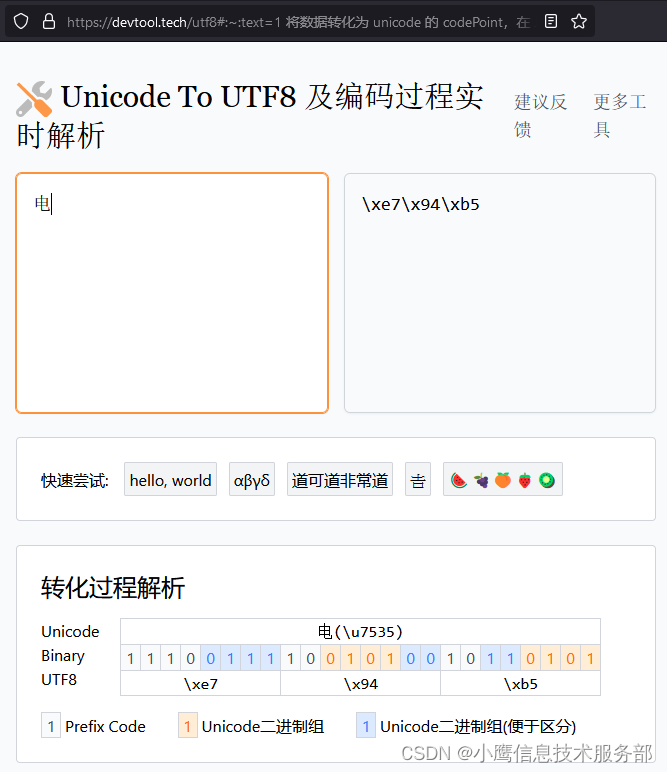
Unicode与UTF-8
软件开发中乱码问题经常遇到,Unicode,UTF-8, ASCII等都是高频词语,不过具体是啥意思其实都不清楚。这个周末研究了一下,略有了解,记录一下。 Unicode Unicode本身是纯理论的东西,和具体计算机实现无关。它…...

A : DS单链表--类实现
Description 用C语言和类实现单链表,含头结点 属性包括:data数据域、next指针域 操作包括:插入、删除、查找 注意:单链表不是数组,所以位置从1开始对应首结点,头结点不放数据 类定义参考 #include<…...

React Hooks —— ref hooks
什么是Hooks Hooks从语法上来说是一些函数。这些函数可以用于在函数组件中引入状态管理和生命周期方法。 React Hooks的优点 简洁 从语法上来说,写的代码少了上手非常简单 基于函数式编程理念,只需要掌握一些JavaScript基础知识与生命周期相关的知识不…...

泛型与Gson解析
/*** 回调接口的一种实现* 用于把网络返回的json字符串转换成参数化类型* 泛型 T 就是用户输入的javaBean的类型*/ public abstract class HttpCallback<T> implements ICallback {Overridepublic void onSuccess (String result) {// result就是网络回来的数据// 把这个…...

c++使用ifstream和ofstream报错:不允许使用不完整的类型
学习《C Primer》关于IO库的部分,输入284页的的代码,出现了报错: 不允许使用不完整的类型 原来的代码: #include <iostream> #include <vector> using namespace std;int main(int argc, char **argv) {ifstream in…...
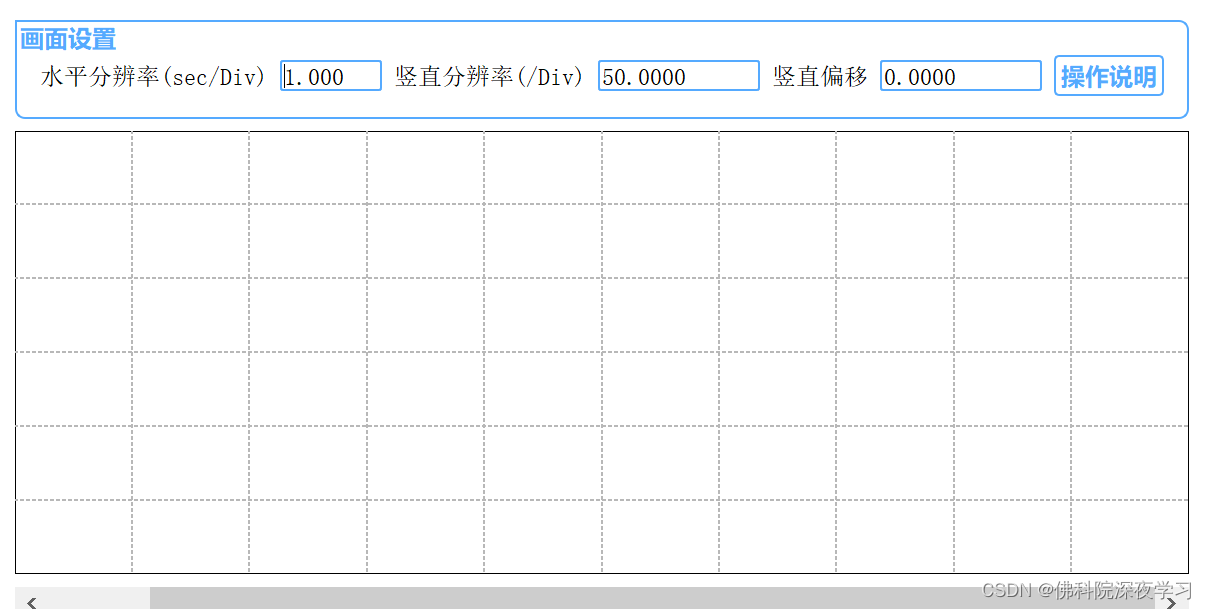
调试器通用波形显示工具
前言:事情起因是我们实验室买了个无线调试器是CMSIS-DAP的,无法使用J-SCOPE显示波形来方便调PID,所以我就在网上找到了个开源工具链接:http://t.csdnimg.cn/ZqZPY使用方法:工具是好工具,就是没有使用手册&a…...

Linux中getopt函数、optind等变量使用详解
getopt函数、optind等变量使用详解 最近在学习《Unix网络编程》vol2时,发现书中例子经常使用一个命令行解析getopt函数,因为函数声明比较特别,根据自己摸索,遂总结出使用方法。 1. getopt函数的声明 该函数是由Unix标准库提供的…...

RDP协议流程详解(二)Basic Settings Exchange 阶段
RDP连接建立过程,在Connection Initiation后,RDP客户端和服务端将进行双方基础配置信息交换,也就是basic settings exchange阶段。在此阶段,将包含两条消息Client MCS Connect Initial PDU和Server MCS Connect Response PDU&…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
