背包问题学习笔记-多重背包问题
题意描述:
有 N 种物品和一个容量是 V 的背包。第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。输入格式
第一行两个整数,N,V (0<N≤1000, 0<V≤20000),用空格隔开,分别表示物品种数和背包容积。接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,分别表示第 i 种物品的体积、价值和数量。输出格式
输出一个整数,表示最大价值。
多重背包的问题根据数据范围的大小划分为了三个难度层次,分别对应三种解法。对应的数据范围分别是:
暴力求解
0<N,V≤100
0<vi,wi,si≤100
二进制优化
0<N≤1000
0<V≤2000
0<vi,wi,si≤2000
单调队列优化
0<N≤1000
0<V≤20000
0<vi,wi,si≤20000
示例:
4 5
1 2 3
2 4 1
3 4 3
4 5 2
10
解题思路:
Alice: 这是一道题拆成了三道题 ?这题这么难
Bob: 丰俭由人,😁
Alice: 多重背包和 01 背包的区别就是每类物品有了数量的限制,01 背包是只能选或者不选,完全背包是由无数种可以选,01 背包是有 k 种可以选。
Bob: 是的,那直接改一下状态转移公式得了,直接按照完全背包的方式换一下最内层的状态转移好了,dp[j] = max(dp[j], dp[j-vi * k] + wi * k) k 取值 0,1,2,3 …
Alice: 为啥要按照完全背包,从最大体积开始求解 ?
Bob: 看状态转移方程,我们还用一维度的 dp 数组的话,对于第 i 个物品,还需要用到第 i-1 个物品的 j-vi * k 的状态,从最大体积往小了计算才是对的。
Alice: 这个理解起来还不太难。
Bob: 是的,这里可以关注一下计算量,暴力去算实际上是 O^3 的,数据范围都是 100,最大也就是 10^6,这样不会超时的。
Alice: 二进制优化讲的是啥 ?
Bob: 二进制优化的前提是,把多重背包转换成 01 背包问题,但是转换的方式有很多种,二进制优化是其中一种的优化方法。举个例子,第 0 种物品有 7 个,我们该如何拆分呢,拆成 7 个1 ?每个体积和价值都是 v0,w0。这样的计算量大概,O^2 也就是双重循环,1000 * 2000 * 2000 大概 2* 10^9, 1s 的时间限制大概能完成10^6~10^7,这样会超时的。
Alice: 是的,直接拆,拆出来的物品数量太多了
Bob: 这样其实就转换成了拆分的问题,把 7 拆成若干个数字,且这些数字能组成 0-7 的所有数字。
Alice: 哦哦,就是二进制啊,二进制是能够表达所有整数的,0到7也就是,2^1 , 2^1, 2^2 这些。然后其实就是二进制的表示一样,7 就是 111,对应到三个物品,就是全选 ?
Bob: 对,但是还有一个问题,如果你的数字是 8 呢,拆成 1,2, 4,8 ?那样的话,就有可能选出 1+2 + 4 + 8 == 15 的选择,但是原来最多也就是 8个。
Alice: 可以这样子,8 的数字就用 7 的那套,剩下的差值额外补齐,0-7 的范围再加个 1,所能表达的范围就是 0-8。
Bob: 应该就是这样,然后具体拆分的时候还可以直接从 1,2,4 累乘,然后不断地减下来,最后剩下的额外加一套。这样应该比较方便而且很快。
Alice:nice,拆外之后直接用 01 背包就行了。这样算的计算量应该是 log 2000 * 1000 * 2000 == 2.2 * 10^7 ,应该没问题啦。
Bob:单调队列优化呢 ?
Alice: 这个看起来很麻烦的样子,是啊,这个需要先知道单调队列是啥。可以先看一下 这篇文章
Bob:单调队列优化的思路大概是这样的,还得从完全背包的递推公式讲起,考虑第 i 种物品 dp[j] = max(dp[j], dp[j-vi * k] + wi * k) k 取值 0,1,2,3 …。这里实际的计算过程是什么样的呢,j-vi*k 减到最后,无论 j 的取值是啥,一定剩下的是 vi 的各种余数,1,2,3 … vi-1,然后从 1+v,1+2v,1+3v … 的状态转移计算过程会相互影响,而 2+v,2+2v,2+3v 会相互影响,两个余数之间的计算过程互相不影响,这样我们就能把对 i 物品的计算划分为互相独立的 vi-1 个,然后单独计算。
Alice: 然后的,拆分成 多个计算过程就能变快 ?并行处理吗 ?
Bob: 然后就是难以理解的地方了,我先举个例子吧,假设背包体积是 100, 第 i 种物品的体积是 5,价值是 4,数量是 3,考虑第 i 个物品时候的状态的计算,dp[j] = max(dp[j- 5*0] + 4*0, dp[j- 5*1] + 4*1, dp[j-5*2] + 4*2), dp[j - 5*3] + 4*3,具体的计算过程,从底向上就是 求 dp[0 + 5*0], dp[0 + 5*1] + 4*1, dp[0 + 5*2] + 4*2, dp[0 + 5*3] + 4*3 之间的最大值,然后再根据放 1 个,2个,3个求出 dp[0+20] 而 dp[1+20] 看的是 dp[1 + 5*0] + 4*0, dp[1 + 5*1] + 4*1, dp[1 + 5*2] + 4*2, dp[1 + 5*3] + 4*3 的最大值。明白了吗 ? 0,1,2 在这里就是不同的计算序列,每个计算序列都要根据 4 的滑动窗口求前面的最大值,然后再计算当前的最大值。
Alice: 滑动窗口就在这呢,原来是对第 i 种物品的体积余数的每个计算序列里面滑动,滑动窗口的大小就是物品的最大数量。
Bob: 其实滑动窗口的大小不一定是物品的最大数量,k 的实际取值范围是 math.min (si + 1, maxVolum / vi),不过这个可以在代码层直接实现掉,可以暂时认为是最大数量,不影响理解。
Alice: 然后单调队列里面维护的时候什么呢 ?队首和队尾都是怎么维护的呢 ?
Bob: 单调队列里面维护的是当前窗口里面最大价值所对应的体积,这样我们应该能够比较轻松的写出 dp[j] 的更新,dp[j] = lastRowDp[queue[0]] + (j - queue[0]) / vi * wi,想一下,queue[0] 里面是当前窗口的最大价值对应的体积,我们在这个体积之上更新 dp[j]。队首的维护其实还是窗口的大小,只不过这里窗口的大小是通过体积的计算来校验的。
Alice: 这些都还好理解,那队尾的维护呢 ?我记得滑动窗口最大值里面是直接计算窗口里面的数字之和,这里应该不是吧。
Bob: 确实不是,这里还有点不太好理解。这里还是按照最大价值来计算的,只是比较的是第 i-1 个物品对应的体积和 第 i 个物品对应的体积所能给 dp[j] 带来的价值收益。要知道我们在 queue[0] 队首的位置维护的是在窗口中能给 dp[j] 带来最大价值的体积,而单调队列的维护正式通过队首和队尾维护的,所以队尾的维护逻辑实际和 dp[j] 的更新逻辑是一致的。
Alice: 更新逻辑是一致的 ?!我好像有点明白了。还有一些细节问题,滑动窗口的大小不定是怎么实现的 ?
Bob: 这个好说,你从余数 r 开始,r 就是 r + 0 * vi 然后每次给 r += vi,让 r 不要超过最大体积就可以了。
Alice: 这题真难。
Bob:这题真难,我看别人的题解看了半天才明白滑动窗口在哪滑呢,看别人代码看了半天,单调队列维护的代码都快背下来了,也没看明白怎么维护的,还是得实际举个例子。
Alice: 还有一个小问题,这里为啥不能把状态压缩成一个一位数组,为啥还要一个 lastRowDp 呢 ?
Bob:简单,第 i 个物品的 dp[j] 的更新需要依赖于体积 j 的前 si 个状态,如果直接用 dp[j - vi],那用的就是更新过的值了,就不是 i-1 个物品的状态了。
代码:
暴力
const solve = (count, maxVolum, volumAndWeight) => {const dp = new Array(maxVolum + 1).fill(0);for(let i=0; i<count; ++i){// 第 i 个物品的体积和价值const [ivolum, iweight, itotal] = volumAndWeight[i];for(let j=maxVolum; j>=ivolum; --j) {const candiantes = [];for(let k=0; k<=itotal; ++k) {j - ivolum * k >= 0 && candiantes.push(dp[j - ivolum * k] + k * iweight);}dp[j] = Math.max(...candiantes);}}console.log(dp[maxVolum]);
}
二进制优化
const solve = (count, maxVolum, volumAndWeightAndCount) => {// 二进制拆分为 01 背包const volumnAndWeight = [];volumAndWeightAndCount.forEach(item => {let [v, w, s] = item;for (let k=1; k <= s; k*=2) {s -= k;volumnAndWeight.push([k*v, k*w]);}if(s > 0) {volumnAndWeight.push([s*v, s*w]);}});// 01 背包解法const dp = new Array(maxVolum + 1).fill(0);for(let i=0; i<volumnAndWeight.length; ++i){// 第 i 个物品的体积和价值const [ivolum, iweight] = volumnAndWeight[i];for(let j=maxVolum; j>=ivolum; --j) {dp[j] = Math.max(dp[j], dp[j - ivolum] + iweight);}}console.log(dp[maxVolum]);
}
单调队列优化
const fs = require('fs');
let buffer = '';process.stdin.on('readable', () => {const chunk = process.stdin.read();if (chunk) {buffer += chunk.toString()}
});// 输入的字符串转换为数字
const convert = (inputString) => {const list = [];inputString.split('\n').forEach((line) => {const tokens = line.split(' ');list.push(tokens.map(num => parseInt(num, 10)));});return list;
}// 批量调用
const batchCall = (list, solve) => {// 划分数据const data = [];let countAndVolumIndex = 0;while(countAndVolumIndex < list.length) {const [count, volum] = list[countAndVolumIndex];data.push({volum: volum,count: count,volumAndWeightAndCount: list.slice(countAndVolumIndex + 1, countAndVolumIndex + 1 + count)});countAndVolumIndex += count + 1;}data.forEach(item => {if(solve && item && item.count && item.volum) {solve(item.count, item.volum, item.volumAndWeightAndCount);}});
}const solve = (count, maxVolum, volumAndWeightAndCount) => {// 单调队列优化方法const dp = new Array(maxVolum + 10).fill(0);// 对于每种物品 for (let i=0; i<count; ++i) {// 状态压缩const lastRowDp = [...dp];// 取出第 i 种物品的体积,价值,数量const [vi, wi, si] = volumAndWeightAndCount[i];// 对于每种可能剩余的体积,0,1,2, ... vi-1 for (let r=0; r<vi; ++r) {// 单调队列求解每种可能的最大值,滑动窗口大小是,math.min (si, maxVolum / vi) 下取整// 0 + 0v, 0 + 1v, 0 + 2v ... 0 + kv 的数组中滑动,每次一步// 最大价值对应的体积的单调队列,双端队列const queue = [];for(let j=r; j<=maxVolum; j+=vi) {// 维护队首// i 物品的体积超了,注意这里是大于而不是大于等于,要把 r+0*vi也包括进来while(queue.length && j-queue[0] > vi*si) {queue.shift();}// 维护队尾while(queue.length && lastRowDp[queue[queue.length-1]] + (j - queue[queue.length-1]) /vi * wi <= lastRowDp[j]) {queue.pop();}// 入队queue.push(j);// 更新 dpdp[j] = lastRowDp[queue[0]] + (j-queue[0]) / vi * wi;}}}console.log(dp[maxVolum]);
}process.stdin.on('end', function() {batchCall(convert(buffer), solve)
});
参考:
- 题目链接-多重背包1
- 题目链接-多重背包2
- 题目链接-多重背包3
- 参考题解
相关文章:

背包问题学习笔记-多重背包问题
题意描述: 有 N 种物品和一个容量是 V 的背包。第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。 输出最大价值。输入格式 第一行两个整数…...

Net相关的各类开源项目
Net相关的各类开源项目 WPFHandyControlLive-ChartsWPFDeveloperswpf-uidesignStylet WebScheduleMasterYiShaAdminBlog.CoreNebula.AdminNewLife.CubeOpenAuth UnityuGUIUnityCsReferenceEpitomeMyUnityFrameWorkKSFrameworkTowerDefense-GameFramework-Demo 通用ClientServer…...
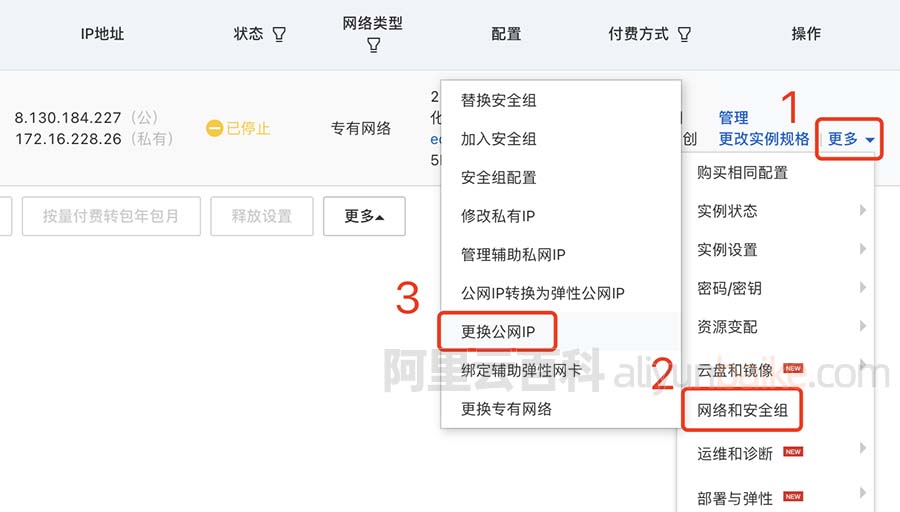
阿里云服务器修改IP地址的两种方法
阿里云服务器可以更换IP地址吗?可以的,创建6小时以内的云服务器ECS可以免费更换三次公网IP地址,超过6小时的云服务器,可以将公网固定IP地址转成弹性EIP,然后通过换绑EIP的方式来更换IP地址。阿里云服务器网分享阿里云服…...

SpringMVC的数据绑定
一、前言 SpringMVC的数据绑定是指将HTTP请求参数绑定到Java对象上。这样可以方便地从请求中获取数据并将其传递给业务逻辑。在SpringMVC中,可以使用RequestParam和ModelAttribute等注解来实现数据绑定。 二、使用RequestParam注解 RequestParam注解用于将请求参…...

1.1.OpenCV技能树--第一单元--OpenCV简介
目录 1.文章内容来源 2.OpenCV简介 3.课后习题代码复现 4.易错点总结与反思 1.文章内容来源 1.题目来源:https://edu.csdn.net/skill/practice/opencv-77f629e4593845b0bf97e74ca8ec95ae/8292?languageopencv&materialId20807 2.资料来源:https://edu.csdn.net/skill…...

transformer不同的包加载模型的结构不一样
AutoModel AutoModelForTokenClassification 结论: AutoModel加载的模型与AutoModelForTokenClassification最后一层是不一样的,从这个模型来看,AutoModelForTokenClassification加载的结果是对的 问题: 为什么AutoModel和Aut…...
【MyBatis-Plus】快速精通Mybatis-plus框架—核心功能
刚才的案例中都是以id为条件的简单CRUD,一些复杂条件的SQL语句就要用到一些更高级的功能了。 1.条件构造器 除了新增以外,修改、删除、查询的SQL语句都需要指定where条件。因此BaseMapper中提供的相关方法除了以id作为where条件以外,还支持…...

C语言:选择+编程(每日一练Day9)
目录 选择题: 题一: 题二: 题三: 题四: 题五: 编程题: 题一:自除数 思路一: 题二:除自身以外数组的乘积 思路二: 本人实力有限可能对…...

蓝桥等考Python组别十三级003
第一部分:选择题 1、Python L13 (15分) 运行下面程序,输出的结果是( )。 t = (1, 2, 2, 1, 4, 3, 2) print(t.count(2)) 1234正确答案:C 2、Python L13 (...

2023年CSP-J真题详解+分析数据(选择题篇)
目录 前言 2023CSP-J江苏卷详解 小结 前言 下面由我来给大家讲解一下CSP-J的选择题部分。 2023CSP-J江苏卷详解 1.答案 A 解析:const在C中是常量的意思,其作用是声明一个变量,值从头至尾不能被修改 2.答案 D 解析:八进制…...
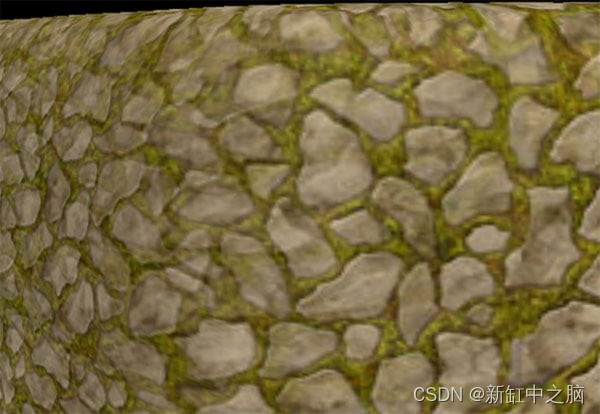
基于三平面映射的地形纹理化【Triplanar Mapping】
你可能遇到过这样的地形:悬崖陡峭的一侧的纹理拉伸得如此之大,以至于看起来不切实际。 也许你有一个程序化生成的世界,你无法对其进行 UV 展开和纹理处理。 推荐:用 NSDT编辑器 快速搭建可编程3D场景 三平面映射(Trip…...
初步了解nodejs语法和web模块
在此, 第一个Node.js实例_js firstnode-CSDN博客 通过node运行一个简单的server.js,实现了一个http服务器; 但是还没有解析server.js的代码,下面看一下; require 指令 在 Node.js 中,使用 require 指令来…...
51单片机+EC11编码器实现可调参菜单+OLED屏幕显示
51单片机+EC11编码器实现可调参菜单+OLED屏幕显示 📍相关篇《stc单片机使用外部中断+EC11编码器实现计数功能》 🎈《STC单片机+EC11编码器实现调节PWM输出占空比》 🌼实际操作效果 🍁整个项目实现框架: 📓EC11接线原理图: 📓项目工程简介 📝仅凭借一个EC11编…...
数据结构刷题训练——二叉树篇(一)
📙作者简介: 清水加冰,目前大二在读,正在学习C/C、Python、操作系统、数据库等。 📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。 欢迎点赞 👍…...
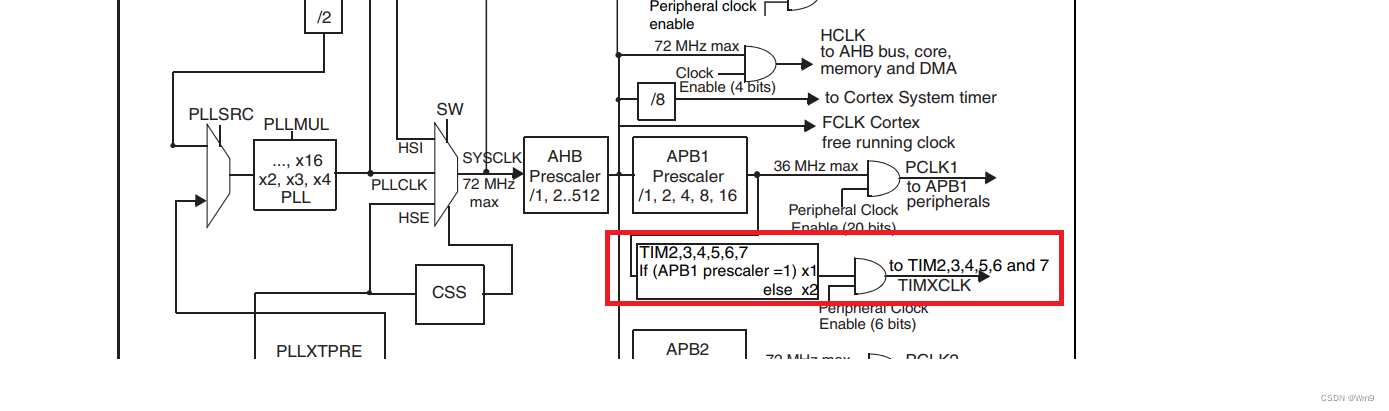
2023版 STM32实战5 基本定时器中断
基本定时器简介与特性 -1-时钟可分频 -2-计数模式只可以选择累加 -3-只可以用来定时(含中断) 查看时钟源 如图定时器7的时钟最大为72MHZ 定时时间的计算 通用定时器的时间计算公式为 Tout ((arr1)(psc1&…...

css3实现页面元素抖动效果
html <div id"shake" class"shape">horizontal shake</div>js(vue3) function shake(elemId) {const elem document.getElementById(elemId)console.log(获取el, elem)if (elem) {elem.classList.add(shake)setTimeou…...
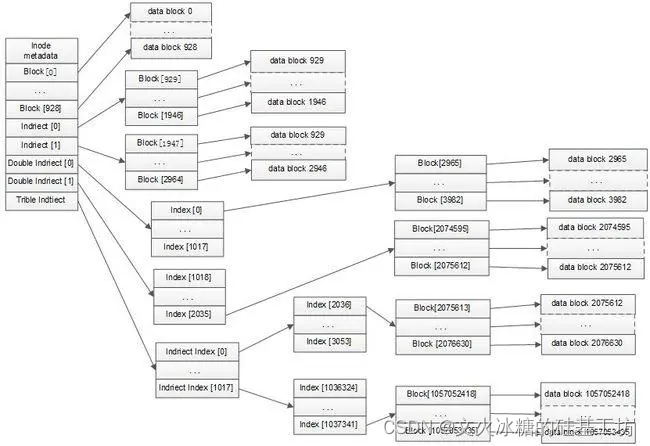
[架构之路-232]:操作系统 - 文件系统存储方法汇总
目录 前言: 一、文件系统存储方法基本原理和常见应用案例: 二、Windows FAT文件系统 2.1 概述 三、Linux EXT文件系统 3.1 基本原理 3.2 索引节点表(Inode Table) 3.2.1 索引节点表层次结构 3.2.2 间接索引表的大小和表项…...

简述 AOP 动态代理
一、AopAutoConfiguration 源码: Configuration(proxyBeanMethods false) ConditionalOnProperty(prefix "spring.aop", name "auto", havingValue "true", matchIfMissing true) public class AopAutoConfiguration {Configur…...
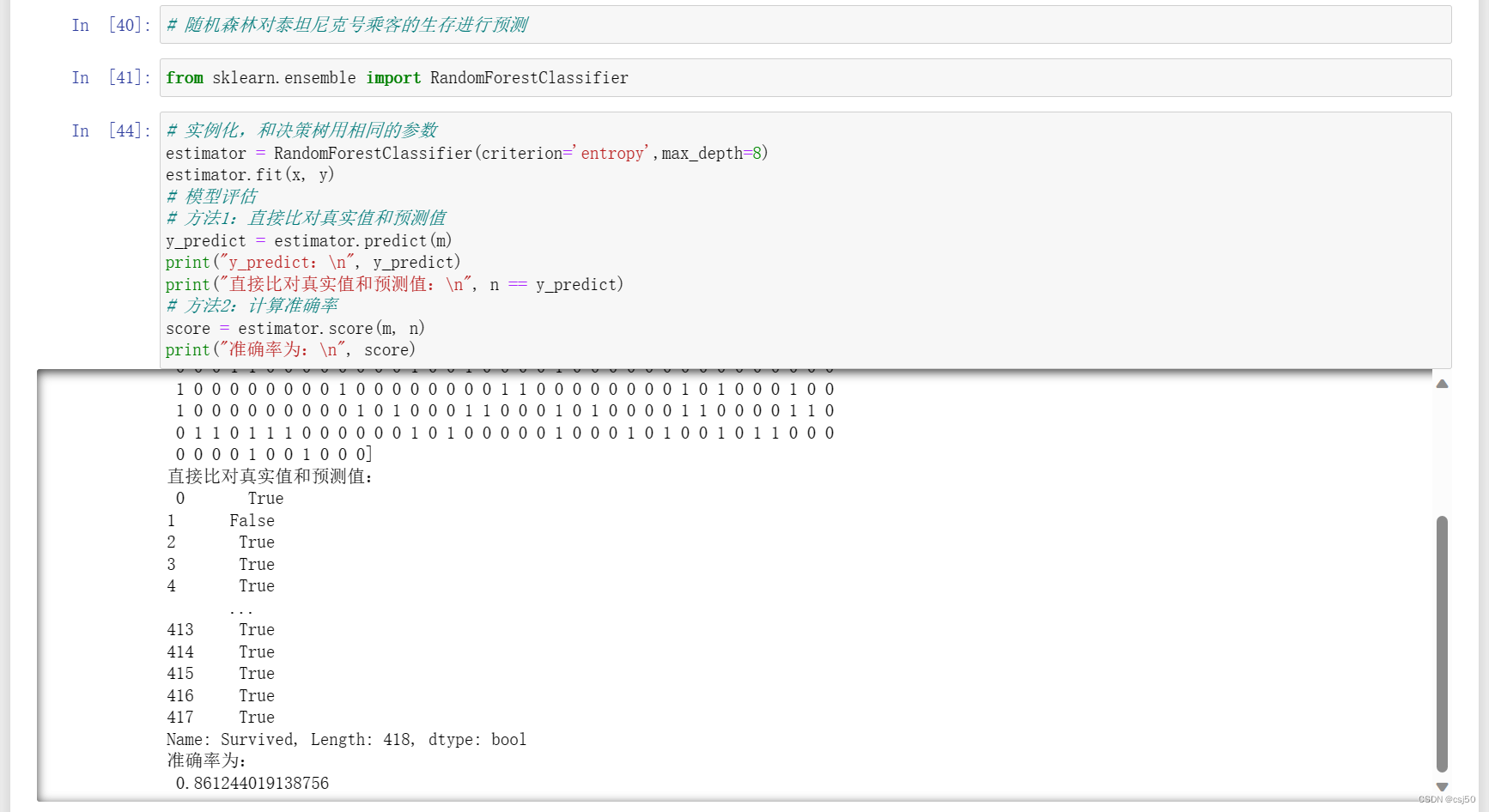
机器学习基础之《分类算法(8)—随机森林》
一、什么是集成学习方法 1、定义 集成学习通过建立几个模型组合的来解决单一预测问题。它的工作原理是生成多个分类器/模型,各自独立地学习和作出预测。这些预测最后结合成组合预测,因此优于任何一个单分类的做出预测 谚语:三个臭皮匠顶个诸…...

Python数据攻略-Pandas进行CSV和Excel文件读写
在数据分析的世界里,能够读取和写入不同格式的文件是一项基本而重要的技能。CSV(逗号分隔值)和Excel是两种常见的数据存储格式。它们在商业、科研、教育等多个领域都有广泛应用。 文章目录 读取CSV文件`pd.read_csv()` 文件读取函数的基本用法`DataFrame.to_csv()` 数据写入…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
