机器学习基础之《分类算法(8)—随机森林》
一、什么是集成学习方法
1、定义
集成学习通过建立几个模型组合的来解决单一预测问题。它的工作原理是生成多个分类器/模型,各自独立地学习和作出预测。这些预测最后结合成组合预测,因此优于任何一个单分类的做出预测
谚语:三个臭皮匠顶个诸葛亮、众人拾柴火焰高
二、什么是随机森林
1、定义
在机器学习中,随机森林是一个包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定
森林:包含多个决策树的分类器
2、什么是众数
例如,如果你训练了5个树,其中有4个树的结果是True,1个数的结果是False,那么最终投票结果就是True
三、随机森林原理过程
1、如何随机
我们都是根据特征值和目标值进行预测的
我们面临的训练集是一致的,如何对同样的训练集去产生多棵树呢
两个随机:
训练集随机
特征随机
训练集:有N个样本,M个特征
2、训练集随机
bootstrap:随机有放回抽样
例子:[1, 2, 3, 4, 5]
新的树的训练集:
[2, 2, 3, 1, 5],先抽到2,把2放回去,可能又抽到2,把2放回去,抽到3,把2放回去。。。以此类推
从N个样本中随机有放回的抽样N个
3、特征随机
从M个特征中随机抽取m个特征
M >> m
4、算法归纳
训练集:有N个样本,M个特征
(1)从N个样本中随机有放回的抽样N个
(2)从M个特征中随机抽取m个特征,并且M 要远远大于 m
(3)M >> m,起到了降维的作用
5、为什么要这样做
因为笨的树都在乱蒙,聪明的树结果总是相同,最终会实现投票的众数结果是相对正确的
四、API
1、class sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)
随机森林分类器
n_estimators:设定要选几颗树,可选,默认=10,森林里的树木数量 120,200,300,500,800,1200
criterion:划分决策树的依据,可选,默认='gini'(基尼系数)
max_depth:树的深度,可选,默认=None 5,8,15,25,30
bootstrap:可选,默认=True,是否在构建树时使用放回抽样
max_features;默认=auto,每个决策树的最大特征数量,从M个特征中选择m个特征
If "auto", then max_features=sqrt(n_features).
If "sqrt", then max_features=sqrt(n_features) (same as "auto").
If "log2", then max_features=log2(n_features).
If None, then max_features=n_features.
min_samples_split:节点划分最少样本数
min_samples_leaf:叶子节点的最小样本数
五、随机森林预测案例
1、代码
在前一篇决策树的代码后面加上:
# 随机森林对泰坦尼克号乘客的生存进行预测from sklearn.ensemble import RandomForestClassifier# 实例化,和决策树用相同的参数
estimator = RandomForestClassifier(criterion='entropy',max_depth=8)
estimator.fit(x, y)
# 模型评估
# 方法1:直接比对真实值和预测值
y_predict = estimator.predict(m)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", n == y_predict)
# 方法2:计算准确率
score = estimator.score(m, n)
print("准确率为:\n", score)
2、运行结果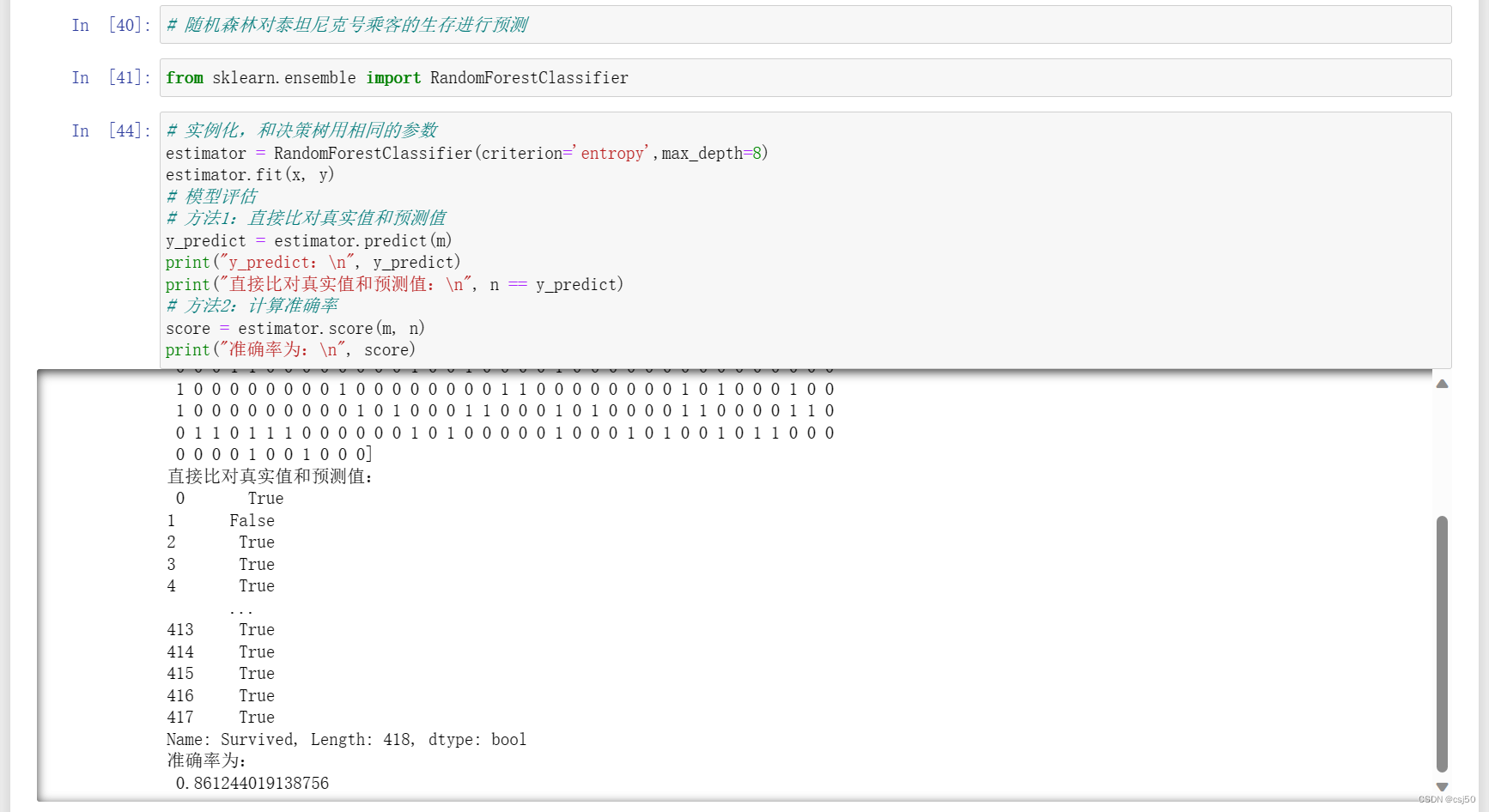
回顾下:
x是训练集的特征值,y是训练集的目标值,m是测试集的特征值,n是测试集的目标值
但是对比决策树的94%准确率,随机森林反而降低了
六、总结
1、在当前所有算法中,具有极好的准确率
2、能够有效地运行在大数据集上,处理具有高维特征的输入样本,而且不需要降维
3、能够评估各个特征在分类问题上的重要性
相关文章:

机器学习基础之《分类算法(8)—随机森林》
一、什么是集成学习方法 1、定义 集成学习通过建立几个模型组合的来解决单一预测问题。它的工作原理是生成多个分类器/模型,各自独立地学习和作出预测。这些预测最后结合成组合预测,因此优于任何一个单分类的做出预测 谚语:三个臭皮匠顶个诸…...

Python数据攻略-Pandas进行CSV和Excel文件读写
在数据分析的世界里,能够读取和写入不同格式的文件是一项基本而重要的技能。CSV(逗号分隔值)和Excel是两种常见的数据存储格式。它们在商业、科研、教育等多个领域都有广泛应用。 文章目录 读取CSV文件`pd.read_csv()` 文件读取函数的基本用法`DataFrame.to_csv()` 数据写入…...

lv7 嵌入式开发-网络编程开发 13 UNIX域套接字
1 UNIX 域流式套接字 本地地址 struct sockaddr_un {unsigned short sun_family; /* 协议类型 */char sun_path[108]; /* 套接字文件路径 */ };UNIX 域流式套接字的用法和 TCP 套接字基本一致,区别在于使用的协议和地址不同 UNIX 域流式套接字服务器端…...

blender光照系统设置
0)Viewport Shading设置里面的Lighting下面的参数: Scene Lights,Scene World - Scene Lights是指在渲染模式下是否使用场景中的灯光对象来照亮物体。 - Scene World是指在渲染模式下是否使用场景中的世界设置来作为背景和环境光。如果关闭该选项&#…...
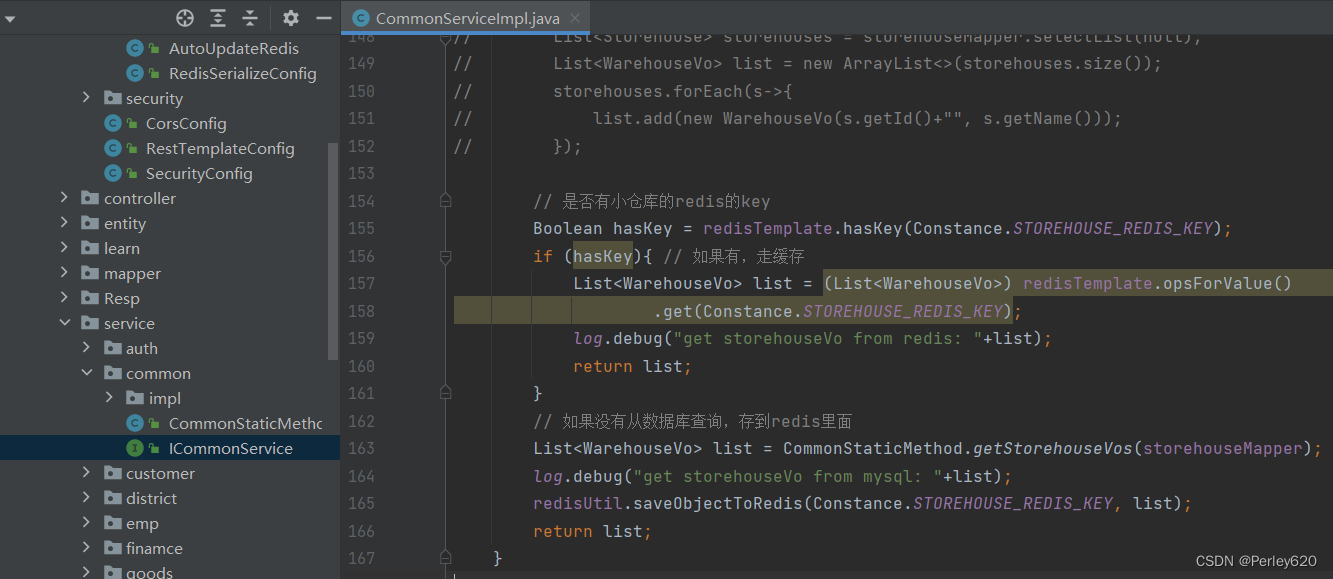
华为云云耀云服务器L实例评测|基于canal缓存自动更新流程 SpringBoot项目应用案例和源码
前言 最近华为云云耀云服务器L实例上新,也搞了一台来玩,期间遇到各种问题,在解决问题的过程中学到不少和运维相关的知识。 在之前的博客中,介绍过canal的安装和配置,参考博客 拉取创建canal镜像配置相关参数 & …...
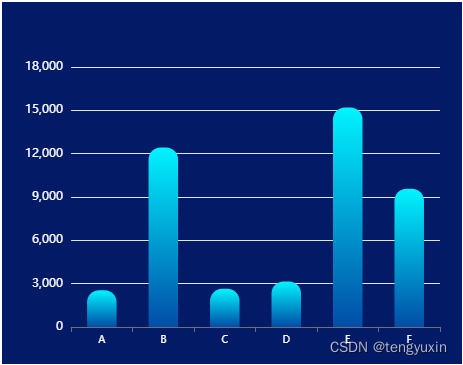
vue3 中使用echarts图表——柱状图
柱状图是比较常用的图形结构,所以我先收集一些精美的柱状图 一、柱状图:设置圆角和颜色 <template><div class"box" ref"chartDom"></div> </template> <script setup> import { ref, onMounted } fr…...

基于Java的家政公司服务平台设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...
深入了解 PostgreSQL:功能、特性和部署
PostgreSQL,通常简称为Postgres,是一款强大且开源的关系型数据库管理系统(RDBMS),它在数据存储和处理方面提供了广泛的功能和灵活性。本文将详细介绍 PostgreSQL 的功能、特性以及如何部署和使用它。 什么是 PostgreSQ…...
平台项目列表页实现(二)
这里写目录标题 一、顶部盒子设计1. 顶部盒子包含项目列表和添加项目、退出登录2个按钮 二、项目列表盒子设计三、添加项目盒子设计四、退出登录功能实现五、路由导航守卫实现六、展示项目信息七、bug修复1、当项目名称太长或者项目负责人太长,需要一行展示…...

osg实现鼠标框选
目录 1. 需求的提出 2. 具体实现 2.1. 禁止场景跟随鼠标转动 2.2. 矩形框前置绘制 3. 附加说明 3.1. 颜色设置说明 3.2.矩形框显示和隐藏的另一种实现 1. 需求的提出 有时需要在屏幕通过按住键盘上的某个键如Ctrl键且按住鼠标左键,拖出一个矩形,实现框…...
)
电路原理解题笔记(一)
文章目录 贼基础的知识等效电阻基尔霍夫电流定律电阻电路的一般分析支路电流法节点电压法回路电流法 电路定理叠加定理戴维宁等效电路诺顿等效电路求某电阻值为多少可吸收最大功率。吸收、释放功率 第一个月,对应猴博士的一到五课时。 贼基础的知识电阻电路的等效变…...
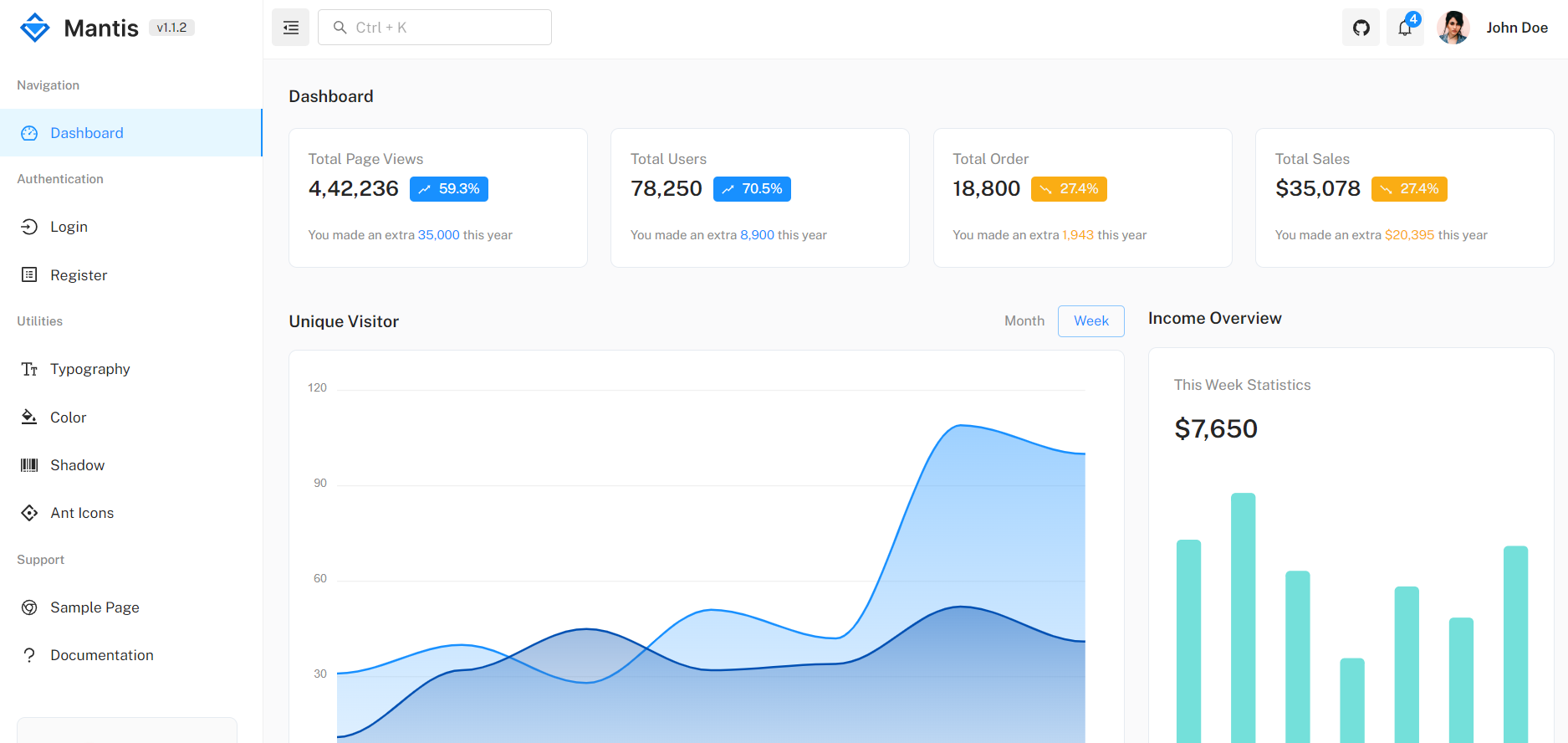
分享几个优秀开源免费管理后台模版,建议收藏!
大家好,我是 jonssonyan 今天和大家分享一些免费开源的后台管理页面,帮助大家快速搭建前端页面。为什么要用模板?道理很简单,原因是方便我们快速开发。我们不应该花太多的时间在页面调整上,而应该把精力放在核心逻辑和…...

BFS模板:844. 走迷宫
给定一个 nmnm 的二维整数数组,用来表示一个迷宫,数组中只包含 00 或 11,其中 00 表示可以走的路,11 表示不可通过的墙壁。 最初,有一个人位于左上角 (1,1)(1,1) 处,已知该人每次可以向上、下、左、右任意…...
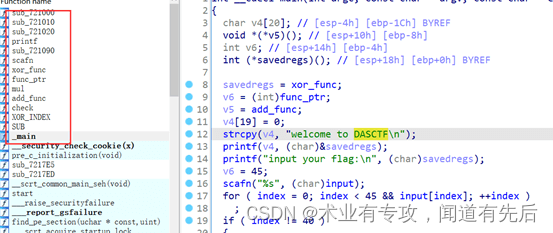
re学习(37)DASCTF 2023 0X401七月暑期挑战赛 controflow
程序通过改变栈里面的返回地址来控制程序的控制流 从而达到混淆的效果 左侧有许多被hook的函数 在每个函数开头设置断点 然后观察程序的运行流程 会发现输入的数据会进行 异或 相加 异或 相减 相乘 异或等操作 要注意部分运算的索引是 从[10]开始的 具体思路参考…...
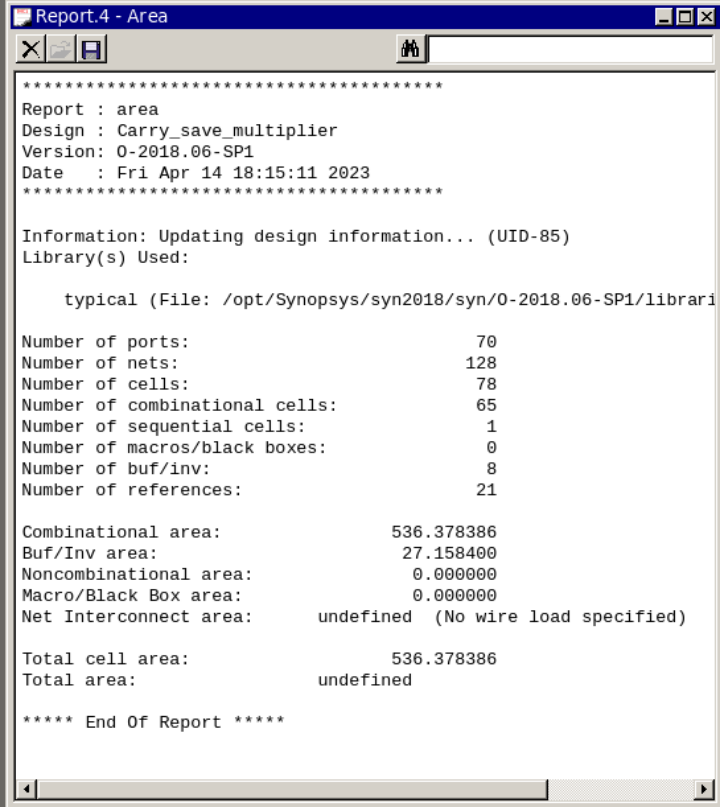
数字IC前端学习笔记:数字乘法器的优化设计(进位保留乘法器)
相关阅读 数字IC前端https://blog.csdn.net/weixin_45791458/category_12173698.html?spm1001.2014.3001.5482 阵列乘法器设计中限制乘法器速度的是随着数据位宽而迅速增大的串行进位链,如果使用进位保留加法器,则可以避免在设计中引入较长时间的等待&…...

prority_queue的学习
优先级队列(Priority Queue)是一种抽象数据类型,它类似于普通的队列或堆栈,但每个元素都有一个关联的优先级,这个优先级决定了元素在队列中的位置和被访问的顺序。在优先级队列中,具有最高优先级的元素通常…...
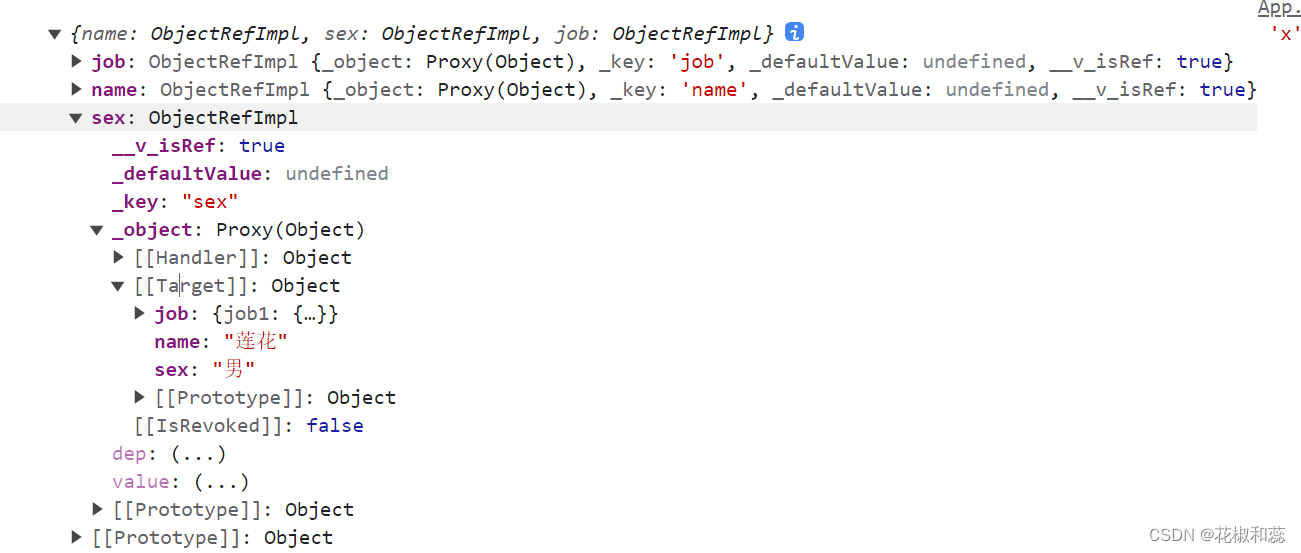
【vue3】toRef与toRefs的使用,toRef与ref的区别
假期第四篇,对于基础的知识点,我感觉自己还是很薄弱的。 趁着假期,再去复习一遍 1、toRef与toRefs 创建一个ref对象,其value值指向另一个对象中的某个属性 语法:const name toRef(person,‘name’…...

信息论基础第二章部分习题
2.5 证明若H(Y|X)0,则Y是X的函数 若 H ( Y ∣ X ) 0 H(Y|X) 0 H(Y∣X)0,意味着在已知 X X X 的条件下, Y Y Y 的不确定性为零,即给定 X X X 的值,我们完全确定了 Y Y Y 的值。这表明 Y Y Y 的取值完全由 X X…...

信息化发展73
数字经济 数字经济是继农业经济、工业经济之后的更高级经济形态。从本质上看,数字经济是一种新的技术经济范式,它建立在信息与通信技术的重大突破的基础上,以数字技术与实体经济融合驱动的产业梯次转型和经济创新发展的主引擎,在…...

560. 和为 K 的子数组
题目描述 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。 示例 1: 输入:nums [1,1,1], k 2 输出:2示例 2: 输入:nums [1,2,3], k 3 输出:2…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...
