假期题目整合
1.
下载解压题目查看即可

典型的猪圈密码只需要照着输入字符解开即可得到答案
2.
冷门类型的密码题型,需要特意去找相应的解题思路,直接百度搜索天干地支解密即可

3.

一眼能出思路他已经给了篱笆墙的提示提示你是栅栏密码对应解密即可
4.
最简单的社会主义密码解密搜索相应的解密即可
5.
它没用给思路需要自己去一个一个试,最后试出来试md5解密

6.

他给你提示是base64,需要写个脚本,一般建议去找gpt帮你写一个及快速又方便

7.


本题是比较难的但是它给了题目标签利用在线的unencode解密网站在线解密即可,我相信如果没有提示的话一般不太可能能解出来,主要还是见得少做的少的问题
8.

这个他给了字典一般这种情况直接扔给gpt写脚本,如果没写出来基本就做不出来了,直接下一题就行
9.

现在我觉得直接给好脚本只需要修改的都比较简单,直接gpt写就完了



10.

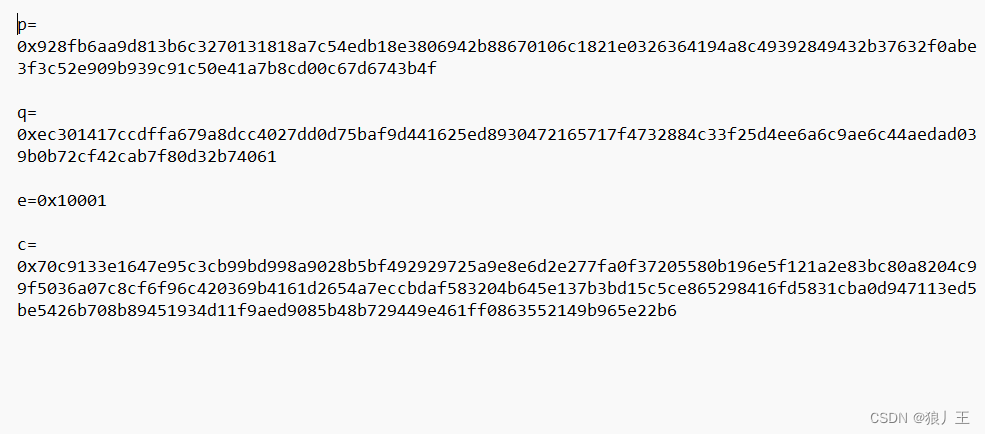
最近关于rsa解密做的比较多所以能一眼看出来是什么解密,这种他直接把所有值给好了直接写脚本即可解出来,这题的前提是要把值转化为10进制,16进制脚本是无法识别进行解密的
11.

这一道题也就是我学习解rsa解密的第一道题当时也不知道怎么搞这一类的解密,只能去看别人的wp发现没有在线解密网站,都必须自己写脚本进行解密,后面慢慢的就熟练用gpt写脚本做rsa的解密题,一般都能解出来,思路还是比较清晰的

12.
这题的难点在于他不是传统的佛语解密,是新佛语解密,我也找了老半天才知道这是新佛语解密,最开始一直以为那个网站不行
以下是新佛语网站解密链接需要自取
新约佛论禅/佛曰加密 - PcMoe!

后面一次根据思路即可注意看提示就行,后面没有太卡你的地方
13.

同样没有提示全靠自己的话比较费时间有提示的密码解密和没有提示的密码解密是两种难度,他给了base家族提示只需要我们往这个方向入手即可最后可以发现是自由base解密可以写脚本,也可以找网站解第二行有百分号这种可以先去尝试url解密

14.

这这题是传统的八卦解密但是出题人好像不是很理解八卦,导致你用gpt的跑不出来这个解密,我也是看别人的wp看别人的脚本才解出来的,这题做下来感觉收获不大,不是很建议大家去尝试,因为题目本身就有问题。

15.
简单的base64脚本解密,根据给的提示只需要将其整体向前平移五位即可得到答案

16.


签到题,base64解密
17.

这题算是一种新的解密中文电码解密,只有见过以后才会有思路往这方面想,当时各种密码都尝试过就是没找到也是看了别人wp才知道是什么解密

18.

根据提示做即可,但是gpt分解不了这么大的数字,需要你去数学在线网站上分解,也算是学到点不一样的知识,后面的就很简单照着做就行
19.
这些题以前是做过的目前还是比较有印象根据提示
这是盲文解密解出来就可有获得zip压缩包的密码得到flag,这算是杂项类型结合密码学来考虽然考了俩知识点,但是都比较简单,没有难度
20.

这一题是音频隐写,考的很基础只需要会使用工具就能做
利用这个Audacity工具即可将文件放上去将整体缩小看全貌,就能发现中间有一段摩斯密码解密接出来就行

21.

这种一般纯图片的建议先查看属性,如果没有就拖到010中寻找信息,最简单从直接搜索flag的16进制开始一次往后延申思路即可这题是很简单的搜索flag16进制

22.
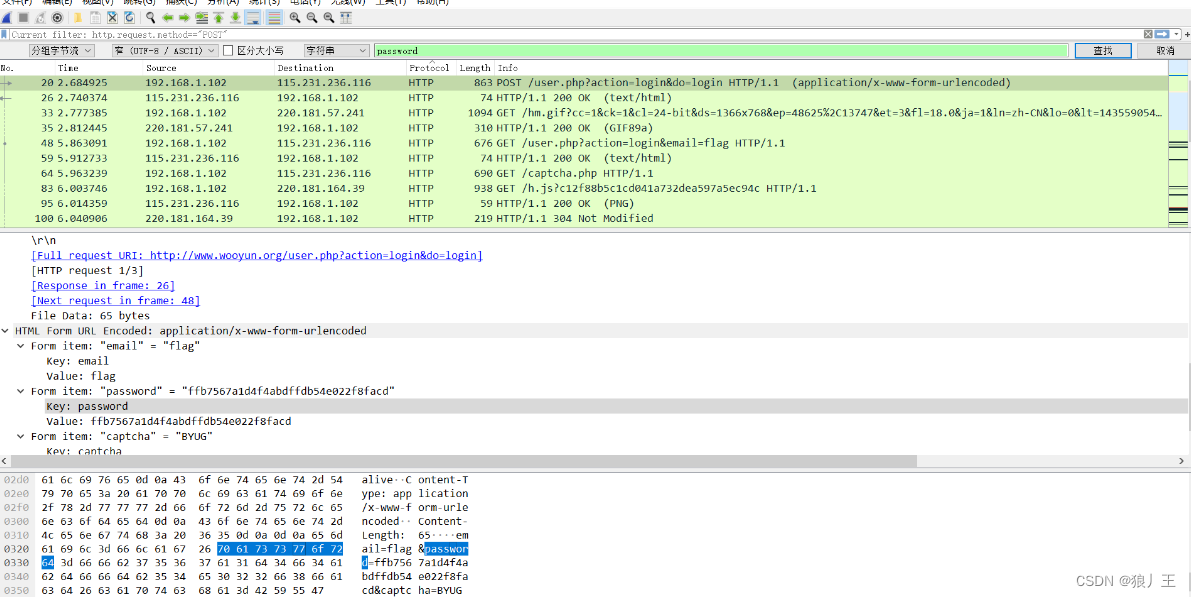
简单的wireshark使用流量分析还是得自己多存思路,自己有思路才好做这样的流量分析题目
23.
简单的图片宽高修改哪怕是不给提示也要往这一方面思考,拖入010找到宽高修改就行,操作就是先属性查看宽高,记录下来经行16进制编写,然后到010中搜索对应的16进制扩成原来的两倍即可
24.
根据提示猜测可能是F5隐写
就说明里面可能藏有额外的zip文件,有这个思路剩下的操作都不难,要么手动分解,要么kali分解都行
相关文章:

假期题目整合
1. 下载解压题目查看即可 典型的猪圈密码只需要照着输入字符解开即可得到答案 2. 冷门类型的密码题型,需要特意去找相应的解题思路,直接百度搜索天干地支解密即可 3. 一眼能出思路他已经给了篱笆墙的提示提示你是栅栏密码对应解密即可 4. 最简单的社会主…...

Redisson—分布式服务
一、 分布式远程服务(Remote Service) 基于Redis的Java分布式远程服务,可以用来通过共享接口执行存在于另一个Redisson实例里的对象方法。换句话说就是通过Redis实现了Java的远程过程调用(RPC)。分布式远程服务基于可…...
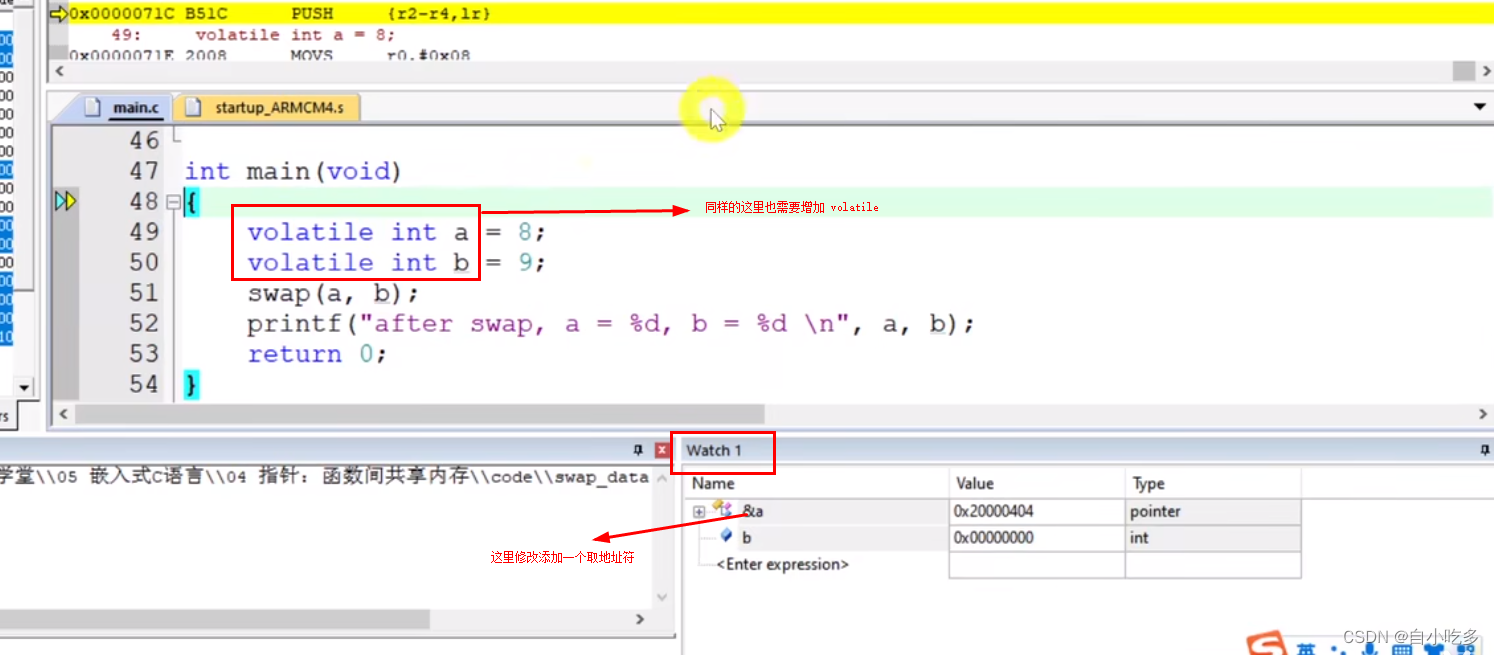
volatile使用方法
volatile使用方法 编译优化。使用等级3的话,可能将优化了一些变量。 这为什么会开启等第三呢?这是关于单片机的内存容量比较小,所以开启优化的话,可以可以省一些空间,但是如果。会出现些变量的问题,需要通过…...

提升您的 Go 应用性能的 6 种方法
优化您的 Go 应用程序 1. 如果您的应用程序在 Kubernetes 中运行,请自动设置 GOMAXPROCS 以匹配 Linux 容器的 CPU 配额 Go 调度器 可以具有与运行设备的核心数量一样多的线程。由于我们的应用程序在 Kubernetes 环境中的节点上运行,当我们的 Go 应用程…...
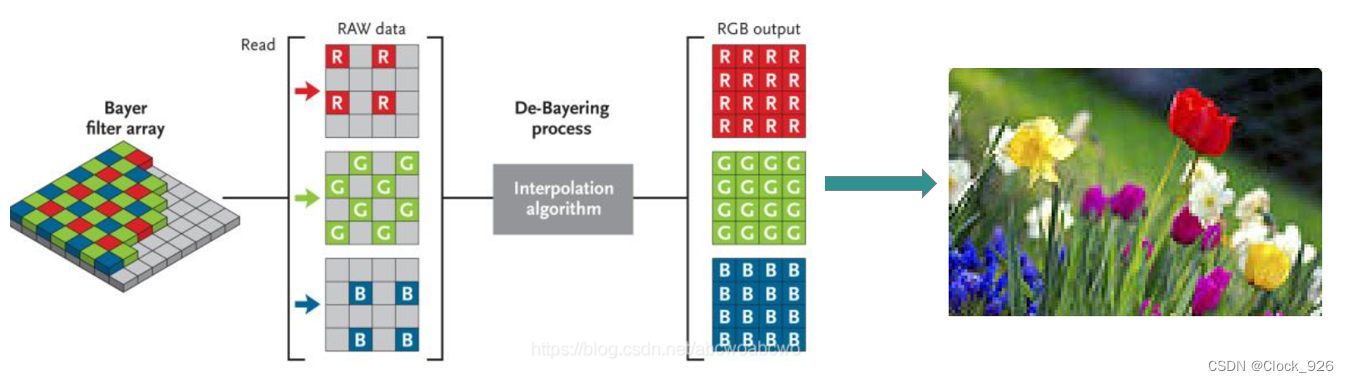
计算摄像技术02 - 颜色空间
一些计算摄像技术知识内容的整理:颜色视觉与感知特性、颜色空间和基于彩色滤镜阵列的彩色感知。 文章目录 一、颜色视觉与感知特性 (1)色调 (2)饱和度 (3)明度 二、颜色空间 (1&…...
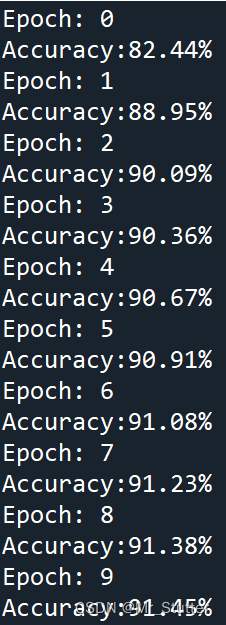
Pytorch笔记之分类
文章目录 前言一、导入库二、数据处理三、构建模型四、迭代训练五、模型评估总结 前言 使用Pytorch进行MNIST分类,使用TensorDataset与DataLoader封装、加载本地数据集。 一、导入库 import numpy as np import torch from torch import nn, optim from torch.uti…...
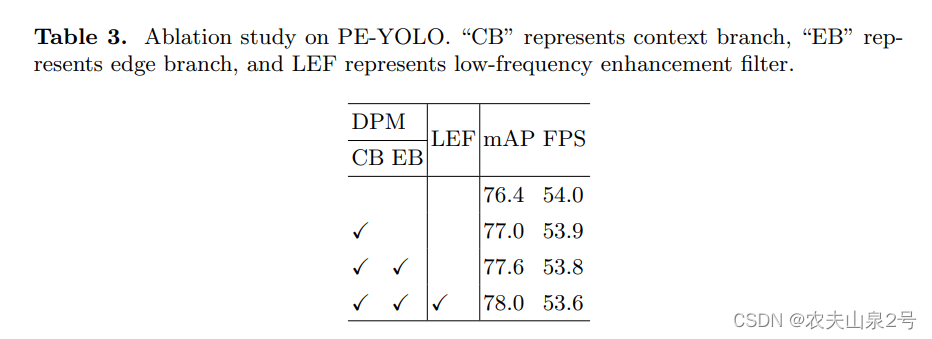
【目标检测】——PE-YOLO精读
yolo,暗光目标检测 论文:PE-YOLO 1. 简介 卷积神经网络(CNNs)在近年来如何推动了物体检测的发展。许多检测器已经被提出,而且在许多基准数据集上的性能正在不断提高。然而,大多数现有的检测器都是在正常条…...

Java 数组转集合
数组转集合 如果仅仅这样转化Arrays.asList(数组),导致集合只能查询,无法进行其他操作,因此,对该方法进行优化: List<实体> list1 new ArrayList<>(Arrays.asList(数组))以上方法就可以使用集合的所有操…...
Elasticsearch:ES|QL 查询语言简介
警告:此功能处于技术预览阶段,可能会在未来版本中更改或删除。 Elastic 将尽最大努力解决任何问题,但技术预览版中的功能不受官方 GA 功能的支持 SLA 的约束。在目前的 Elastic Stack 8.10 中此功能还没有提供。 Elasticsearch 查询语言 (ES|…...

qt qml中listview出现卡顿情况时的常用处理方法
如果在qt QML中使用ListView时出现卡顿情况,可能是因为渲染大量的数据或者在模型中进行复杂的数据处理。以下是常用的解决方法: 1. 设置ListView的缓存策略:通过设置ListView的cacheBuffer属性为适当的值,可以提高滚动的流畅性。…...

Elasticsearch基础操作演示总结
一、索引操作 (一)创建索引 创建Elasticsearch(ES)索引是在ES中存储和管理数据的重要操作之一。索引是用于组织和检索文档的结构化数据存储。 当创建Elasticsearch索引时,通常需要同时指定索引的设置(Se…...

Spring 作用域解析器AnnotationScopeMetadataResolver
博主介绍:✌全网粉丝近5W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经…...
如何发布一个 NPM 包
首先初始化: npm init 文件夹结构 .gitignore Git 库忽略文件清单.npmignore 不包括在 npm 注册库中的文件清单LECENSE 模块的授权文件README.md 说明文档bin 保存模块可执行文件的文件夹doc 保存模块文档的文件夹example 保存模块实际示例lib 保存模块代码man 保存模块的手册…...
)
Flask小项目教程(含MySQL与前端部分)
CONTENTS 1. 环境配置2. 快速搭建Flask应用程序 1. 环境配置 首先我们在项目的根目录下创建一个 Python 虚拟环境,打开命令行输入以下指令: python -m venv venv启动虚拟环境: .\venv\Scripts\Activate.ps1如果遇到报错:.\venv…...
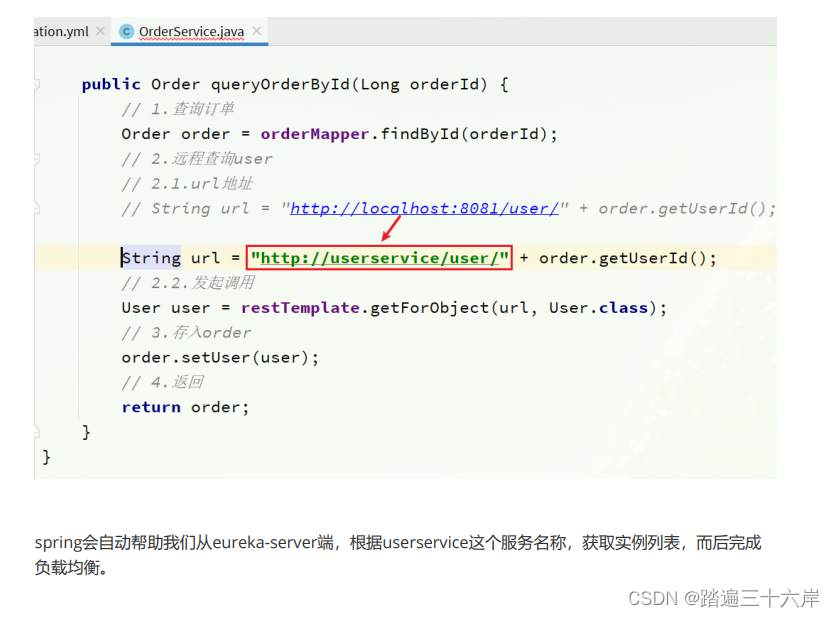
Eureka
大家好我是苏麟今天带来Eureka的使用 . 提供者和消费者 在服务调用关系中,会有两个不同的角色: 服务提供者:一次业务中,被其它微服务调用的服务。(提供接口给其它微服务) 服务消费者:一次业务…...
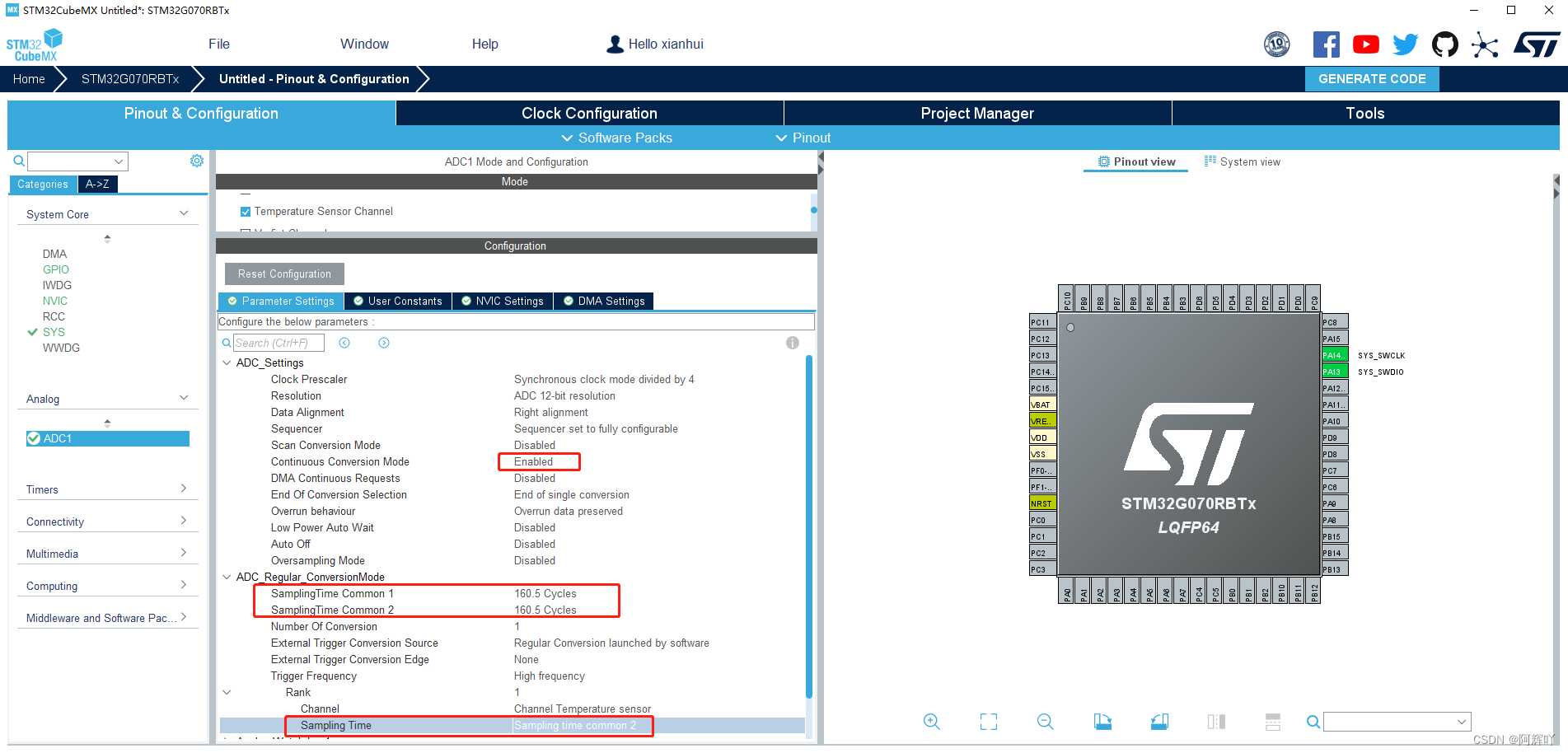
STM32G070RBT6-MCU温度测量(ADC)
1、借助STM32CubeMX生成系统及外设相关初始化代码。 在以上配置后就可以生成相关初始化代码了。 /* ADC1 init function */ void MX_ADC1_Init(void) {/* USER CODE BEGIN ADC1_Init 0 *//* USER CODE END ADC1_Init 0 */ADC_ChannelConfTypeDef sConfig {0};/* USER COD…...

数据结构之带头双向循环链表
目录 链表的分类 带头双向循环链表的实现 带头双向循环链表的结构 带头双向循环链表的结构示意图 空链表结构示意图 单结点链表结构示意图 多结点链表结构示意图 链表创建结点 双向链表初始化 销毁双向链表 打印双向链表 双向链表尾插 尾插函数测试 双向链表头插 …...

adb详细教程(四)-使用adb启动应用、关闭应用、清空应用数据、获取设备已安装应用列表
adb对于安卓移动端来说,是个非常重要的调试工具。本篇介绍常用的adb指令 文章目录 一、启动应用:adb shell am start二、使用浏览器打开指定网址:adb shell am start三、杀死应用进程adb shell am force-stop/adb shell am kill四、删除应用所…...
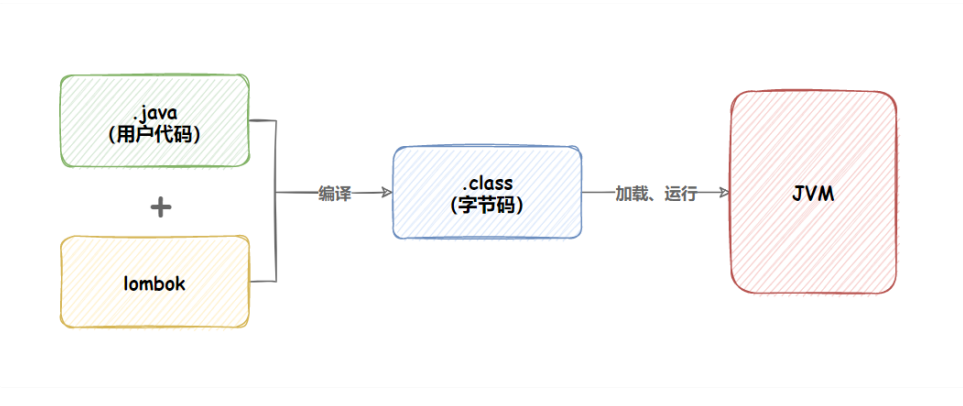
【Spring Boot】日志文件
日志文件 一. 日志文件有什么用二. 日志怎么用三. ⾃定义⽇志打印1. 在程序中得到⽇志对象2. 使⽤⽇志对象打印⽇志3. ⽇志格式说明 四. 日志级别1. ⽇志级别有什么⽤2. ⽇志级别的分类与使⽤ 五. 日志持久化六. 更简单的⽇志输出—lombok1. 添加 lombok 依赖2. 输出⽇志3. lom…...

图像处理与计算机视觉--第五章-图像分割-Canny算子
文章目录 1.边缘检测算子分类2.Canny算子核心理论2.1.Canny算子简单介绍2.2.Canny算子边缘检测指标2.3.Canny算子基本原理 3.Canny算子处理流程3.1.高斯滤波去噪声化3.2.图像梯度搜寻3.3.非极大值抑制处理3.4.双阈值边界处理3.5.边界滞后技术跟踪3.6.Canny算子边缘检测的特点 4…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
