LeetCode 377.组合总和IV 可解决一步爬m个台阶到n阶楼顶问题( 完全背包 + 排列数)
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围
示例 1:
输入:nums = [1,2,3], target = 4
输出:7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
示例 2:
输入:nums = [9], target = 3 输出:0
>>思路和分析
本题中顺序不同的序列被视为不同的组合,其实就是求排列!
(1)区分组合和排列:
组合:不强调顺序,(1,5) 和 (5,1)是同一个组合
排列:是强调顺序,(1,5) 和 (5,1)是两个不同的排列
可知本题的本质求的是排列总和,且仅仅求的是排列总和的个数,并不是把所有的排列都列出来~
若本题需要把排列都列出来的话,只能用回溯算法暴搜!
>>动规五部曲分析如下:
1.确定dp数组以及下标的含义
dp[j] : 凑成目标正整数为 j 的排列个数为 dp[j]
2.确定递归公式
dp[j] (考虑nums[i])可以由dp[j - nums[i]] (不考虑nums[i]) 推导出来
因为只要得到 nums[i],排列个数 dp[j - nums[i]],就是dp[i]的一部分
在动态规划:494.目标和 和 动态规划:518.零钱兑换II 中我们已经讲过了,求装满背包有几种方法,递推公式一般都是 dp[j] += dp[j-nums[i]]; 本题一样!
3.dp数组初始化
因为 dp[j] += dp[j - nums[i]] ,所以dp[0]要初始化为1,这样递归其他dp[j]的时候才会有数值基础
dp[0] = 1;其实是没有意义的,因为题目中说了,给定的目标值是正整数,所以dp[0] = 1是没有意义的,仅仅是为了推导递推公式。
非0下标的dp[j] 应该初始为0,这样才不会影响dp[j] 累加所有的 dp[j - nums[i]];
4.确定遍历顺序
个数是可以不限制使用的,所以本题可以使用完全背包来解决,得到的集合是排列,说明需要考虑元素之间的顺序。因为本题要求的是排列,那么需要格外注意for循环嵌套的顺序~
在动态规划:518 零钱兑换II 中讲到:
- 如果求组合数就是外层 for 循环遍历物品,内层for循环遍历背包
- 如果求排列数就是外层 for 循环遍历背包,内层for循环遍历物品
举个例子:计算dp[4]时,结果集想要有{1,3},{3,1}这两个集合,那么得先遍历背包,再遍历物品,才可以;反之则结果集只有{1,3}这样的集合。
因此可以确定本题遍历顺序最终的遍历顺序为:target(背包)放在外循环,将nums(物品)放在内循环,内循环从前向后遍历(完全背包)
5.举例来推导dp数组

class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target+1,0);dp[0] = 1;// 排列数for(int j = 0;j <= target;j++) { // 背包for(int i=0;i < nums.size();i++) { // 物品if(j >= nums[i] && dp[j] < INT_MAX - dp[j - nums[i]])dp[j] += dp[j-nums[i]];}}return dp[target];}
};// [0-i] 装满背包为j 有dp[j]种
// dp[j] += dp[j-nums[i]]- 时间复杂度:O(target * n),其中 n 为nums的长度
- 空间复杂度:O(target)
C++测试用例有两个数相加超过int的数据,所以需要在 if 里加上dp[j] < INT_MAX - dp[j - nums[i]]
参考和推荐文章、视频:
代码随想录 (programmercarl.com)
动态规划之完全背包,装满背包有几种方法?求排列数?| LeetCode:377.组合总和IV_哔哩哔哩_bilibili
往期文章:
完全背包 动态规划 + 一维dp数组
LeetCode 518.零钱兑换II 动态规划 + 完全背包 + 组合数
【总结】
- 求装满背包有几种方法,递归公示都是一样的,没有差别,但关键在于遍历顺序!
- 本题与动态规划:518.零钱兑换II 的区别,一个是求排列数,一个是求组合数,遍历顺序完全不同。
来自代码随想录的课堂截图!

爬楼梯拓展成一步可以爬m个台阶,这个代码怎么写?思路是怎么样的?
leetCode 70.爬楼梯 动态规划_呵呵哒( ̄▽ ̄)"的博客-CSDN博客
好问题:若一步一个台阶,两个台阶,三个台阶,直到 m 个台阶,有多少种方法爬到n阶楼顶。一步可以爬几个台阶,其实就是相当于每个物品,有多少种不同的方法可以爬到楼顶,相当于装满这个背包有多少种方法。比如:如果说我们先爬了一步再爬两步,再爬一步可到楼顶。和我们先爬一步,再爬一步,后爬了两步到了楼顶。请问这是几种爬楼梯的方法?很明显,这是两种方法,所以说爬楼梯的话,我们求的这个集合的个数,我们要强调元素的顺序,所以说和本题(leetCode 377.组合总和IV)是一样的。同样是强调元素之间的顺序的,也就是说 {1,2,1} 和 {1,1,2} 这是两个集合,要分别来计数。
class Solution {
public:int climbStairs(int n) {vector<int> dp(n + 1,0);dp[0] = 1;int m = 2;// m 表示一步最多可以爬多少个台阶for(int j = 1;j <= n; j++) { // 背包for(int i = 1;i <= m; i++) { // 物品if(j >= i)dp[j] += dp[j-i];}}return dp[n];}
};代码中m表示最多可以爬m个台阶,代码中把m改成2就是本题70.爬楼梯可以AC的代码了。
相关文章:

LeetCode 377.组合总和IV 可解决一步爬m个台阶到n阶楼顶问题( 完全背包 + 排列数)
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。 题目数据保证答案符合 32 位整数范围 示例 1: 输入:nums [1,2,3], target 4 输出:7 解释&#x…...
C中volatile总结
在CPU处理过程中,需要将内存中的数据载入到寄存器中才能计算,所以可能涉及到一个问题,如果内存中的数据被更改了,但是寄存器还是使用的旧数据,这样就会造成数据的不同步。 一、volatile关键字的作用 使用volatile关键…...
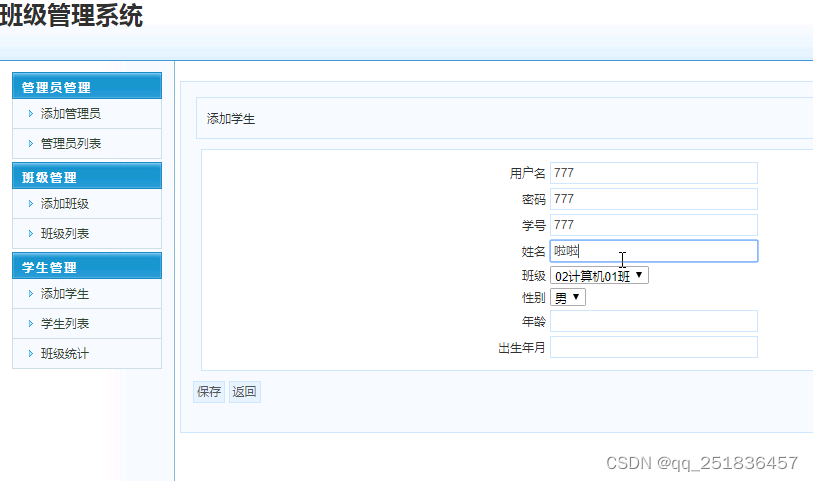
asp.net班级管理系统VS开发sqlserver数据库web结构c#编程Microsoft Visual Studio
一、源码特点 asp.net班级管理系统 是一套完善的web设计管理系统,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为vs2010,数据库为sqlserver2008,使用c#语言开发 asp.net班级管理系统 二、功能介绍 1…...
【Pytorch笔记】6.Transforms
pytorch官方文档 - transforms transforms需要使用计算机视觉工具包:torchvision。 torchvision.transforms:常用的图像预处理方法; torchvision.datasets:常用数据集的dataset实现,如MNIST、CIFAR-10、ImageNet等&am…...

nodejs+vue临沂特色产品销售平台elementui
从实际工作出发,对过去的临沂特色产品销售平台存在的问题进行分析,完善用户的使用体会。采用计算机系统来管理信息 提高了工作的效率。 随着信息化社会的形成和微电子技术日新月异的发展,临沂特色产品销售平台是针对目前临沂特色产品销售…...

机器学习必修课 - 使用管道 Pipeline
目标:学习使用管道(pipeline)来提高机器学习代码的效率。 1. 运行环境:Google Colab import pandas as pd from sklearn.model_selection import train_test_split!git clone https://github.com/JeffereyWu/Housing-prices-dat…...

WEB各类常用测试工具
一、单元测试/测试运行器 1、Jest 知名的 Java 单元测试工具,由 Facebook 开源,开箱即用。它在最基础层面被设计用于快速、简单地编写地道的 Java 测试,能自动模拟 require() 返回的 CommonJS 模块,并提供了包括内置的测试环境 …...

Naive UI 文档地址
最近几天官网访问不了,自己用github pages 部署了个 官网 github pages...

在CentOS7系统中安装MySQL5.7
第一步:下载MySQL包 > wget http://repo.mysql.com/mysql57-community-release-el7-10.noarch.rpm第二步:安装MySQL源 > rpm -Uvh mysql57-community-release-el7-10.noarch.rpm第三步:安装MySQL服务端 > yum install -y mysql-c…...
R语言通过接口获取网上数据平台的免费数据
大家好,我是带我去滑雪! 作为一名统计学专业的学生,时常和数据打交道,我深知数据的重要性。数据是实证研究的重要基础,每当在完成一篇科研论文中的实证研究部分时,我都能深刻体会实证研究最复杂、最耗时的工…...
【Docker内容大集合】Docker从认识到实践再到底层原理大汇总
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总https://blog.csdn.net/yu_cblog/categ…...
算法题:摆动序列
这道题是一道贪心算法题,如果前两个数是递增,则后面要递减,如果不符合则往后遍历,直到找到符合的。(完整题目附在了最后) 代码如下: class Solution(object):def wiggleMaxLength(self, nums):…...
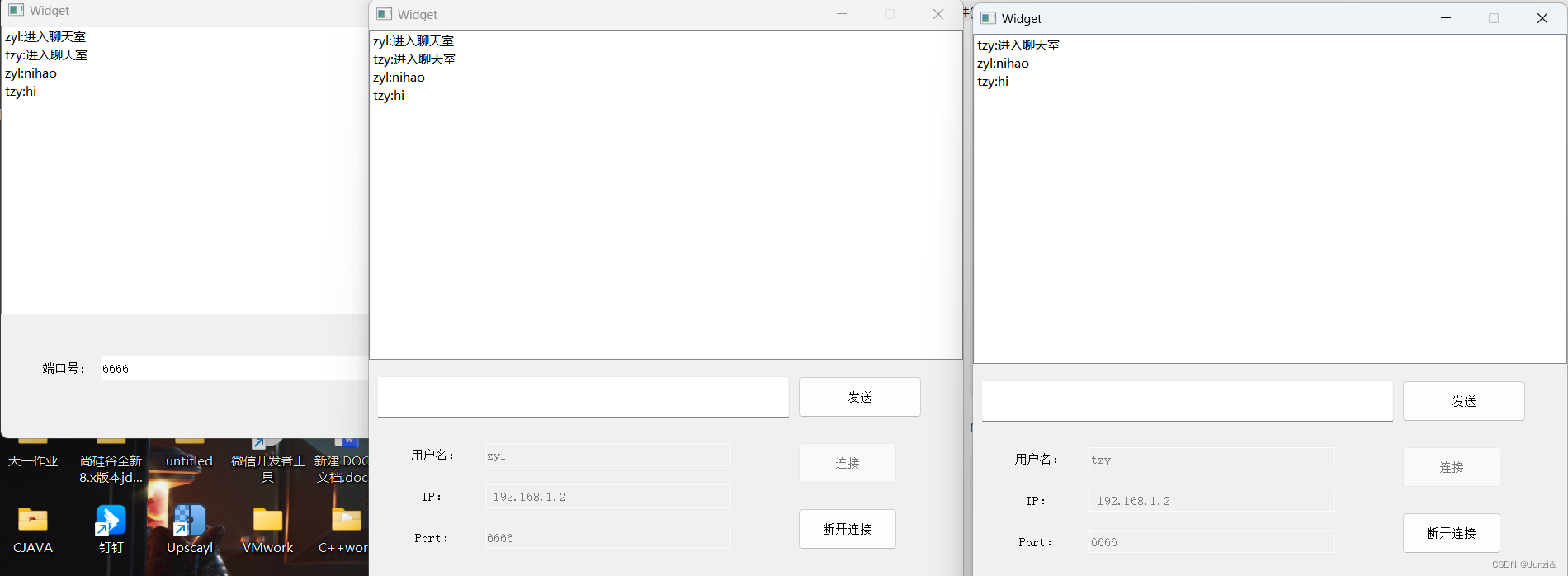
复习 --- QT服务器客户端
服务器: 头文件: #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include<QTcpServer> #include<QTcpSocket> #include<QMessageBox> #include<QDebug> #include<QList> #include<QListWidget> #in…...

Godot 官方2D游戏笔记(1):导入动画资源和添加节点
前言 Godot 官方给了我们2D游戏和3D游戏的案例,不过如果是独立开发者只用考虑2D游戏就可以了,因为2D游戏纯粹,我们只需要关注游戏的玩法即可。2D游戏的美术素材简单,交互逻辑简单,我们可以把更多的时间放在游戏的玩法…...

leetcode 热题 100
数组和字符串匹配 子串和子序列 原串:“abcabc” 子串:“abc”, 连续但不大于原串的字符串 子序列:“acc”, 字符来自原串且保持在原串中顺序不变的字符串 子排列: “aabbcc”, 字符来自原串且只能用1次,但可有不同排列顺序的字…...

Ae 效果:CC Lens
扭曲/CC Lens Distort/CC Lens CC Lens (CC 镜头)主要用于添加或移除摄像机镜头扭曲,比如桶形失真 Barrel、枕形失真 Pincushion以及鱼眼失真 Fisheye等。或者,用它来创建一些特殊的动画效果。 ◆ ◆ ◆ 效果属性说明 Center 中…...
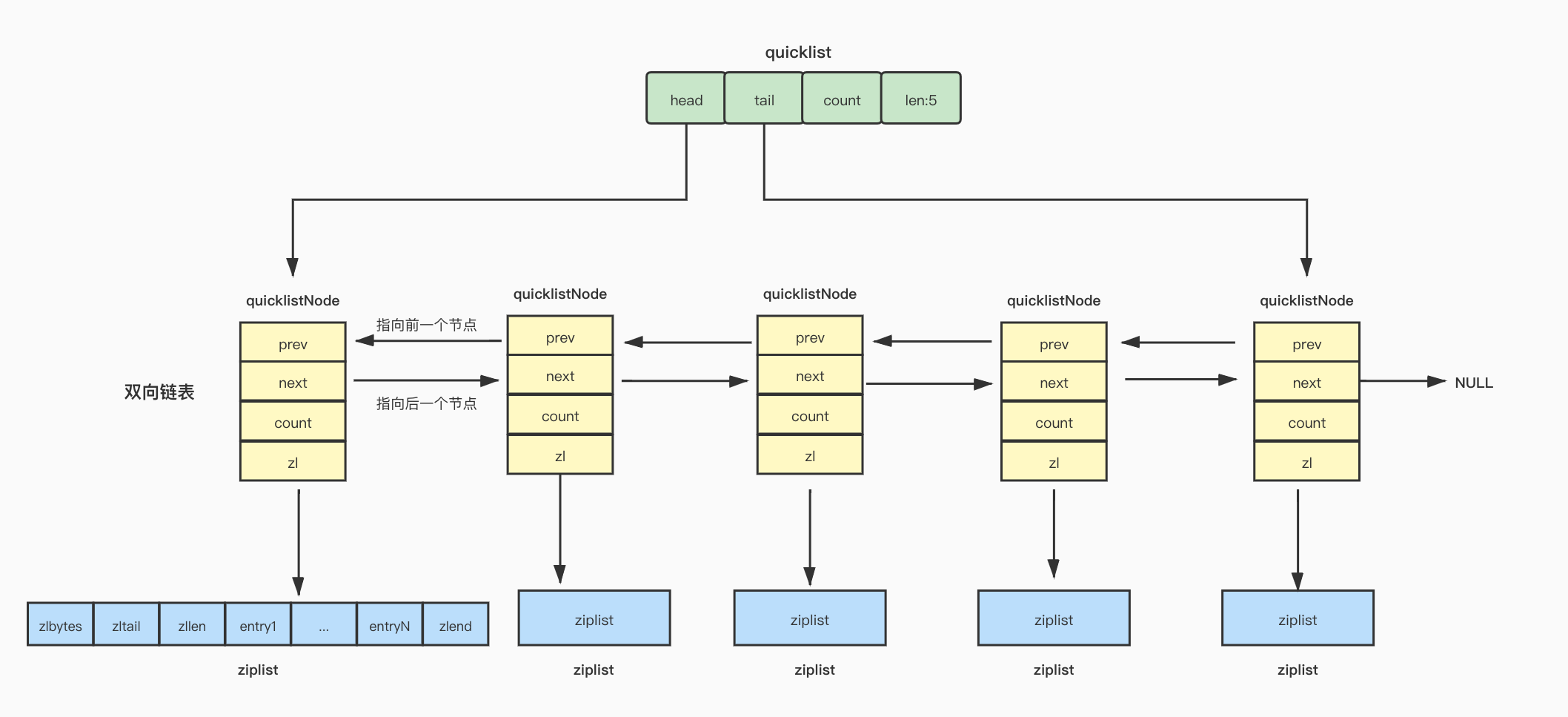
【Redis】基础数据结构-quicklist
Redis List 在Redis3.2版之前,Redis使用压缩列表和双向链表作为List的底层实现。当元素个数比较少并且元素长度比较小时,Redis使用压缩列表实现,否则Redis使用双向链表实现。 ziplist存在问题 不能保存过多的元素,否则查找复杂度…...

QT 实现服务器客户端搭建
1. 服务器头文件 #ifndef SER_H #define SER_H#include <QWidget> #include<QTcpServer> //服务器头文件 #include<QTcpSocket> //客户端头文件 #include<QMessageBox> //消息对话框 #include<QList> //链表头文件QT_BEGIN_NAM…...
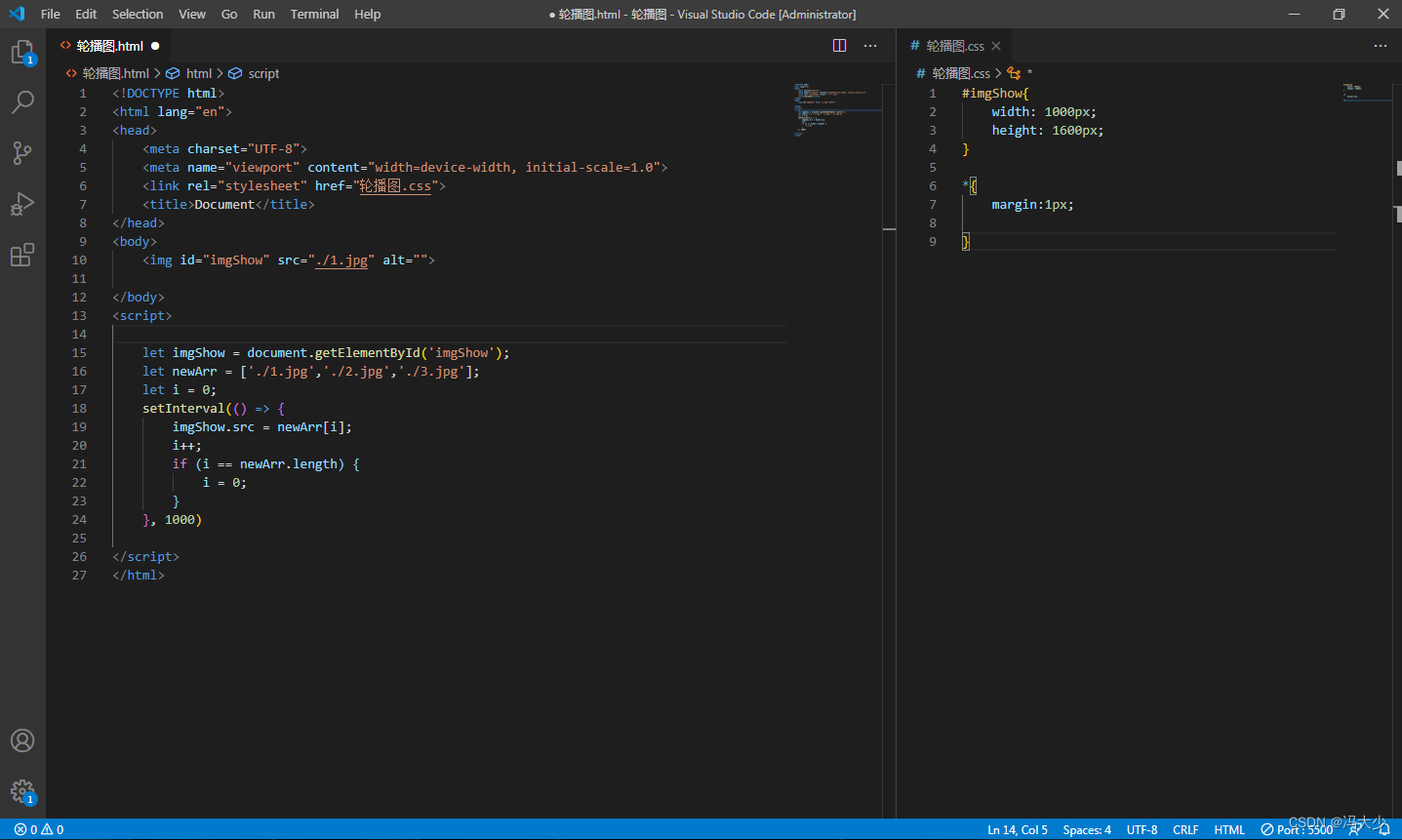
Javascript - 轮播图
轮播图也称banner图、广告图、焦点图、滑片。是指在一个模块或者窗口,通过鼠标点击或手指滑动后,可以看到多张图片。这些图片统称为轮播图,这个模块叫做轮播模块。可以通过运用 javascript去实现定时自动转换图片。以下通过一个小Demo演示如何运用Javascript实现。 <!DOCTYP…...

MATLAB中syms函数使用
目录 语法 说明 示例 创建符号标量变量 创建符号标量变量的向量 创建符号标量变量矩阵 管理符号标量变量的假设 创建和评估符号函数 syms函数的作用是创建符号标量和函数,以及矩阵变量和函数。 语法 syms var1 ... varN syms var1 ... varN [n1 ... nM] …...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
