Leetcode 1492.n的第k个因子

给你两个正整数 n 和 k 。
如果正整数 i 满足 n % i == 0 ,那么我们就说正整数 i 是整数 n 的因子。
考虑整数 n 的所有因子,将它们 升序排列 。请你返回第 k 个因子。如果 n 的因子数少于 k ,请你返回 -1 。
示例 1:
输入:n = 12, k = 3 输出:3 解释:因子列表包括 [1, 2, 3, 4, 6, 12],第 3 个因子是 3 。
示例 2:
输入:n = 7, k = 2 输出:7 解释:因子列表包括 [1, 7] ,第 2 个因子是 7 。
示例 3:
输入:n = 4, k = 4 输出:-1 解释:因子列表包括 [1, 2, 4] ,只有 3 个因子,所以我们应该返回 -1 。
提示:
1 <= k <= n <= 1000
进阶:
你可以设计时间复杂度小于 O(n) 的算法来解决此问题吗?
一、信息
1.给我两个整数n和k.
2.因子的定义
3.首先获取所有因子然后升序排列,返回第k个因子如果n小于k返回-1
二、分析
条件1.告诉我函数参数的类型
条件2.告诉我因子的定义
条件3.目的
三、步骤
第一步 获取两个整型变量 n和k
第二步 我们直接循环遍历用i来模拟除数然后循环取余找到所有的能整除N的i它们其实就是N的因子。问题出现用什么装这些数呢?我们用数组来存就行了方便索引
第三步 输入k 判断k的范围然后选择对应的路如果K<=n那么就直接按照数组索引就行了,如果大于返回-1.
步骤图:

四、问题出现
五、实现
错误代码:
C语言:
int kthFactor(int N,int k){int i,a[1000],sign=0;for(i=0;i<=N;i++){if(N%(i+1)==0){a[i]=i+1;sign++;}}if(k<sign){return printf("%d",a[k]);}else{return -1;}
}错误原因:
我的代码思路是基本正确的,但是有几个问题。
1. 数组`a`应该只存储n的因子。在你的代码中,由于使用`a[i]`来存储因子,这可能导致数组的不连续性,即有的数组位置是空的。
2. 当判断`if(k<sign)`时,应该是`k <= sign`。因为如果`k`正好等于因子的数量,那么仍然有一个有效的答案。
3. 当返回结果时,我使用`printf`,但题目要求的是返回整数值。所以我应该直接返回整数而不是打印它。
下面是修改后的代码:
int kthFactor(int N, int k) {int i, a[1000], sign = 0;for (i = 1; i <= N; i++) { // 从1开始遍历到Nif (N % i == 0) {a[sign] = i; // 存储因子到数组a中的连续位置sign++;}}if (k <= sign) { // k应该小于等于因子的数量return a[k - 1]; // 注意,因为数组是从0开始的,所以返回的应该是a[k-1]} else {return -1;}
}这样,我的函数能够正确返回第k个因子,在因子数量少于k时返回-1。
六、标准答案
大师的答案:
C语言:
#include <stdio.h>int kthFactor(int n, int k) {int count = 0; // 用来记录已经找到的因子的数量for (int i = 1; i <= n; i++) {if (n % i == 0) { // 判断i是否为n的因子count++;if (count == k) { // 如果已经找到k个因子,则返回当前的因子return i;}}}return -1; // 如果遍历完所有数字后还没有找到k个因子,则返回-1
}int main() {printf("%d\n", kthFactor(12, 3)); // 3printf("%d\n", kthFactor(7, 2)); // 7printf("%d\n", kthFactor(4, 4)); // -1return 0;
}
改正后我的答案:
C语言:
int kthFactor(int N, int k) {int i, a[1000], sign = 0;for (i = 1; i <= N; i++) { // 从1开始遍历到Nif (N % i == 0) {a[sign] = i; // 存储因子到数组a中的连续位置sign++;}}if (k <= sign) { // k应该小于等于因子的数量return a[k - 1]; // 注意,因为数组是从0开始的,所以返回的应该是a[k-1]} else {return -1;}
}
英雄师傅答案:
C语言版本:
int kthFactor(int n,int k){int i;int cnt=0;for(i=1;i<=n;i++){if(n%i==0){++cnt;if(cnt==k){return i;}}}return -1;
}大师的进阶答案:
是的,可以设计一个时间复杂度低于 \(O(n)\) 的算法来解决这个问题。一个更高效的方法是只需要遍历到![]() 。这是因为n的因子必定是成对出现的(例如,对于n=28,其因子包括1和28、2和14、4和7)。因此,只需遍历到
。这是因为n的因子必定是成对出现的(例如,对于n=28,其因子包括1和28、2和14、4和7)。因此,只需遍历到 ![]() ,对于每个找到的因子i,我们可以同时找到另一个因子
,对于每个找到的因子i,我们可以同时找到另一个因子 ![]() 。
。
以下是根据这个思路修改的代码:(这个答案是错的正确的在下面)
int kthFactor(int n, int k) {int count = 0;for (int i = 1; i * i <= n; i++) {if (n % i == 0) {count++;if (count == k) {return i;}if (i != n / i) { // 避免重复计数,例如n=4时,只有一个因子2count++;}if (count == k) {return n / i;}}}return -1;
}
问题1:不知道你是否会疑问为什么找一个数的因子的时候找到根号下n就可以了,因此我会对这一结论进行证明:
证明问题1:
首先我们要引入一个数学中新的概念——因子配对特性
"因子配对"特性是指当你找到一个数 \(n\) 的因子时,你实际上同时找到了两个因子(除非 \(n\) 是一个完全平方数),这两个因子在乘法上互为倒数。
具体来说,如果 \(a\) 是 \(n\) 的一个因子,并且 \(a \leq \sqrt{n}\),那么必定存在另一个因子 \(b\),它是 \(n\) 除以 \(a\) 的结果,即 \(b = \frac{n}{a}\),并且 \(b \geq \sqrt{n}\)。
这两个因子 \(a\) 和 \(b\) 形成一个配对,因为它们都可以乘以对方得到 \(n\):\(a \times b = n\)。
举例来说,对于 \(n = 28\):
- \(1\) 是一个因子,它的配对因子是 \(28/1 = 28\)。
- \(2\) 是一个因子,它的配对因子是 \(28/2 = 14\)。
- \(4\) 是一个因子,它的配对因子是 \(28/4 = 7\)。
这里的关键观察是,如果 \(n\) 不是一个完全平方数,那么只有在 \(a = \sqrt{n}\) 时,因子 \(a\) 和 \(b\) 才会相同。在所有其他情况下,因子 \(a\) 和 \(b\) 都会不同。因此,只需要检查到 \(\sqrt{n}\) 就足够了,因为这样可以确保你找到 \(n\) 的所有因子。
好接下来是证明部分:
证明:
要证明为什么找因子只需要检查到 \(\sqrt{n}\),我们可以从因子的配对特性入手。
**证明**:
1. 假设 \(d\) 是 \(n\) 的一个因子,那么存在整数 \(e\) 使得 \(d \times e = n\)。
2. 假设两者都大于 \(\sqrt{n}\),即 \(d > \sqrt{n}\) 且 \(e > \sqrt{n}\)。那么它们的乘积 \(d \times e\) 会大于 \(n\)(因为 \(d \times e > \sqrt{n} \times \sqrt{n} = n\)),这与我们的假设 \(d \times e = n\) 矛盾。
3. 同样,如果两者都小于 \(\sqrt{n}\),那么它们的乘积 \(d \times e\) 会小于 \(n\)。
4. 因此,其中一个因子(如 \(d\))必然小于或等于 \(\sqrt{n}\),而另一个因子(如 \(e\))则必然大于或等于 \(\sqrt{n}\)。
5. 这意味着,为了找到 \(n\) 的所有因子,我们只需要检查小于或等于 \(\sqrt{n}\) 的数。对于每个找到的因子 \(d\),我们可以得到另一个配对的因子 \(e = n/d\)。
综上所述,为了找到一个数的所有因子,只需要检查到该数的平方根即可。
但是大师这道题目做错了——哈哈哈
正确答案:
#include <math.h> // 为了使用 sqrt 函数int kthFactor(int n, int k) {int count = 0, factor;for (factor = 1; factor * factor <= n; ++factor) {if (n % factor == 0) {++count;if (count == k) {return factor;}}}--factor;if (factor * factor == n) {--factor;}for (; factor > 0; --factor) {if (n % factor == 0) {++count;if (count == k) {return n / factor;}}}return -1;
}
有谁知道为什么吗?
问题在于如何处理找到的因子,尤其是当考虑完全平方数时。
在我的最初答案中,我尝试在第一个循环内部直接找到并返回第k个因子。但这种方法在处理大于 \(\sqrt{n}\) 的因子时出现了问题,因为我没有再次从 \(\sqrt{n}\) 开始向下遍历来找到这些因子。
而你提供的答案则修复了这个问题。首先,它遍历到 \(\sqrt{n}\) 来找到小于或等于 \(\sqrt{n}\) 的因子。如果n是完全平方数(例如,n = 36,那么 \(\sqrt{n} = 6\)),它会减少因子值以避免下一个循环中的重复。然后从 \(\sqrt{n}\) 开始向下遍历,这样就可以适当地计数并找到大于 \(\sqrt{n}\) 的因子。
我的错误在于没有正确处理和计数大于 \(\sqrt{n}\) 的因子,这导致了答案的不准确性。
Leetcode官方题解
C++:
class Solution { public:int kthFactor(int n, int k) {int count = 0, factor;for (factor = 1; factor * factor <= n; ++factor) {if (n % factor == 0) {++count;if (count == k) {return factor;}}}--factor;if (factor * factor == n) {--factor;}for (; factor > 0; --factor) {if (n % factor == 0) {++count;if (count == k) {return n / factor;}}}return -1;} };
总结:
学到了什么
从这道题目和相应的解答中,我们可以学到多个方面的知识和技巧:
1. **因子配对特性**:任何大于 \(\sqrt{n}\) 的因子必定与小于 \(\sqrt{n}\) 的一个因子配对。利用这个特性,我们可以大大减少搜索范围,从而优化算法。
2. **完全平方数的处理**:当 \(n\) 是一个完全平方数时,其平方根只能计为一个因子,而不是两个。这是一个细节,但在某些情况下可能会导致错误,因此需要注意。
3. **复杂度的重要性**:通过观察问题的数学属性,我们可以设计更高效的算法。在这种情况下,我们将时间复杂度从 O(n) 降低到 O(\(\sqrt{n}\))。
4. **代码审查和验证**:即使在听起来正确的逻辑下,代码也可能存在错误或遗漏。对代码进行细致的审查,并在多种测试用例下验证它的正确性,是非常重要的。
5. **问题解决的迭代过程**:我们首先尝试一个直接的解决方案(遍历所有可能的因子),然后基于观察和数学知识进一步优化。这种迭代的方法在算法和编程中是很常见的。
6. **边界条件的重要性**:在算法和编程中,很容易忽视边界条件或特殊情况(例如,当 \(n\) 是完全平方数时)。对这些情况进行特别处理通常是正确性的关键。
总的来说,这道题目不仅测试了我们的编程能力,还测试了我们的数学知识、观察力和问题解决能力。
犯了什么错
从此问题和之前的答案中,我们可以分析以下几点:
1. **对数学性质的不足理解**:最开始没有充分利用数学上的因子配对特性,这导致解法不够优化。对基本的数学概念和性质有深入的了解和直觉可以帮助我们更快地识别并解决这类问题。
2. **细节处理不够精确**:在处理完全平方数时,出现了细节处理上的疏忽。编程题常常考察细节处理能力,这需要我们对问题有全面和深入的理解。
3. **测试和验证的不足**:如果我们对初步的解决方案进行了更广泛和深入的测试,可能早期就发现了问题。有系统地测试各种边界情况和特殊输入的习惯是非常重要的。
4. **反思和修正的重要性**:当被指出有错误时,及时地检查、反思并修正是非常必要的。这不仅帮助我们找到正确的解决方案,还能帮助我们从错误中学习。
错误是学习的一部分,关键是我们如何从中学习和成长。通过识别并分析我们的错误,我们可以更好地知道自己的弱点,从而针对性地进行改进。

相关文章:

Leetcode 1492.n的第k个因子
给你两个正整数 n 和 k 。 如果正整数 i 满足 n % i 0 ,那么我们就说正整数 i 是整数 n 的因子。 考虑整数 n 的所有因子,将它们 升序排列 。请你返回第 k 个因子。如果 n 的因子数少于 k ,请你返回 -1 。 示例 1: 输入&#…...
十一工具箱流量主小程序源码
无授权,去过滤机制版本 看到网上发布的都是要授权的 朋友叫我把他去授权,能用就行 就把过滤去了 这样就不用授权 可以免费使用 白嫖党专属 一切接口可用,无需担心不能用 授权者不关站一直可以用 源码下载:https://download.csdn.…...
10.5汇编语言整理
【汇编语言相关语法】 1.汇编语言的组成部分 1.伪操作:不参与程序的执行,但是用于告诉编译器程序该怎么编译 .text .global .end .if .else .endif .data 2.汇编指令 编译器将一条汇编指令编译成一条机器码,在内存里一条指令占4字节内存&…...

Connect to 127.0.0.1:1080 [/127.0.0.1] failed: Connection refused: connect
报错信息 A problem occurred configuring root project CourseSelection. > Could not resolve all artifacts for configuration :classpath.> Could not resolve com.android.tools.build:gradle:3.6.1.Required by:project :> Could not resolve com.android.tool…...
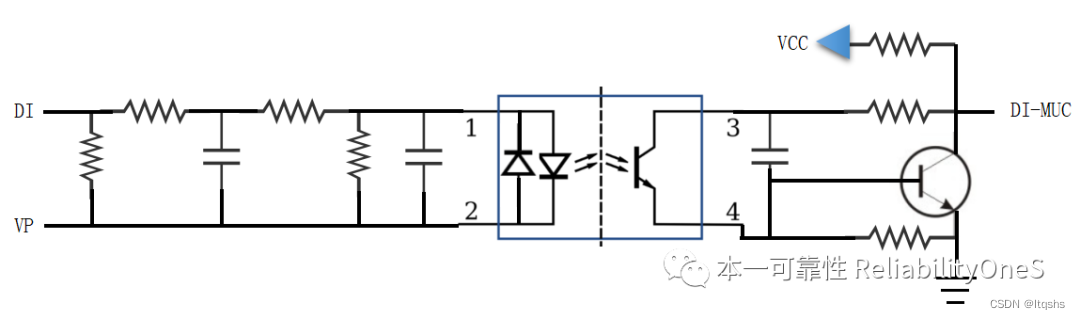
驱动器类产品的接口EMC拓扑方案
驱动器类产品的接口EMC拓扑方案 1. 概述 本文以高压伺服驱动器和变频器类产品为例,对常用端口滤波拓扑方案进行总结,后续根据不同的应用场景可进行适当删减,希望对大家有帮助。 2. 驱动器验证等级 本文推荐拓扑的实验结果,满足…...
2023最新ICP备案查询系统源码 附教程 Thinkphp框架
2023最新ICP备案查询系统源码 附教程 thinkphp框架 本系统支持网址备案,小程序备案,APP备案查询,快应用备案查询 优势: 响应速度快,没有延迟,没有缓存,数据与官方同步 源码下载:ht…...

大数据Doris(六):编译 Doris遇到的问题
文章目录 编译 Doris遇到的问题 一、js_generator.cc:(.text+0xfc3c): undefined reference to `well_known_types_js’...
vue重修004上部
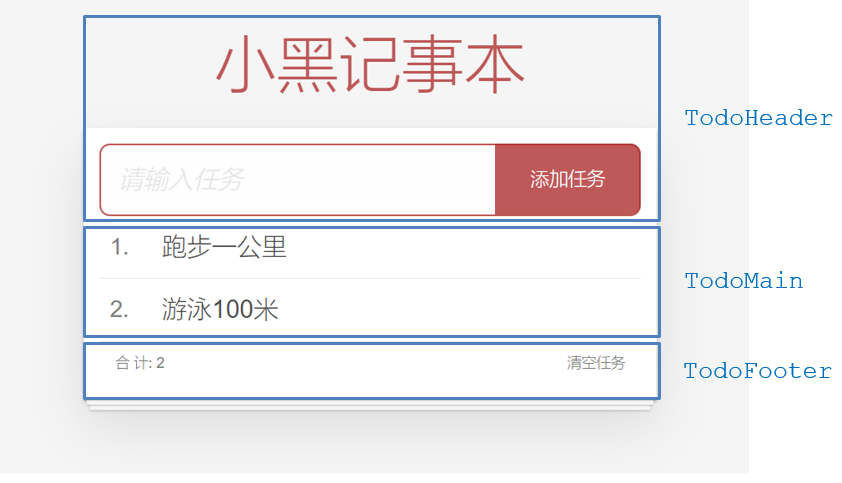
文章目录 版权声明组件的三大组成部分scoped解决样式冲突scoped原理2.代码演示 组件data函数说明演示 组件通信组件关系分类通信解决方案父子通信流程子向父通信代 props详解props校验props&data、单向数据流 小黑记事本(组件版)基础组件结构需求和实…...

【C++ techniques】要求/禁止/判断—对象产生于堆中
有时候我们想让某种对象具有“自杀”的能力,所以我们必须要求对象存在堆中,以便我们调用delete this;另一些时候,我们要求拥有某种确定性,保证某一些类型绝不会发生内存泄漏,原因是没有任何一个该类型的对象…...

吃鸡高手亲授:玩转绝地求生,分享顶级游戏干货!
绝地求生(PUBG)自上线以来,成为了全球热门游戏。作为吃鸡行家,我将分享一些独家技巧和干货,帮助您提高游戏战斗力,享受顶级游戏作战体验! 首先,让我们谈一谈战斗力升级。想要在吃鸡游…...

Vue中如何进行自定义图表与可视化图形设计
Vue中如何进行自定义图表与可视化图形设计 在现代Web应用程序开发中,数据可视化图表和图形设计是至关重要的一部分。Vue.js是一个流行的JavaScript框架,它提供了强大的工具来构建交互性强大的用户界面。本文将探讨如何在Vue.js中进行自定义图表和可视化…...
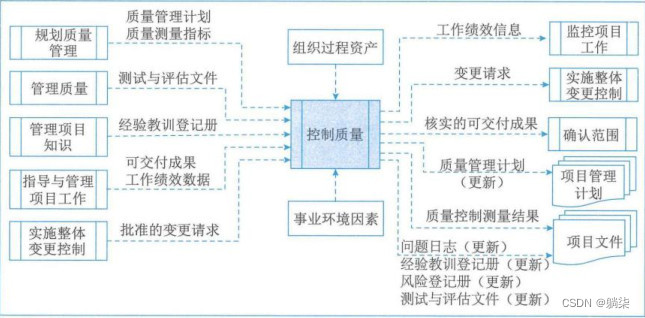
学信息系统项目管理师第4版系列19_质量管理
1. 公差 1.1. 质量测量中公差是测量指标的可允许变动范围,而不是实际测量值与预期值的差 1.1.1. 【高22下选35】 1.2. 结果的的可接受范围 2. 控制界限 2.1. 统计意义上稳定的过程或过程绩效的普通偏差的边界 3. 3版 3.1. 质量控制新七工具 3.1.1. 【高19下…...

react库的基础学习
React介绍 React.js是前端三大新框架:Angular.js、React.js、Vue.js之一,这三大新框架的很多理念是相同的,但是也有各自的特点。 React起源于Facebook的内部项目,因为该公司对市场上所有 JavaScript MVC 框架,都不满…...
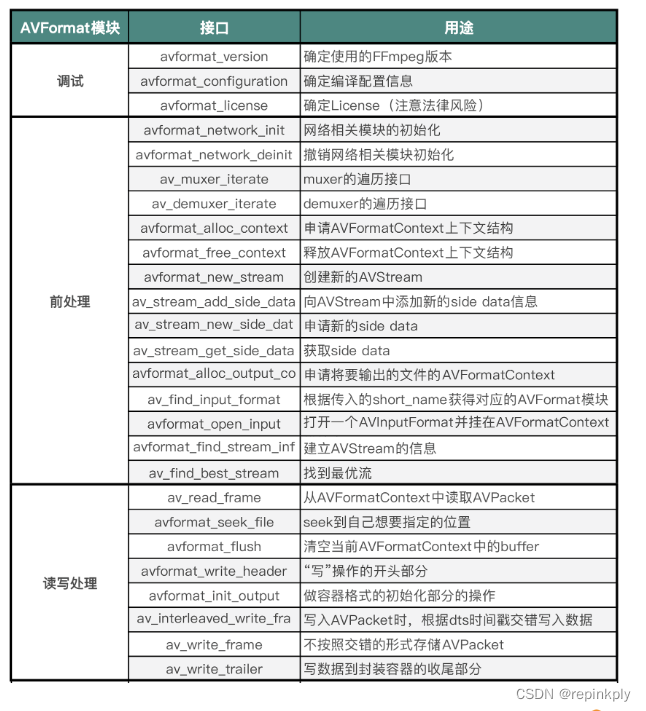
FFmpeg 基础模块:容器相关的 API 操作
目录 AVFormat 模块 AVFormat 前处理部分 AVFormat 读写处理部分 小结 思考 FFmpeg 目录中包含了 FFmpeg 库代码目录、构建工程目录、自测子系统目录等,具体内容如下: 现在你知道 FFmpeg 的源代码目录中都包含了哪些内容,在之后使用 FFm…...
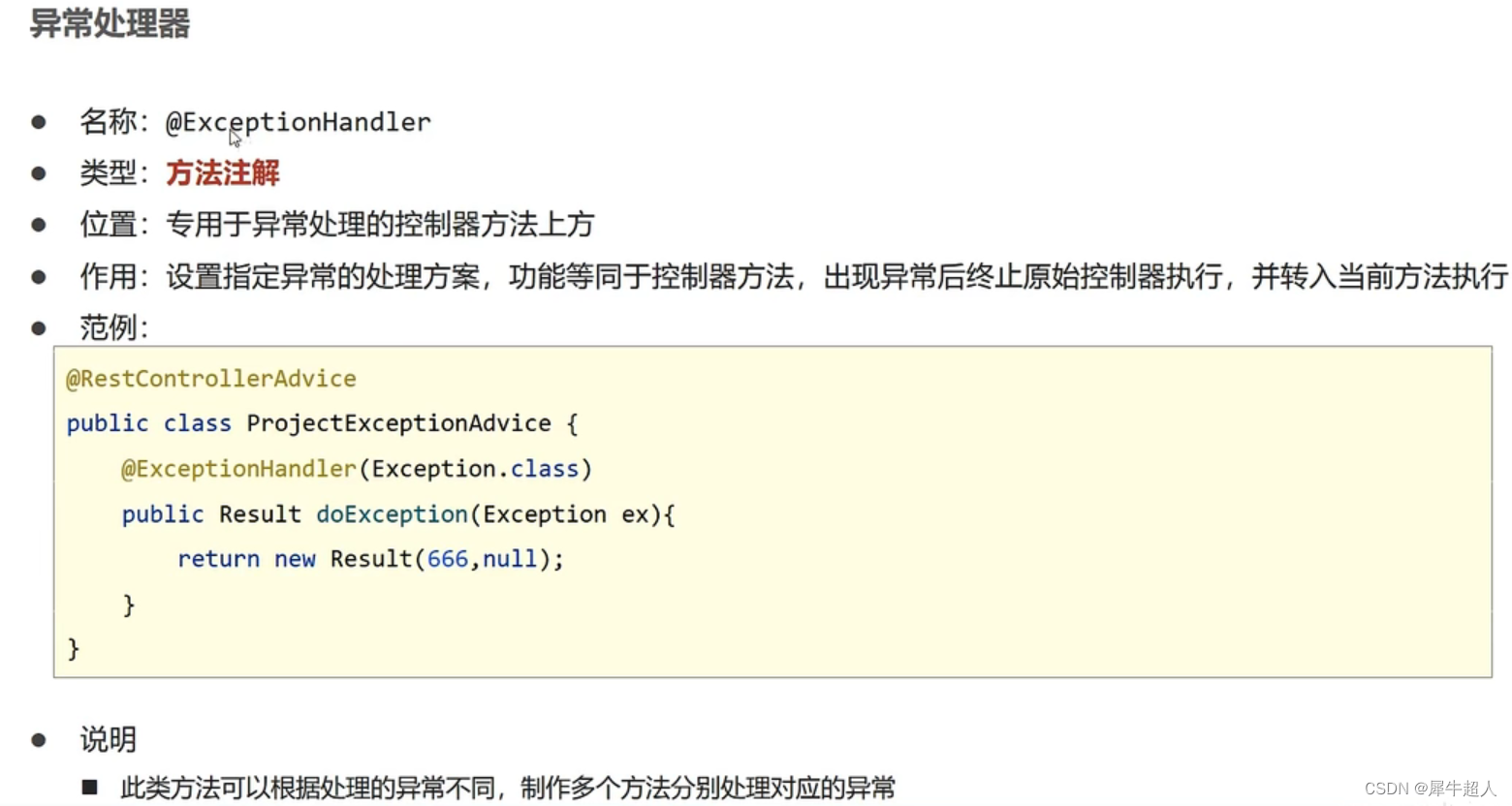
SpringMVC+统一表现层返回值+异常处理器
一、统一表现层返回值 根据我们不同的处理方法,返回的数据格式都会不同,例如添加只返回true|false,删除同理,而查询却返回数据。 Result类 为此我们封装一个result类来用于表现层的返回。 public class Result {//描述统一格式…...
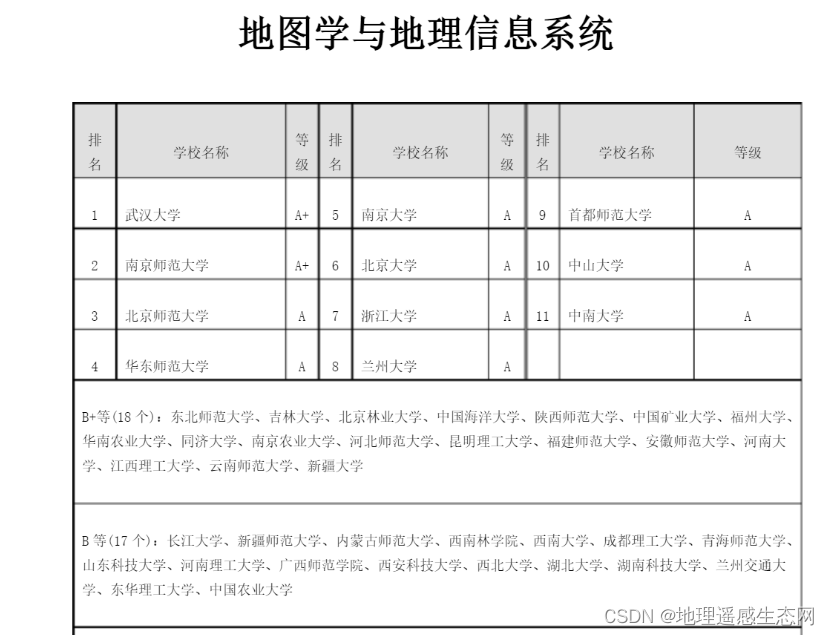
2023年地理信息系统与遥感专业就业前景与升学高校排名选择
活动地址:毕业季进击的技术er 地理信息系统(GIS,Geographic Information System),又称“地理信息科学”(Geographic Information Science),是一种具有信息系统空间专业形式的数据管理…...
的语法))
第五章:最新版零基础学习 PYTHON 教程—Python 字符串操作指南(第二节 - Python 字符串—Python 字符串 len()的语法)
Python len() 函数返回字符串的长度。 目录 Python len() 语法 Python len() 示例 示例 1:带有元组和字符串的 Len() 函数...
ubuntu22.04使用共享文件设置
从ubuntu20.04开始,设置共享文件就很麻烦 第一步: 安装samba: sudo apt install samba第二步; 创建一个共享文件夹 我以桌面Desktop为例子 第三步: 设置密码: sudo smbpasswd -a ygc第四步: sudo vim …...

pycharm配置python3.8版本专门用于undecteded_chromedriver测试
pycharm配置python3.8版本专门用于undecteded_chromedriver测试 作者:虚坏叔叔 博客:https://pay.xuhss.com 早餐店不会开到晚上,想吃的人早就来了!😄 一、Pycharm及python环境的配置 1.安装python-3.8.7rc1-amd64.e…...
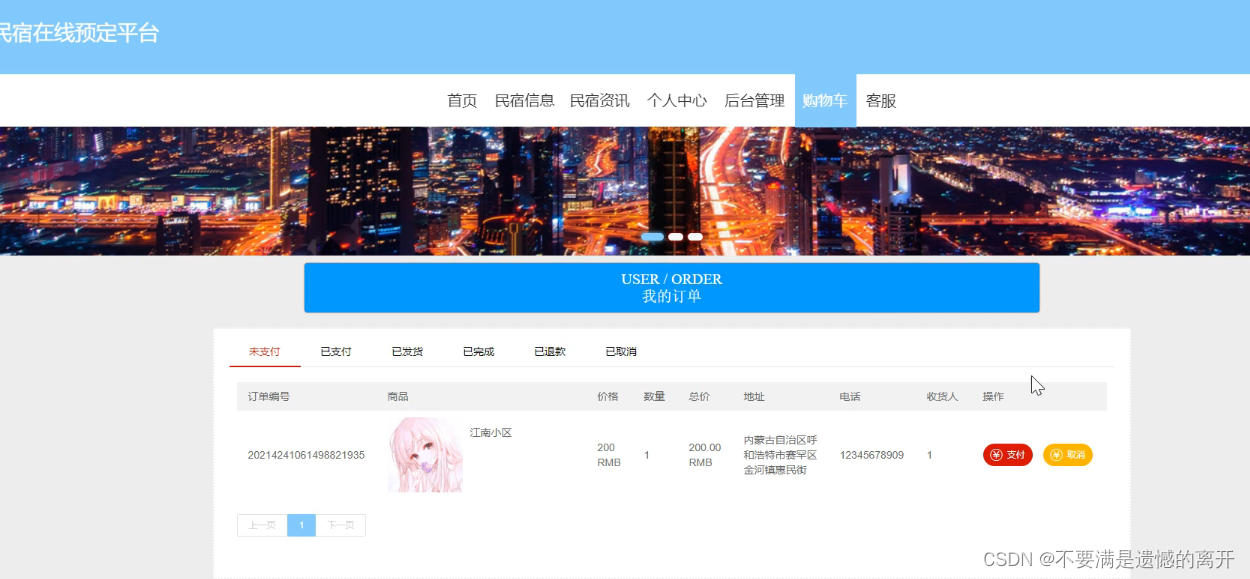
基于SpringBoot的民宿在线预定平台
目录 前言 一、技术栈 二、系统功能介绍 用户信息管理 民宿信息管理 民宿资讯管理 民宿分类管理 用户注册 民宿信息 我的订单 三、核心代码 1、登录模块 2、文件上传模块 3、代码封装 前言 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

