数据结构——AVL树(详解 + C++模拟实现)
文章目录
- 前言
- AVL树的概念
- AVL树节点的定义
- AVL树类框架
- AVL树的插入
- AVL树的旋转
- 新节点插入较高子树的左侧 —— 左左: 右单旋
- 新节点插入较高右子树的右侧——右右: 左单旋
- 新节点插入较高左子树的右侧 —— 左右: 先左单旋然后再有单旋
- 新节点插入较高右子树的左侧:右左单旋
- 旋转总结
- AVL树插入完整代码
- AVL树的验证
- 验证其为二叉搜索树
- 验证其为平衡树
- AVL树的删除
- AVL树的性能
- 完整实现代码
- 总结
前言
本篇博客将为大家详细讲述AVL树是什么以及其相对于普通的二叉搜索树有什么优点,将详细讲述其拥有哪些性质,并且通过模拟实现的方式让大家对该数据结构有更深入的理解和认识,对于该数据结构的增删查改操作,其中的删除操作是在普通搜索二叉树的基础上进行一些改进,会简单提及,但不会细讲,重点将会讲述插入操作,查和改操作和二叉搜索树一模一样,也不做讲解。
由于AVL树是一棵特殊的二叉搜索树,因此想要学习AVL树需要先知道二叉搜索树是什么东西,如果有不知道二叉搜索树是什么的小伙半可以先看看博主的另一篇博客:
数据结构—— 二叉搜索树(附c++模拟实现)
该篇博客详细介绍了二叉搜索树。
AVL树的概念
我们知道,二叉搜索树虽然可以缩短查找的效率,但如果数据有序或接近有序,那么此时二叉搜索树将会退化成单支树,此时的查找效率和在链表中搜索等同,效率低下,因此,两位俄罗斯的数学家(G.M.Adelson-Velskii 和E.M.Landis)在1962年的时候发明了一种解决上述问题的方法:
当向二叉搜索树中插入新节点后,如果能够保证每个节点的左右子树高度差的绝对值不超过1(在不破坏二叉搜素树性质的情况下对树中节点进行调整),即可降低树的高度,从而减少平均搜索长度。
因此,AVL树就这样诞生了!
一棵AVL树可以是空树,或者是具有如下性质的搜索二叉树:
- 它的左右子树都是AVL树
- 左右子树高度之差的绝对值超过1
因此,对于一棵AVL树,最重要的就是如何控制每棵树左右子树高度之差都不超过1,这种控制是通过翻转操作来实现的,博主在下文会重点讲解。
另外,AVL树的实现方式有两种,一种就是在插入的过程中动态的检查左右子树的高度差是否超过1,另外一种就是引入一个新的概念——平衡因子,对于每个节点都存储一个int值表示该根节点左右子树的高度差,负数代表左子树更高,正数代表右子树更高,然后在插入的过程中不断维护每个节点的平衡因子即可。
这里由于第二种方法实现起来相对逻辑更加清晰,所以我们采用第二种方法进行模拟实现,并且用key_value的模型进行实现
AVL树节点的定义
和普通二叉搜索树节点定义不同的是,AVL树的节点为了方便进行旋转操作,需要多加一个指针指向其双亲节点,并且还要有一个int值表示平衡因子,定义如下:
template<typename K, typename V>
struct TreeNode
{pair<K, V> _kv;TreeNode<K, V>* _parent = nullptr;TreeNode<K, V>* _left = nullptr;TreeNode<K, V>* _right = nullptr;int _bf = 0; //balance factorTreeNode(const K& key, const V& value):_kv({ key, value }){}
};
AVL树类框架
template<typename K, typename V>
class AVL_Tree
{typedef TreeNode<K, V> node;
private:node* _root = nullptr;
public:bool insert(const pair<K, V>& kv) void inorder();void is_AVL();
};AVL树的插入
AVL树就是在二叉搜索树的基础上引入平衡因子,因此插入过程其实可以分成两步:
- 按照二叉搜索树的方式插入新节点
- 调整节点的平衡因子
对于第一步按照二叉搜索树的规则插入新节点的步骤这里不进行详解,这里重点讲解如何调整插入节点后各个AVL树节点的平衡因子。
pCur表示新插入的节点,pParent表示新插入节点的父节点,(需要找到父节点是节点定义时需要定义指向双亲的指针的原因之一)。
pCur插入后,pParent的平衡因子一定需要调整,插入之前,pParent的平衡因子分为三种情况(-1/0/1),而根据pCur插入位置的不同,可以分为以下两种情况:
- 如果
pCur插入到pParent的左侧,只需要给pParent的平衡因子减一- 如果
pCur插入到pParent的右侧,只需要给pParent的平衡因子加一
pParent的平衡因子经过修改后,可能会出现五种情况,0,±1,±2
- 如果
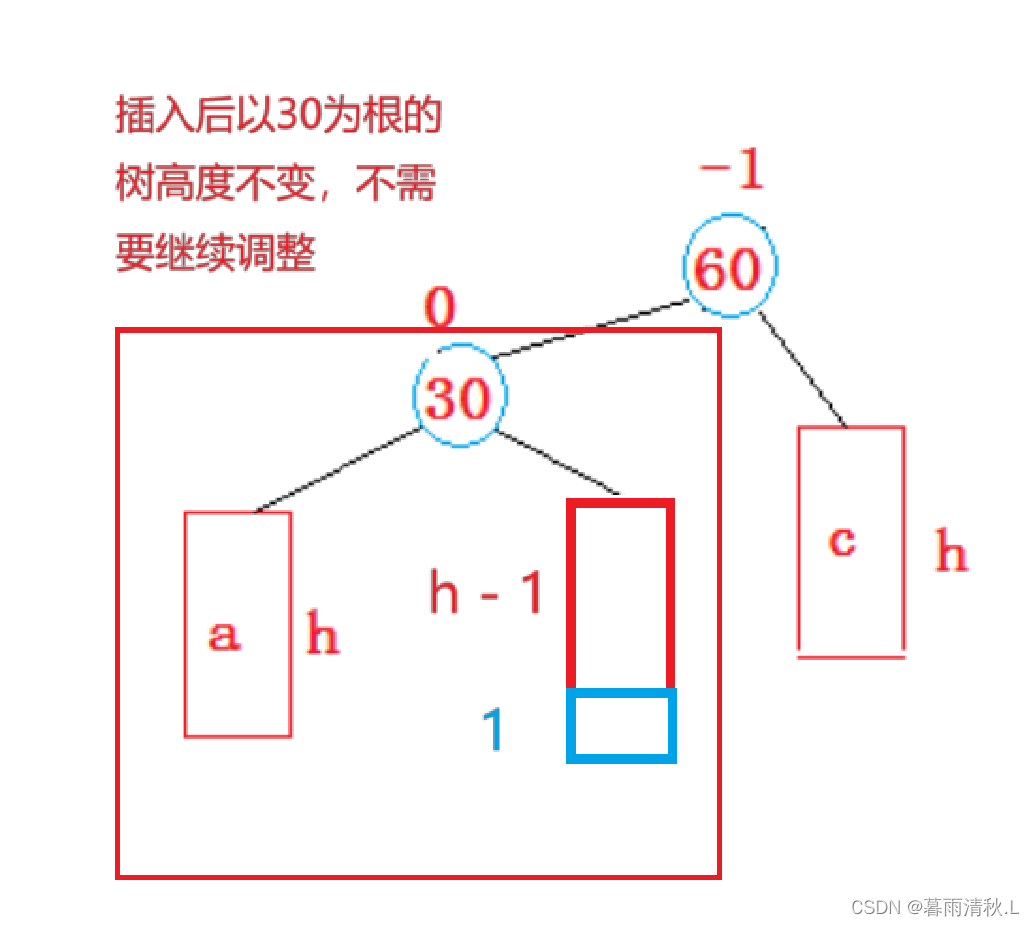
pParent的平衡因子为0,说明修改后以pParent为根节点的最高高度并没有发生变化,所以无需继续调整,插入成功
如下图所示:- 如果插入后
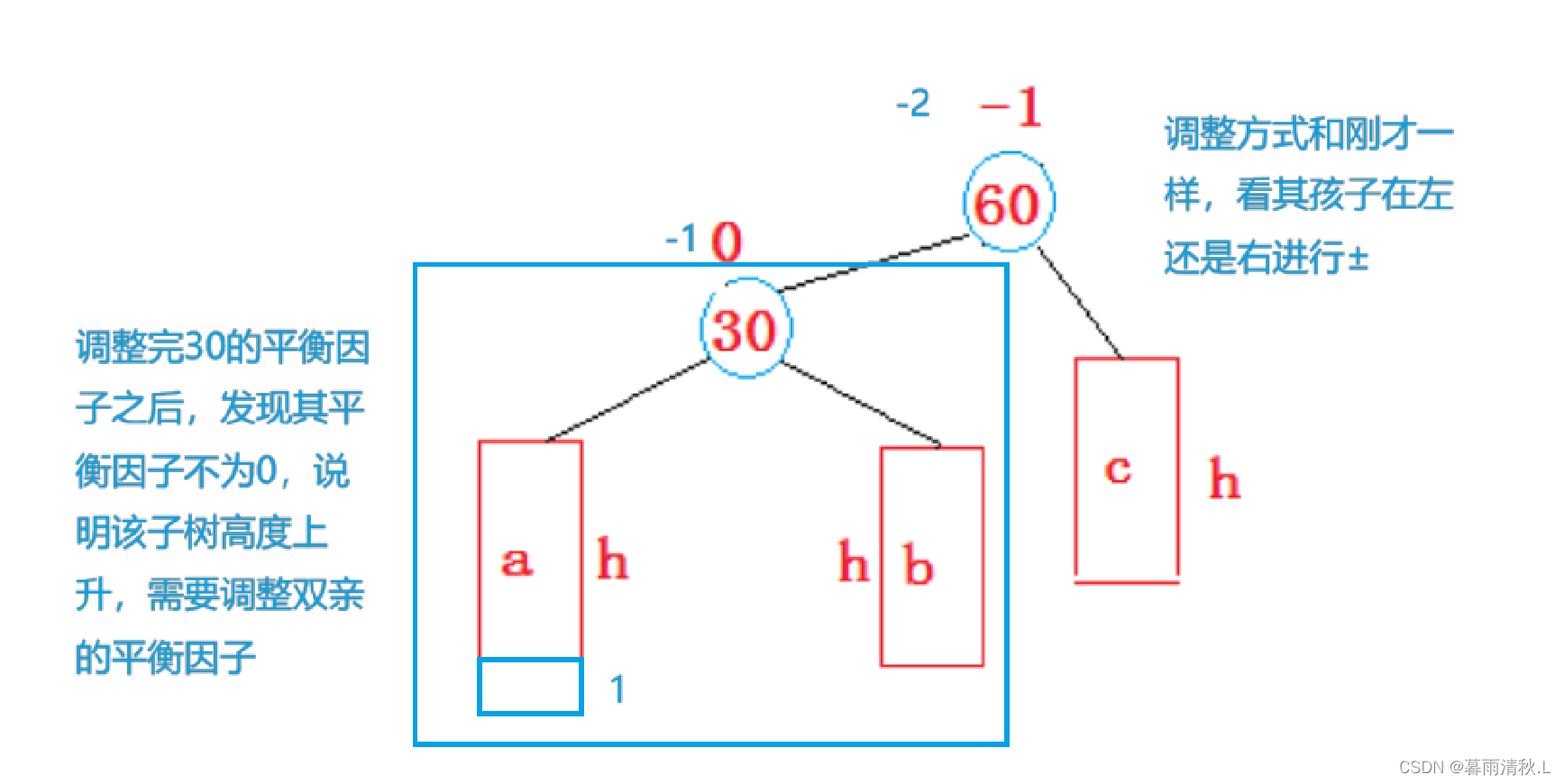
pParent的平衡因子为±1,说明插入前pParent的平衡因子一定是0,插入后被更新成±1,说明插入后以pParent为根的子树高度增加了1,也就是说我们需要继续向上更新祖先节点的平衡因子
如下图所示:
这个过程将不断循环,直到一直更新到pParent的平衡因子为0或者pParent更新到根节点为止。
- 如果
pParent的平衡因子为±2,那么此时以pParent为根的树已经不满足AVL树的性质了,此时,就需要进行旋转操作,对于旋转是什么,我们在下一个小节进行讲解,这里先给出插入代码整体框架:
bool insert(const pair<K, V>& kv){//如果头节点为空,直接将值赋给头节点即可if (!_root){node* newNode = new node(kv.first, kv.second);_root = newNode;return true;}//如果不为空,寻找插入位置node* parent = nullptr, *cur = _root;while (cur){auto& key = cur->_kv.first;parent = cur;if (kv.first > key)cur = cur->_right;else if (kv.first < key)cur = cur->_left;else return false;}node* newNode = new node(kv.first, kv.second);//循环结束,找到插入位置if (parent->_kv.first < kv.first)parent->_right = newNode;elseparent->_left = newNode;newNode->_parent = parent;cur = newNode;//更新平衡因子while (parent){//先修改因子//判断新增节点的方位对parent的平衡因子进行处理if (parent->_right == cur)parent->_bf++;elseparent->_bf--;if (parent->_bf == 0) break;//如果parent的平衡因子为±1,继续处理else if (abs(parent->_bf) == 1){cur = parent;parent = parent->_parent;}else if (abs(parent->_bf) == 2){//此时以pParent为根的子树已经违反了AVL树的特性,需要进行旋转处理//...}//由于平衡因子的情况只有以上五种,出现其他种类的平衡因子说明AVL树已经被破坏//通过抛异常来显示else throw "the bf out_of_range";}return true;}
AVL树的旋转
上一小节说到,在一棵本来是平衡的AVL树中插入一个新节点,可能导致不平衡,必须调整树的结构,使之平衡,这一步也叫做旋转,AVL树的旋转也分为四种:
旋转的本质其实是使高度较高的子树高度降低,然后将降低的高度给到其另一个较低的子树
新节点插入较高子树的左侧 —— 左左: 右单旋
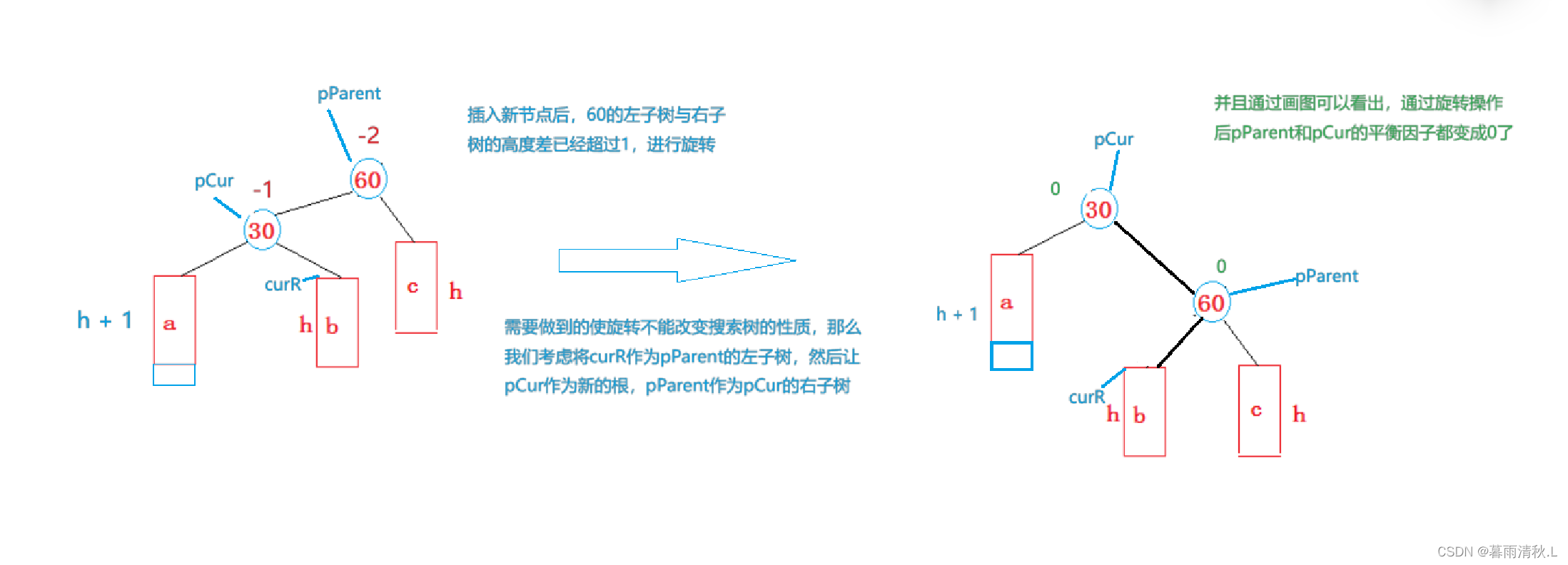
上图是左单旋的普遍思路,但是我们还需要考虑一些特殊场景:
- 30的右孩子可能存在,也可能不存在
- 60可能是根节点,也可能是子树
如果60是根节点,旋转完成之后需要更新根节点,如果60是子树,可能是左子树也可能是右子树,需要注意更改上面的链接关系
这里大家可以自行画图模拟一下各种特殊场景,至于为什么要考虑这些场景,是因为虽然整个思路很简单,但是由于我们整棵树是以三叉链的形式来存储的,所以修改过程中需要维护这一结构。
下面是右旋代码:
void reverseR(node* parent)
{node* cur = parent->_left, *ppnode = parent->_parent;node* curR = cur->_right;//连接parent和curRparent->_left = curR;if (curR)curR->_parent = parent;//连接cur和parentcur->_right = parent;parent->_parent = cur;//连接ppnode和curcur->_parent = ppnode;if (ppnode){if (ppnode->_right == parent)ppnode->_right = cur;elseppnode->_left = cur;}else_root = cur;//跟新bfparent->_bf = cur->_bf = 0;
}
新节点插入较高右子树的右侧——右右: 左单旋
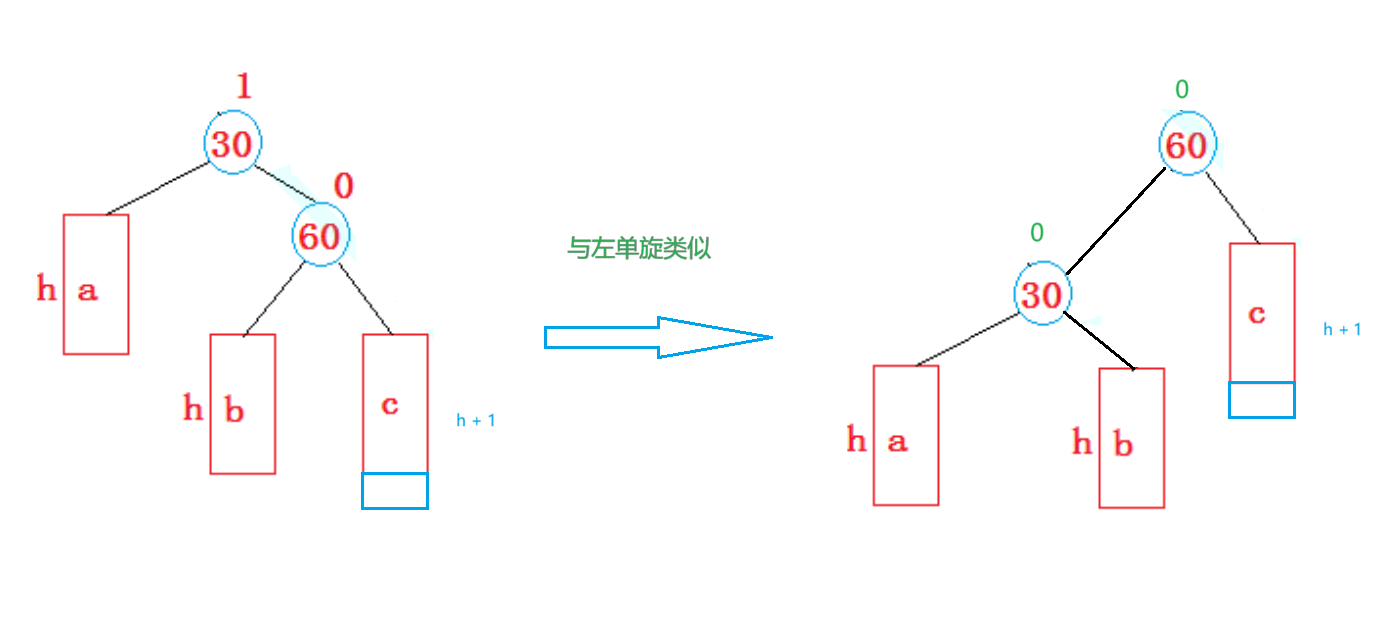
由于右单旋和左单旋基本类似,这里不进行细致讲解,下面是实现代码:
void reverseL(node* parent)
{node* ppnode = parent->_parent, *cur = parent->_right;node* curL = cur->_left;// 连接parent和curLeftparent->_right = curL;if (curL) curL->_parent = parent;// 连接parent和curcur->_left = parent;parent->_parent = cur;//跟新parent和cur的平衡因子parent->_bf = cur->_bf = 0;//更新根节点或者与ppnode的连接关系if (ppnode){if (ppnode->_right == parent)ppnode->_right = cur;elseppnode->_left = cur;cur->_parent = ppnode;}else{_root = cur;cur->_parent = nullptr;}
}
新节点插入较高左子树的右侧 —— 左右: 先左单旋然后再有单旋
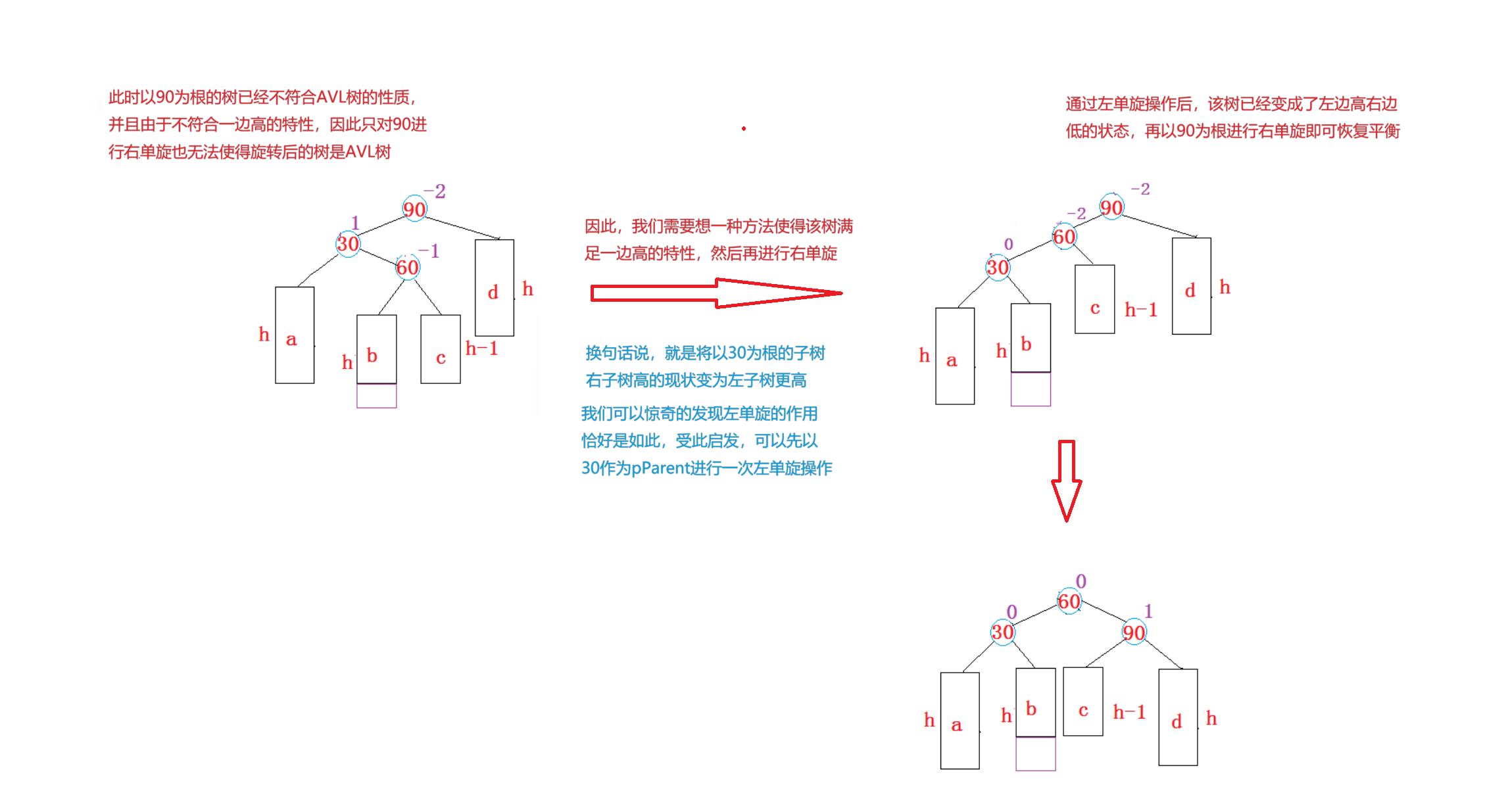
其次,对于右左单旋来说还有一个需要考虑的点就是平衡因子的更新,对于这个问题,我们可以先总结一下上图,(90作为pParent, 30作为pCur, 60作为curR)左右单旋的结果其实使把curR的左子树与pCur链接,curR的右子树与pParent链接,然后curR作为新树的根,那么平衡因子的修改就需要根据60的平衡因子为状况进行修改了,curR的平衡因子一共有三种情况(-1/0/1).我们逐步分析:
- curR是新插入的节点 ——
curR的平衡因子是0,相当于上图中h等于0的情况
插入后
pParent,pCur和curR的平衡因子都变成0
- 插入在curR的左子树 ——
curR的平衡因子是-1
由于插入后
curR的左子树交给了pCur,也就是上图中的情况,此时pCur和curR的平衡因子都变成0,pParent的平衡因子变成1
- 插入在curR的右子树——
curR的平衡因子是1
对应的就是上图中c的高度是h, b的高度是h - 1, 此时pParent 和 curR的平衡因子都变成0, pCur的平衡因子变成-1
因此,旋转后平衡因子的改变是根据curR的平衡因子的状况就行分类修改的,并且由于上文中我们定义了左右旋转的函数,直接复用就可以得到左右单选的函数,代码如下:
void reverseRL(node* parent){node* cur = parent->_right, * curL = cur->_left;int bf = curL->_bf;reverseR(cur);reverseL(parent);if (bf == 0)cur->_bf = parent->_bf = curL->_bf = 0;else if (bf == -1){cur->_bf = 1;parent->_bf = curL->_bf = 0;}else if (bf == 1){parent->_bf = -1;cur->_bf = curL->_bf = 0;}elsethrow "balance factor out_of_range";}
新节点插入较高右子树的左侧:右左单旋
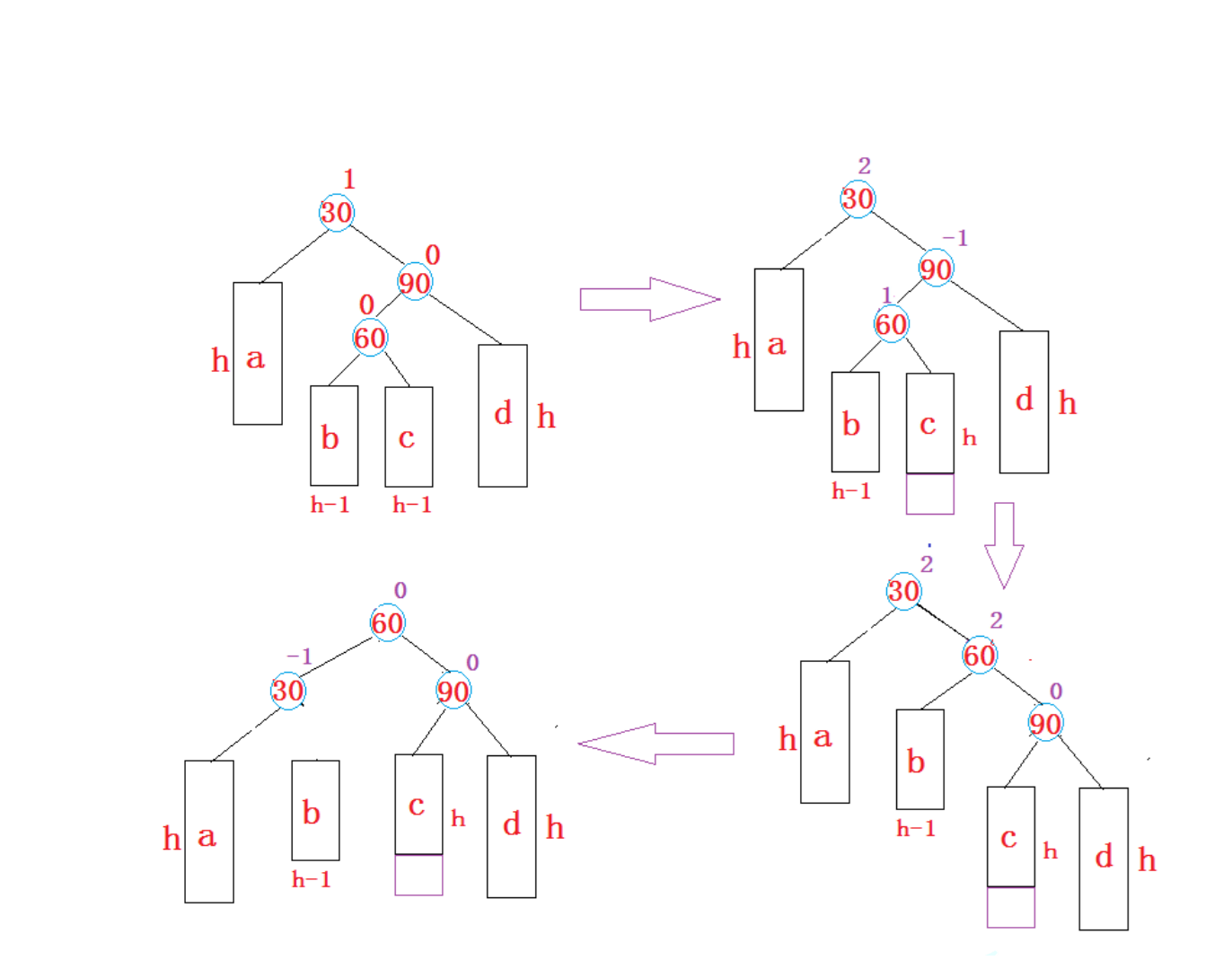
这里的思考方式和右左单选相同,留给大家自己思考。
旋转总结
假如以pParent为根的子树不平衡,即pParent的平衡因子为±2,分以下情况考虑:
- pParent的平衡因子为2,说明pParent的右子树高,设pParent的右子树的根为pCur
- 当pCur的平衡因子为1是,执行左单旋
- 如果是-1,执行右左单选
- pParent的平衡因子为-2,说明pParent的左子树高,设pParent的左子树的根为pCur
- 当pCur的平衡因子为-1时,执行右单旋
- 当pCur的平衡因子为1时,执行左右单旋
另外,我们可以发现旋转完成之后,当前根的平衡因子都变成了0,因此不需要继续向上更新
AVL树插入完整代码
public:bool insert(const pair<K, V>& kv){//如果头节点为空,直接将值赋给头节点即可if (!_root){node* newNode = new node(kv.first, kv.second);_root = newNode;return true;}//如果不为空,寻找插入位置node* parent = nullptr, *cur = _root;while (cur){auto& key = cur->_kv.first;parent = cur;if (kv.first > key)cur = cur->_right;else if (kv.first < key)cur = cur->_left;else return false;}node* newNode = new node(kv.first, kv.second);//循环结束,找到插入位置if (parent->_kv.first < kv.first)parent->_right = newNode;elseparent->_left = newNode;newNode->_parent = parent;cur = newNode;//更新平衡因子while (parent){//先修改因子//判断新增节点的方位对parent的平衡因子进行处理if (parent->_right == cur)parent->_bf++;elseparent->_bf--;if (parent->_bf == 0) break;//如果parent的平衡因子为±1,继续处理else if (abs(parent->_bf) == 1){cur = parent;parent = parent->_parent;}else if (abs(parent->_bf) == 2){//进行翻转操作if (parent->_bf == 2 && cur->_bf == 1) reverseL(parent);else if (parent->_bf == -2 && cur->_bf == -1)reverseR(parent);else if (parent->_bf == 2 && cur->_bf == -1) reverseRL(parent);else if (parent->_bf == -2 && cur->_bf == 1) reverseLR(parent);break;}//由于平衡因子的情况只有以上五种,出现其他种类的平衡因子说明AVL树已经被破坏//通过抛异常来显示else throw "the bf out_of_range";}return true;}
private:void reverseL(node* parent){node* ppnode = parent->_parent, *cur = parent->_right;node* curL = cur->_left;// 连接parent和curLeftparent->_right = curL;if (curL) curL->_parent = parent;// 连接parent和curcur->_left = parent;parent->_parent = cur;//跟新parent和cur的平衡因子parent->_bf = cur->_bf = 0;//更新根节点或者与ppnode的连接关系if (ppnode){if (ppnode->_right == parent)ppnode->_right = cur;elseppnode->_left = cur;cur->_parent = ppnode;}else{_root = cur;cur->_parent = nullptr;}}void reverseR(node* parent){node* cur = parent->_left, *ppnode = parent->_parent;node* curR = cur->_right;//连接parent和curRparent->_left = curR;if (curR)curR->_parent = parent;//连接cur和parentcur->_right = parent;parent->_parent = cur;//连接ppnode和curcur->_parent = ppnode;if (ppnode){if (ppnode->_right == parent)ppnode->_right = cur;elseppnode->_left = cur;}else_root = cur;//跟新bfparent->_bf = cur->_bf = 0;}void reverseRL(node* parent){node* cur = parent->_right, * curL = cur->_left;int bf = curL->_bf;reverseR(cur);reverseL(parent);if (bf == 0)cur->_bf = parent->_bf = curL->_bf = 0;else if (bf == -1){cur->_bf = 1;parent->_bf = curL->_bf = 0;}else if (bf == 1){parent->_bf = -1;cur->_bf = curL->_bf = 0;}elsethrow "balance factor out_of_range";}void reverseLR(node* parent){node* cur = parent->_left;node* curR = cur->_right;int bf = curR->_bf;reverseL(cur);reverseR(parent);if (bf == 0)cur->_bf = parent->_bf = curR->_bf = 0;else if (bf == -1){parent->_bf = -1;cur->_bf = curR->_bf = 0;}else if (bf == 1){cur->_bf = 1;curR->_bf = parent->_bf = 0;}else throw"balance factor out_of_range";}
AVL树的验证
可以通过监视窗口进行验证,但是这样过于麻烦,我们可以设计一个验证函数:
验证其为二叉搜索树
如果中序遍历能够得到一个有序序列,那就说明是二叉搜索树
public:void inorder() {_inorder(_root); cout << endl;return;}
private:void _inorder(node* root){if (!root) return;_inorder(root->_left);cout << root->_kv.first << ' ' << root->_kv.second << endl;_inorder(root->_right);}
验证其为平衡树
- 每个节点子树的高度绝对值不超过1
- 验证节点的平衡因子是否计算正确
博主采用的是回溯的方法来验证,先验证左子树和右子树是否为AVL_Tree,同时返回该树的高度,用于验证上层的树是否为AVL_Tree。
代码如下:
public:void is_AVL() {auto ret = _is_AVL(_root); if (ret.second) cout << "this tree is AVL_tree\n";}
private:pair<int, bool> _is_AVL(node* root){pair<int, bool> ret{ 0, true };if (!root) return ret;auto ret_left = _is_AVL(root->_left);auto ret_right = _is_AVL(root->_right);ret.second = ret_left.second && ret_right.second;//判断平衡因子是否正确int ans_bf = ret_right.first - ret_left.first;if (ans_bf != root->_bf){printf("平衡因子计算错误,正确平衡因子: %d, 当前平衡因子:%d", ans_bf, root->_bf);ret.second = false;}if (abs(ans_bf) >= 2){cout << "平衡因子超过最大值\n";ret.second = false;}ret.first = max(ret_left.first, ret_right.first) + 1;return ret;}
AVL树的删除
因为AVL树也是搜索二叉树,所以可以按照搜索二叉树的方式将节点删除,然后只需要加入更新平衡因子的步骤就可以了,比较不同的是删除操作下平衡因子的更新是如果删除后节点的平衡因子为0还需要继续更新,而如果是±1不需要继续更新,±2进行旋转,但是旋转完成之后由于根的平衡因子变成了0,还有可能需要继续向上更新。
AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这 样可以保证查询时高效的时间复杂度,即 l o g 2 ( N ) log_2 (N) log2(N)。但是如果要对AVL树做一些结构修改的操 作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时, 有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数 据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
完整实现代码
template<typename K, typename V>
struct TreeNode
{pair<K, V> _kv;TreeNode<K, V>* _parent = nullptr;TreeNode<K, V>* _left = nullptr;TreeNode<K, V>* _right = nullptr;int _bf = 0;TreeNode(const K& key, const V& value):_kv({ key, value }){}
};template<typename K, typename V>
class AVL_Tree
{typedef TreeNode<K, V> node;
private:node* _root = nullptr;
public:bool insert(const pair<K, V>& kv){//如果头节点为空,直接将值赋给头节点即可if (!_root){node* newNode = new node(kv.first, kv.second);_root = newNode;return true;}//如果不为空,寻找插入位置node* parent = nullptr, *cur = _root;while (cur){auto& key = cur->_kv.first;parent = cur;if (kv.first > key)cur = cur->_right;else if (kv.first < key)cur = cur->_left;else return false;}node* newNode = new node(kv.first, kv.second);//循环结束,找到插入位置if (parent->_kv.first < kv.first)parent->_right = newNode;elseparent->_left = newNode;newNode->_parent = parent;cur = newNode;//更新平衡因子while (parent){//先修改因子//判断新增节点的方位对parent的平衡因子进行处理if (parent->_right == cur)parent->_bf++;elseparent->_bf--;if (parent->_bf == 0) break;//如果parent的平衡因子为±1,继续处理else if (abs(parent->_bf) == 1){cur = parent;parent = parent->_parent;}else if (abs(parent->_bf) == 2){//进行翻转操作if (parent->_bf == 2 && cur->_bf == 1) reverseL(parent);else if (parent->_bf == -2 && cur->_bf == -1)reverseR(parent);else if (parent->_bf == 2 && cur->_bf == -1) reverseRL(parent);else if (parent->_bf == -2 && cur->_bf == 1) reverseLR(parent);break;}//由于平衡因子的情况只有以上五种,出现其他种类的平衡因子说明AVL树已经被破坏//通过抛异常来显示else throw "the bf out_of_range";}return true;}void inorder() {_inorder(_root); cout << endl;return;}void is_AVL() {auto ret = _is_AVL(_root); if (ret.second) cout << "this tree is AVL_tree\n";}
private:void reverseL(node* parent){node* ppnode = parent->_parent, *cur = parent->_right;node* curL = cur->_left;// 连接parent和curLeftparent->_right = curL;if (curL) curL->_parent = parent;// 连接parent和curcur->_left = parent;parent->_parent = cur;//跟新parent和cur的平衡因子parent->_bf = cur->_bf = 0;//更新根节点或者与ppnode的连接关系if (ppnode){if (ppnode->_right == parent)ppnode->_right = cur;elseppnode->_left = cur;cur->_parent = ppnode;}else{_root = cur;cur->_parent = nullptr;}}void reverseR(node* parent){node* cur = parent->_left, *ppnode = parent->_parent;node* curR = cur->_right;//连接parent和curRparent->_left = curR;if (curR)curR->_parent = parent;//连接cur和parentcur->_right = parent;parent->_parent = cur;//连接ppnode和curcur->_parent = ppnode;if (ppnode){if (ppnode->_right == parent)ppnode->_right = cur;elseppnode->_left = cur;}else_root = cur;//跟新bfparent->_bf = cur->_bf = 0;}void reverseRL(node* parent){node* cur = parent->_right, * curL = cur->_left;int bf = curL->_bf;reverseR(cur);reverseL(parent);if (bf == 0)cur->_bf = parent->_bf = curL->_bf = 0;else if (bf == -1){cur->_bf = 1;parent->_bf = curL->_bf = 0;}else if (bf == 1){parent->_bf = -1;cur->_bf = curL->_bf = 0;}elsethrow "balance factor out_of_range";}void reverseLR(node* parent){node* cur = parent->_left;node* curR = cur->_right;int bf = curR->_bf;reverseL(cur);reverseR(parent);if (bf == 0)cur->_bf = parent->_bf = curR->_bf = 0;else if (bf == -1){parent->_bf = -1;cur->_bf = curR->_bf = 0;}else if (bf == 1){cur->_bf = 1;curR->_bf = parent->_bf = 0;}else throw"balance factor out_of_range";}//需要知道两个东西,层数高度以及高度差pair<int, bool> _is_AVL(node* root){pair<int, bool> ret{ 0, true };if (!root) return ret;auto ret_left = _is_AVL(root->_left);auto ret_right = _is_AVL(root->_right);ret.second = ret_left.second && ret_right.second;//判断平衡因子是否正确int ans_bf = ret_right.first - ret_left.first;if (ans_bf != root->_bf){printf("平衡因子计算错误,正确平衡因子: %d, 当前平衡因子:%d", ans_bf, root->_bf);ret.second = false;}if (abs(ans_bf) >= 2){cout << "平衡因子超过最大值\n";ret.second = false;}ret.first = max(ret_left.first, ret_right.first) + 1;return ret;}void _inorder(node* root){if (!root) return;_inorder(root->_left);cout << root->_kv.first << ' ' << root->_kv.second << endl;_inorder(root->_right);}};
总结
AVL树的出现较为有效的解决了二叉搜索树在极端情况下效率低下的问题,但还处理的不够完善,因此,后面又出现了红黑树,对于AVL树在一些地方会更有优势,红黑树博主在之后也会讲解!关于AVL树的知识就到此结束了,如果大家有什么疑惑或者发现博主写的有哪些问题,欢迎在评论区指出!
相关文章:

数据结构——AVL树(详解 + C++模拟实现)
文章目录 前言AVL树的概念AVL树节点的定义AVL树类框架AVL树的插入AVL树的旋转新节点插入较高子树的左侧 —— 左左: 右单旋新节点插入较高右子树的右侧——右右: 左单旋新节点插入较高左子树的右侧 —— 左右: 先左单旋然后再有单旋新节点插入较高右子树的左侧&…...

redis 雪崩,穿透,击穿及解决方案
一、缓存雪崩: 1. 原因: 缓存雪崩是指在我们设置缓存时大量采用了相同的过期时间,导致缓存在某一时刻同时失效,请求全部转发到DB,DB瞬时压力过重雪崩。 2. 解决方案: 将失效时间分散,通过生成随机数使得key的过期时间…...
Flutter环境搭建及新建项目
一、下载安装压缩包 https://storage.flutter-io.cn/flutter_infra_release/releases/stable/windows/flutter_windows_3.10.6-stable.zip 二、解压缩 解压之后,将里面的flutter整体拿出来 三、配置环境变量 将flutter/bin全路径配置到系统环境变量里面 四、运行…...

【面试题精讲】深拷贝和浅拷贝区别了解吗?什么是引用拷贝?
“ 有的时候博客内容会有变动,首发博客是最新的,其他博客地址可能会未同步,认准https://blog.zysicyj.top ” 首发博客地址[1] 面试题手册[2] 系列文章地址[3] 深拷贝和浅拷贝的区别: 深拷贝(Deep Copy)和浅拷贝&#…...

CentOS7.9中使用packstack安装train版本
这里写目录标题 材料准备为什么选择packstack安装静态ip系统配置使用阿里云yum源安装packstack部署openstack 材料准备 ecs云服务器8核心16g内存一台,系统盘100GB,系统CentOS7.9vpc网段:192.168.0.1/24eip一个,带宽5M以上 为什么…...

mfw git泄露构造闭合
这题也挺有想法 第一次确实没有想到 首先我们可以扫出 git 然后 我们githack 泄露一下 然后我们看index.php代码 <?phpif (isset($_GET[page])) {$page $_GET[page]; } else {$page "home"; }$file "templates/" . $page . ".php";/…...
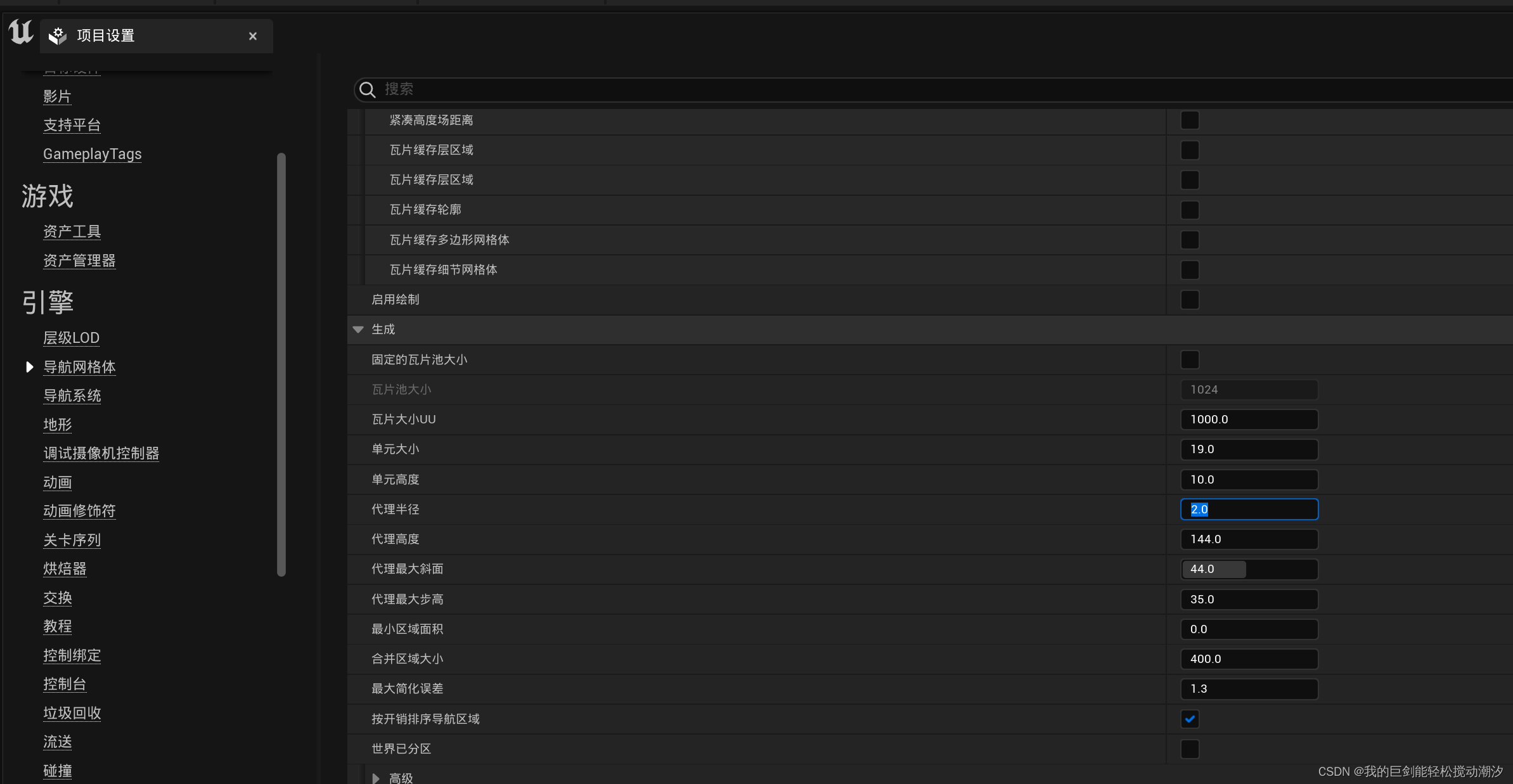
UE5修改导航网格的参数
Unreal Engine 4 - Recast NavMesh Size, how to Change Agent Radius / Tutorial - YouTubehttps://www.youtube.com/watch?vf3hF6xdmCTk 修改当前的 代理半径就是一般贴边的长度 修改编辑器的...
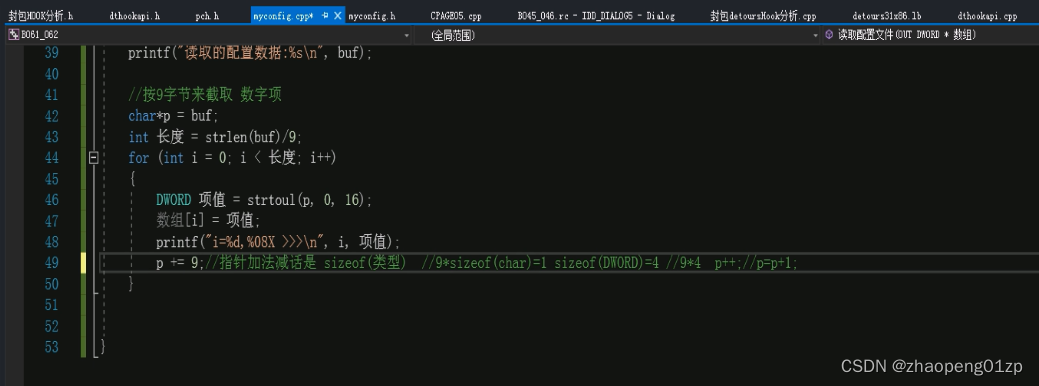
郁金香2021年游戏辅助技术中级班(七)
郁金香2021年游戏辅助技术中级班(七) 058-C,C写代码HOOK分析封包数据格式A059-C,C写代码HOOK分析封包数据格式B-detours劫持060-C,C写代码HOOK分析封包数据格式C-过滤和格式化061-C,C写代码HOOK分析封包数据格式D-写入配置文件062-C,C写代码HOOK分析封包…...
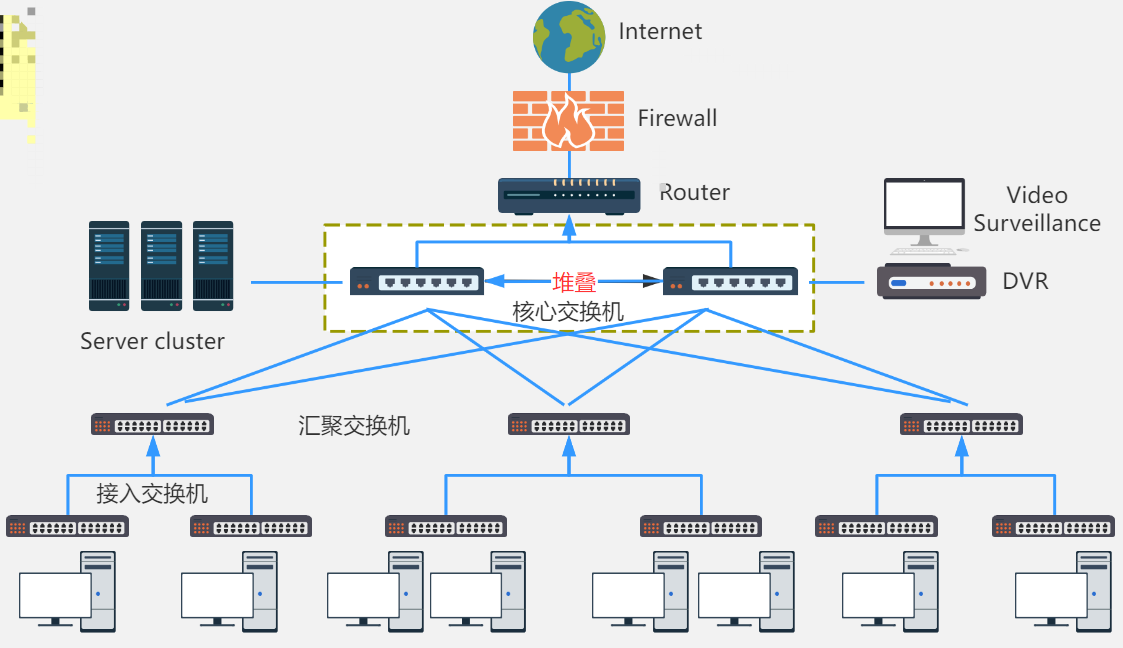
【网络】路由器和交换机的区别
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_Linux,大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的帮助…...
 函数、COALESCE()函数、DATEDIFF()函数)
SQL的CASE WHEN函数、CAST函数、CONVERT() 函数、COALESCE()函数、DATEDIFF()函数
一、CASE WHEN简单使用 SELECT CASE WHEN age > 18 AND age < 25 THEN 18-25WHEN age > 25 AND age < 35 THEN 25-35WHEN age > 35 AND age < 45 THEN 36-45ELSE 45END AS age_groupFROM peopleGROUP BY age_group;二、CASE WHEN语句与聚合函数一起使用 SE…...
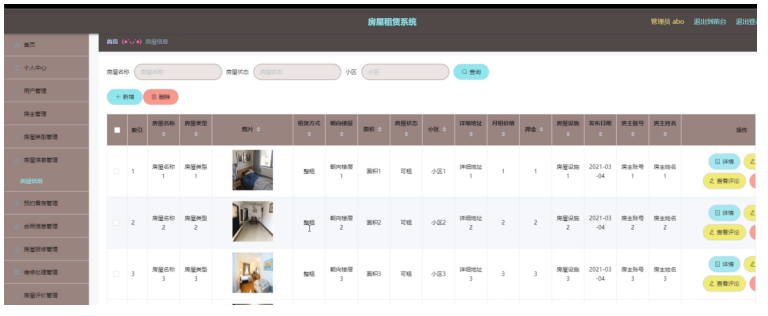
前后端分离计算机毕设项目之基于springboot+vue的房屋租赁系统《内含源码+文档+部署教程》
博主介绍:✌全网粉丝10W,前互联网大厂软件研发、集结硕博英豪成立工作室。专注于计算机相关专业毕业设计项目实战6年之久,选择我们就是选择放心、选择安心毕业✌ 🍅由于篇幅限制,想要获取完整文章或者源码,或者代做&am…...

《Spring框架前世今生》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

基于树种优化的BP神经网络(分类应用) - 附代码
基于树种优化的BP神经网络(分类应用) - 附代码 文章目录 基于树种优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.树种优化BP神经网络3.1 BP神经网络参数设置3.2 树种算法应用 4.测试结果:5.M…...

纳百川冲刺创业板上市:计划募资约8亿元,宁德时代为主要合作方
近日,纳百川新能源股份有限公司(下称“纳百川”)向深交所创业板递交的上市申请材料获得受理,浙商证券为其独家保荐人。 本次冲刺上市,纳百川计划募资8.29亿元,将用于纳百川(滁州)新能…...

light client轻节点简介
1. 引言 前序博客: Helios——a16z crypto构建的去中心化以太坊轻节点 去中心化和自我主权对于Web3的未来至关重要,但是这些理想并不总适用于每个项目或应用程序。在非托管钱包和bridges等工具中严格优先考虑安全性而不是便利性的用户,可选…...

1500*B. Zero Array(贪心数学找规律)
Problem - 1201B - Codeforces 解析: 因为每次减少2,如果总和为奇数肯定无法实现。 特例,如果某个数大于其他所有数的总和,同样无法实现。 其他均可实现。 #include<bits/stdc.h> using namespace std; #define int long l…...
java Spring Boot整合jwt实现token生成并验证效果
先在 pom.xml 文件中注入依赖 <!-- JWT --> <dependency><groupId>io.jsonwebtoken</groupId><artifactId>jjwt-api</artifactId><version>0.11.2</version> </dependency> <dependency><groupId>io.jsonw…...

基础-MVP图像处理-仿射变换
仿射变换算子可以将输入图像矩形区域的图像进行变换,并生成新的矩形输出图像。 可对图像进行截取、缩放、倾斜、旋转等操作,矫正图像到无倾斜,配合其他算子使用。 配置界面:可以调整其位置、大小、旋转和倾斜程度,缩放…...

Linux嵌入式学习之Ubuntu入门(六)shell脚本详解
系列文章内容 Linux嵌入式学习之Ubuntu入门(一)基本命令、软件安装、文件结构、编辑器介绍 Linux嵌入式学习之Ubuntu入门(二)磁盘文件介绍及分区、格式化等 Linux嵌入式学习之Ubuntu入门(三)用户、用户组…...

学习完C++ 并发编程后 手写线程池 最简单的线程池
目录 精简版注释: //线程安全的队列容器(精简版) 最简易可行的线程池(精简版) 详细版注释: //线程安全的队列容器(详细版) 最简易可行的线程池(详细版࿰…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...