机器学习算法基础--KNN算法分类
文章目录
- 1.KNN算法原理介绍
- 2.KNN分类决策原则
- 3.KNN度量距离介绍
- 3.1.闵可夫斯基距离
- 3.2.曼哈顿距离
- 3.3.欧式距离
- 4.KNN分类算法实现
- 5.KNN分类算法效果
- 6.参考文章与致谢
1.KNN算法原理介绍
KNN(K-Nearest Neighbor)工作原理:
在一个存在标签的数据集中,当我们输入一个新的没有标签的样本时候,KNN算法的任务就是将该样本分类,即给定其对应的样本标签。
输入没有标签的数据后,将新数据中的每个特征与样本集中数据对应的特征进行比较,提取出样本集中特征最相似数据(最近邻)的分类标签。
一般来说我们选取的是新样本的最近的k个样本进行"投票"决策,这就是KNN算法中k的意思,
通常k是不大于20的整数。最后选择k个最相似数据中出现次数最多的分类作为新数据的分类。
2.KNN分类决策原则
KNN算法一般是用多数表决方法,即由输入实例的K个邻近的多数类决定输入实例的类。这种思想也是经验风险最小化的结果。
训练样本为 ( x i , y i ) (x_{i} ,y_{i}) (xi,yi)。当输入实例为 x,标记为c, N k ( x ) N_{_k}(x) Nk(x)是输入实例x的k近邻训练样本集。我们定义训练误差率是K近邻训练样本标记与输入标记不一致的比例,误差率表示为:
1 k ∑ x i ∈ N k ( x ) I ( y i ≠ c j ) = 1 − 1 k ∑ x i ∈ N k ( x ) I ( y i = c j ) \frac1k\sum_{x_i\in N_{k}(x)}I(y_i\neq c_j)=1-\frac1k\sum_{x_i\in N_{k}(x)}I(y_i=c_j)\quad k1xi∈Nk(x)∑I(yi=cj)=1−k1xi∈Nk(x)∑I(yi=cj)
因此,要使误差率最小化即经验风险最小,就要使 1 k ∑ x i ∈ N k ( x ) I ( y i = c j ) \frac{1}{k}\sum_{x_{i}\in N_{k}(x)}I(y_{i}=c_{j}) k1∑xi∈Nk(x)I(yi=cj)尽可能大,即K近邻的标记值尽可能的与输入标记一致,所以多数表决规则等价于经验风险最小化。
3.KNN度量距离介绍
3.1.闵可夫斯基距离
闵可夫斯基距离表示如下所示:
D ( x , y ) = ∣ x 1 − y 1 ∣ p + ∣ x 2 − y 2 ∣ p + . . . + ∣ x n − y n ∣ p p = ∑ i = 1 n ∣ x i − y i ∣ p p \begin{aligned} D(x,y)& =\sqrt[p]{\mid x_1-y_1\mid^p+\mid x_2-y_2\mid^p+...+\mid x_n-y_n\mid^p} \\ &=\sqrt[p]{\sum_{i=1}^{n}\mid x_{i}-y_{i}\mid^{p}} \end{aligned} D(x,y)=p∣x1−y1∣p+∣x2−y2∣p+...+∣xn−yn∣p=pi=1∑n∣xi−yi∣p
3.2.曼哈顿距离
曼哈顿距离如下所示:
D ( x , y ) = ∣ x 1 − y 1 ∣ + ∣ x 2 − y 2 ∣ + . . . . + ∣ x n − y n ∣ = ∑ i = 1 n ∣ x i − y i ∣ \begin{aligned} D(x,y)& =\mid x_1-y_1\mid+\mid x_2-y_2\mid+....+\mid x_n-y_n\mid \\ &=\sum_{i=1}^{n}\mid x_{i}-y_{i}\mid \end{aligned} D(x,y)=∣x1−y1∣+∣x2−y2∣+....+∣xn−yn∣=i=1∑n∣xi−yi∣
3.3.欧式距离
欧式距离如下所示:
D ( x , y ) = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + . . . + ( x n − y n ) 2 = ∑ i = 1 n ( x i − y i ) 2 \begin{aligned} D(x,y)& =\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+...+(x_n-y_n)^2} \\ &=\sqrt{\sum_{i=1}^{n}(x_{i}-y_{i})^{2}} \end{aligned} D(x,y)=(x1−y1)2+(x2−y2)2+...+(xn−yn)2=i=1∑n(xi−yi)2
4.KNN分类算法实现
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine# 支持中文
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号#加载wine数据集
data = load_wine()
X = data.data[:, :2] #取前两列内容作为Alcohol和苹果酸作为样本
y = data.target#划分数据集和测试集
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=42)#创建KNN分类器,设置k=6
knn_classifier = KNeighborsClassifier(n_neighbors=10, metric='euclidean')#以欧式距离作为度量距离
knn_classifier.fit(X_train, y_train)# 预测测试集
y_pred = knn_classifier.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
Accuracy: 0.8888888888888888
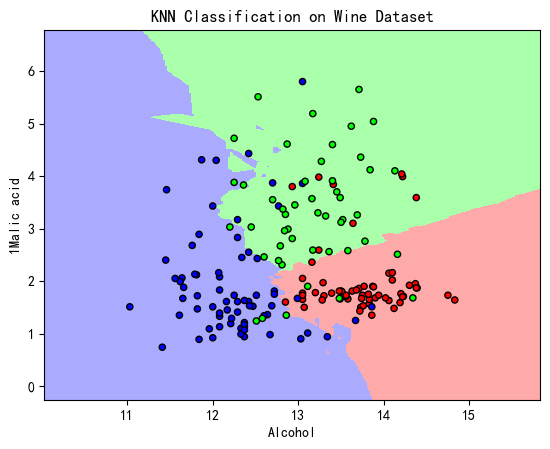
5.KNN分类算法效果
#可视化绘图
h = .02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))# 获取预测结果
Z = knn_classifier.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)# 创建颜色地图
cmap_background = ListedColormap(['#FFAAAA', '#AAAAFF', '#AAFFAA'])
cmap_points = ListedColormap(['#FF0000', '#0000FF', '#00FF00'])# 可视化结果
plt.pcolormesh(xx, yy, Z, cmap=cmap_background)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_points,edgecolor='k', s=20)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("KNN Classification on Wine Dataset")
plt.xlabel("Alcohol")
plt.ylabel("1Malic acid")
plt.show()
6.参考文章与致谢
本章内容的完成离不开大佬文章的启发和帮助,在这里列出名单,如果对于内容还有不懂的,可以移步对应的文章进行进一步的理解分析。
1.KNN算法:https://blog.csdn.net/qq_42722197/article/details/123196332?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522169665324816800182743993%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=169665324816800182743993&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_click~default-2-123196332-null-null.142^v95^chatgptT3_1&utm_term=knn%E7%AE%97%E6%B3%95%E5%8E%9F%E7%90%86&spm=1018.2226.3001.4187
如果大家这这篇blog中有什么不明白的可以去他的专栏里面看看,内容非常全面,应该能够有比较好的解答。
在文章的最后再次表达由衷的感谢!!
相关文章:

机器学习算法基础--KNN算法分类
文章目录 1.KNN算法原理介绍2.KNN分类决策原则3.KNN度量距离介绍3.1.闵可夫斯基距离3.2.曼哈顿距离3.3.欧式距离 4.KNN分类算法实现5.KNN分类算法效果6.参考文章与致谢 1.KNN算法原理介绍 KNN(K-Nearest Neighbor)工作原理: 在一个存在标签的…...
深入探究 C++ 编程中的资源泄漏问题
目录 1、GDI对象泄漏 1.1、何为GDI资源泄漏? 1.2、使用GDIView工具排查GDI对象泄漏 1.3、有时可能需要结合其他方法去排查 1.4、如何保证没有GDI对象泄漏? 2、进程句柄泄漏 2.1、何为进程句柄泄漏? 2.2、创建线程时的线程句柄泄漏 …...

BLE协议栈1-物理层PHY
从应届生开始做ble开发也差不读四个月的时间了,一直在在做上层的应用,对蓝牙协议栈没有过多的时间去了解,对整体的大方向概念一直是模糊的状态,在开发时也因此遇到了许多问题,趁有空去收集了一下资料来完成了本次专栏&…...
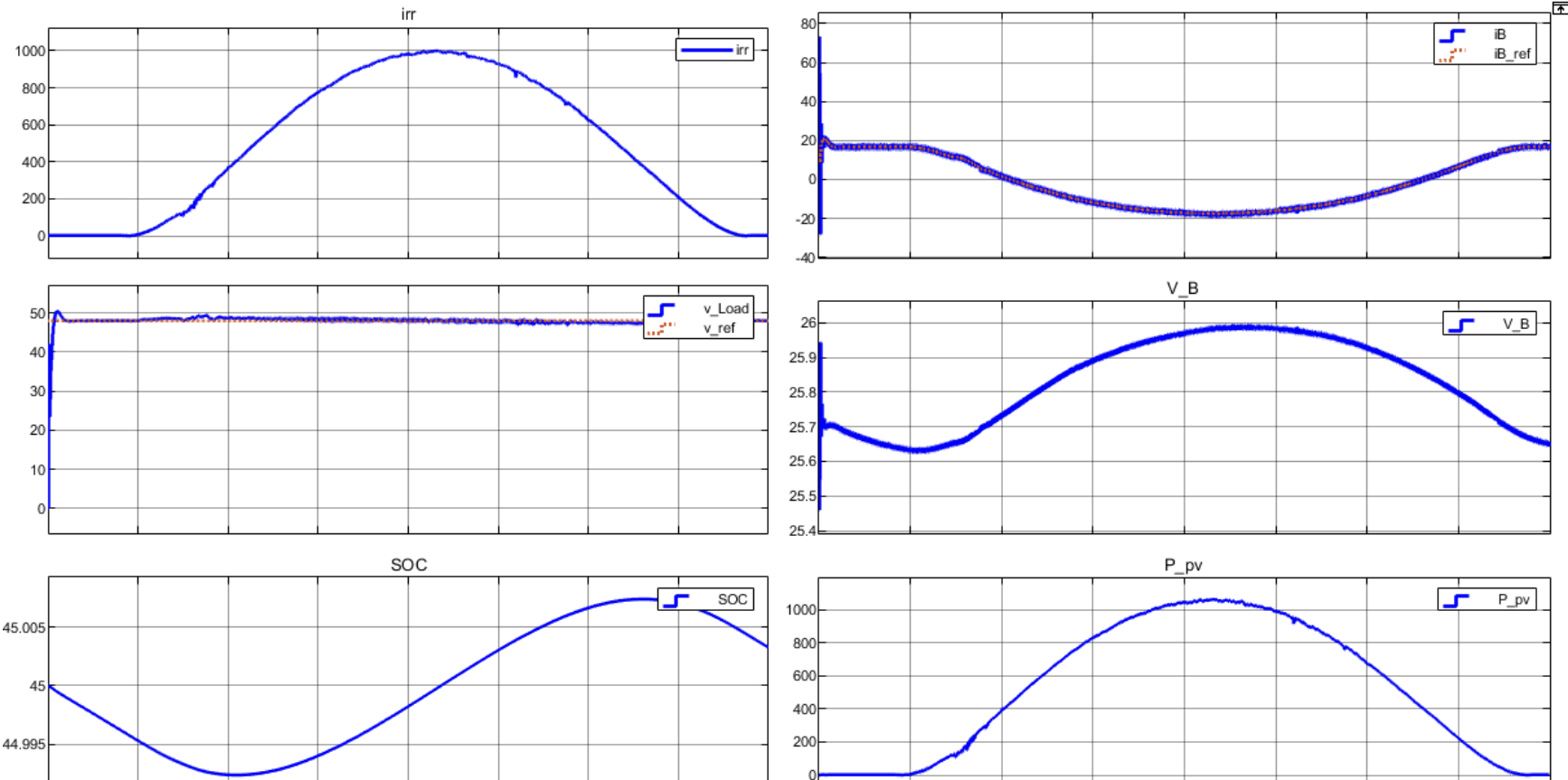
光伏储能直流系统MATLAB仿真(PV光伏阵列+Boost DCDC变换器+负载+双向DCDC变换器+锂离子电池系统)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

C++三大特性——继承(上篇)
文章目录 目录 一、继承的概念及定义 1.1继承的概念 1.2 继承定义 1.2.1定义格式 1.2.2继承关系和访问限定符 1.2.3继承基类成员访问方式的变化 二、基类和派生类对象赋值转换 三、继承中的作用域 四、派生类的默认成员函数 一、继承的概念及定义 1.1继承的概念 继承(inherita…...

docker系列(9) - docker-compose
文章目录 9. compose编排9.1 介绍9.2 安装9.3 compose常用命令9.4 实战Springboot部署9.4.1 准备组件配置文件9.4.1.1 redis的配置文件9.4.1.2 MySQL的配置文件9.4.1.3 SpringBoot打包文件 9.4.2 准备docker-compose.yml9.4.3 启动服务9.4.4 测试验证 9.5 实战ElasticsearchKib…...

Vue中如何进行日历展示与操作
在Vue中创建交互式日历应用 在Web开发中,创建一个交互式的日历应用是一项常见的任务。Vue.js作为一个流行的JavaScript框架,提供了许多便捷的工具和组件来简化日历的开发。本文将介绍如何使用Vue来创建一个简单但功能强大的日历应用,包括展示…...

SpringBoot 返回图片、Excel、音视频等流数据几种处理方式
方式一:直接针对响应对象(response)实现 @RestController @Slf4j @Api(tags = SwaggerConfig.TAG_IMAGE) @RequestMapping(SwaggerConfig.TAG_IMAGE) public class ImageController {@GetMapping(value = "/getImage")@ApiOperation("获取图片-以ImageIO流形…...
【Vue面试题一】、说说你对 Vue 的理解
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:有使用过vue吗ÿ…...

vue3 axios
npm install axios import axios from axios // 创建axios实例 const request axios.create({baseURL: ,// 所有的请求地址前缀部分(没有后端请求不用写)timeout: 80000, // 请求超时时间(毫秒)withCredentials: true,// 异步请求携带cookie// headers: {// 设置后端需要的传…...

划片机:半导体生产的必备设备
划片机是半导体加工行业中的重要设备,主要用于将晶圆切割成晶片颗粒,为后道工序粘片做好准备。随着国内半导体生产能力的提高,划片机市场的需求也在逐渐增加。 在市场定位上,划片机可以应用于半导体芯片和其他微电子器件的制造过程…...

电路维修——双端队列BFS
达达是来自异世界的魔女,她在漫无目的地四处漂流的时候,遇到了善良的少女翰翰,从而被收留在地球上。 翰翰的家里有一辆飞行车。有一天飞行车的电路板突然出现了故障,导致无法启动。电路板的整体结构是一个 R 行 C 列的网格&#…...
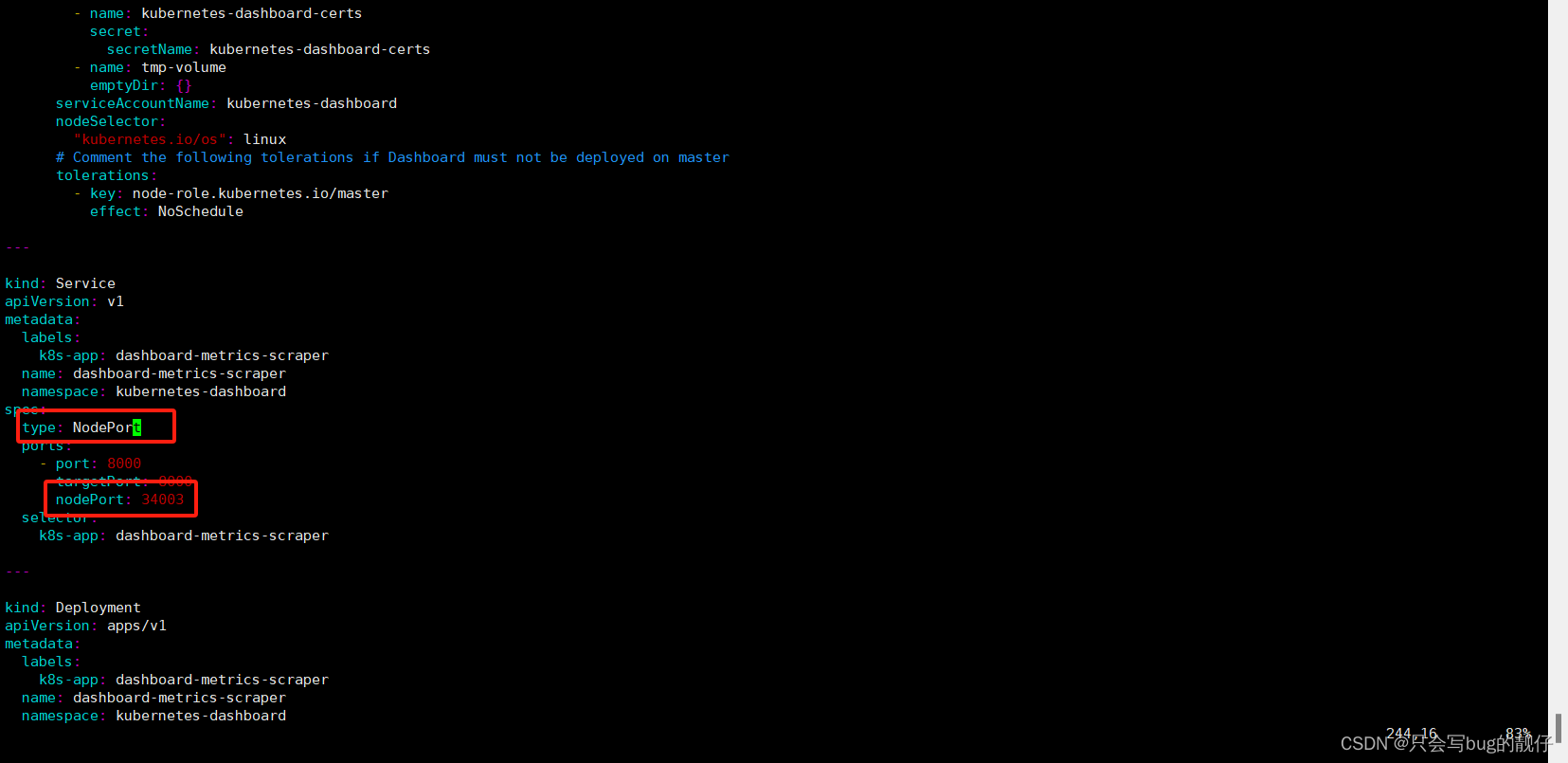
乌班图22.04 kubeadm简单搭建k8s集群
1. 我遇到的问题 任何部署类问题实际上对于萌新来说都不算简单,因为没有经验,这里我简单将部署的步骤和想法给大家讲述一下 2. 简单安装步骤 准备 3台标准安装的乌班图server22.04(采用vm虚拟机安装,ip为192.168.50.3࿰…...
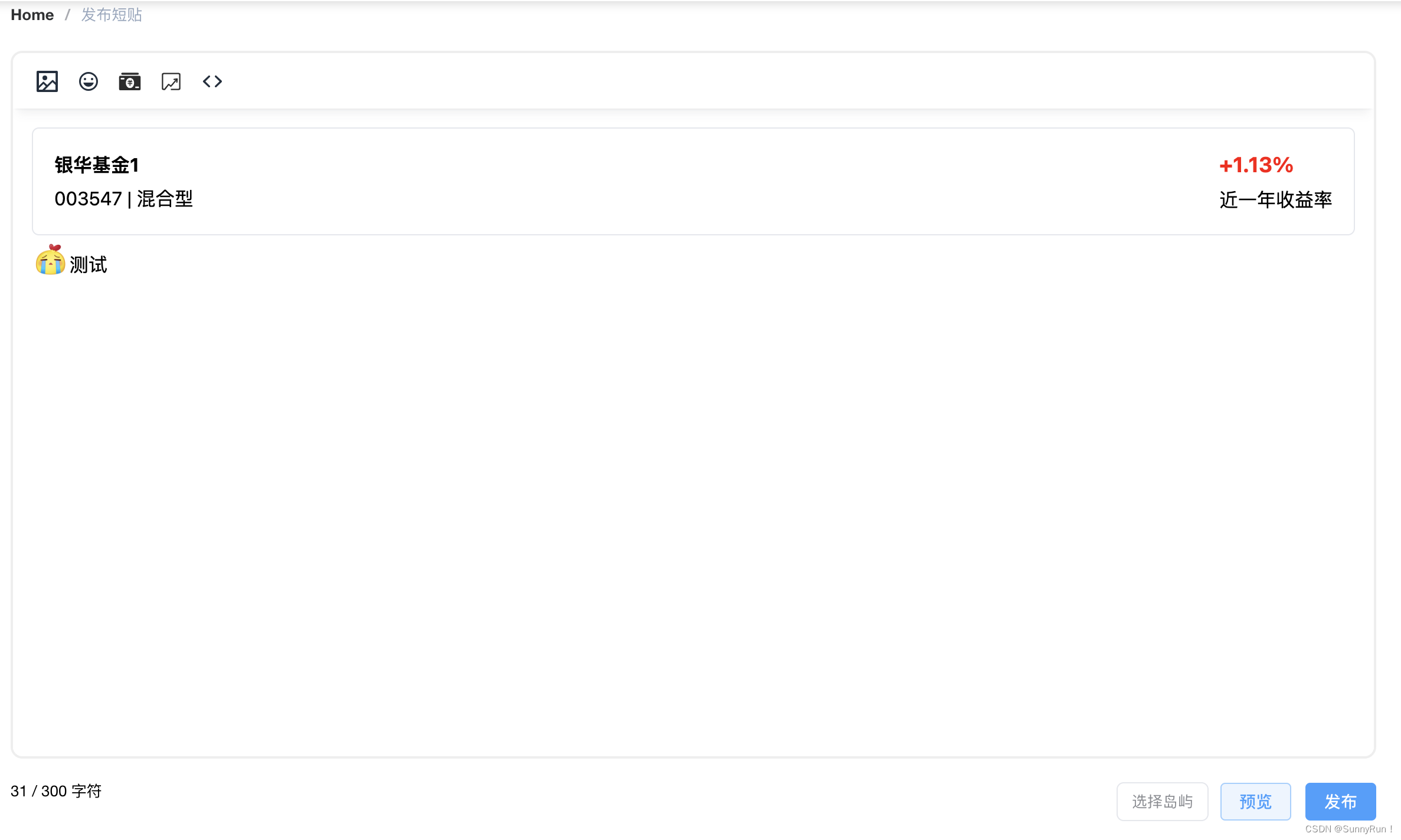
vue3富文本编辑器的二次封装开发-Tinymce
欢迎点击领取 -《前端面试题进阶指南》:前端登顶之巅-最全面的前端知识点梳理总结 *分享一个使用比较久的🪜 简介 1、安装:pnpm add tinymce / pnpm add tinymce/tinymce-vue > Vue3 tinymce tinymce/tinymce-vue 2、功能实现图片上传…...
typescript 类型声明文件
typescript 类型声明文件概述 在今天几乎所有的JavaScript应用都会引入许多第三方库来完成任务需求。这些第三方库不管是否是用TS编写的,最终都要编译成JS代码,才能发布给开发者使用。6我们知道是TS提供了类型,才有了代码提示和类型保护等机…...
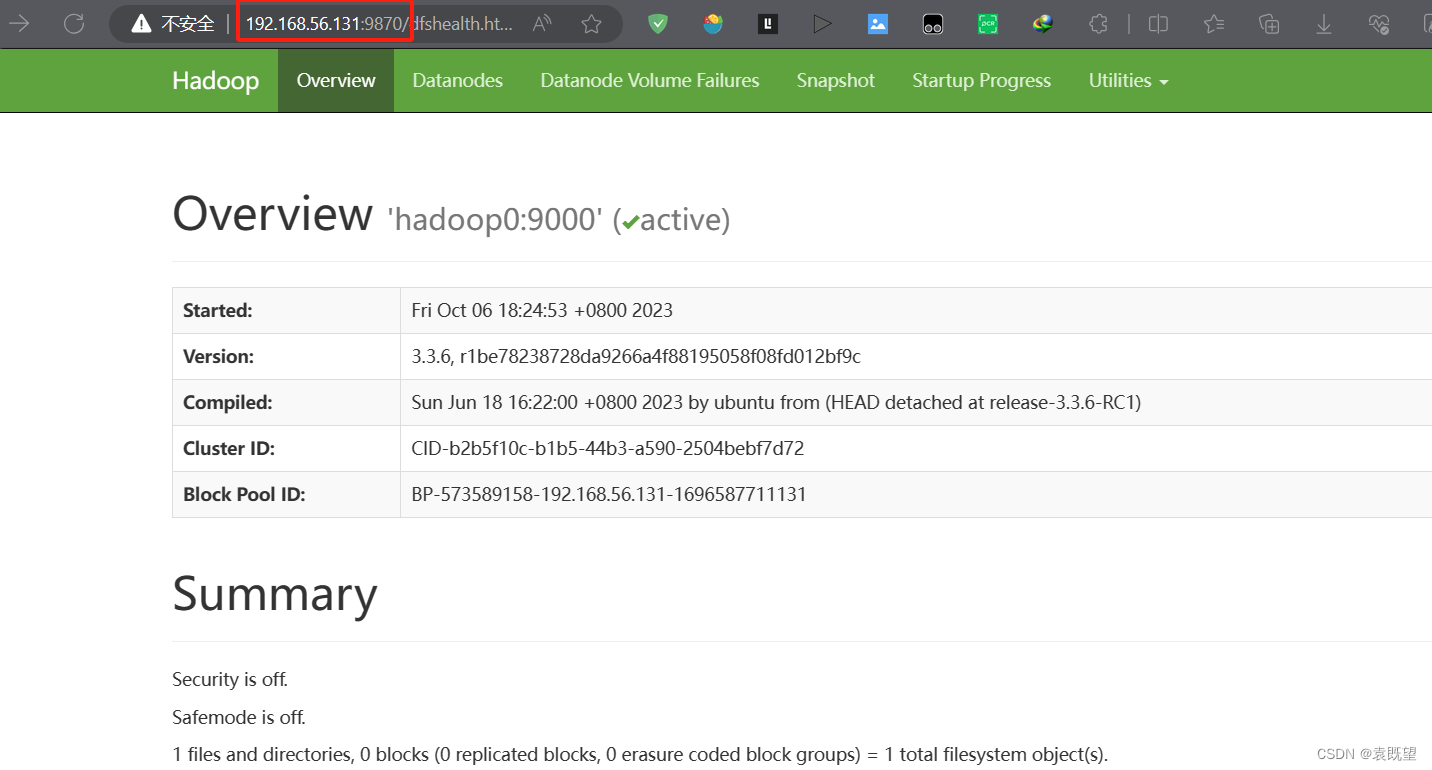
Hadoop伪分布式环境搭建
什么是Hadoop伪分布式集群? Hadoop 伪分布式集群是一种在单个节点上模拟分布式环境的配置,用于学习、开发和测试 Hadoop 的功能和特性。它提供了一个简化的方式来体验和熟悉 Hadoop 的各个组件,而无需配置和管理一个真正的多节点集群。 在 Ha…...
javaee ssm框架项目添加分页控件
搭建ssm框架项目 参考上一篇博文 添加分页控件 引入依赖 <?xml version"1.0" encoding"UTF-8"?><project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schema…...
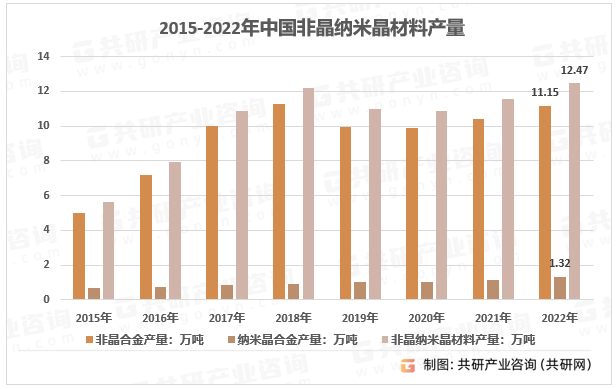
2023年中国非晶纳米晶竞争格局、产业链及行业产量分析[图]
非晶合金又称“液态金属、金属玻璃”,是一种新型软磁合金材料,主要包含铁、硅、硼等元素。其主要制品非晶合金薄带的制造工艺是采用急速冷却技术将合金熔液以每秒106℃的速度急速冷却,形成厚度约0.03mm的非晶合金薄带,物理状态表现…...
,递归处理。)
在业务开发中遇到的树形结构(部门、区域、职位),递归处理。
文章目录 概要对象结构示例完整示例小结 概要 本文主要记录在树形结构中会遇到的问题, 使用部门结构讲解,main方法进行演示。 1、获取部门树结构 2、根据部门id获取所有下级 3、根据部门id获取上级部门 4、根据部门id获取类似面包屑(总公司…...

张量-算术操作函数
tf.add(x,y,name None)求和函数 示例代码如下: import tensorflow.compat.v1 as tf tf.disable_v2_behavior()x 1 y 2a tf.add(x,y)with tf.Session() as sess:print(sess.run(a)) tf.subtract(x,y,name None)减法函数 示例代码如下: import tensorflow.compat.v1 as …...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
