【数据结构-哈希表 一】【原地哈希】:缺失的第一个正整数
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【原地哈希】,使用【数组】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为:目标公司+最近一年+出现频率排序,由高到低的去牛客TOP101去找,只有两个地方都出现过才做这道题(CodeTop本身汇聚了LeetCode的来源),确保刷的题都是高频要面试考的题。

明确目标题后,附上题目链接,后期可以依据解题思路反复快速练习,题目按照题干的基本数据结构分类,且每个分类的第一篇必定是对基础数据结构的介绍。
缺失的第一个正整数【MID】
又是一道考验数组结构与哈希表结合的题
题干
直接粘题干和用例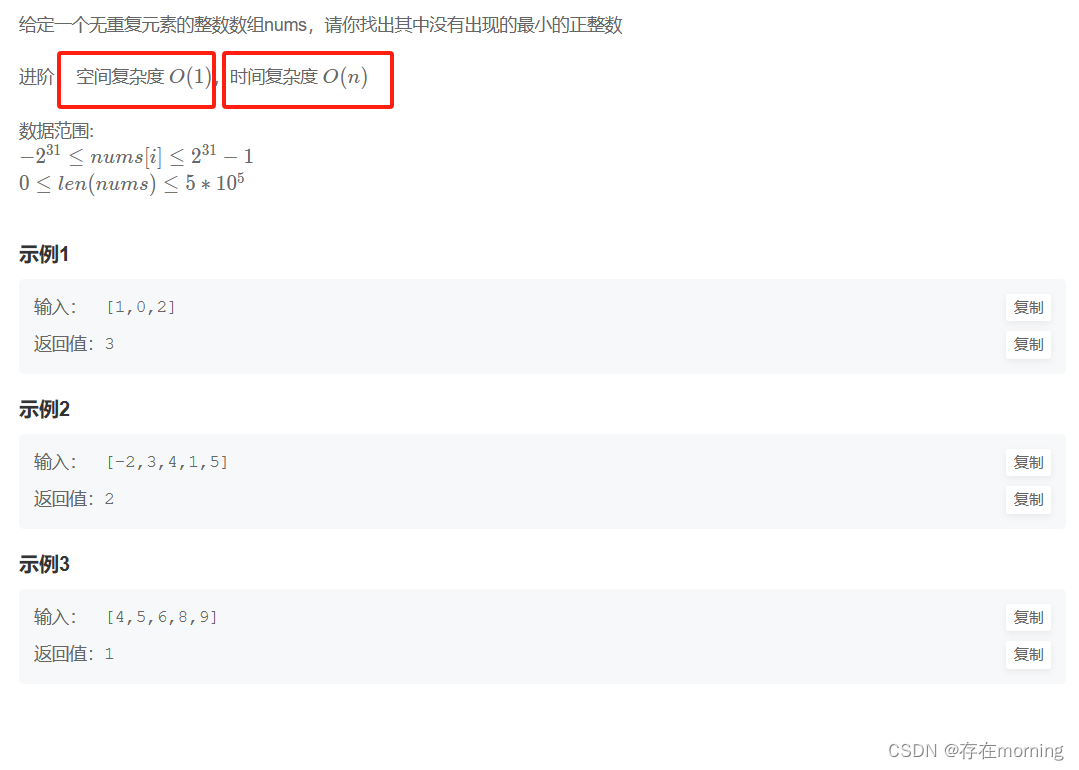
解题思路
原题解地址由于题目要求我们「只能使用常数级别的空间」,而要找的数一定在 [1, N + 1] 左闭右闭(这里 N 是数组的长度)这个区间里。因此,我们可以就把原始的数组当做哈希表来使用。事实上,哈希表其实本身也是一个数组,我们要找的数就在 [1, N + 1] 里,最后 N + 1 这个元素我们不用找。因为在前面的 N 个元素都找不到的情况下,我们才返回 N + 1;
- ** 按照桶排序思路进行预处理:保证 1 出现在 nums[0] 的位置上,2 出现在 nums[1] 的位置上,…,n 出现在 nums[n - 1] 的位置上。不在 [1, n] 范围内的数不用动**。例如样例中 [3,4,-1,1] 将会被预处理成 [1,-1,3,4]。
- 遍历 nums,找到第一个不在应在位置上的 [1, n] 的数。如果没有找到,说明数据连续,答案为 n + 1。例如样例预处理后的数组 [1,-1,3,4] 中第一个 nums[i] != i + 1 的是数字 2(i = 1)。
这个思想就相当于我们自己编写哈希函数,这个哈希函数的规则特别简单,那就是数值为 i 的数映射到下标为 i - 1 的位置。
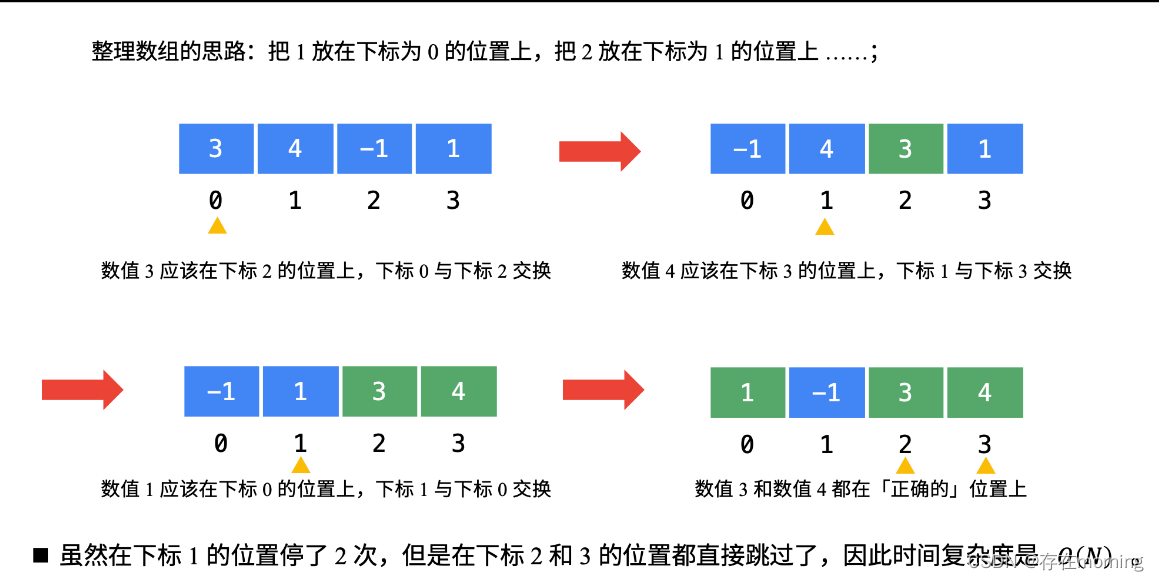
代码实现
给出代码实现基本档案
基本数据结构:数组
辅助数据结构:无
算法:迭代
技巧:双指针(逆序双指针)
其中数据结构、算法和技巧分别来自:
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
- 技巧:双指针、滑动窗口、中心扩散
当然包括但不限于以上
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*** @param nums int整型一维数组* @return int整型*/public int minNumberDisappeared (int[] nums) {// 原地hash:元素位置+1=元素值(i+1=nums[i]=>i=nums[i]-1),才满足各回各家,先将元素归位for (int i = 0; i < nums.length; i++) {while (nums[i] > 0 && nums[i] < nums.length && nums[i] != nums[nums[i] - 1]) {swap(nums, i, nums[i] - 1);}}// 遍历一遍数组,找到第一个不符合条件的返回for (int i = 0; i < nums.length; i++) {if (nums[i] != i+1) {return i + 1;}}return nums.length + 1;}// 交换元素位置private void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}
}
原地哈希就相当于,让每个数字n都回到下标为n-1的家里,那些没有回到家里的就成了流浪汉,他们要么是根本就没有自己的家(数字小于等于0或者大于nums.size()),要么是自己的家被别人占领了(出现了重复)。这些流浪汉被临时安置在下标为i的空房子里,之所以有空房子是因为房子i的主人i+1失踪了(数字i+1缺失)。因此通过原地构建哈希让各个数字回家,我们就可以找到原始数组中重复的数字还有消失的数字。
- 为什么内部是while循环,我们的目标是把
nums[i]在[1,N]范围内的数字归位,所以每个有家的流浪汉都要找到它的房子,i位置上的流浪汉找到了自己的房子nums[i]-1,但nums[i]-1房子被赶出来的流浪汉的房子却未必是i位置,它需要临时住在i并继续找自己的房子。所以直到nums[i]-1换回来的流浪汉正好对应i这个房子或这个流浪汉压根就没房子(非【1-N】范围的值),这次寻找才算结束 - 判断条件为什么有
nums[i] > 0 && nums[i] < nums.length,对于[7,8,9,10],这种数来说,因为不可能满足哈希映射条件,交换操作还会导致数组越界,所以没必要也不能进行移动;流浪汉压根没房子 - 判断条件为什么是
nums[i] != nums[nums[i] - 1]。因为对于[3,4,3,1],这种数来说,i!=nums[i]-1虽然满足条件,但是交换后因为还是[3,4,3,1],所以会导致一直交换死循环,所以要采取更严苛的判断条件避免重复元素交换,也就是交换位置上的数不能相同!而且值得注意的是满足nums[i] != nums[nums[i] - 1]其实就一定满足i!=nums[i]-1
复杂度分析
- 时间复杂度:O(N)。遍历了一遍数组,时间复杂度为O(N)
- 空间复杂度:O(1)。 需要建立长度为 m+n 的中间数组
相关文章:

【数据结构-哈希表 一】【原地哈希】:缺失的第一个正整数
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【原地哈希】,使用【数组】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&…...
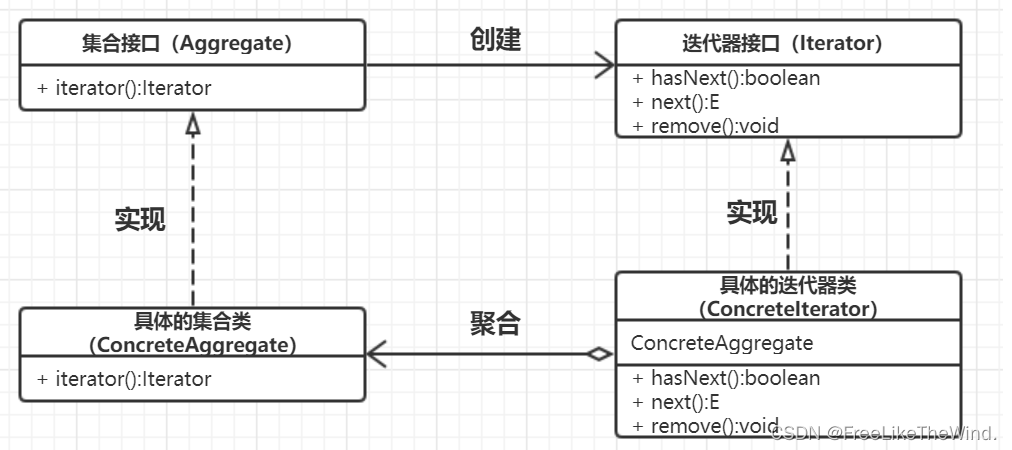
【C++设计模式之迭代器模式】分析及示例
简介 迭代器模式是一种行为型设计模式,它提供了一种顺序访问聚合对象元素的方法,而又不需要暴露聚合对象的内部结构。迭代器模式通过将遍历算法封装在迭代器对象中,可以使得遍历过程更简洁、灵活,并且符合开闭原则。 描述 迭代…...

【代码随想录】LC 27. 移除元素
文章目录 前言一、题目1、原题链接2、题目描述 二、解题报告1、思路分析2、时间复杂度3、代码详解 三、知识风暴 前言 本专栏文章为《代码随想录》书籍的刷题题解以及读书笔记,如有侵权,立即删除。 一、题目 1、原题链接 27. 移除元素 2、题目描述 二、…...
)
crash工具分析dma设备内存踩踏(一)
背景介绍 我们的客户在利用我们提供的SDK参考方案开发相关产品时,在产品方案上进行一些基础老化测试时,极低概率出现kernel随机panic问题,由于场景复杂,无法单独针对特定模块或功能进行拆解来进行实验排查,只能基于已…...
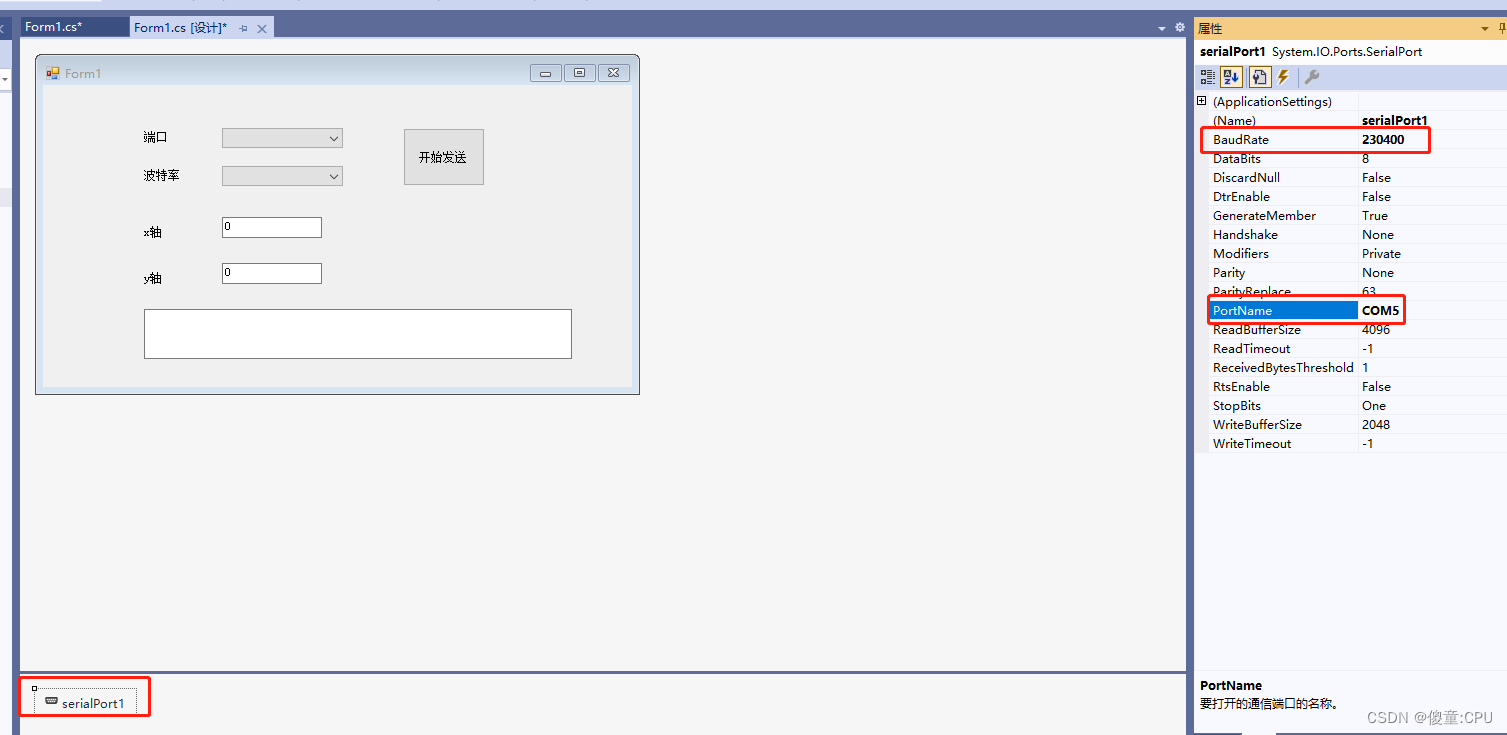
C#上位机——根据命令发送
C#上位机——根据命令发送 第一步:设置窗口的布局 第二步:设置各个属性 第三步:编写各个模块之间的关系...

BEVFormer代码跑通
1 环境配置 1.1 环境安装 # 1 拉取源码 github加速代理https://ghproxy.com/ git clone https://github.com/fundamentalvision/BEVFormer.git# 2 创建虚拟环境 conda create -n bev python3.8 -y# 3 激活虚拟环境 conda activate bev# 4.1 安装torch,torchvision,torchaud…...
kafka安装
kafka安装 1 kafka概念 1.1 kafka介绍 kafka是最初有Linkedin公司开发的,是一个分布式,分区,多副本,多生产者,多订阅者,基于zookeeper协调的分布式日志系统。具有高吞吐量,可扩展性和可容错性…...

Mac上安装Java的JDK多版本管理软件jEnv
JDK的多版本管理软件主要有以下三种: jEnv jEnv 是一个命令行工具,可以帮助您管理和切换不同版本的 Java 环境。它可以让您在不同的项目之间轻松切换 Java 版本。您可以使用 jenv global 命令设置全局 Java 版本,也可以使用 jenv local 命令…...

linux常见命令以及jdk,tomcat环境搭建
目录 Is pwd cd touch cat echo vim 复制粘贴 mkdir rm cp jdk部署 1. yum list | grep jdk进行查找编辑 2.安装编辑 3.再次确认 4.判断是否安装成功 tomcat安装 1.下载压缩包,把压缩包上传至linux(可能需要yum install lrzsz) 2.解压缩unzip 压缩包名&…...
将表情存入数据库
概念: 表情是一种比较特殊的字符串,为unicode编码,unicode编码要存入数据库一般情况下,是存不了的,有两种解决方式,一种将数据表编码方式改为unicode编码方式,但是这种情况适用于功能刚开始设计…...
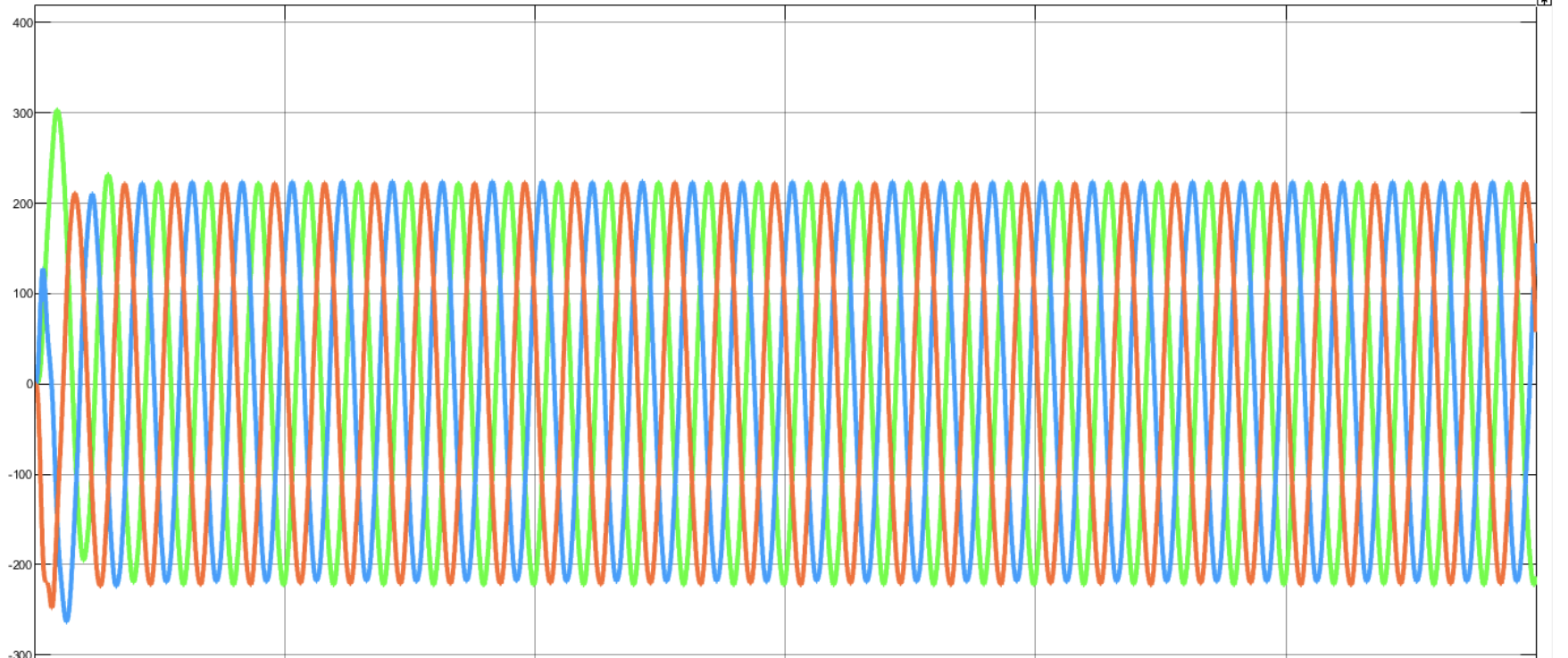
H桥级联型五电平三相逆变器Simulink仿真模型
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
后端解决跨域(极速版)
header(Access-Control-Allow-Origin: *); header(Access-Control-Allow-Methods:*); 代表接收全部的请求,"POST,GET"//允许访问的方式 指定域,如http://172.20.0.206//宝塔的域名,注意不是:http://wang.jingyi.icu等…...
数据结构与算法-前缀树
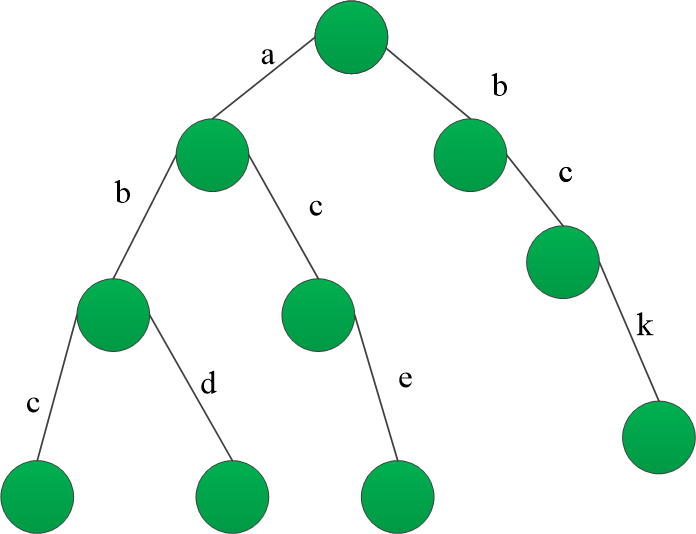
数据结构与算法-前缀树详解 1 何为前缀树 2 前缀树的代码表示及相关操作 1 何为前缀树 前缀树 又称之为字典树,是一种多路查找树,多路树形结构,是哈希树的变种,和hash效率有一拼,是一种用于快速检索的多叉树结构。 性质:不同字符串的相同…...
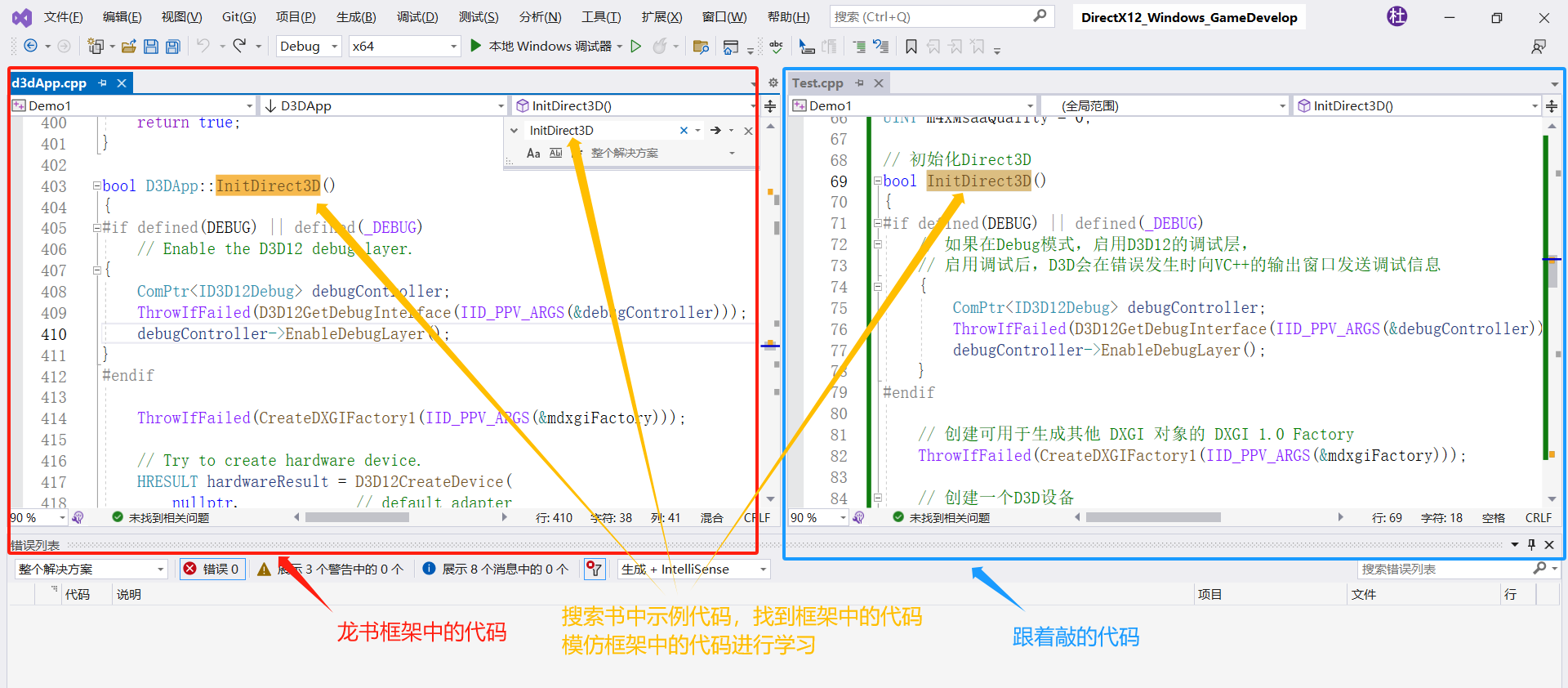
DirectX12_Windows_GameDevelop_3:Direct3D的初始化
引言 查看龙书时发现,第四章介绍预备知识的代码不太利于学习。因为它不像是LearnOpenGL那样从头开始一步一步教你敲代码,导致你没有一种整体感。如果你把它当作某一块的代码进行学习,你跟着敲会发现,总有几个变量是没有定义的。这…...
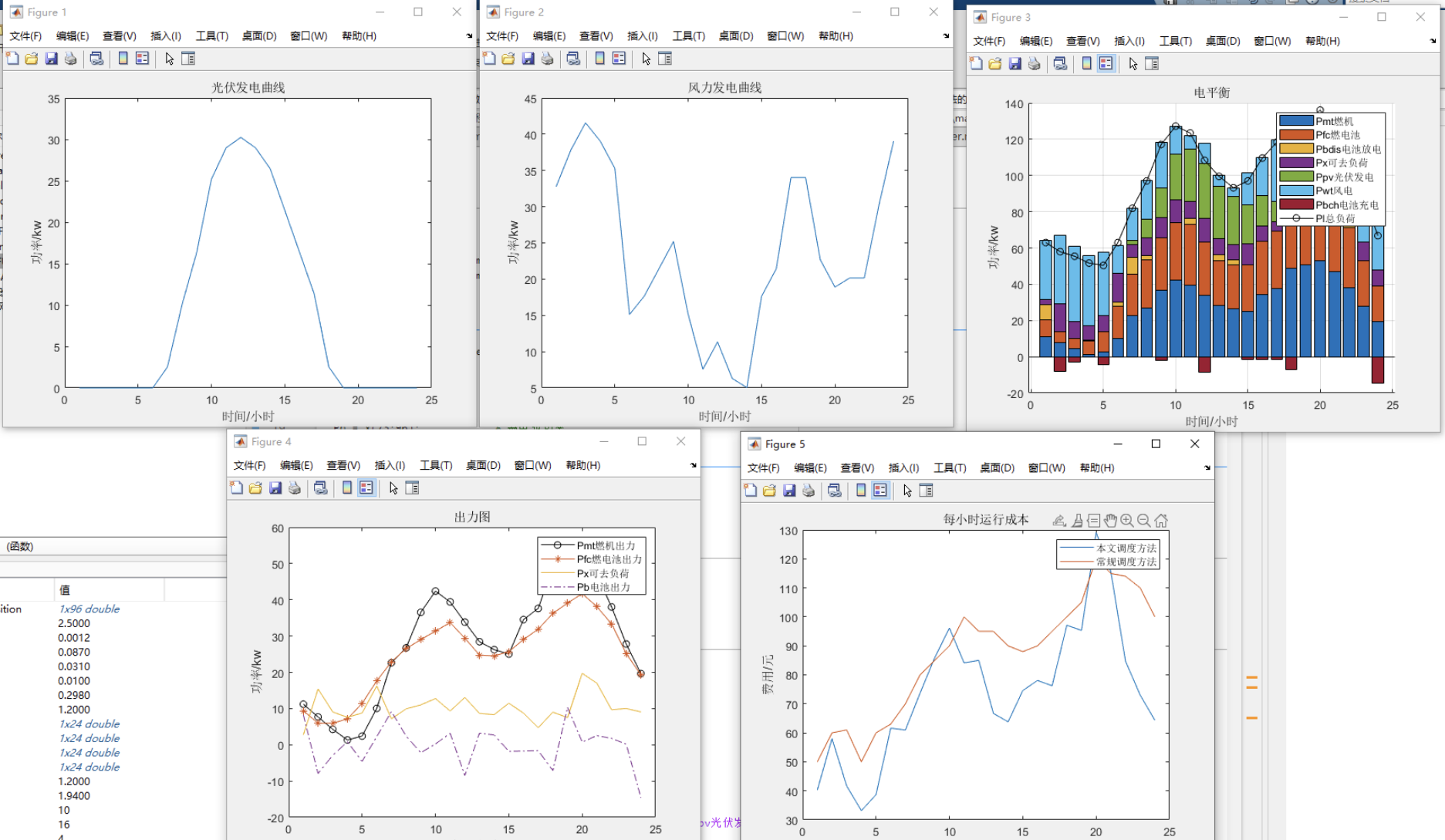
基于粒子群优化算法、鲸鱼算法、改进的淘沙骆驼模型算法(PSO/SSA/tGSSA)的微电网优化调度(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
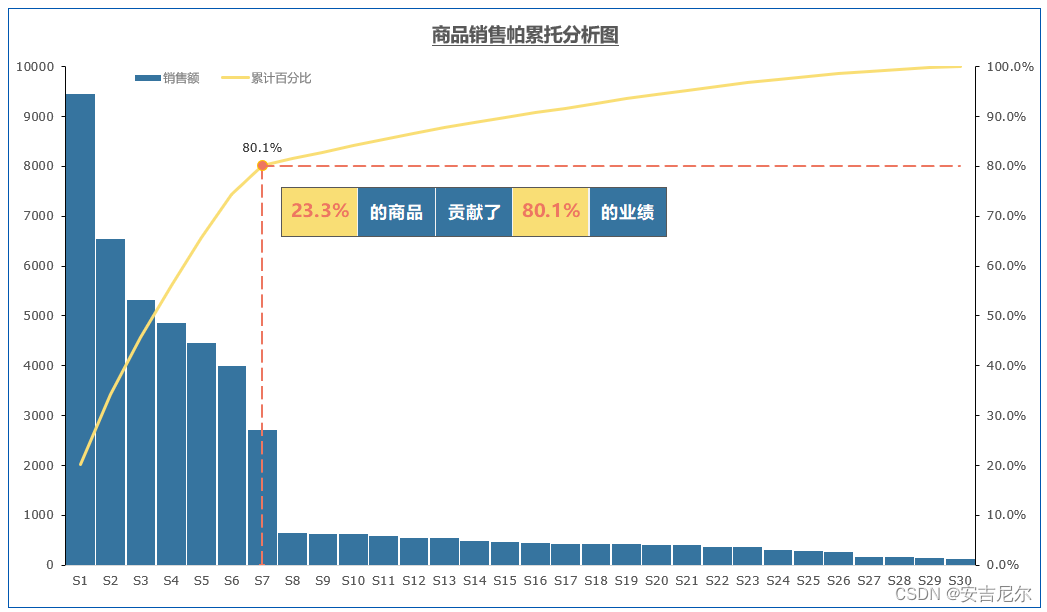
数据分析篇-数据认知分析
一简介 数据认知分析,实际是对数据的整体结构和分布特征进行分析,是对整个数据外在的认识,也是数据分析的第一步。对于数据认知的分析,一般会考虑分散性、位置特性、变量的相关性等,一般会考虑平均数、方差、极差、峰…...

【力扣-每日一题】714. 买卖股票的最佳时机含手续费
class Solution { public:int maxProfit(vector<int>& prices, int fee) {//[i][0]-不持有 [i][1]-持有int mprices.size();vector<vector<int>> dp(m,vector<int>(2));dp[0][0]0; //初始状态dp[0][1]-prices[0];for(int i1;i<m;i){dp[i]…...
【代码实践】HAT代码Window平台下运行实践记录
HAT是CVPR2023上的自然图像超分辨率重建论文《activating More Pixels in Image Super-Resolution Transformer》所提出的模型。本文旨在记录在Window系统下运行该官方代码(https://github.com/XPixelGroup/HAT)的过程,中间会遇到一些问题&am…...

机器学习-Pytorch基础
Numpy和Pytorch可以相互转换,前者CPU上,后者GPU上,都是对矩阵进行运算,Pytorch的基本单位是张量。torch 可以初始化全为0、全为1、符合正态分布的矩阵确定性初始化 torch.tensor()torch.arrange()torch.linspace()torch.logspace…...

金九银十,刷完这个笔记,17K不能再少了....
大家好,最近有不少小伙伴在后台留言,得准备面试了,又不知道从何下手!为了帮大家节约时间,特意准备了一份面试相关的资料,内容非常的全面,真的可以好好补一补,希望大家在都能拿到理想…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...
