Python数据攻略-Pandas与统计数据分析
相关文章:

Python数据攻略-Pandas与统计数据分析
统计学在数据分析中到底有多重要?在数据分析的世界里,统计学扮演着一角色。想象一下你是《三国志》游戏的数据分析师,任务是找出哪个武将最受玩家欢迎,哪些战役最具挑战性等。 你怎么做呢?这就需要统计学的力量了。 文章目录 基础统计方法描述性统计方差和标准差相关性和…...
【gcc】RtpTransportControllerSend学习笔记 1
本文是大神 https://www.cnblogs.com/ishen 的文章的学习笔记。主要是大神文章: webrtc源码分析(8)-拥塞控制(上)-码率预估 的学习笔记。大神的webrtc源码分析(8)-拥塞控制(上)-码率预估 详尽而具体,堪称神作。因为直接看大神的文章,自己啥也没记住,所以同时跟着看代码。跟…...

若依分离版-前端使用
1 执行 npm install --registryhttps://registry.npm.taobao.org,报错信息如下 npm ERR! code ERESOLVE npm ERR! ERESOLVE unable to resolve dependency tree npm ERR! npm ERR! While resolving: ktg-mes-ui3.8.2 npm ERR! Found: vue2.6.12 npm ERR! node_modu…...

微信小程序-2
微信开发文档 https://developers.weixin.qq.com/miniprogram/dev/framework/ 一、app.js中的生命周期函数与globalData(全局变量) 指南 - - - 小程序框架 - - - 注册小程序 删除app.js里的东西,输入App回车,调用生命周期 选项 - - - 重新打开此项目…...
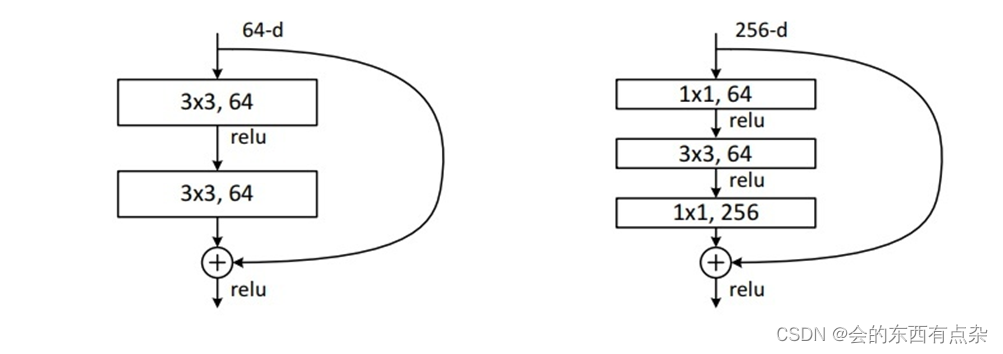
卷积神经网络的发展历史-ResNet
ResNet的产生 2015 年,Kaiming He 提出了ResNet(拿到了 2016 年 CVPR Best Paper Award),不仅解决了神经网络中的退化问题还在同年的ILSVRC和COCO 竞赛横扫竞争对手,分别拿下分类、定位、检测、分割任务的第一名。 R…...
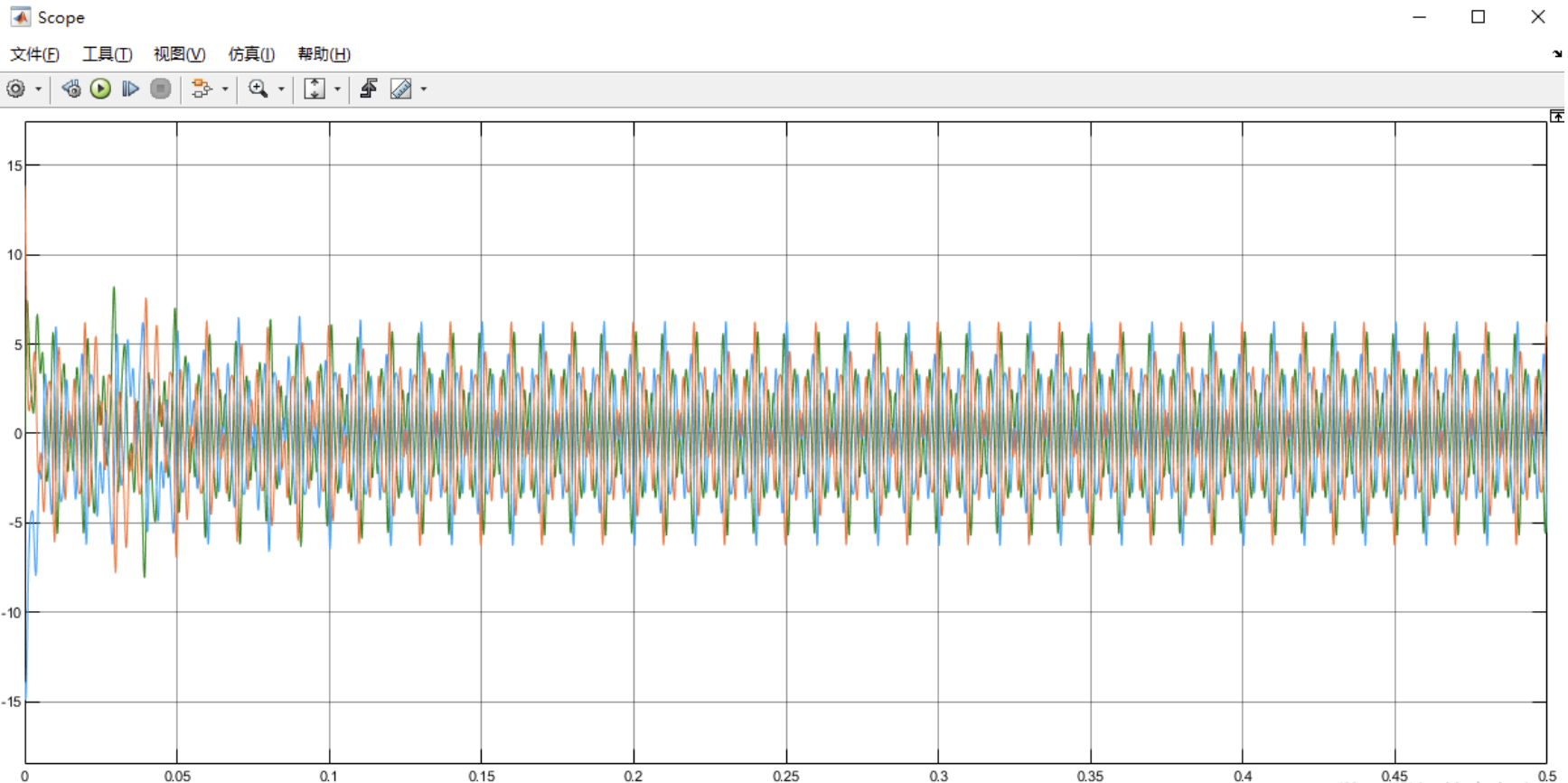
基于瞬时无功功率ip-iq的谐波信号检测Simulink仿真
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

node安装,nvm管理器
一、下载nvm,nvm-setup.exe https://github.com/coreybutler/nvm-windows/releases 二、配置NodeJS下载代理镜像(可选) 可以在NVM安装根目录下的setting.txt文件中,配置NodeJS下载代理镜像,解决在线安装NodeJS时速度…...
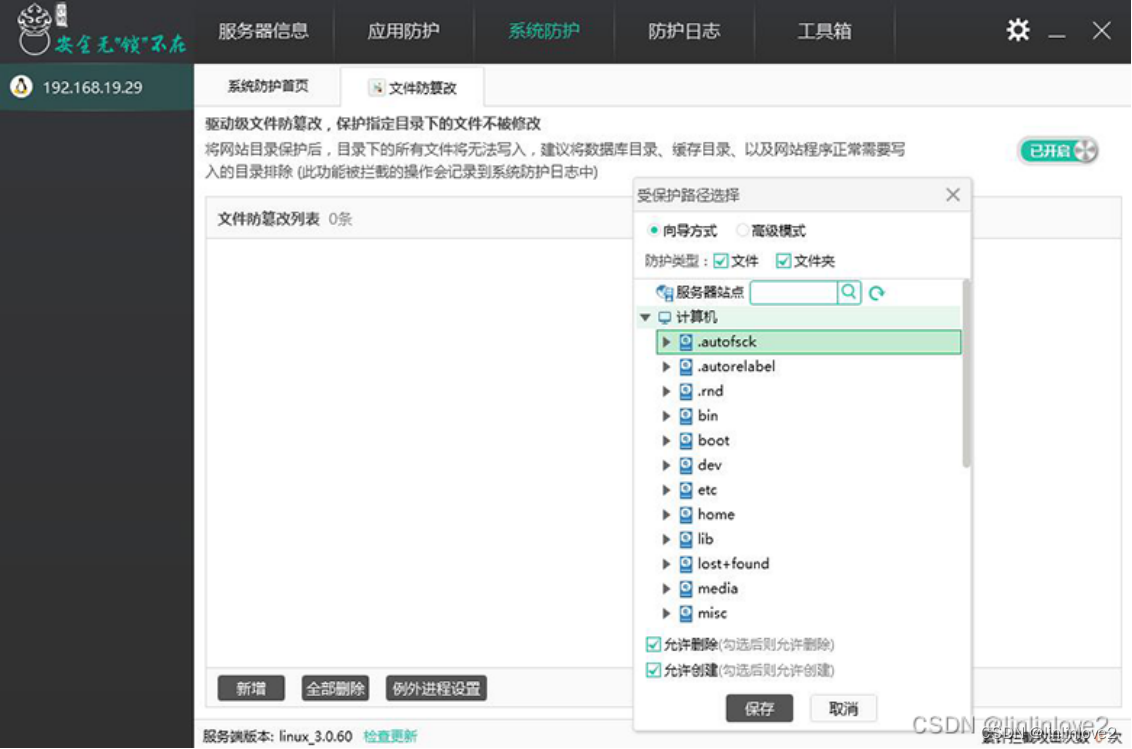
华为云云耀云服务器L实例评测|Ubuntu云锁防火墙安装搭建使用
华为云云耀云服务器L实例评测|Ubuntu安装云锁防火墙对抗服务器入侵和网络攻击 1.前言概述 华为云耀云服务器L实例是新一代开箱即用、面向中小企业和开发者打造的全新轻量应用云服务器。多种产品规格,满足您对成本、性能及技术创新的诉求。云耀云服务器L…...
C# OpenCvSharp 实现迷宫解密
效果 项目 代码 using OpenCvSharp; using System; using System.Drawing; using System.Windows.Forms;namespace OpenCvSharp_实现迷宫解密 {public partial class Form1 : Form{public Form1(){InitializeComponent();}private void Form1_Load(object sender, EventArgs e…...
趣味工具箱小程序源码
趣味工具箱小程序源码,支持功能去水印,精选壁纸,图片压缩,文字生成二维码,图片加水印,模拟来电,手持弹幕,掷骰子…等 使用小工具,一个小程序有几十个功能。 源码下载&am…...

互联网Java工程师面试题·Redis 篇·第二弹
目录 16、Redis 集群方案什么情况下会导致整个集群不可用? 17、Redis 支持的 Java 客户端都有哪些?官方推荐用哪个? 18、Jedis 与 Redisson 对比有什么优缺点? 19、Redis 如何设置密码及验证密码? 20、说说 Redis…...
)
FreeRTOS入门教程(信号量的概念及API函数使用)
文章目录 前言一、什么是信号量二、信号量种类和对比三、信号量和队列的区别四、信号量相关的函数1.创建函数2.删除函数3.获取和释放信号量函数 总结 前言 本篇文章正式带大家开始学习什么是信号量,并且掌握信号量函数的基本使用方法,并且将和队列进行一…...
简易版Pycharm(2023)+Conda开发环境配置教程
困 扰 不知道为什么,自从Pycharm更新了新的版本以后,在Pycharm中为项目工程配置Python解释器环境时,总是不能像以前那么方便的配置。 比如,当前Conda中有十个不同的开发环境,每个环境一个名称,比如&#x…...
深入浅出,SpringBoot整合Quartz实现定时任务与Redis健康检测(二)
前言 在上一篇深入浅出,SpringBoot整合Quartz实现定时任务与Redis健康检测(一)_往事如烟隔多年的博客-CSDN博客 文章中对SpringBoot整合Quartz做了初步的介绍以及提供了一个基本的使用例子,因为实际各自的需求任务不尽相同因此并…...
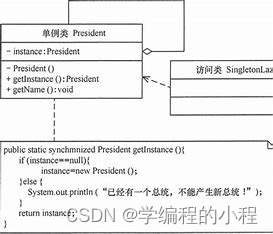
小谈设计模式(22)—单例模式
小谈设计模式(22)—单例模式 专栏介绍专栏地址专栏介绍 单例模式点睛所在优缺点分析优点确保只有一个实例全局访问点节省资源线程安全 缺点难以扩展对象的生命周期单一职责原则隐藏依赖关系 Java程序实例实例a分析实例b,更安全分析优化 ——“…...

华为OD机考算法题:分班
题目部分 题目分班难度易题目说明幼儿园两个班的小朋友在排队时混在了一起,每位小朋友都知道自己是否与前面一位小朋友是否同班,请你帮忙把同班的小朋友找出来。 小朋友的编号为整数,与前一位小朋友同班用 Y 表示,不同班用 N 表示…...

【gcc】RtpTransportControllerSend学习笔记 3:gcc
本文是大神 https://www.cnblogs.com/ishen 的文章的学习笔记。大神的webrtc源码分析(8)-拥塞控制(上)-码率预估 详尽而具体,堪称神作。本文使用的代码是m79 ,与大神有不同。2.4 Probe只会在一些特殊的时候才会进行探测(链路刚开始时, 码率不正常暴跌时)2.5 : 对发送的吞吐量…...
CSP-J第二轮试题-2019年-3题
文章目录 参考:总结 [CSP-J2019] 纪念品题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 样例 #2样例输入 #2样例输出 #2 提示答案 现场真题注意事项 参考: P5662 CSP-J2019纪念品 总结 本系列为CSP-J/S算法竞赛真题讲解,会按照年…...
)
数据库:Hive转Presto(三)
继续上节代码。 import re import os import tkinter.filedialog from tkinter import *class Hive2Presto:def __int__(self):self.t_funcs [substr, nvl, substring, unix_timestamp] \[to_date, concat, sum, avg, abs, year, month, ceiling, floor]self.time_funcs [d…...

【AI视野·今日Robot 机器人论文速览 第四十八期】Thu, 5 Oct 2023
AI视野今日CS.Robotics 机器人学论文速览 Thu, 5 Oct 2023 Totally 32 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers LanguageMPC: Large Language Models as Decision Makers for Autonomous Driving Authors Hao Sha, Yao Mu, Yuxuan Jiang, Li…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
