力扣第257题 二叉树的所有路径 c++ 树 深度优先搜索 字符串 回溯 二叉树
题目
257. 二叉树的所有路径
简单
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
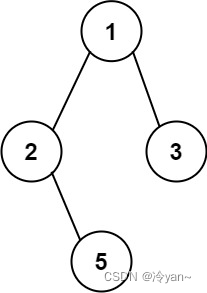
输入:root = [1,2,3,null,5] 输出:["1->2->5","1->3"]
示例 2:
输入:root = [1] 输出:["1"]
提示:
- 树中节点的数目在范围
[1, 100]内 -100 <= Node.val <= 100
思路和解题方法
1. 首先我们需要明确这个问题的目标,即找到所有从根节点到叶节点的路径。对于每一条路径,我们需要把其中的每个节点的值按顺序连接起来形成一个字符串,并将其保存在一个字符串数组中返回。
2. 通过观察代码,我们可以发现该题解中使用了递归的思想来解决问题。具体来说,它定义了一个名为
traversal的递归函数,该函数需要传入三个参数:
node: 当前访问的节点。path: 保存当前路径的节点值的数组。ans: 保存所有路径的字符串的数组。3. 对于每个节点
node,该函数首先将node->val添加到path中,并判断node是否为叶节点(即node->left==NULL&&node->right==NULL),如果是,则将path中的所有值按顺序连接起来形成一个字符串,并将其添加到ans数组中;否则,递归遍历node的左右子树,并在递归返回后将path数组中的最后一个元素弹出,以恢复到上一层递归时的状态。4. 最终,在主函数
binaryTreePaths中,我们首先判断根节点是否为空,如果为空,则返回空的字符串数组;否则,我们调用traversal函数,将根节点、空的path数组和空的ans数组作为参数传入,以获取所有路径。最后,返回ans数组即可。
复杂度
时间复杂度:
O(n)
时间复杂度:对于每个节点,我们只需要访问一次,其中 n 是节点数。
空间复杂度
O(n)
递归过程中使用了一个字符串类型的参数
path和一个字符串数组ans,以及递归调用栈,因此空间复杂度为 O(n)。特别地,如果所有的节点都在同一条路径上,递归栈的最大深度将是 n,在这种情况下,空间复杂度将达到 O(n) 的最坏情况。
c++ 代码
class Solution {
public:// 辅助函数,用于递归遍历二叉树并找到所有路径void traversal(TreeNode* node, vector<int>& path, vector<string>& ans) {// 将当前节点的值添加到路径中path.push_back(node->val);// 如果当前节点是叶节点,则将路径转化为字符串,并添加到结果数组中if (node->left == nullptr && node->right == nullptr) {string sPath; // 储存当前路径的字符串形式for (int i = 0; i < path.size() - 1; i++) {sPath += to_string(path[i]); // 将路径节点的值转化为字符串并添加到路径字符串中sPath += "->"; // 添加箭头符号分隔路径节点}sPath += to_string(path[path.size() - 1]); // 添加最后一个节点的值ans.push_back(sPath); // 将路径字符串添加到结果数组中return;}// 递归遍历左子树if (node->left) {traversal(node->left, path, ans);path.pop_back(); // 返回上一层递归之前,弹出当前节点,恢复路径状态}// 递归遍历右子树if (node->right) {traversal(node->right, path, ans);path.pop_back(); // 返回上一层递归之前,弹出当前节点,恢复路径状态}}vector<string> binaryTreePaths(TreeNode* root) {vector<int> path; // 用于保存当前路径节点的值的数组vector<string> ans; // 用于保存所有路径字符串的数组if (root == nullptr) return ans; // 特殊情况处理,空树直接返回空结果数组traversal(root, path, ans); // 递归遍历二叉树,找到所有路径return ans; // 返回结果数组}
};
c++优化代码 (精简)
class Solution {
public:// 辅助函数,用于递归遍历二叉树并找到所有路径void traversal(TreeNode* node, string path, vector<string>& ans) {// 如果节点为空,直接返回if (node == nullptr) return;// 将当前节点的值添加到路径中path += to_string(node->val);// 如果当前节点是叶节点,则将完整路径添加到结果数组中if (node->left == nullptr && node->right == nullptr) {ans.push_back(path);return;}// 添加箭头符号分隔路径节点path += "->";// 递归遍历左子树traversal(node->left, path, ans);// 递归遍历右子树traversal(node->right, path, ans);}vector<string> binaryTreePaths(TreeNode* root) {vector<string> ans; // 用于保存所有路径的数组traversal(root, "", ans); // 递归遍历二叉树,找到所有路径return ans; // 返回结果数组}
};
对
traversal函数进行了修改。我们使用一个额外的string类型的参数path来保存当前路径的字符串而不是使用一个整数数组。在递归过程中,我们将当前节点的值加入到
path结尾,并根据情况添加箭头符号"->"。此外,我们还对参数进行了一些调整,使用
nullptr表示空指针,而不是NULL。这是 C++11 引入的nullptr关键字,它更为直观和安全。
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
相关文章:

力扣第257题 二叉树的所有路径 c++ 树 深度优先搜索 字符串 回溯 二叉树
题目 257. 二叉树的所有路径 简单 给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。 叶子节点 是指没有子节点的节点。 示例 1: 输入:root [1,2,3,null,5] 输出:["1->2-&g…...

保研之旅·终
一.背景 学校: 中211 通信工程专业 成绩: 绩点前3% 英语: CET4:523 CET6:505 竞赛:两个国奖,若干省奖 科研:两项校级大创,无论文产出 二.基本情况 夏令营入营: 哈工大…...

达梦数据库 视图 错误 [22003]: 数据溢出
今天通过DBeaver连接访问达梦数据库的一个视图,报错:错误 [22003]: 数据溢出 经过分析,原因是视图字段的数据类型和原表的数据类型不一致造成的...

【文献阅读】【NMI 2022】LocalTransform :基于广义模板的有机反应性准确预测图神经网络
预测有机反应产物是有机化学的一个基本问题。基于成熟有机化学知识,化学家现在能够设计实验来制造用于不同目的的新分子。但是,它需要经验丰富的专业化学家来准确预测化学反应的结果。为了进一步帮助有机化学家并在数字化学时代实现全自动发现࿰…...

QQ浏览器怎么才能设置默认搜索引擎为百度
问题: 打开QQ浏览器,搜索相关信息时发现总是默认为”搜狗搜索引擎“,想将其转为”百度搜索引擎“ 解决: 1、点击浏览器右侧”菜单“图标,选择”设置“,如下图所示: 2、在”常规设置“中的”搜…...

Go Gin Gorm Casbin权限管理实现 - 3. 实现Gin鉴权中间件
文章目录 0. 背景1. 准备工作2. gin中间件2.1 中间件代码2.2 中间件使用2.3 测试中间件使用结果 3. 添加权限管理API3.1 获取所有用户3.2 获取所有角色组3.3 获取所有角色组的策略3.4 修改角色组策略3.5 删除角色组策略3.6 添加用户到组3.7 从组中删除用户3.8 测试API 4. 最终目…...

js 封装一个异步任务函数
// 异步任务 封装 // 1,定义函数 // 2,使用核心api(queueMicrotask,MutationObserver,setTimeout) function runAsynctask (callback){if(typeof queueMicrotask "function" ){queueMicrotask(callback)}else if( typeof MutationObserver "functio…...

目标检测YOLO实战应用案例100讲-基于无人机航拍图像的目标检测
目录 前言 国内外研究现状 目标检测研究现状 无人机航拍目标检测研究现状...
PyQt5配置踩坑
安装步骤比较简单,这里只说一下我踩的坑,以及希望一些大佬可以给点建议。 一、QtDesigner 这个配置比较简单,直接就能用,我的配置如下图: C:\Users\lenovo\AppData\Roaming\Python\Python311\site-packages\qt5_app…...
内网渗透笔记之内网基础知识
0x01 内网概述 内网也指局域网(Local Area Network,LAN)是指在某一区域内由多台计算机互联成的计算机组。一般是方圆几千米以内。局域网可以实现文件管理、应用软件共享、打印机共享、工作组内的历程安排、电子邮件和传真通信服务等功能。 内…...
vue3+elementPlus:el-select选择器里添加按钮button
vue3elementPlus:el-select选择器里添加按钮button,在el-select的option后面添加button //html <el-select class"selectIcon" value-key"id" v-model"store.state.HeaderfilterText" multiple collapse-tagscollapse-…...

Android 模拟点击
Android 模拟点击 1.通过代码的方式实现 通过模拟MotionEvent的方式实现 //----------------模拟点击--------------------- private void simulateClick(View view, float x, float y) {long downTime SystemClock.uptimeMillis();final MotionEvent downEvent MotionEve…...

css自学框架之选项卡
这一节我们学习切换选项卡,两种切换方式,一种是单击切换选项,一种是鼠标滑动切换,通过参数来控制,切换方法。 一、参数 属性默认值描述tabBar.myth-tab-header span鼠标触发区域tabCon.myth-tab-content主体区域cla…...

Element Plus组件库中的input组件如何点击查看按钮时不可编辑,点击编辑时可编辑使用setup
如果你正在使用 Vue 3 和 Composition API,你可以使用 setup 函数来实现 Element Plus 的 Input 组件在点击查看按钮时不可编辑,点击编辑按钮时可编辑的功能。 以下是一个使用 setup 的示例代码: <template><div><el-input …...
小米、华为、iPhone、OPPO、vivo如何在手机让几张图拼成一张?
现在很多手机自带的相册APP已经有这个拼图功能了。 华为手机的拼图 打开图库,选定需要拼图的几张图片后,点击底部的【创作】,然后选择【拼图】就可以将多张图片按照自己想要的位置,组合在一起。 OPPO手机的拼图 打开相册&#…...

物联网AI MicroPython传感器学习 之 WS2812 RGB点阵灯环
学物联网,来万物简单IoT物联网!! 一、产品简介 ws2812是一个集控制电路与发光电路于一体的智能外控LED光源。其外型与一个5050LED灯珠相同,每个元件即为一个像素点。像素点内部包含了智能数字接口数据锁存信号整形放大驱动电路&a…...

【GPU常见概念】GPU常见概念及分类简述
随着大模型和人工智能的爆火,大家对GPU的关注持续上升,本文简单简述下GPU经常用的概念。 GPU(图形处理器),又称显示核心、视觉处理器、显示芯片,是一种专门在个人电脑、工作站、游戏机和一些移动设备&…...
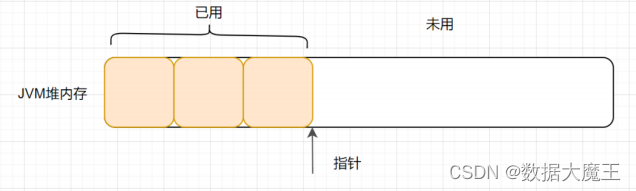
JVM篇---第九篇
系列文章目录 文章目录 系列文章目录一、什么是指针碰撞?二、什么是空闲列表三、什么是TLAB? 一、什么是指针碰撞? 一般情况下,JVM的对象都放在堆内存中(发生逃逸分析除外)。当类加载检查通过后࿰…...

探索 GAN 和 VAE 之外的 NLP 扩散模型
介绍 扩散模型最近引起了极大的关注,特别是在自然语言处理(NLP)领域。基于通过数据扩散噪声的概念,这些模型在各种NLP任务中表现出了卓越的能力。在本文中,我们将深入研究扩散模型,了解其基本原理,并探讨实际应用、优势、计算注意事项、扩散模型在多模态数据处理中的相…...

发现很多人分不清 jwt session token 的区别?
1. JWT(JSON Web Token) 1.1 什么是JWT? JWT,全称为JSON Web Token,是一种用于在网络上安全传输信息的开放标准。它的设计初衷是用于跨域通信,在不同域之间传递声明性信息。JWT是一种自包含的令牌&#x…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
