安全性算法

目录
一、安全性算法
二、基础术语
三、对称加密与非对称加密
四、数字签名
五、 哈希算法
六、哈希算法碰撞与溢出处理
一、安全性算法
安全性算法的必要性:
安全性算法的必要性是因为在现代数字化社会中,我们经常需要传输、存储和处理敏感的数据,如个人隐私信息、金融数据、商业机密等。这些数据如果未经过适当的保护,可能会被恶意攻击者获取、篡改或滥用。
安全性算法遵循以下四个特性
-
保密性(Confidentiality):确保只有授权者才能访问和查看数据,对非授权人员保持数据保密。
-
完整性(Integrity):确保数据在传输和存储过程中没有被篡改、损坏或破坏,保持数据的完整性和一致性。
-
认证性(Authentication):确认数据的来源和真实性,确保数据发送者和接收者的身份是真实的,并且数据没有被冒充或伪造。
-
不可否认性(Non-Repudiation):确保数据的发送者不能否认他/她发送过的数据,防止他/她在后期否认该数据的发送或者执行。
二、基础术语
| 概念 | 定义 |
|---|---|
| 明文 | 未经过加密处理的原始数据或信息。 |
| 密钥 | 用来进行加密和解密的一串字符或数字,只有持有相应密钥的人才能对加密数据进行解密。 |
| 密文 | 加密明文后的数据或信息。 |
| 私钥 | 用于非对称加密算法的一种密钥,只有私钥持有者才能进行解密。 |
| 公钥 | 用于非对称加密算法的一种密钥,公钥可以公开给任何人使用,但只有私钥持有者才能进行解密。 |
| 加密函数 | 一种算法,将明文和密钥作为输入,生成密文作为输出,实现对数据的保护。 |
| 解密函数 | 一种算法,将密文和密钥作为输入,生成明文作为输出,实现对加密数据的还原。 |
三、对称加密与非对称加密
1.对称加密
对称加密是一种加密技术,使用相同的密钥(也称为对称密钥)进行加密和解密。在对称加密算法中,发送方使用密钥将明文转换为密文,接收方使用相同的密钥将密文转换回明文。
对称加密的优点是加密和解密速度快,适用于大量数据的加密和解密操作。常见的对称加密算法有DES(数据加密标准)、AES(高级加密标准)等。
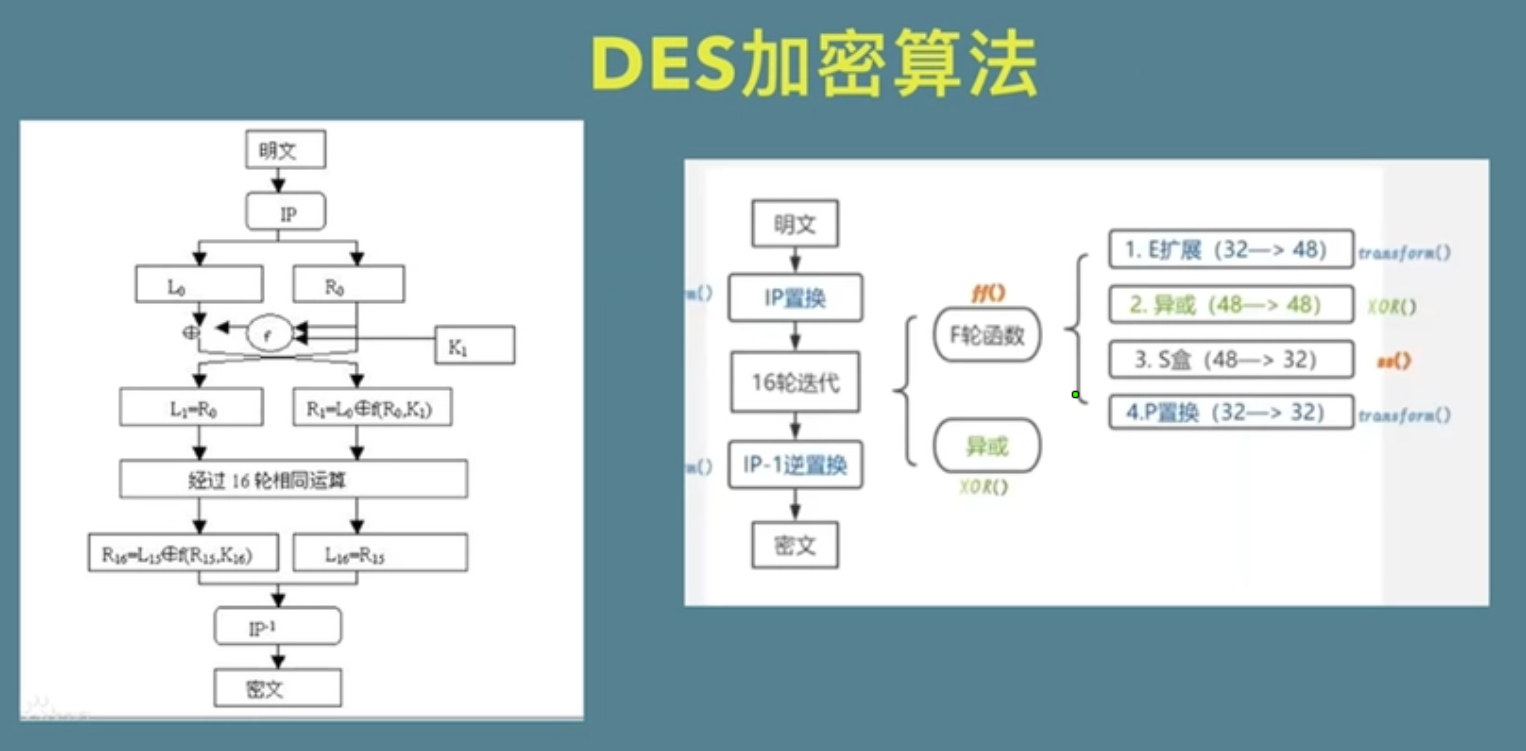
优点: 加密和解密速度快,适用于大量数据的加密和解密操作。常见的对称加密算法有DES(数据加密标准)、AES(高级加密标准)等。然而,对称加密存在一个问题,即如何安全地共享密钥。如果密钥在传输过程中被攻击者获取,那么加密的安全性就会被破坏。因此,在某些情况下,非对称加密算法更常被用于密钥的安全交换。
2.非对称加密
非对称加密是一种加密技术,与对称加密算法不同,它使用一对密钥进行加密和解密操作。这对密钥包括公钥(public key)和私钥(private key)。公钥可以公开给其他人使用,而私钥则只能由密钥的所有者保管,不公开给他人。
在非对称加密中,发送方使用接收方的公钥来加密数据,而接收方则使用自己的私钥来解密。相反,如果发送方要发送加密的信息给接收方,发送方可以使用自己的私钥进行签名,接收方使用发送方的公钥验证签名的有效性。这种加密和解密操作过程使用不同的密钥,因此被称为“非对称”。
常用非对称加密RSA
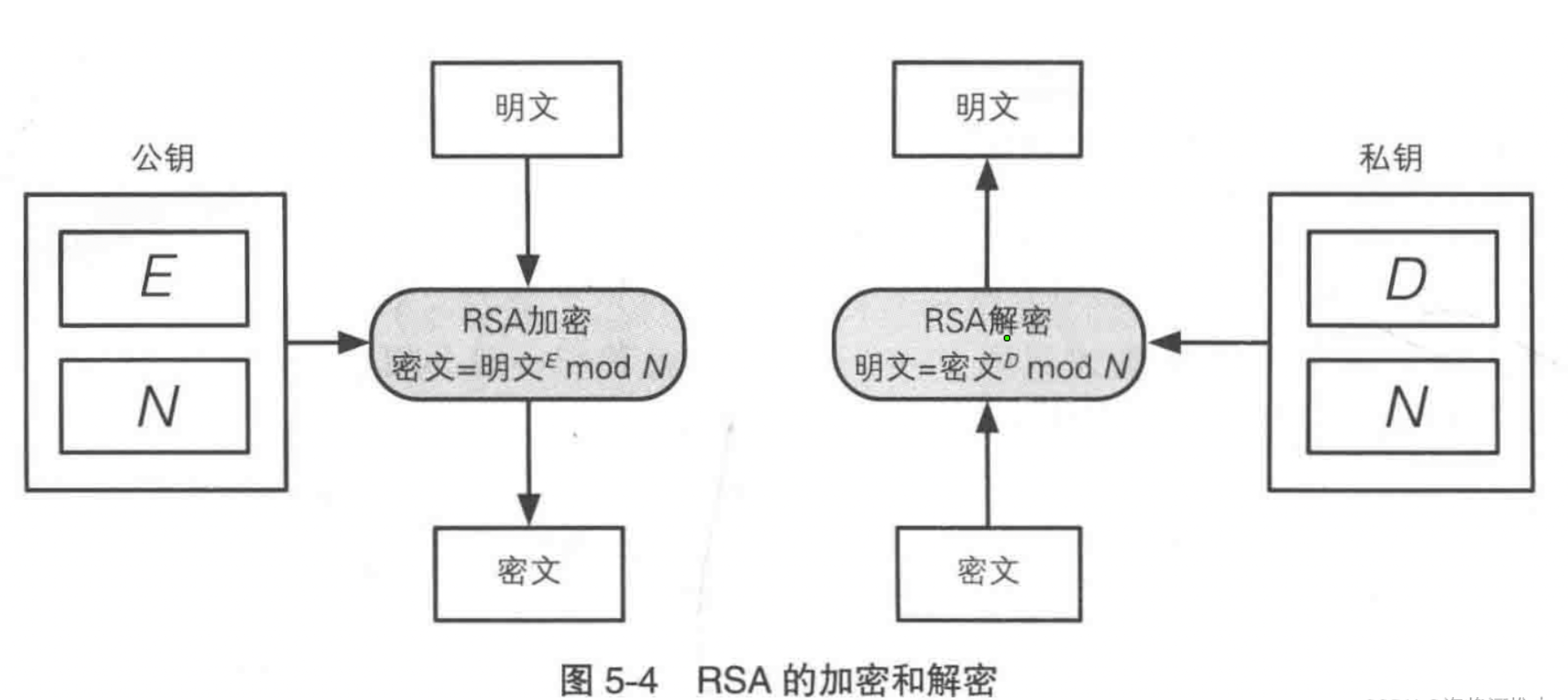
优点: 可以实现加密和解密的分离,并且可以安全地共享公钥。即使公钥被其他人获取,也无法通过公钥推导出私钥。常见的非对称加密算法有RSA(由Rivest、Shamir和Adleman发明)和Elliptic Curve Cryptography(椭圆曲线加密)等。
四、数字签名
1.数字签名概念
数字签名是一种用于验证数据完整性、身份认证和防止数据篡改的加密技术。它常用于确保发送方的身份,以及确保数据在传输过程中没有被篡改或伪造。
2.数字签名工作方式
数字签名的工作方式是以公钥和哈希函数相互配合使用的,用户A先将明文的M以哈希函数计算出哈希值H,再用自己的私钥对哈希值H进行加密,加密后的内容和即为"数字签名"。最后将明文与数字签名一起发送给用户B。由于这个数字签名是由用户A的私钥进行加密的,且该私钥只有A才有,因此该数字签名可以代表A的身份。
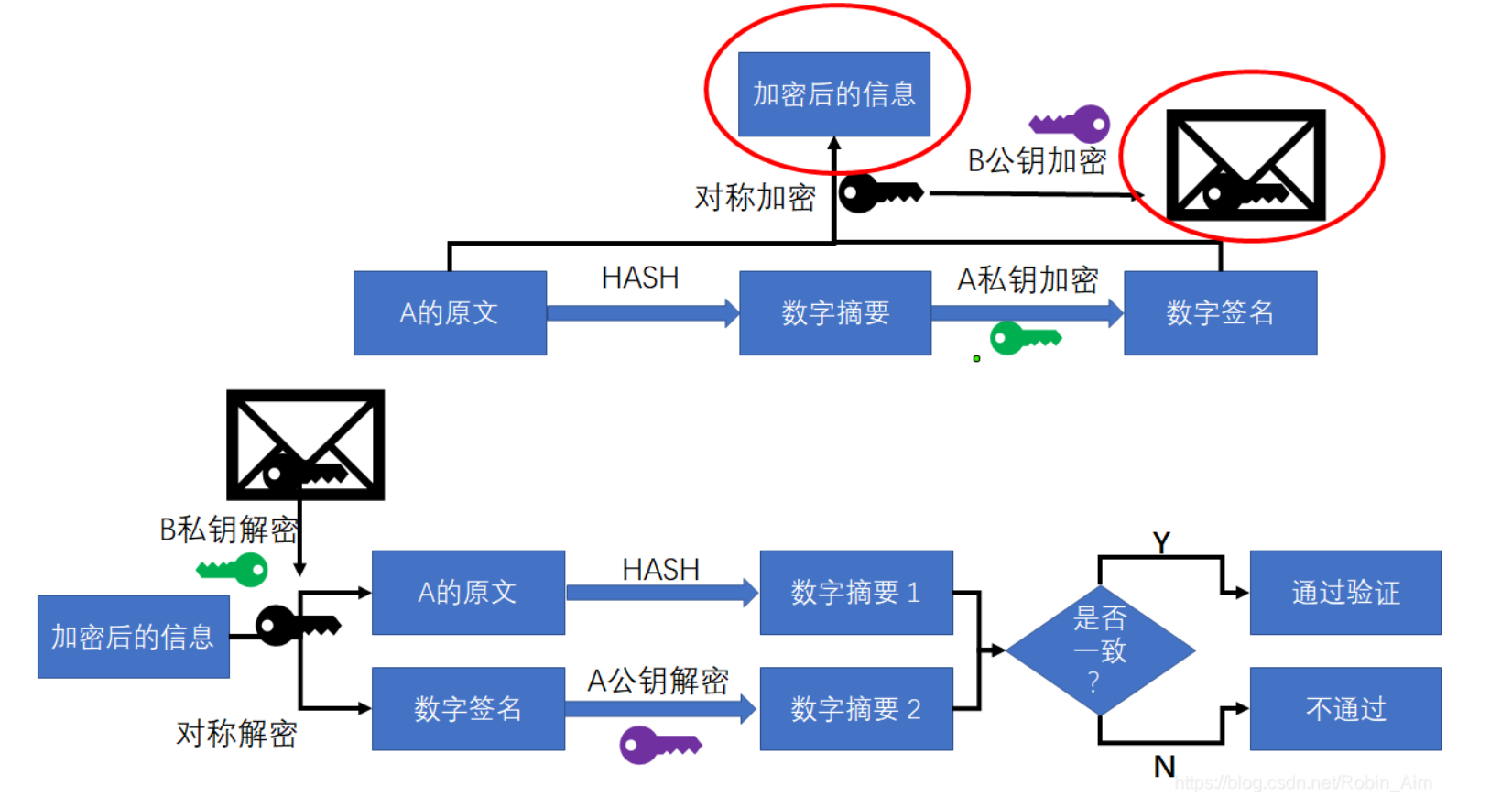
五、 哈希算法
1.哈希算法是通过哈希函数计算一个键值对应的地址,进而建立哈希表,并依靠哈希函数查找各个键值存放在哈希表中的地址。查找速度与数据的多少无关,在没有碰撞和数据溢出的情况下即可查找成功,该方法还有保密性高的特点。
常见的哈希算法有除留余数法,平方取中法,折叠法和数字分析法
1.除留余数法
最简单的哈希函数是将数据除以一个某个常数后,取余数作为索引。
h(key) = key mod B
案例:在一个有13个位置的数组中,只是用7个地址,值分别是12,65,70,99,33,67,48。那么B就可以是13 。
案例代码:
public class javaDemo {public static void main(String[] args) {Map<Integer,Integer> map = new HashMap<>();int data[] = new int[]{12,65,70,99,33,67,48};//初始化哈希表for (int i=0;i<13;i++){map.put(i,null);}//除留余数for (int temp:data) {map.put((temp%13),temp);}System.out.println(map);
//注意:改代码只是展示除留余数法,碰撞问题将在后面进行修改}
}
注意:B虽然可以自己定义,但是尽量选择用质数(除了1和自身外没有其他正因数的数)
2.平方取中法
平方取中法和除留余数法相当类似,就是先计算数据的平方,之后取中间的某段数字作为索引。
案例:
原始数据:12,65,70,99,33,67,51
平方后:144,4225,9801,1089,4489,2601
再通过取百位数或者十位数作为键值,取值后如下。
14,22,90,80,08,48,60
将上述7个数字对应原来的七个原始数据(12,65,70,99,33,67,51)
如果存放的空间为100地址空间
则正常进行数据映射如
f(14) = 12
f(22) = 65
.....
如果存放的空间为10地址空间,则需要对取值后的数进行压缩10倍,即14/10 = 1,22/10=2...
f(1) = 12
f(2) = 65
........
3.折叠法
折叠法是将数据转换为一串数字后,先将这串数字拆成及部分,再把他们加起来,就可以计算出这个键值的桶地址(Bucket Address),例如,有一个数据转换成数字后为2365479125443.若以每四个数字为一个部分,则可以拆分成2365、4791、2544、3.将这4组数字加起来后即为索引值。
2365+4791+2544+3 = 9703 ->桶地址
在折叠法中有两种做法。一种是向上例那样直接将每一部分相加所得的值作为其桶地址,这种做法成为“移动折叠法”。哈希法的设计原则之一是降低碰撞,如果希望降低碰撞,就可以将上述的数字中的技术为段或偶数位段反转后相加,以取得桶地址,这种改进后的做法成为“边界折叠法”
还是以上面的数字为例,请看下列说明
情况一:将偶数位段反转
2365(第一位的是奇数位,故不反转)
+1974(第二位的是偶数位,故要反转)
+ 2544(第三位的是奇数位,故不反转)
+ 3 (第四位的是偶数位,故要反转)
= 6886 ->桶地址
情况二:将奇数位段反转
5632 (第一位的是奇数位,需要反转)
+ 4791(第二位的是偶数位,故不反转)
+ 4452(第三位的是奇数位,需要反转)
+ 3 (第四位的是偶数位,故不反转)
= 14878 -> 桶地址
4.数字分析法
数字分析法,通过分析数据,找取数据中数字重复率低的数字,将索引空间放在数据中重复率最低的位置,以此作为数据的索引。
六、哈希算法碰撞与溢出处理
碰撞与溢出
哈希算法将输入数据映射到固定长度的哈希值。碰撞是指不同的输入数据最终得到相同的哈希值,而溢出则是指较大的输入数据映射到较小的输出空间中。这些问题的出现是由于哈希算法必须处理无限输入空间映射到有限输出空间的情况导致的。虽然设计者会尽力减少碰撞和溢出的概率,但在某些情况下仍无法完全避免。
1.线性探测法
线性探测算法:
public class javaDemo {public static void main(String[] args) {//假设地址空间为10,并且初始值为-1int index[] = new int[10];int num;int temp = num % index.length;while (true){
// 如果目标位置不存在数字则存入数据if (index[temp] == -1){index[temp] = num;break;}else {temp = (num+1) % index.length;}}}
}
相关文章:

安全性算法
目录 一、安全性算法 二、基础术语 三、对称加密与非对称加密 四、数字签名 五、 哈希算法 六、哈希算法碰撞与溢出处理 一、安全性算法 安全性算法的必要性: 安全性算法的必要性是因为在现代数字化社会中,我们经常需要传输、存储和处理敏感的数据…...
解决ASP.NET Core的中间件无法读取Response.Body的问题
概要 本文主要介绍如何在ASP.NET Core的中间件中,读取Response.Body的方法,以便于我们实现更多的定制化开发。本文介绍的方法适用于.Net 3.1 和 .Net 6。 代码和实现 现象解释 首先我们尝试在自定义中间件中直接读取Response.Body,代码如…...

DownloadingImages 下载缓存图片,显示图片文字列表
1. 用到的技术点: 1) Codable : 可编/解码 JSON 数据 2) background threads : 后台线程 3) weak self : 弱引用 4) Combine : 取消器/组合操作 5) Publishers and Subscribers : 发布者与订阅者 6) FileManager : 文件管理器 7) NSCache : 缓存 2. 网址: 2.1 测试接口网址: …...

【应用层协议】HTTPS的加密流程
目录 一、认识HTTPS 二、密文 1、对称加密 2、非对称加密 三、HTTPS加密流程 1、建立连接 2、证书验证 3、密钥协商 4、数据传输 5、关闭连接 总结 在数字化时代,互联网已经成为我们生活和工作中不可或缺的一部分。然而,随着数据的不断增加&a…...
最新AI创作系统/AI绘画系统/ChatGPT系统+H5源码+微信公众号版+支持Prompt应用
一、AI创作系统 SparkAi创作系统是基于国外很火的ChatGPT进行开发的AI智能问答系统和AI绘画系统。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图…...

Z410 2023款无人机,专为零基础开发者打造的入门级开源无人机
为什么开发Z410升级款-Easydrone无人机 新手开发者通常在本科阶段加入人工智能行业,对无人机二次开发往往一知半解,面临着C、Python、ROS和mavlink等一系列入门知识,学习起来非常困难,学习的过程中也面临许多挫折。为了帮助零基础…...
elementui修改message消息提示颜色
/* el弹出框样式 */ .el-message {top: 80px !important;border: 0; }.el-message * {color: var(--white) !important;font-weight: 600; }.el-message--success {background: var(--themeBackground); }.el-message--warning {background: var(--gradientBG); }.el-message--…...
Linux和Hadoop的学习
目录 1. Linux的常用快捷键2. Hadoop集群部署问题汇总 1. Linux的常用快捷键 复制:CtrlshiftC 粘贴:CtrlshiftV TAB:补全命令 编写输入:i 退出编写:esc 保存并退出:shift: 2. Hadoop集群部署问…...

通达信指标预警信号,自动发送给微信好友1.0
1.功能介绍:十一节假日期间写了一个,可将股票指标预警信号,自动发送给微信好友/微信群(即电脑端的消息,通过模拟微信操作可在手机上显示)。本工具按通达信写的,如果大智慧,同花顺也能…...
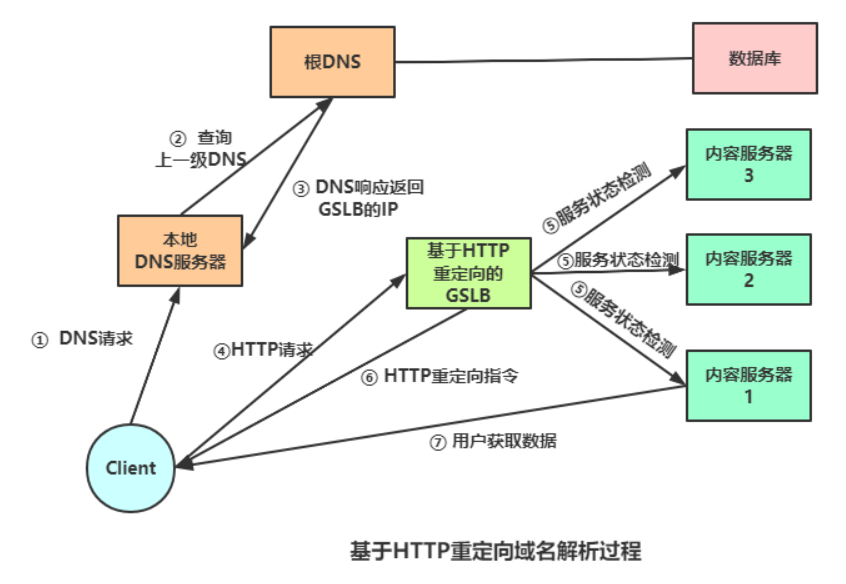
浅谈CDN内容分发与全局负载均衡
CDN简介 CDN的全称是Content Delivery Network,即内容分发网络。CDN是构建在现有网络基础之上的智能虚拟网络,依靠部署在各地的边缘服务器,通过中心平台的负载均衡、内容分发、调度等功能模块,使用户就近获取所需内容,…...
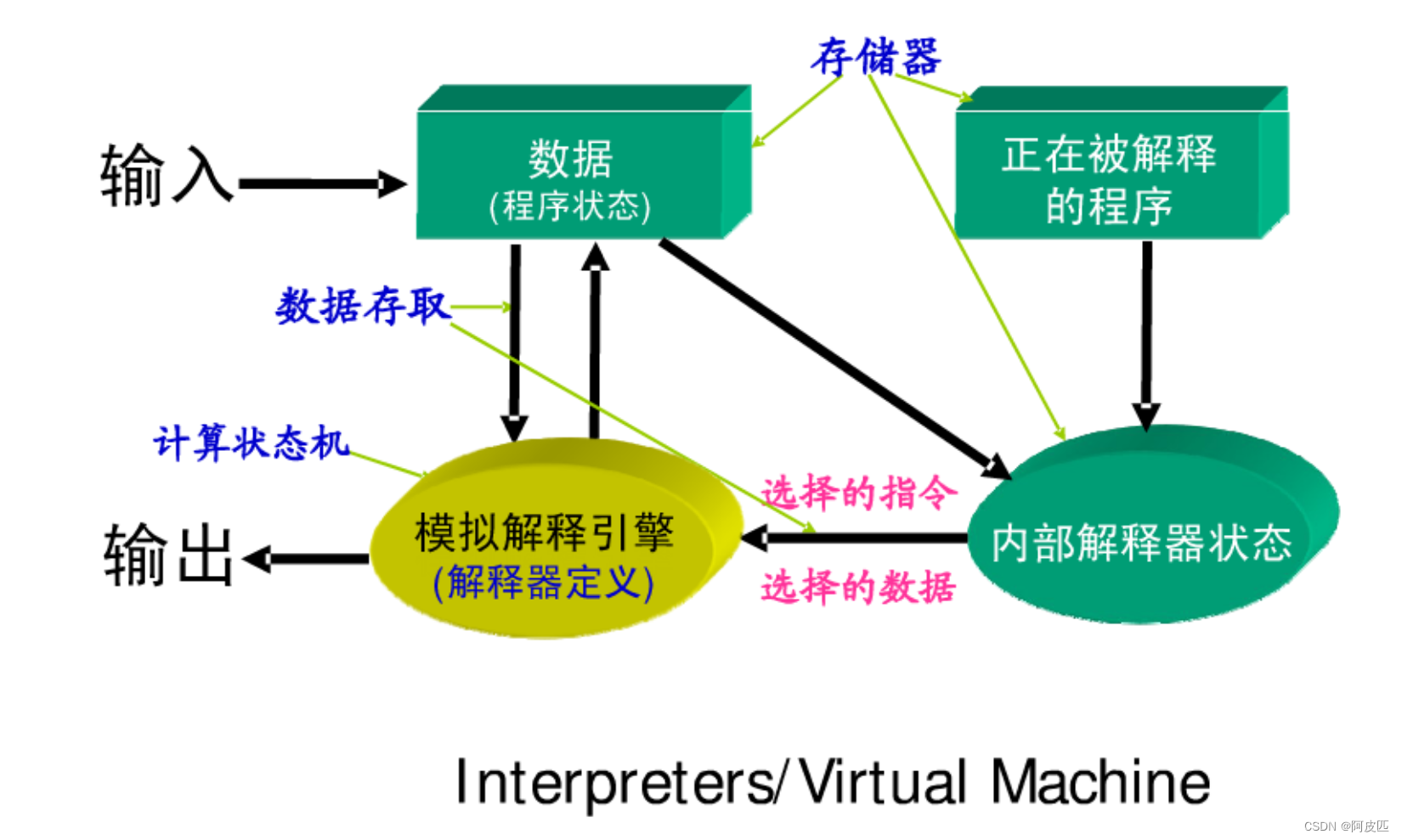
【框架风格】解释器模式
1、描述 解释器框架风格(Interpreter Framework Style)是一种软件架构风格,其核心思想是构建一个解释器(Interpreter)来解释并执行特定领域或问题领域的语言或规则。以下是解释器框架风格的一些特点: 1. 领…...

c++视觉图像线性混合
图像线性混合 使用 cv::addWeighted() 函数对两幅图像进行线性混合。alpha 和 beta 是两幅图像的权重,它们之和应该等于1。gamma 是一个可选的增益,这里设置为0。 你可以通过调整 alpha 的值来改变混合比例。如果 alpha0.5,则两幅图像等权重…...

Doris 2.0.1 DockerFile版 升级实战
1、Doris 2.0.1 DockerFile 的制作 参考 Doris 2.0.1 Dockerfile制作-CSDN博客 2、之前的Doris 集群通过 Docker容器进行的部署,需提前准备好Doris2.0.1的镜像包 参考: 集群升级 - Apache Doris Doris 升级请遵守不要跨两个及以上关键节点版本升级的…...

kotlin aes 加密解密
文章目录 1. key填充2. 加密3. 解密 1. key填充 aes算法对key的字节数有要求 所以对输入的key要做填充处理 fun fillKey(key: String): ByteArray {val random SecureRandom.getInstance("SHA1PRNG")random.setSeed(key.toByteArray())val generator KeyGenerato…...

sqlite3的lib和头文件在哪下载 2023/9/19 上午10:46:43
2023/9/19 上午10:46:43 sqlite3的lib和头文件在哪下载 2023/9/19 上午10:46:54 你可以从SQLite官方网站下载SQLite的lib和头文件。请按照以下步骤进行操作: 打开SQLite官方网站:https://www.sqlite.org/index.html 在页面上方的菜单中选择 “Download”(下载)。 在下载…...

磁通量概述
磁通量指的是设在磁感应强度为B的匀强磁场中,有一个面积为S且与磁场方向垂直的平面,磁感应强度B与面积S的乘积,叫做穿过这个平面的磁通量,简称磁通(Magnetic Flux)。标量,符号“Φ”。在一般情况…...
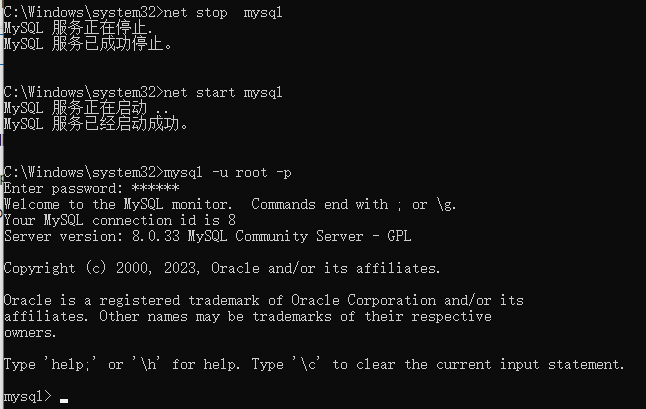
MySql 终端常用指令
一、开发背景 利用数据库实现数据的增删改查 二、开发环境 Window10 mysql-8.0.33-win64 三、实现步骤 1、管理员模式打开终端 2、登录数据库(停止 开启 登录) 具体指令参考 MySql 安装篇 …...

【React-hooks篇幅】自定义hooks
首先得了解自定义 Hooks 跟普通函数区别在于哪里? Hooks 只应该在 React 函数组件内调用,而不应该在普通函数调用。Hooks 能够调用诸如 useState、useEffect、useContext等,普通函数则不能。由此可以通过内置的Hooks等来获得Firber的访问方式…...
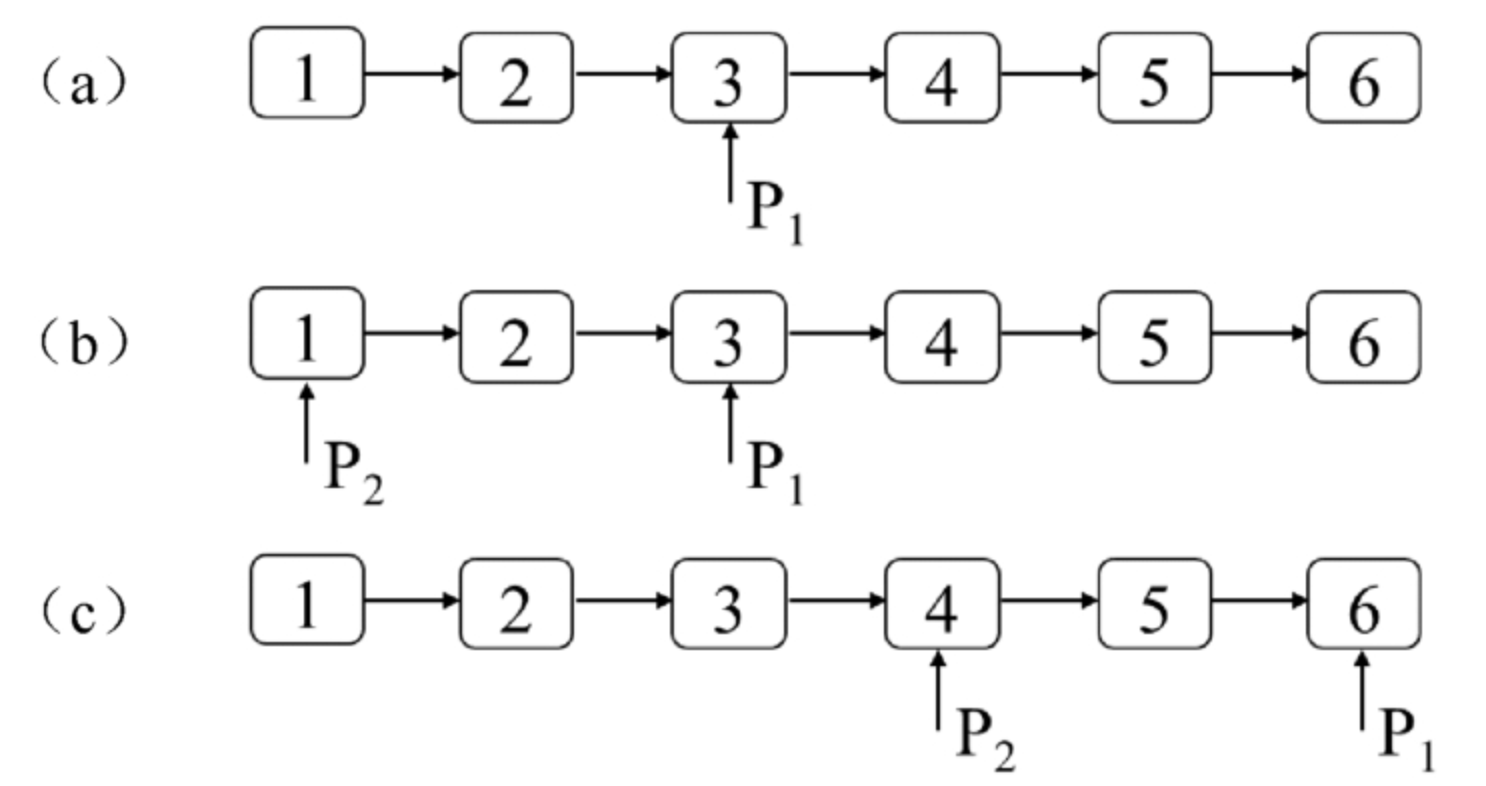
面试算法21:删除倒数第k个节点
题目 如果给定一个链表,请问如何删除链表中的倒数第k个节点?假设链表中节点的总数为n,那么1≤k≤n。要求只能遍历链表一次。 例如,输入图4.1(a)中的链表,删除倒数第2个节点之后的链表如图4.1&a…...
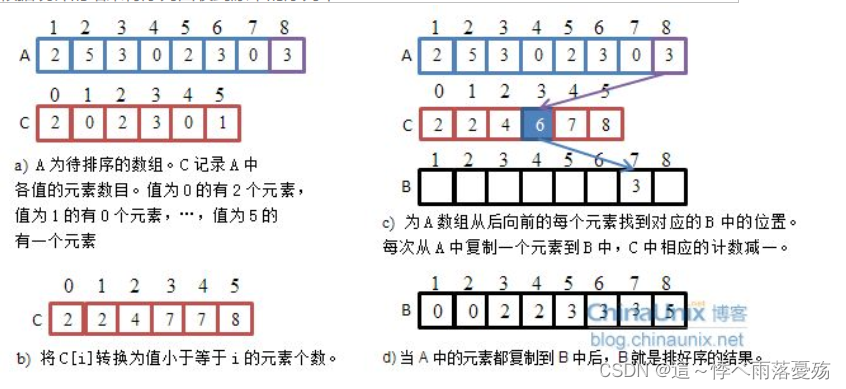
数据结构——排序算法(C语言)
本篇将详细讲一下以下排序算法: 直接插入排序希尔排序选择排序快速排序归并排序计数排序 排序的概念 排序:所谓排序,就是使一串记录,按照其中的某个或某写关键字的大小,按照递增或递减0排列起来的操作。 稳定性的概念…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
