一些常见分布-正态分布、对数正态分布、伽马分布、卡方分布、t分布、F分布等
目录
正态分布
对数正态分布
伽马分布
伽马函数
贝塔函数
伽马分布
卡方分布
F分布
t分布
附录
参考文献
本文主要介绍一些常见的分布,包括正态分布、对数正态分布、伽马分布、卡方分布、F分布、t分布。给出了分布的定义,推导了概率密度函数,以及函数图像。
正态分布

当,称为标准正态分布,即
。
对数正态分布
对数正态分布(logarithmic normal distribution)是指一个随机变量的对数服从正态分布,则该随机变量服从对数正态分布。对数正态分布从短期来看,与正态分布非常接近。但长期来看,对数正态分布向上分布的数值更多一些。

证明:
假设服从的正态分布为
,概率密度函数为
,
服从的分布为
,概率密度函数为
。显然有
。
下面证明的概率密度函数
表达式如上面所示。
一般我们通过分布函数和概率的定义来证明。
,因为
,则
,
即
,两边对
求导,得到:
,即:
,注意到正态分布概率密度函数
如下:

代入后,可得到表达式如上面所示。
伽马分布
伽马函数
在介绍伽马分布之前,我们先对伽马函数有一个基本理解,伽马函数如下:
![]()
是自变量。伽马函数图像如下:
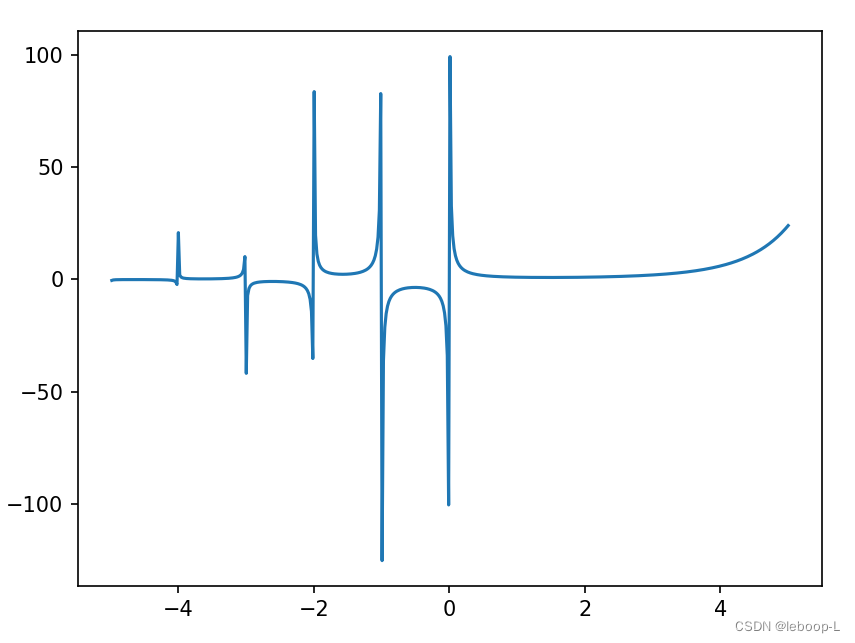
伽马函数图像绘制代码,如下:
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gammaif __name__ == '__main__':x = np.linspace(-5, 5, 500) # -5到5之间生成500个点y = gamma(x) # 计算y的值,也就是伽马函数的值plt.plot(x, y)plt.show() 为了后面方便推导卡方分布,这里我们证明 。
下面利用标准正态分布的概率密度函数曲线下的面积为1来证明。即:
由正态分布对称性,得到
令进行换元,
因为伽马函数如下:
![]()
知道
伽马函数还有其他很多的函数表达式,这里不再累述。
贝塔函数
在概率统计和其他应用学科中会经常用到伽玛函数和贝塔函数,有的反常积分的计算最后也会归结为贝塔函数或伽玛函数。贝塔函数又称为第一类欧拉积分,而第二类欧拉积分就是大名鼎鼎的伽玛函数Γ(x。贝塔函数具有很好的性质,以及实用的递推公式,另外需要注意的是伽玛函数和贝塔函数之间的关系。贝塔函数如下:
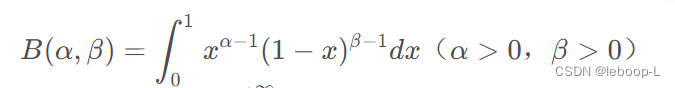
贝塔函数是一个积分形式,为参数。
下面推导伽马函数与贝塔函数之间存在的关系。我们先给出他们的关系:
由伽马函数:
![]()
得到
使用如下积分换元,即
容易得到,并且s=0时,v=1,
时,v=0。变换前后微元关系如下:
则换元后,原式如下:
即:
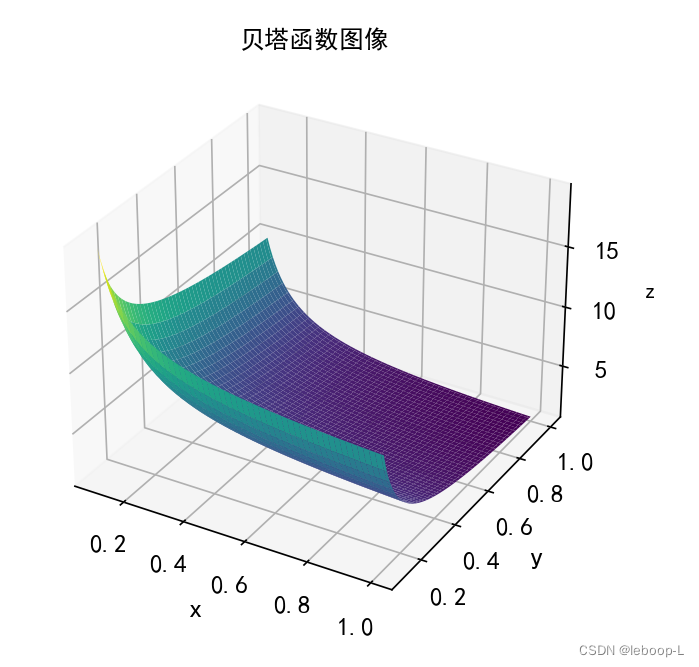
为了直观地理解贝塔函数,下面我们绘制出贝塔函数的三维曲面图像。代码如下:
import numpy as np
from scipy.special import beta
import matplotlib.pyplot as pltif __name__ == '__main__':# 创建一个网格x, y = np.meshgrid(np.linspace(0.1, 1, 100), np.linspace(0.1, 1, 100))print('x=', '\n', x)print('y=', '\n', y)z = beta(x, y)print('z=', '\n', z)plt.rcParams['font.sans-serif'] = ['Simhei'] # 显示中文fig = plt.figure(figsize=(10, 8))ax = fig.add_subplot(111, projection='3d')ax.tick_params(axis="both", labelsize=12)ax.plot_surface(x, y, z, cmap='viridis')ax.set_xlabel('x', fontsize=13)ax.set_ylabel('y', fontsize=13)ax.set_zlabel('z')ax.set_title('贝塔函数图像')plt.show()
运行结果,如下:
伽马分布
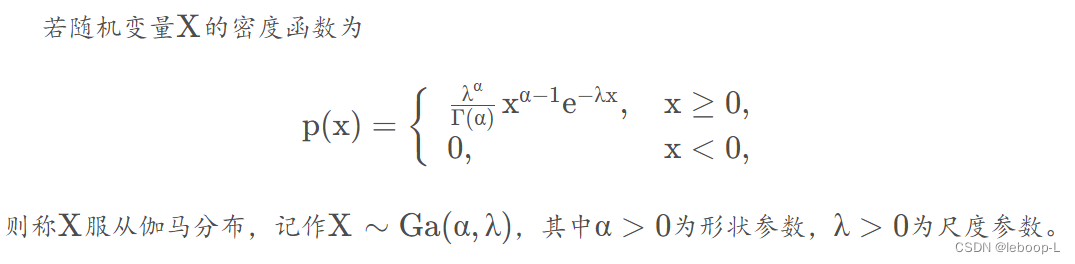
从定义可以看到,伽马分布的概率密度函数的分母中就是伽马函数。 可以通过scipy提供的统计库stats,绘制出正态分布、对数正态分布、伽马分布的概率密度函数曲线,代码如下:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma as gamma_dis
from scipy.stats import lognorm
from scipy.stats import normif __name__ == '__main__':alpha = 2 # 伽马分布的形状参数theta = 2 # 伽马分布的比例参数# 创建一个 sample spacex = np.linspace(0, 10, 200)# 计算概率密度函数 (PDF)gamma_pdf = gamma_dis.pdf(x, alpha, scale=theta) # 伽马分布概率密度函数log_norm_pdf = lognorm.pdf(x, loc=0, s=1) # 对数正态分布概率密度函数norm_pdf = norm.pdf(x, loc=0, scale=1) # 正态分布概率密度函数plt.rcParams['font.sans-serif'] = ['Simhei'] # 显示中文# 绘制伽马分布曲线plt.plot(x, gamma_pdf)plt.plot(x, log_norm_pdf)plt.plot(x, norm_pdf)plt.legend(['伽马分布', '对数正态分布', '正态分布']) # 设置图例plt.title('概率密度函数曲线')plt.xlabel('x')plt.ylabel('概率密度函数值')plt.show()
运行结果如下:
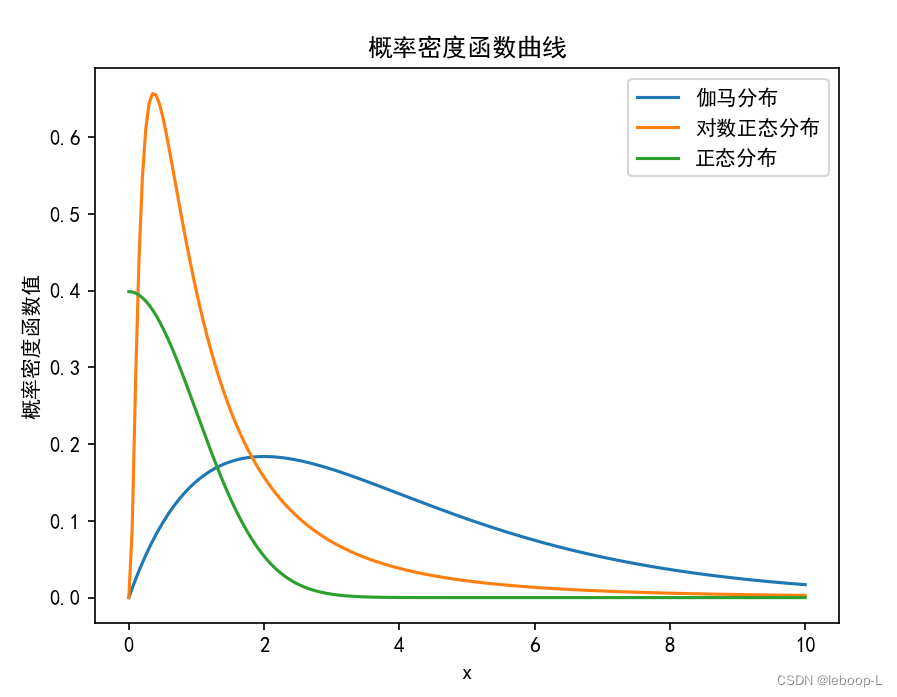
伽马分布有如下重要的性质:
(1)设随机变量,
,且
相互独立,则
。
证明:
假设随机变量的分布为
,概率密度函数为
,随机变量
的概率密度函数分别为
,
。两者的联合概率密度函数为
,因为
相互独立,显然有:
因为
取值都在
,所以
的取值也在
,从而当
时,
。
当时,
,这里将z看成常数,有
使用换元,将x看陈常数,有
,则
,且
,
得到
两边对z求导,得到
。
这就是卷积公式。因为
,
,代入得到
使用换元,当
时,
,并且
,则
根据,得到
,所以
卡方分布
假设n个相互独立的随机变量,均服从标准正态分布(也称独立同分布于标准正态分布)
。则这n个服从标准正态分布的随机变量的平方和
构成一个新的随机变量,其分布规律称为卡方分布(chi-square distribution),记作
,n称为卡方分布的自由度(degree of freedom),记作
。
这个分布由麦克斯韦(James Clerk Maxwell, 1831-1879)在研究空气分子的运动速度的分布时发现的,他发现分子运动速度的平方服从自由度为3的卡方分布,即
。后来又有多人提出这种分布,例如弗里德里希·罗伯特·海尔默特(Friedrich Robert Helmert, 1843-1917)于1875年,故卡方分布有时(在德国常见,因海尔默特是德国人)也称海尔默特分布;另外,这一结果被英国生物统计学家、优生学家、数理统计学创始人和社会达尔文主义理论家卡尔·皮尔逊(Karl Pearson, 1857-1936)推广并于1900年发表。
卡方分布的概率密度函数
下面来推导。
(1)当df=1时,。卡方分布的概率密度函数变为:
假设随机变量的分布函数为
,概率密度函数为
,随机变量
的分布函数为
,概率密度函数为
,随机变量
的分布函数为
,概率密度函数为
。因为
,
服从标准正态分布,有
。
因为
两边对x求导,
因为,所以:
即
事实上,它是的伽马分布,即
。根据如下伽马分布的概率密度函数,很容易得出。
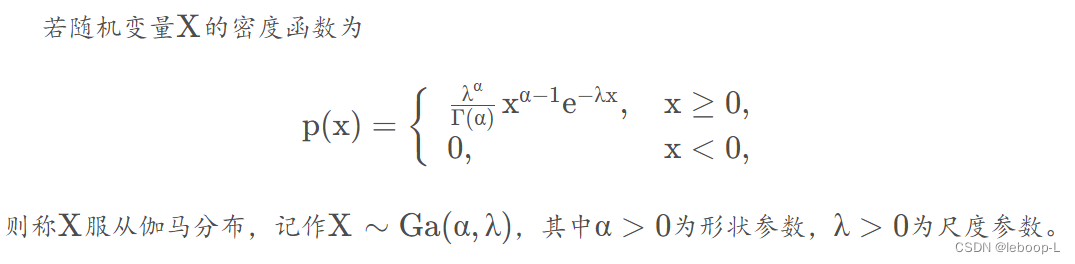
(2)当df=n时,,由上面的结论知道,
。另外因为
相互独立,所以
也相互独立。根据之前证明的如下结论:
如果随机变量,
,且
相互独立,则
。
得到服从
,代入伽马分布,得到如下卡方分布
从结论来看,卡方分布是伽马分布的一个特例,即。也就是说
。
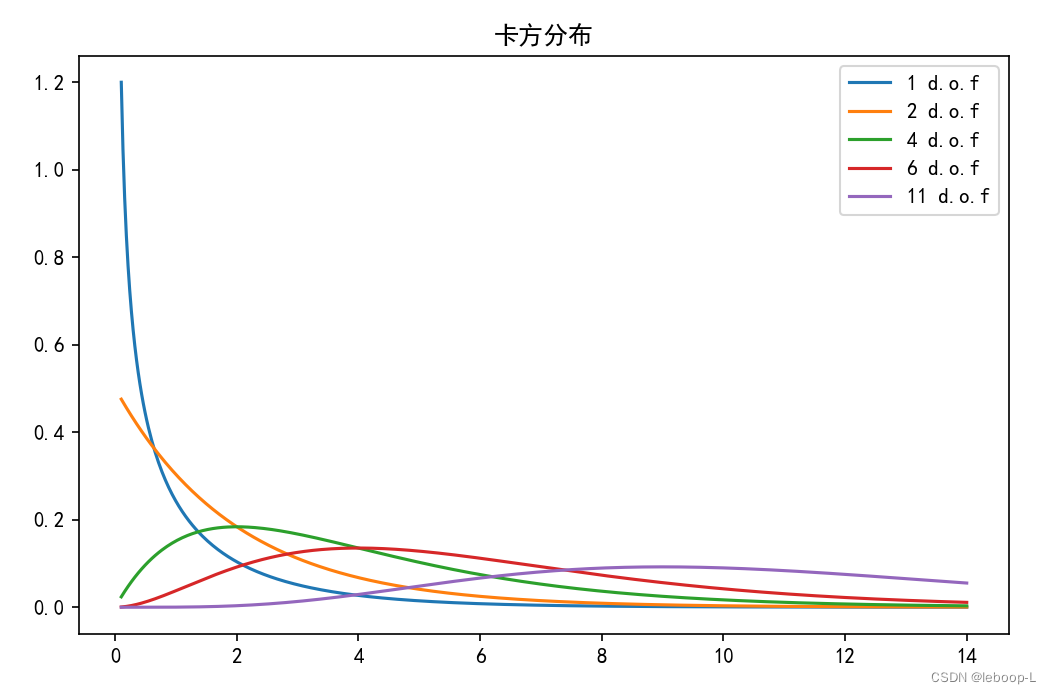
为了直观的观测卡方分布,下面使用python代码绘制卡方分布曲线。代码如下:
import numpy as np
from scipy.special import beta
import matplotlib.pyplot as plt
from scipy import statsif __name__ == '__main__':# # 创建一个网格# x, y = np.meshgrid(np.linspace(0.1, 1, 100), np.linspace(0.1, 1, 100))# print('x=', '\n', x)# print('y=', '\n', y)# z = beta(x, y)# print('z=', '\n', z)#plt.rcParams['font.sans-serif'] = ['Simhei'] # 显示中文# fig = plt.figure(figsize=(10, 8))# ax = fig.add_subplot(111, projection='3d')# ax.tick_params(axis="both", labelsize=12)# ax.plot_surface(x, y, z, cmap='viridis')# ax.set_xlabel('x', fontsize=13)# ax.set_ylabel('y', fontsize=13)# ax.set_zlabel('z')# ax.set_title('贝塔函数图像')# plt.show()X = np.linspace(0.1, 14, 500)plt.subplots(figsize=(8, 5))plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=4), label="4 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=6), label="6 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=11), label="11 d.o.f")plt.title("卡方分布")plt.legend()plt.show()
代码中绘制了自由度为1,2,3,4,11的5个卡方分布,运行结果如下:
F分布
由卡方分布的定义知道,F分布定义可以转换为:如果 ,
,则
为F分布。概率密度函数的证明参见参考文献。
代码如下:
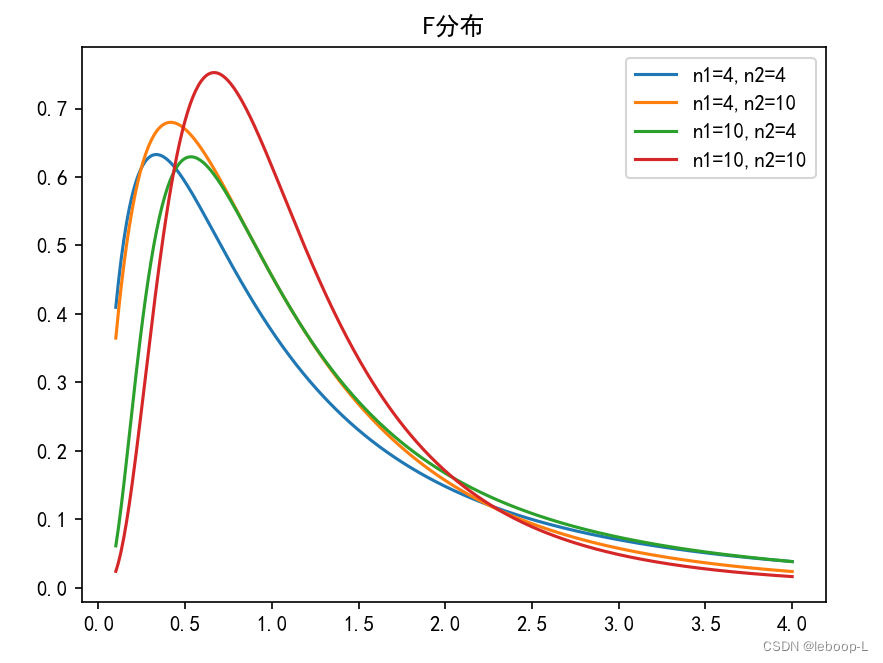
X = np.linspace(0.1, 4, 500)plt.plot(X, stats.f.pdf(X, 4,4), label="n1=4,n2=4")plt.plot(X, stats.f.pdf(X, 4,10), label="n1=4,n2=10")plt.plot(X, stats.f.pdf(X, 10,4), label="n1=10,n2=4")plt.plot(X, stats.f.pdf(X, 10,10), label="n1=10,n2=10")plt.title("F分布")plt.legend()plt.show()运行结果如下:
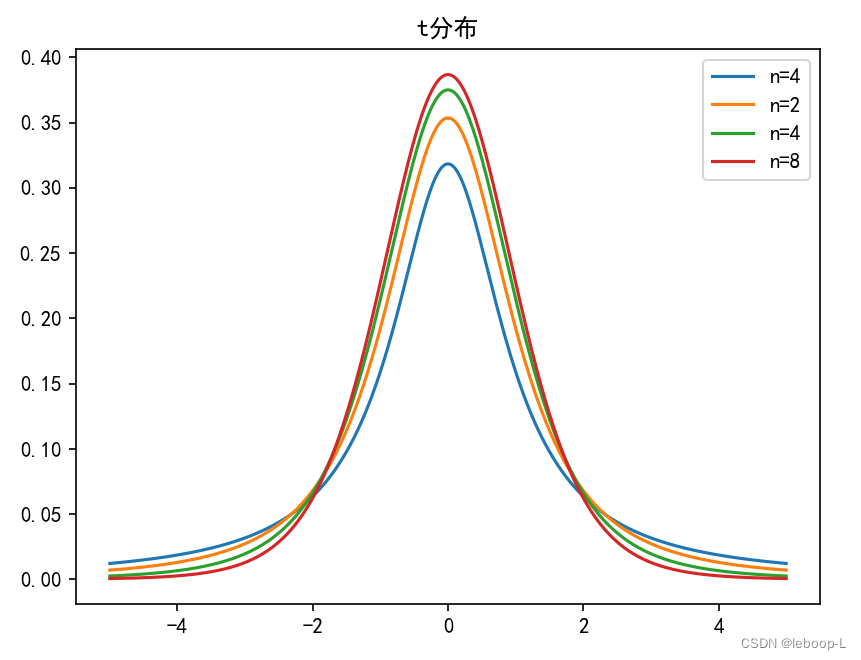
t分布
代码如下:
plt.rcParams["axes.unicode_minus"] = False # 设置显示中文后,负号显示受影响,显示负号X = np.linspace(-5, 5, 1500)plt.plot(X, stats.t.pdf(X, 1), label="n=4")plt.plot(X, stats.t.pdf(X, 2), label="n=2")plt.plot(X, stats.t.pdf(X, 4), label="n=4")plt.plot(X, stats.t.pdf(X, 8), label="n=8")plt.title("t分布")plt.legend()plt.show()运行结果如下:
附录
本节所有代码如下:
import numpy as np
from scipy.special import beta
import matplotlib.pyplot as plt
from scipy import statsif __name__ == '__main__':# 创建一个网格x, y = np.meshgrid(np.linspace(0.1, 1, 100), np.linspace(0.1, 1, 100))print('x=', '\n', x)print('y=', '\n', y)z = beta(x, y)print('z=', '\n', z)plt.rcParams['font.sans-serif'] = ['Simhei'] # 显示中文fig = plt.figure(figsize=(10, 8))ax = fig.add_subplot(111, projection='3d')ax.tick_params(axis="both", labelsize=12)ax.plot_surface(x, y, z, cmap='viridis')ax.set_xlabel('x', fontsize=13)ax.set_ylabel('y', fontsize=13)ax.set_zlabel('z')ax.set_title('贝塔函数图像')plt.show()X = np.linspace(0.1, 14, 500)plt.subplots(figsize=(8, 5))plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=4), label="4 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=6), label="6 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=11), label="11 d.o.f")plt.title("卡方分布")plt.legend()plt.show()X = np.linspace(0.1, 4, 500)plt.plot(X, stats.f.pdf(X, 4,4), label="n1=4,n2=4")plt.plot(X, stats.f.pdf(X, 4,10), label="n1=4,n2=10")plt.plot(X, stats.f.pdf(X, 10,4), label="n1=10,n2=4")plt.plot(X, stats.f.pdf(X, 10,10), label="n1=10,n2=10")plt.title("F分布")plt.legend()plt.show()plt.rcParams["axes.unicode_minus"] = False # 设置显示中文后,负号显示受影响,显示负号X = np.linspace(-5, 5, 1500)plt.plot(X, stats.t.pdf(X, 1), label="n=4")plt.plot(X, stats.t.pdf(X, 2), label="n=2")plt.plot(X, stats.t.pdf(X, 4), label="n=4")plt.plot(X, stats.t.pdf(X, 8), label="n=8")plt.title("t分布")plt.legend()plt.show()
参考文献
高数篇(一)-- Gamma 函数 VS Beta 函数
极坐标与直角坐标二重积分转换
F分布概率密度函数的推导
python绘制正态分布及三大抽样分布的概率密度图像
相关文章:

一些常见分布-正态分布、对数正态分布、伽马分布、卡方分布、t分布、F分布等
目录 正态分布 对数正态分布 伽马分布 伽马函数 贝塔函数 伽马分布 卡方分布 F分布 t分布 附录 参考文献 本文主要介绍一些常见的分布,包括正态分布、对数正态分布、伽马分布、卡方分布、F分布、t分布。给出了分布的定义,推导了概率密度函数&…...

科技云报道:押注向量数据库,为时过早?
科技云报道原创。 在大模型的高调火热之下,向量数据库也获得了前所未有的关注。 近两个月内,向量数据库迎来融资潮,Qdrant、Chroma、Weaviate先后获得融资,Pinecone宣布1亿美元B轮融资,估值达到7.5亿美元。 东北证券…...

铭控传感亮相2023国际物联网展,聚焦“多场景物联感知方案”应用
金秋九月,聚焦IoT基石技术,荟萃最全物联感知企业,齐聚IOTE 2023第20届国际物联网展深圳站。铭控传感携智慧楼宇,数字工厂,智慧消防,智慧泵房等多场景物联感知方案及多品类无线传感器闪亮登场,现…...

前端demo: 实现对图片进行上传前的压缩功能
前端可以使用canvas和File API来对图片进行压缩和缩放处理,以下是一个示例代码 : 压缩方法compressImg这段代码是实现对图片进行上传前的压缩功能 1. 定义了一个压缩图片的函数 compressImg,接受两个参数:file表示要压缩的文件,q…...
)
计算机网络(文章链接汇总)
参考引用 计算机网络微课堂-湖科大教书匠计算机网络(第7版)-谢希仁 计算机网络(一):概述计算机网络(二):物理层计算机网络(三):数据链路层计算机网…...

黑科技-Android
1热更新(热修复):apk不用发版,就能修复bug 原理:我们修复好了bug的时候,把那些有改动的java源码编译成class,再打包成dex,然后通过反射技术放到dexElements数组的最前面,…...
450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。 一般来说,删除节点可分为两个步骤: 首先…...

python安全工具开发基础
文章目录 拷贝、with、is深拷贝、浅拷贝with 三器一闭迭代器生成器闭包装饰器 动态绑定垃圾回收网络编程UdpTcp 协程mysql预处理防止注入 redis未授权/弱密码 拷贝、with 、is a [11, 22, 33] b [11, 22, 33] ca print(id(a)) print(id(b)) print(id(c))print(a b) print(…...

26 docker前后端部署
[参考博客]((257条消息) DockerNginx部署前后端分离项目(SpringBootVue)的详细教程_在docker中安装nginx实现前后端分离_这里是杨杨吖的博客-CSDN博客) (DockerNginx部署前后端分离项目(SpringBootVue)) 安装docker # 1、yum 包更新到最新 yum update # 2、安装需要的软件包…...
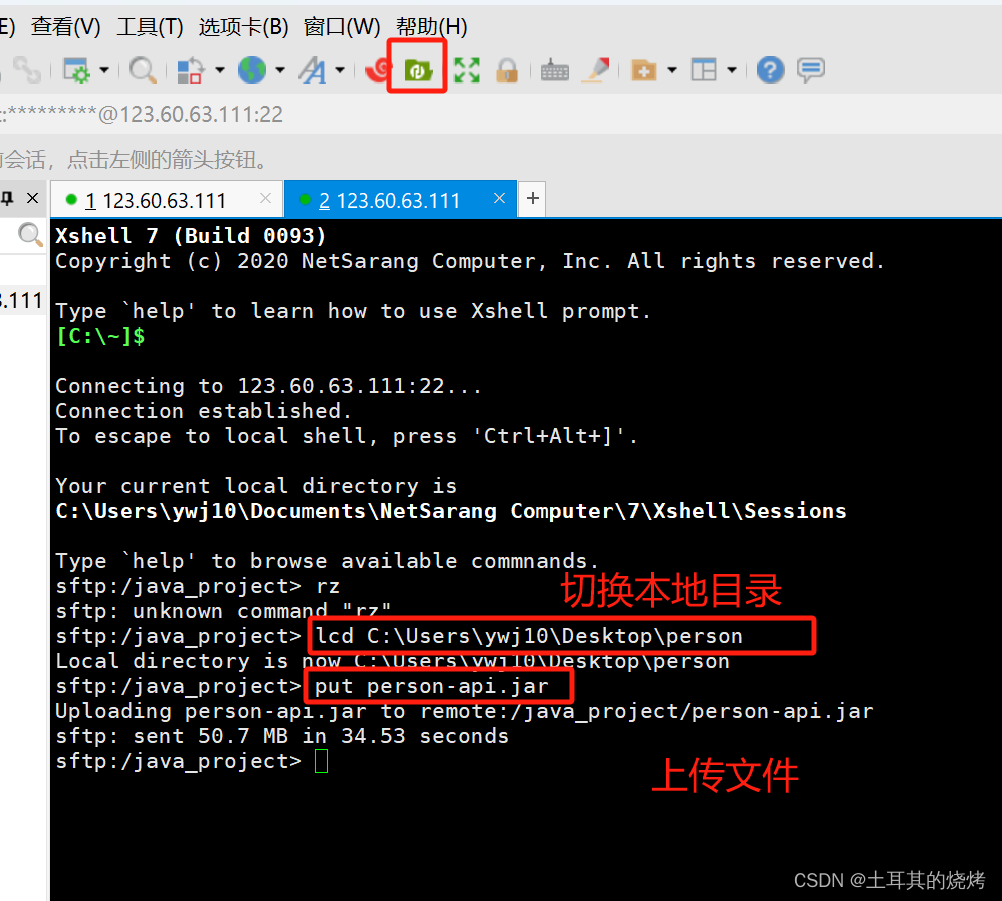
[linux] SFTP文件传输基本命令 --- xshell 直接上传文件
2.sftp - 上传文件:如果上传/下载的是文件夹, 在put/get命令后加上-r参数即可。 上传文件: 把本地服务器的/www/wwwroot目录下面的study.log文件上传到远程服务器的/www/server目录下。 sftp> lcd /www/wwwroot sftp> put study.log /www/server…...

Tomcat 多实例
一、Tomcat 多实例 1、概念: Tomcat 多实例是指在同一台服务器上运行多个独立的 Tomcat 服务器实例。它们可以同时运行在同一台物理服务器或虚拟服务器上,但它们彼此之间是相互独立的,有各自的配置、应用程序和资源。 2、配置:…...

全民拼购模式:电商的新趋势和机遇
全民拼购模式是一种基于社交电商的新型模式,它通过拼团、拼购等方式,让消费者享受更优惠的价格和更便捷的购物体验。这种模式的出现,不仅为电商平台注入了新的活力,也成为了消费者追求高性价比商品的新选择。 全民拼购模式有以下…...

免费使用,媲美Midjourney!微软在Bing Chat等提供—DALL-E 3
微软在官网宣布,将OpenAI最新模型DALL-E 3集成在Bing Chat和Bing Image Create中,并免费提供给用户使用。 据悉,DALL-E 3是一款类Midjourney产品,通过文本就能生成二次元、3D、朋克、涂鸦、素描、黑白、极简、印象派、位面像素等…...

Nacos中AP和CP 切换
CAP理论 这个定理的内容是指的是在一个分布式系统中、Consistency(一致性)、 Availability(可用性)、Partition tolerance(分区容错性),三者不可得兼。 一致性(C):在分布式系统中&a…...
服务器中勒索病毒怎么解决?勒索病毒解密,数据恢复
服务器中勒索病毒是一件低频、高概率的事情。而且一旦用户的服务器中招以后,想要处理无论是经济成本还是时间成本都非常的高。也会对企业的生产经营造成很大的影响。所以绝大多数企业主都很关心服务器中勒索病毒后怎么解决。针对这个问题,云天数据恢复中…...
)
全面解析UDP协议(特点、报文格式、UDP和TCP的区别)
了解UDP(User Datagram Protocol) UDP是无连接通信协议,即在数据传输时,数据的发送端和接收端不建立逻辑连接。简单来说,当一台计算机向另外一台计算机发送数据时,发送端不会确认接收端是否存在࿰…...
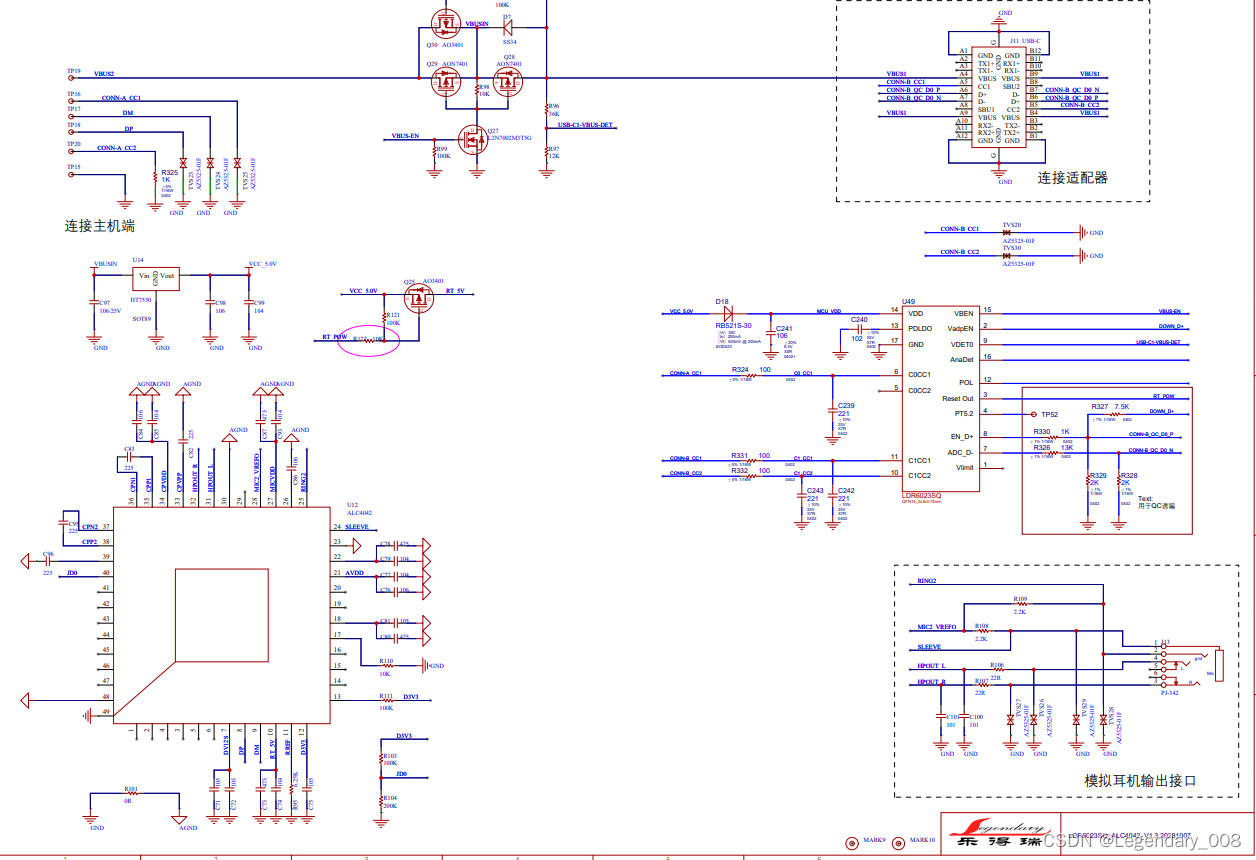
iPhone15手机拓展坞方案,支持手机快充+传输数据功能
手机拓展坞的组合有何意义?首先是数据存储场景,借助拓展坞扩展出的接口,可以连接U盘、移动硬盘等采用USB接口的设备,实现大文件的快速存储或者流转;其次是图片、视频的读取场景,想要读取相机、无人机SD/TF存…...
优化理论笔记
目录 一、前言 二、优化问题的基本要素 三、优化问题分类 四、最优值类型 五、最优化方法分类 六、非约束优化 1、问题定义 2、优化算法 1)一般局部搜索过程 2)集束搜索 3)禁忌搜索 4)模拟退火 5)蛙跳算法…...

FastAPI学习-23.异常处理器 exception_handler
前言 通常我们可以通过 raise 抛出一个 HTTPException 异常,请求参数不合法会抛出RequestValidationError 异常,这是最常见的2种异常。 HTTPException 异常 向客户端返回 HTTP 错误响应,可以使用 raise 触发 HTTPException。 from fastap…...
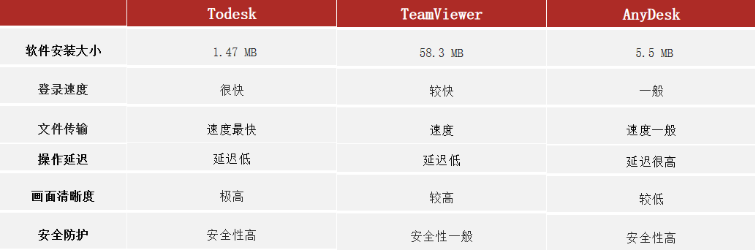
国庆出游远程实测:ToDesk 、TeamViewer、AnyDesk远程控制软件稳定性
ToDesk 、TeamViewer、AnyDesk远程控制软件稳定性 【前言】【实测软件】【测试环境】【实操体验】1. 软件安装2. 登录速度3. 文件传输4. 操作延迟5. 画面清晰度6. 安全防护 【本文小结】 【前言】 随着科技的不断发展,远程控制软件已成为我们生活中不可或缺的一部分…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
