收录一些常见的算法题型
常用算法
字符串
s.trim():去掉字符串首尾的空格s.split("\\s+"):按照空格对字符串分割
树
前中后序遍历
/*** 统一一下* @param root* @return*///前序public static List<Integer> preOrder(TreeNode root){List<Integer> list = new ArrayList();Stack<TreeNode> stack = new Stack();TreeNode cur = root;while(cur!=null || !stack.isEmpty()){//一直往左压入栈while(cur!=null){list.add(cur.val);stack.push(cur);cur = cur.left;}cur = stack.pop();cur = cur.right;}return list;}//中序public List<Integer> inorderTraversal(TreeNode root) {if(root == null){return new ArrayList();}List<Integer> list = new ArrayList();Stack<TreeNode> stack = new Stack();TreeNode cur = root;while(cur != null || !stack.isEmpty()){while(cur!=null){stack.push(cur);cur = cur.left;}cur = stack.pop();list.add(cur.val);cur = cur.right;}return list;}//后序遍历,非递归public static List<Integer> postOrder(TreeNode root){Stack<TreeNode> stack = new Stack<>();List<Integer> list = new ArrayList<>();TreeNode cur = root;TreeNode p = null;//用来记录上一节点while(!stack.isEmpty() || cur != null){while(cur != null){stack.push(cur);cur = cur.left;}cur = stack.peek();
// 后序遍历的过程中在遍历完左子树跟右子树cur都会回到根结点。所以当前不管是从左子树还是右子树回到根结点都不应该再操作了,应该退回上层。
// 如果是从右边再返回根结点,应该回到上层。//主要就是判断出来的是不是右子树,是的话就可以把根节点=加入到list了if(cur.right == null || cur.right == p){list.add(cur.val);stack.pop();p = cur;cur = null;}else{cur = cur.right;}}return list;
}
回溯
- 寻找所有的组合,给的candidates中没有重复的元素,candidates中的元素可以重复取
题目链接:https://leetcode.cn/problems/combination-sum/submissions/
class Solution {private List<List<Integer>> ans;// 普通的回溯+关键的去重使用startIndexpublic List<List<Integer>> combinationSum(int[] candidates, int target) {ans = new ArrayList<>();backtracking(0,candidates,target,0,new ArrayList<>());return ans;}public void backtracking(int startIndex,int[] candidates,int target,int sum,List<Integer> path){if(sum==target){ans.add(new ArrayList<>(path));}if(sum>target){return;}for(int i=startIndex;i<candidates.length;i++){path.add(candidates[i]);backtracking(i,candidates,target,sum+candidates[i],path);path.remove(path.size()-1);}}
}
- 组合问题:candidtes无序,candidates中元素有重复的,要求计算组合数,且candidates中同一个数只能取一次
class Solution {private List<List<Integer>> ans;public List<List<Integer>> combinationSum2(int[] candidates, int target) {ans = new ArrayList<>();Arrays.sort(candidates);backtracking(0,candidates,target,0,new ArrayList<>());return ans;}public void backtracking(int startIndex,int[] candidates,int target,int sum,List<Integer> path){if(sum==target){ans.add(new ArrayList<>(path));}if(sum>target){return;}for(int i=startIndex;i<candidates.length;i++){// 这里是i>startIndex表示每次遍历时,如果跟上一次相同就不用再次遍历if(i>startIndex&&candidates[i-1]==candidates[i]){continue;}path.add(candidates[i]);backtracking(i+1,candidates,target,sum+candidates[i],path);path.remove(path.size()-1);}}
}
二分
- 注意要是升序或者降序,时间复杂度:O(log n)
- 正常的二分写法
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2if (nums[middle] > target) {right = middle - 1; // target 在左区间,所以[left, middle - 1]} else if (nums[middle] < target) {left = middle + 1; // target 在右区间,所以[middle + 1, right]} else { // nums[middle] == targetreturn middle; // 数组中找到目标值,直接返回下标}}// 未找到目标值return -1;}
};
- 变形写法,寻找端点,题目链接:https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/description/
class Solution {public int[] searchRange(int[] nums, int target) {// 因为要取得O(log n)的时间复杂度,因此考虑使用二分法return new int[] {findleft(nums,target),findright(nums,target)};}// 寻找小于等于target的最大的数的下标public int findleft(int[] nums,int target){int l=0,r=nums.length-1;while(l<=r){int mid = (l+r)/2;if(nums[mid]>=target){r = mid-1;}else{l = mid+1;}}if(l>=nums.length||nums[l]!=target){return -1;}return l;}// 寻找大于等于target的最大的数的下标public int findright(int[] nums,int target){int l=0,r=nums.length-1;while(l<=r){int mid = (l+r)/2;if(nums[mid]<=target){l = mid+1;}else{r = mid-1;}}if(r<0||nums[r]!=target){return -1;}return r;}
}
- 变形写法,部分有序:https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array/
排序算法
选择排序
思路:每一轮选取未排定的部分中最小的部分交换到未排定部分的最开头,经过若干个步骤,就能排定整个数组。即:先选出最小的,再选出第 2 小的,以此类推。
import java.util.Arrays;public class Solution {// 选择排序:每一轮选择最小元素交换到未排定部分的开头public int[] sortArray(int[] nums) {int len = nums.length;// 循环不变量:[0, i) 有序,且该区间里所有元素就是最终排定的样子for (int i = 0; i < len - 1; i++) {// 选择区间 [i, len - 1] 里最小的元素的索引,交换到下标 iint minIndex = i;for (int j = i + 1; j < len; j++) {if (nums[j] < nums[minIndex]) {minIndex = j;}}swap(nums, i, minIndex);}return nums;}private void swap(int[] nums, int index1, int index2) {int temp = nums[index1];nums[index1] = nums[index2];nums[index2] = temp;}public static void main(String[] args) {int[] nums = {5, 2, 3, 1};Solution solution = new Solution();int[] res = solution.sortArray(nums);System.out.println(Arrays.toString(res));}
}
总结:
-
算法思想 1:贪心算法:每一次决策只看当前,当前最优,则全局最优。注意:这种思想不是任何时候都适用。
-
算法思想 2:减治思想:外层循环每一次都能排定一个元素,问题的规模逐渐减少,直到全部解决,即「大而化小,小而化了」。运用「减治思想」很典型的算法就是大名鼎鼎的「二分查找」。
-
优点:交换次数最少。
- 时间复杂度:O(N^2),这里 N 是数组的长度;
- 空间复杂度:O(1),使用到常数个临时变量。
插入排序
思路:每次将一个数字插入一个有序的数组里,成为一个长度更长的有序数组,有限次操作以后,数组整体有序。
public class Solution {// 插入排序:稳定排序,在接近有序的情况下,表现优异public int[] sortArray(int[] nums) {int len = nums.length;// 循环不变量:将 nums[i] 插入到区间 [0, i) 使之成为有序数组for (int i = 1; i < len; i++) {// 先暂存这个元素,然后之前元素逐个后移,留出空位int temp = nums[i];int j = i;// 注意边界 j > 0while (j > 0 && nums[j - 1] > temp) {nums[j] = nums[j - 1];j--;}nums[j] = temp;}return nums;}
}
-
优化:「将一个数字插入一个有序的数组」这一步,可以不使用逐步交换,使用先赋值给「临时变量」,然后「适当的元素」后移,空出一个位置,最后把「临时变量」赋值给这个空位的策略(就是上面那张图的意思)。编码的时候如果不小心,可能会把数组的值修改,建议多调试;
-
特点:「插入排序」可以提前终止内层循环(体现在 nums[j - 1] > temp 不满足时),在数组「几乎有序」的前提下,「插入排序」的时间复杂度可以达到 O(N)O(N)O(N);
-
由于「插入排序」在「几乎有序」的数组上表现良好,特别地,在「短数组」上的表现也很好。因为「短数组」的特点是:每个元素离它最终排定的位置都不会太远。为此,在小区间内执行排序任务的时候,可以转向使用「插入排序」。
复杂度分析:
- 时间复杂度:O(N^2),这里 N 是数组的长度;
- 空间复杂度:O(1),使用到常数个临时变量。
归并排序
思路:借助额外空间,合并两个有序数组,得到更长的有序数组。
class Solution {//归并排序public int[] sortArray(int[] nums) {return mergeSort(nums, 0, nums.length-1); }public int[] mergeSort(int[] nums, int left, int right){//递归退出条件//如果左指针大于右指针,就退出循环//经过左右拆分,数组元素形成单个元素的树if(left >=right){return nums;}//数组中的中位数int mid = (right+left)/2;//数组左拆分mergeSort(nums, left, mid);//数组右拆分mergeSort(nums, mid+1, right);//数组合并,将单个元素进行合并return merge(nums, left, mid, right);}public int[] merge(int[] nums, int left, int mid, int right){//定义一个临时数组,存储排序好的元素int[] temp = new int[right-left+1];//左排序的元素数组的左指针int i = left;//右排序的元素数组的左指针int j = mid+1;//定义一个指向临时数组的左指针int t = 0;//循环判断条件//左数组到mid,右数组到right//左右数组都有元素的时候,进行比较while(i<=mid&&j<=right){//取左右数组中较小的元素,填入临时数组中//并将较小元素所在数组的左指针和临时数组的左指针都一起右移if(nums[i]<=nums[j]){temp[t++] = nums[i++];}else{temp[t++] = nums[j++];}}//当左右数组其中一个数组没有元素的时候//如果左数组中还有剩余元素,就将剩余元素全部加入到临时数组中while(i<=mid){temp[t++]=nums[i++];}//如果有数组中还有元素,就将剩余元素全部加入到临时数组中while(j<=right){temp[t++] = nums[j++];}//将临时数组的元素复制到原数组中去for(int k = 0; k<temp.length;k++){//特别注意这便nums数组起始位置要从 k+left开始 //原因在加右数组的时候,起始位置要加left//这里不理解,直接把它记住。nums[left+k]=temp[k];}//返回原数组return nums;}
}
「归并排序」比「快速排序」好的一点是,它借助了额外空间,可以实现「稳定排序」,Java 里对于「对象数组」的排序任务,就是使用归并排序(的升级版 TimSort,在这里就不多做介绍)。
复杂度分析:
-
时间复杂度:O(NlogN),这里 N 是数组的长度;
-
空间复杂度:O(N),辅助数组与输入数组规模相当。
快速排序
基本思路:快速排序每一次都排定一个元素(这个元素呆在了它最终应该呆的位置),然后递归地去排它左边的部分和右边的部分,依次进行下去,直到数组有序;
import java.util.Random;public class Solution {// 快速排序 1:基本快速排序/*** 列表大小等于或小于该大小,将优先于 quickSort 使用插入排序*/private static final int INSERTION_SORT_THRESHOLD = 7;private static final Random RANDOM = new Random();public int[] sortArray(int[] nums) {int len = nums.length;quickSort(nums, 0, len - 1);return nums;}private void quickSort(int[] nums, int left, int right) {// 小区间使用插入排序if (right - left <= INSERTION_SORT_THRESHOLD) {insertionSort(nums, left, right);return;}int pIndex = partition(nums, left, right);quickSort(nums, left, pIndex - 1);quickSort(nums, pIndex + 1, right);}/*** 对数组 nums 的子区间 [left, right] 使用插入排序** @param nums 给定数组* @param left 左边界,能取到* @param right 右边界,能取到*/private void insertionSort(int[] nums, int left, int right) {for (int i = left + 1; i <= right; i++) {int temp = nums[i];int j = i;while (j > left && nums[j - 1] > temp) {nums[j] = nums[j - 1];j--;}nums[j] = temp;}}// 用来确定pivot的位置private int partition(int[] nums, int left, int right) {int randomIndex = RANDOM.nextInt(right - left + 1) + left;// 交换到最左边swap(nums, left, randomIndex);// 基准值int pivot = nums[left];int lt = left;// 循环不变量:// all in [left + 1, lt] < pivot// all in [lt + 1, i) >= pivotfor (int i = left + 1; i <= right; i++) {if (nums[i] < pivot) {lt++;swap(nums, i, lt);}}swap(nums, left, lt);return lt;}private void swap(int[] nums, int index1, int index2) {int temp = nums[index1];nums[index1] = nums[index2];nums[index2] = temp;}
}
复杂度分析:
- 时间复杂度:O(NlogN),这里 N 是数组的长度;
- 空间复杂度:O(logN),这里占用的空间主要来自递归函数的栈空间。
冒泡排序
基本思想:
- 从序列的第一个元素开始,对相邻的两个元素进行比较,如果它们的顺序错误就交换它们的位置,即将较大的元素往后移动,直到遍历到序列的最后一个元素。
- 对剩下的元素重复上述步骤,直到整个序列都已经有序。
public class Solution {public int[] sortArray(int[] nums) {int len = nums.length;for (int i = len - 1; i >= 0; i--) {// 先默认数组是有序的,只要发生一次交换,就必须进行下一轮比较,// 如果在内层循环中,都没有执行一次交换操作,说明此时数组已经是升序数组boolean sorted = true;for (int j = 0; j < i; j++) {if (nums[j] > nums[j + 1]) {swap(nums, j, j + 1);sorted = false;}}if (sorted) {break;}}return nums;}private void swap(int[] nums, int index1, int index2) {int temp = nums[index1];nums[index1] = nums[index2];nums[index2] = temp;}
}
复杂度分析:
- 时间复杂度:O(N^2),这里 N 是数组的长度;
- 空间复杂度:O(1),使用到常数个临时变量。
并查集
可以按照多叉树的思想来考虑,我们使用数组的方式来构造一颗两层的多叉树,一般可以套用如下模板:
public static void init(){for(int i=0;i<father.length;i++){father[i] = i;}}// 连接两条边public static void union(int a,int b){father[find(a)]=find(b);}// 寻找a的根public static int find(int a){return a==father[a]?a:(father[a]=find(father[a]));}
可以参考华为机试题:https://mp.weixin.qq.com/s/BlpsEoitip7ugQYgezCd3g
相关文章:

收录一些常见的算法题型
常用算法 字符串 s.trim():去掉字符串首尾的空格s.split("\\s"):按照空格对字符串分割 树 前中后序遍历 /*** 统一一下* param root* return*///前序public static List<Integer> preOrder(TreeNode root){List<Integer> list new ArrayList();Stac…...
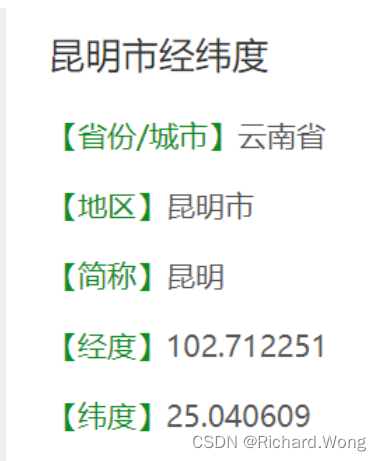
Node-RED系列教程-25node-red获取天气
安装节点:node-red-contrib-weather 节点图标如下: 使用说明:node-red-contrib-weather (node) - Node-RED 流程图中填写经度和纬度即可。 演示: json内容: {...

Rust中的枚举和模式匹配
专栏简介:本专栏作为Rust语言的入门级的文章,目的是为了分享关于Rust语言的编程技巧和知识。对于Rust语言,虽然历史没有C、和python历史悠远,但是它的优点可以说是非常的多,既继承了C运行速度,还拥有了Java…...

好物周刊#19:开源指北
https://github.com/cunyu1943/JavaPark https://yuque.com/cunyu1943 村雨遥的好物周刊,记录每周看到的有价值的信息,主要针对计算机领域,每周五发布。 一、项目 1. Vditor 一款浏览器端的 Markdown 编辑器,支持所见即所得、…...
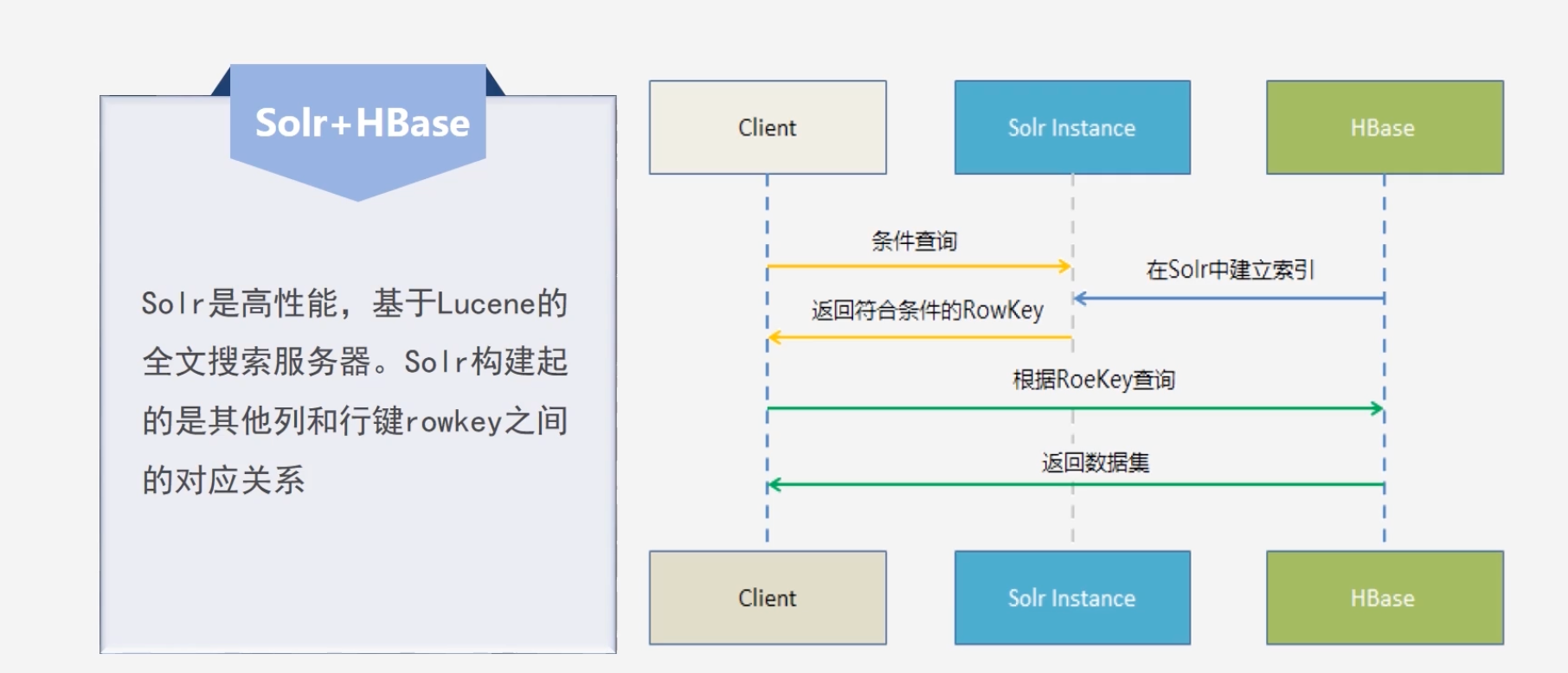
分布式数据库(林子雨慕课课程)
文章目录 4. 分布式数据库HBase4.1 HBase简介4.2 HBase数据模型4.3 HBase的实现原理4.4 HBase运行机制4.5 HBase的应用方案4.6 HBase安装和编程实战 4. 分布式数据库HBase 4.1 HBase简介 HBase是BigTable的开源实现 对于网页搜索主要分为两个阶段 1.建立整个网页索引…...

使用UiPath和AA构建的解决方案 3. CRM 自动化
您是否曾经从一个应用程序中查找数据并更新另一个系统? 在许多情况下,人们在系统之间复制和移动数据。有时,可能会发生“转椅活动”,从而导致人为失误。RPA可以帮助我们自动化这些活动,使其更快,同时还可以消除任何人为错误。 在这个项目中,我们将在客户服务中自动化一…...
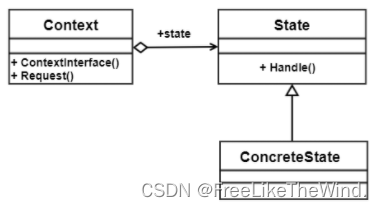
【C++设计模式之状态模式:行为型】分析及示例
简介 状态模式(State Pattern)是一种行为型设计模式,它允许对象在内部状态改变时改变其行为,看起来就像是改变了其类。状态模式将对象的状态封装成不同的类,并使得对象在不同状态下有不同的行为。 描述 状态模式通过…...
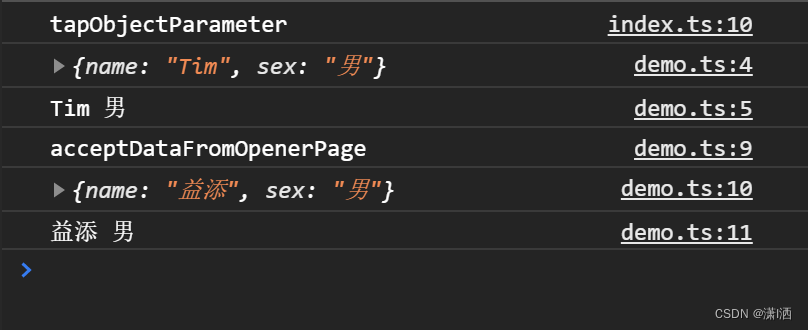
微信小程序使用路由传参和传对象的方法
近期在做微信小程序开发,在页面跳转时,需要携带参数到下一个页面,尤其是将对象传入页面。为了方便重温,特此记录。 路由传字符串参数 原始页面 传递字符串参数比较简单。路由跳转有两种方式,一种是通过navigator组件…...
)
中国创可贴市场研究与未来预测报告(2023版)
内容简介: 创可贴由胶布(带)、吸水垫、防粘层等组成,胶布以弹性布、棉布、无纺布或PE、PVC、PU打孔膜、TPU等材料为常见基材,涂以氧化锌和橡胶为主要原料的胶浆或医用压敏胶黏剂或丙烯酸酯胶粘剂制成。 目前中国主要…...

水库安全监测方案(实时数据采集、高速数据传输)
一、引言 水库的安全监测对于防止水灾和保障人民生命财产安全至关重要。为了提高水库安全监测的效率和准确性,本文将介绍一种使用星创易联DTU200和SG800 5g工业路由器部署的水库安全监测方案。 二、方案概述 本方案主要通过使用星创易联DTU200和SG800 5g工业路…...

vue项目 ueditor使用示例
简介 UEditor是由百度Web前端研发部开发的所见即所得富文本web编辑器,具有轻量,功能丰富,易扩展等特点。UEditor支持常见的文本编辑功能,如字体、颜色、大小、加粗、斜体、下划线、删除线等,同时还支持超链接、图片上…...

深度学习笔记之优化算法(四)Nesterov动量方法的简单认识
机器学习笔记之优化算法——Nesterov动量方法的简单认识 引言回顾:梯度下降法与动量法Nesterov动量法Nesterov动量法的算法过程描述总结 引言 上一节对动量法进行了简单认识,本节将介绍 Nesterov \text{Nesterov} Nesterov动量方法。 回顾:…...

比 N 小的最大质数
系列文章目录 进阶的卡莎C++_睡觉觉觉得的博客-CSDN博客数1的个数_睡觉觉觉得的博客-CSDN博客双精度浮点数的输入输出_睡觉觉觉得的博客-CSDN博客足球联赛积分_睡觉觉觉得的博客-CSDN博客大减价(一级)_睡觉觉觉得的博客-CSDN博客小写字母的判断_睡觉觉觉得的博客-CSDN博客纸币(…...

JavaScript 生成随机颜色
代码 function color(color) {return (color "0123456789abcdef"[Math.floor(Math.random() * 6)]) && (color.length 6 ? color : arguments.callee(color)); }使用 // 用法1:全部随机生成 "#" color(""); // #201050…...

Savepoints
语法 SAVEPOINT 名称 RELEASE SAVEPOINT 名称 ROLLBACK TRANSACTION TO SAVEPOINT 名称 Savepoints 与BEGIN和COMMIT类似的创建事务的方法,名称不要求唯一且可以嵌套使用。 可以用在BEGIN…COMMIT定义的事务内部或外部。当在外部时,最外层的savepoin…...

【MySQL】基本查询(二)
文章目录 一. 结果排序二. 筛选分页结果三. Update四. Delete五. 截断表六. 插入查询结果结束语 操作如下表 //创建表结构 mysql> create table exam_result(-> id int unsigned primary key auto_increment,-> name varchar(20) not null comment 同学姓名,-> chi…...
Qt:多语言支持,构建全面应用程序“
Qt:强大API、简化框架、多语言支持,构建全面应用程序" 强大的API:Qt提供了丰富的API,包括250多个C类,基于模板的集合、序列化、文件操作、IO设备、目录管理、日期/时间等功能。还包括正则表达式处理和支持2D/3D…...
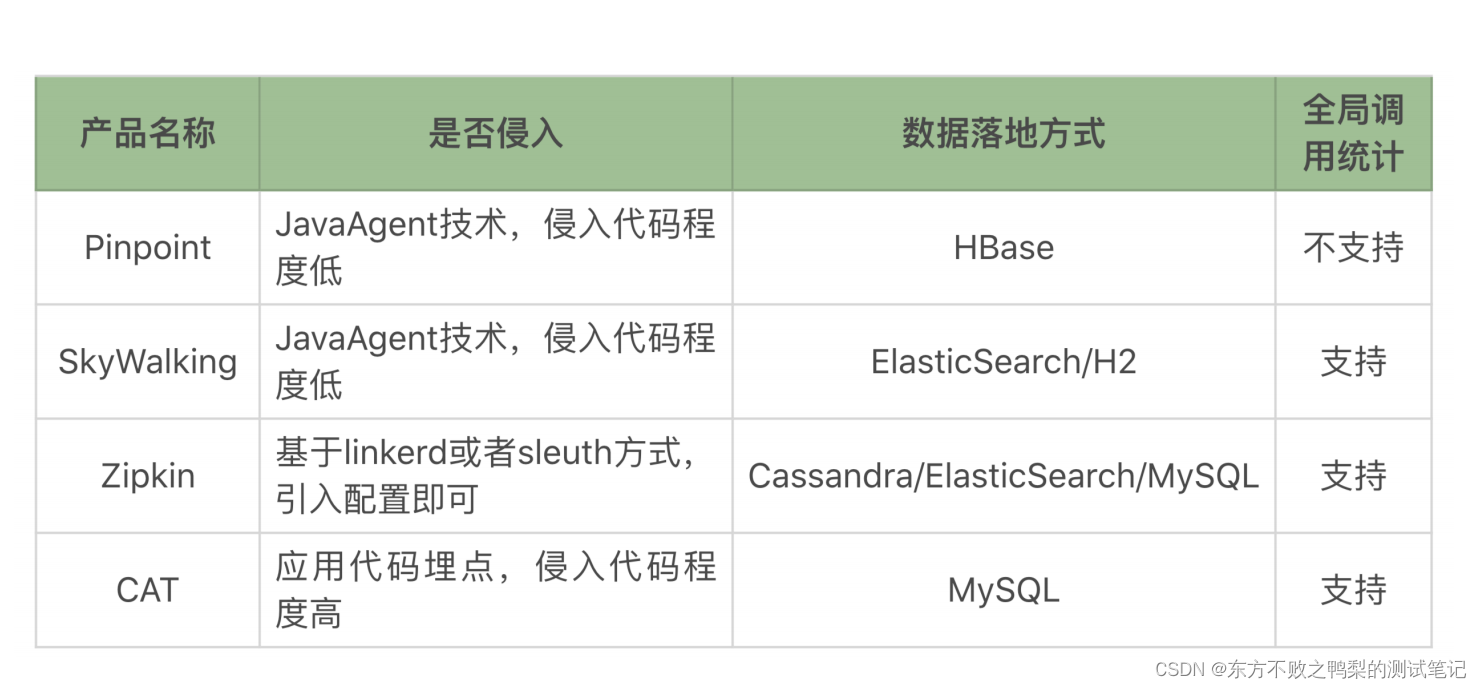
性能监控-链路级监控工具
常见的链路监控工具,我们都称之为 APM 开源工具 几个开源的好用的工具,它们分别是 Pinpoint、SkyWalking、Zipkin、CAT 网络上也有人对这几个工具做过测试 比对,得到的结论是每个产品对性能的影响都在 10% 以下,其中 SkyWalking …...

clickonce 程序发布到ftp在使用cnd 加速https 支持下载,会不会报错
ClickOnce 是一种用于发布和部署.NET应用程序的技术,通常用于本地部署或通过网络分发应用程序。将 ClickOnce 程序发布到 FTP 服务器并使用 CDN(内容分发网络)进行加速是可能的,但要确保配置正确以避免出现错误。 在使用 CDN 加速…...
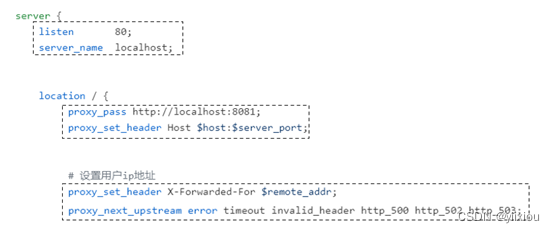
Nginx详细学习记录
1. Nginx概述 Nginx是一个轻量级的高性能HTTP反向代理服务器,同时它也是一个通用类型的代理服务器,支持绝大部分协议,如TCP、UDP、SMTP、HTTPS等。 1.1 Nginx基础架构 Nginx默认采用多进程工作方式,Nginx启动后,会运行…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
