最短路径专题8 交通枢纽 (Floyd求最短路 )
题目: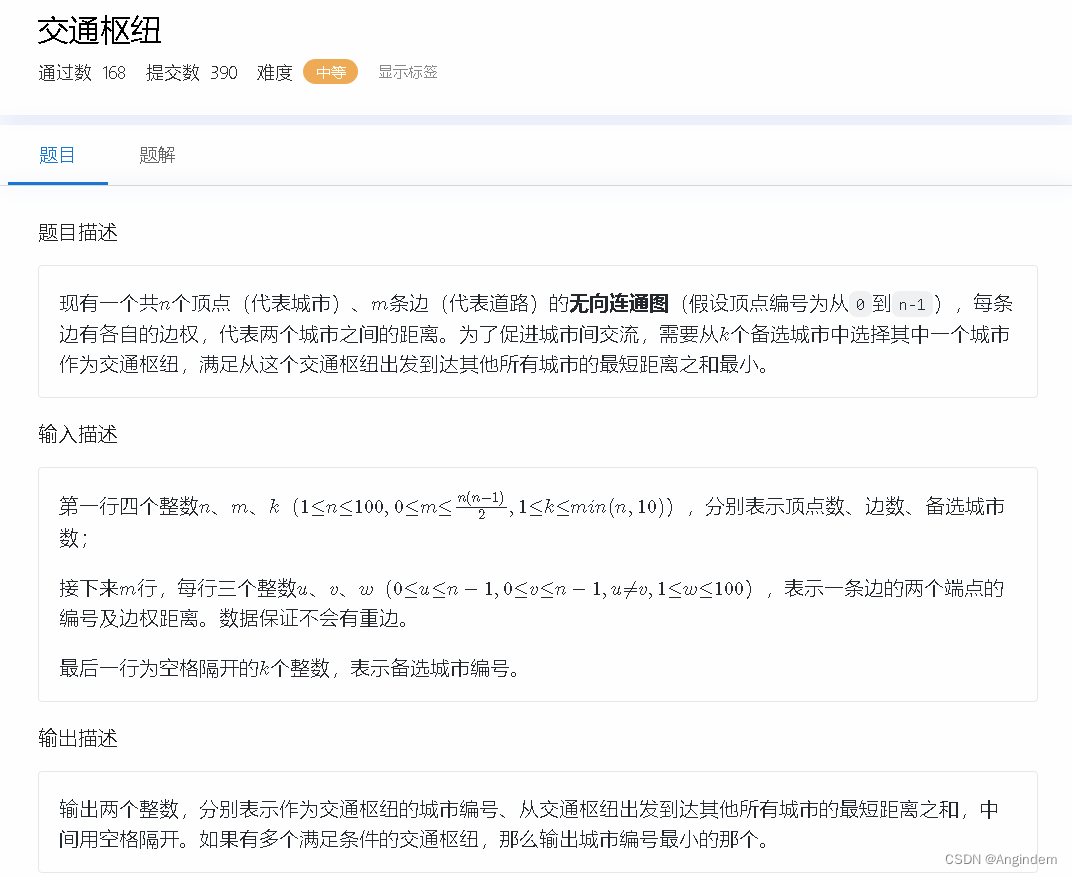
样例:
|
| 0 7 |
思路:
由题意,绘制了该城市的地图之后,由给出的 k 个编号作为起点,求该点到各个点之间的最短距离之和最小的点是哪个,并输出该点,和该点到各个点之间的最短距离之和。
这又是一个多起点多终点的题型,所以用 Floyd 算法非常的有效率。
代码详解如下:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>
#define endl '\n'
#define x first
#define y second
#define mk make_pair
#define int long long
#define NO puts("NO")
#define YES puts("YES")
#define umap unordered_map
#define INF 0x3f3f3f3f
#define All(x) (x).begin(),(x).end()
#pragma GCC optimize(3,"Ofast","inline")
#define ___G std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10,M = 500;
using PII = pair<int,int>;int n,m,k;int dist[M][M]; // 定义各个点之间的最短距离数组// 初始化各个点之间的最短距离
inline void Init()
{memset(dist,INF,sizeof dist);// 自身点之间的距离是 0for(int i = 0;i <= n;++i){dist[i][i] = 0;}
}inline void Floyd()
{// 这一层是中间点for(int k = 0;k < n;++k){// 这一层是 i 点for(int i = 0;i < n;++i){// 这一层是 j 点for(int j = 0;j < n;++j){// 更新选取最短的 i 到 j 的最短距离方案 ,即 i 到 k ,k 再到 jdist[i][j] = min(dist[i][j],dist[i][k] + dist[k][j]);}}}
}// 由 x 点到各个点之间的最短距离之和
inline int DistSum(int x)
{int sum = 0;for(int i = 0;i < n;++i){sum += dist[x][i];}return sum;
}inline void solve()
{ cin >> n >> m >> k;Init(); // 初始化最短路距离数组while(m--){int a,b,c;cin >> a >> b >> c;// 记录两个点之间的最短距离,min 防止自环dist[a][b] = dist[b][a] = min(dist[a][b],c);}// 开始求各个点之间的最短距离Floyd();PII ans = {-1,-1}; // 答案城市编号,已经答案城市到各个点之间的最短距离之和while(k--){int a;cin >> a; // 获取城市编号点int distSum = DistSum(a); // 求最短距离之和if(ans.x == -1) ans = {a,distSum}; // 记录第一个点else if(ans.y > distSum) ans = {a,distSum}; // 更新更短的最短距离之和的点做 交通枢纽}// 输出答案cout << ans.x << ' ' << ans.y << endl;
}
signed main()
{
// freopen("a.txt", "r", stdin);
// ___G;int _t = 1;
// cin >> _t;while (_t--){solve();}return 0;
}最后提交:
相关文章:

最短路径专题8 交通枢纽 (Floyd求最短路 )
题目: 样例: 输入 4 5 2 0 1 1 0 2 5 0 3 3 1 2 2 2 3 4 0 2 输出 0 7 思路: 由题意,绘制了该城市的地图之后,由给出的 k 个编号作为起点,求该点到各个点之间的最短距离之和最小的点是哪个,并…...
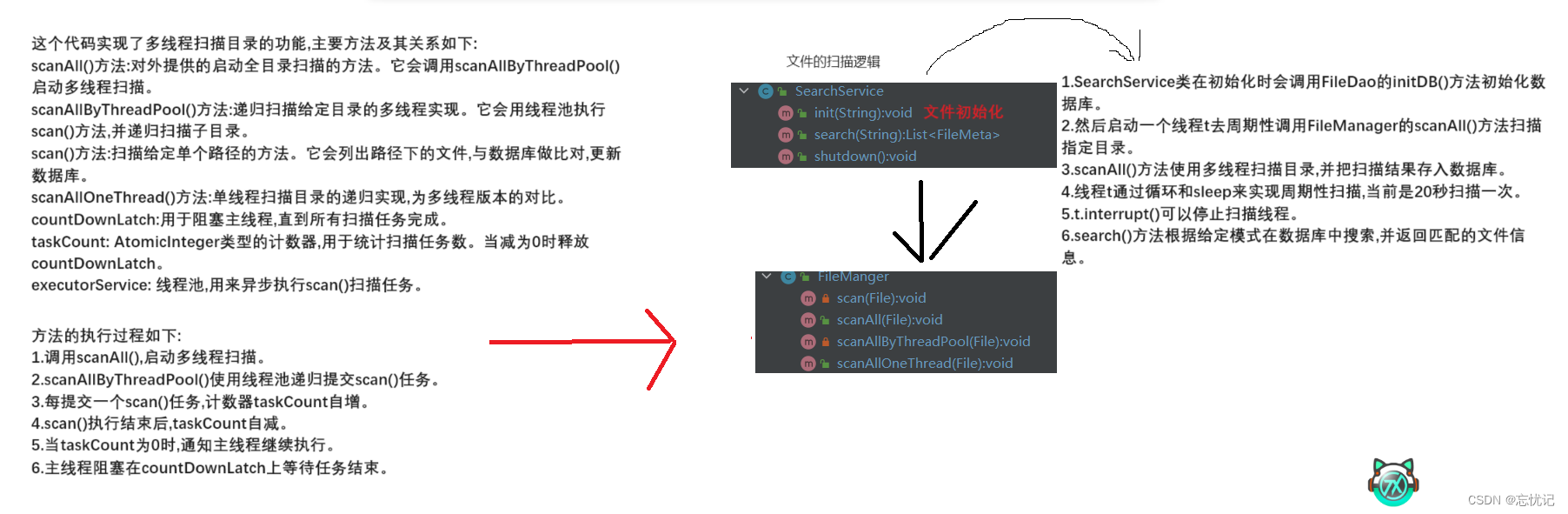
文件扫描模块
文章目录 前言文件扫描模块设计初级扫描方案一实现单线程扫描整合扫描步骤 设计初级扫描方案二周期性扫描 总结 前言 我们这个模块考虑的是数据库里面的内容从哪里获取。 获取完成后,这时候,我们就需要把目录里面文件/子文件都获取出来,并存入数据库。 文件扫描模…...
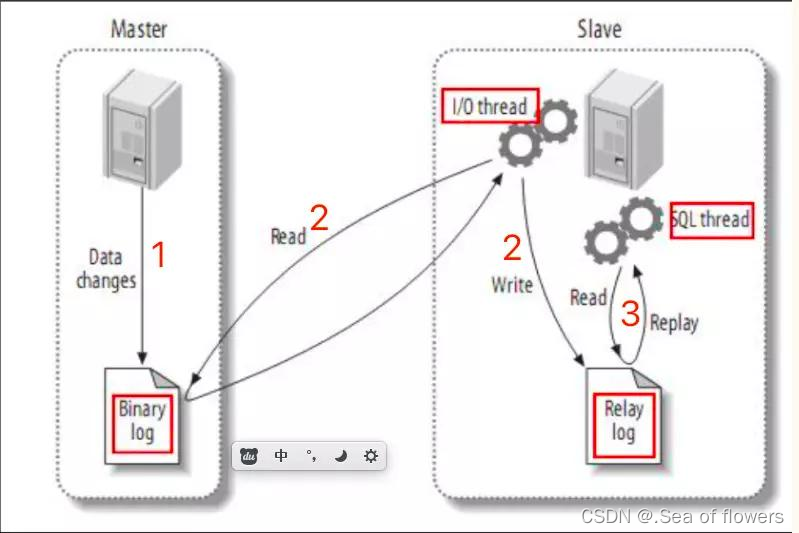
MySQL之主从复制
概述: 将主库的数据 变更同步到从库,从而保证主库和从库数据一致。 它的作用是 数据备份,失败迁移,读写分离,降低单库读写压力 原理: 主服务器上面的任何修改都会保存在二进制日志( Bin-log日志…...

[leetcode 单调栈] 901. 股票价格跨度 M
设计一个算法收集某些股票的每日报价,并返回该股票当日价格的 跨度 。 当日股票价格的 跨度 被定义为股票价格小于或等于今天价格的最大连续日数(从今天开始往回数,包括今天)。 例如,如果未来 7 天股票的价格是 [100…...

Java线程池:并发编程的利器
Java线程池:并发编程的利器 在多任务、高并发的时代,Java并发编程显得尤为重要。其中,Java线程池是一种高效的管理线程的工具,能够提高应用程序的性能和响应速度。本文将深入探讨Java线程池的工作原理、应用场景以及简单示例&…...

ARM硬件断点
hw_breakpoint 是由处理器提供专门断点寄存器来保存一个地址,是需要处理器支持的。处理器在执行过程中会不断去匹配,当匹配上后则会产生中断。 内核自带了硬件断点的样例linux-3.16\samples\hw_breakpoint\data_breakpoint.c static void sample_hbp_h…...
)
Java使用WebSocket(基础)
准备一个html页面 <!DOCTYPE HTML> <html> <head><meta charset"UTF-8"><title>WebSocket Demo</title> </head> <body><input id"text" type"text" /><button onclick"send()&…...

图像处理与计算机视觉--第五章-图像分割-自适应阈值分割
文章目录 1.自适应阈值分割介绍2.自适应阈值函数参数解析3.高斯概率函数介绍4.自适应阈值分割核心代码5.自适应阈值分割效果展示6.参考文章及致谢 1.自适应阈值分割介绍 在图片处理过程中,针对铺前进行二值化等操作的时候,我们希望能够将图片相应区域内所…...
记一次问题排查
1785年,卡文迪许在实验中发现,把不含水蒸气、二氧化碳的空气除去氧气和氮气后,仍有很少量的残余气体存在。这种现象在当时并没有引起化学家的重视。 一百多年后,英国物理学家瑞利测定氮气的密度时,发现从空气里分离出来…...
【Spring Boot】创建一个 Spring Boot 项目
创建一个 Spring Boot 项目 1. 安装插件2. 创建 Spring Boot 项目3. 项目目录介绍和运行注意事项 1. 安装插件 IDEA 中安装 Spring Boot Helper / Spring Assistant / Spring Initializr and Assistant插件才能创建 Spring Boot 项⽬ (有时候不用安装,直…...

flutter中使用缓存
前言 在flutter项目中使用ListView或者PageView等有滚动条组件的时候,切换页面的时候,再切换回来会丢失之前的滑动状态,这个时候就需要需要使用缓存功能 缓存类 import package:flutter/material.dart;class KeepAliveWrapper extends Sta…...
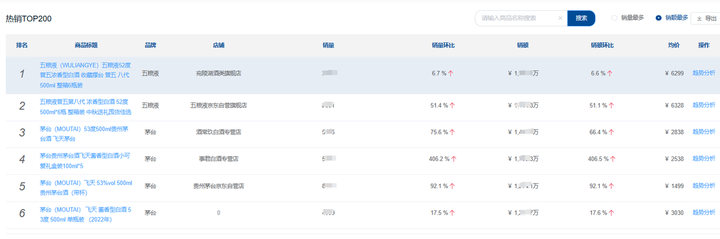
京东数据分析平台:9月中上旬白酒消费市场数据分析
9月份,围绕白酒的热点不断。9月5日,瑞幸咖啡官微发布消息称,瑞幸与贵州茅台跨界合作推出的酱香拿铁刷新单品纪录,首日销量突破542万杯,销售额破1亿元。9月14日,贵州茅台官微发布消息称与德芙推出联名产品“…...

Linux安装 spark 教程详解
目录 一 准备安装包 二 安装 scala 三 修改配置文件 1)修改 workers 文件 2)修改 spark-env.sh文件 四 进入 spark 交互式平台 一 准备安装包 可以自行去 spark 官网下载想要的版本 这里准备了 spark3.1.2的网盘资源 链接: https://pan.baidu.com…...
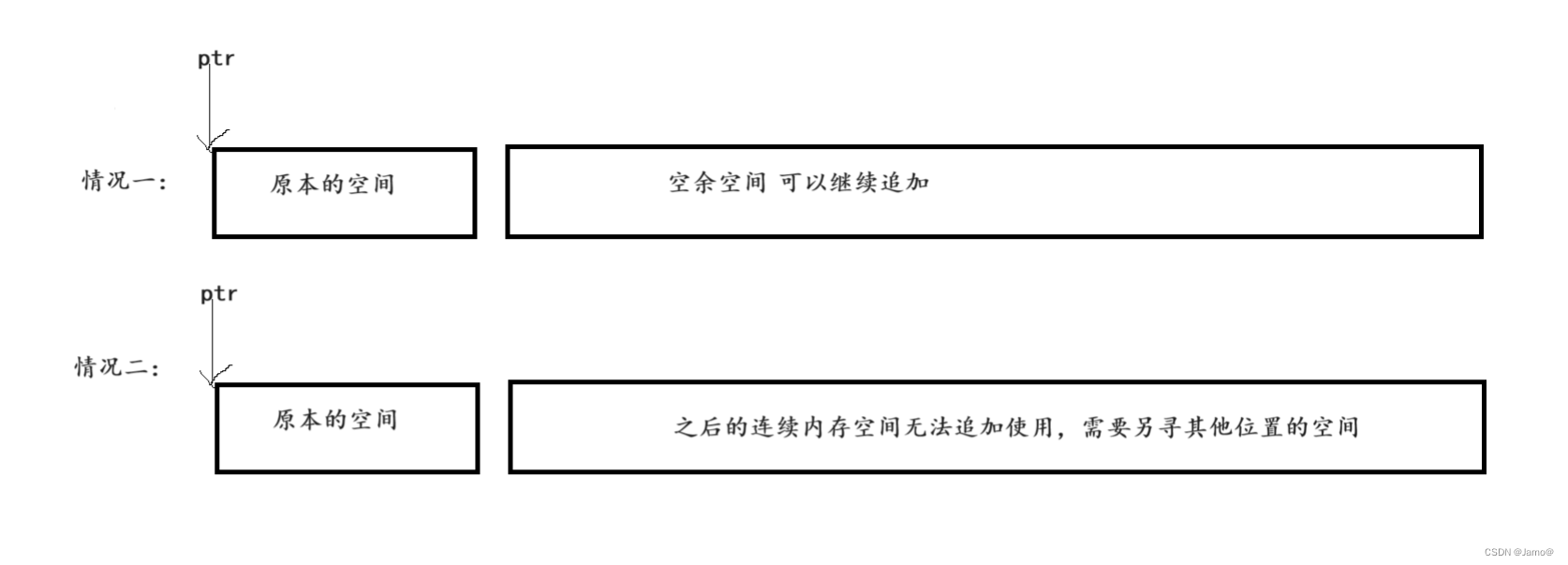
动态内存管理函数(malloc,calloc,realloc,free)
动态内存函数 1.1malloc和free C语言提供了一个动态内存开辟的函数: void* malloc (size_t size); 这个函数向内存申请一块连续可用的空间,并返回指向这块空间的指针。 如果开辟成功,则返回一个指向开辟好空间的指针。如果开辟失败&#…...

云表|都有生产管理模块,MES和ERP有什么不同,该如何选择
MES和ERP是生产制造领域的两大知名系统,虽然早已声名鹊起,但仍有不少人难以明确区分两者的差异。下面将详细阐述这两个系统的不同之处。首先,要了解MES和ERP的定义。 MES系统:全称制造执行系统(Manufacturing Executio…...

C语言 - 数组
目录 1. 一维数组的创建和初始化 1.1 数组的创建 1.2 数组的初始化 1.3 一维数组的使用 1.4 一维数组在内存中的存储 2. 二维数组的创建和初始化 2.1 二维数组的创建 2.2 二维数组的初始化 2.3 二维数组的使用 2.4 二维数组在内存中的存储 3. 数组越界 4. 数组作为函数参数 4.1…...
,有什么用,不同插槽的区别?)
Vue 中的插槽(Slot),有什么用,不同插槽的区别?
Vue 中的插槽(Slot案例详解) 是一种非常有用的功能,用于组件之间的内容分发和复用。以下是关于插槽的一些重要概念: 插槽的作用: 插槽允许你将组件的内容分发到其子组件中,以实现灵活的组件复用和自定义布局。通过插槽…...
Linux登录自动执行脚本
一、所有用户每次登录时自动执行。 1、在/etc/profile文件末尾添加。 将启动命令添加到/etc/profile文件末尾。 2、在/etc/profile.d/目录下添加sh脚本。 在/etc/profile.d/目录下新建sh脚本,设置每次登录自动执行脚本。有用户登录时,/etc/profile会遍…...

架构方法、模型、范式、治理
从架构方法、模型、范式、治理等四个方面介绍架构的概念和方法论、典型业务场景下的架构范式、不同架构的治理特点这3个方面的内容...

Linux 安全 - 内核提权
文章目录 前言一、简介1.1 prepare_creds1.2 commit_creds 二、demo参考资料 前言 在这篇文章:Linux 安全 - Credentials 介绍了 Task Credentials 相关的知识点,接下来给出一个内核编程提权的例程。 一、简介 内核模块提权主要借助于 prepare_creds …...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...
