冒泡排序和选择排序
目录
一、冒泡排序
1.冒泡排序的原理
2.实现冒泡排序
1.交换函数
2.单躺排序
3.冒泡排序实现
4.测试
5.升级冒泡排序
6.升级版代码
7.升级版测试
二、选择排序
1.选择排序的原理
2.实现选择排序
1.单躺排序
2.选择排序实现
3.测试
4.修改
5.测试
一、冒泡排序
1.冒泡排序的原理
1.从尾部开始比较相邻的两个元素,如果尾部的元素比前面的大,就交换两个元素的位置。这种方法是排升序的,想排降序的话,一旦尾部的元素比前面的小就交换即可
比方说,我有一个数组,里面存放的是9 6 3,这三个数字,我的尾部是下标为0的数,也就是9,往下走遇到了6,9比6大,所以交换,数组就会变为6 9 3
2.往前对每个相邻的元素都做这样的比较和交换,未排序中最大(最小)的那个数就会被排到未排序的数的最后
2.实现冒泡排序
1.交换函数
通过原理的讲解不难看出,冒泡排序要实现多次的交换,因此我们可以写一个简单的交换函数
void Swap(int* x, int* y)
{int tmp = *x;//创建中间变量储存x*x = *y;*y = tmp;
}2.单躺排序
void BobbleSort(int* arr, int n)
//传递数组和数组元素个数
{int j = 0;for (j = 0; j < n - 1; j++)//j<n-1避免越界{if (arr[j] > arr[j + 1])//不断地进行比较,一遇到大的就进行交换,会将最大的数移动到数组的最后{Swap(&arr[j + 1], &arr[j]);}}
}3.冒泡排序实现
一趟排好一个数,那么我们一共有n个数,那么循环次数就可以修改成n次
void BobbleSort(int*arr,int n)
//传递数组和数组元素个数
{int i = 0;int j = 0;for (i = 0; i < n; i++)//n次排序排n个数{for (j = 0; j < n - 1; j++)//j<n-1避免越界{if (arr[j] > arr[j + 1])//不断地进行比较,一遇到大的就进行交换,会将最大的数移动到数组的最后{Swap(&arr[j + 1], &arr[j]);}}}
}4.测试
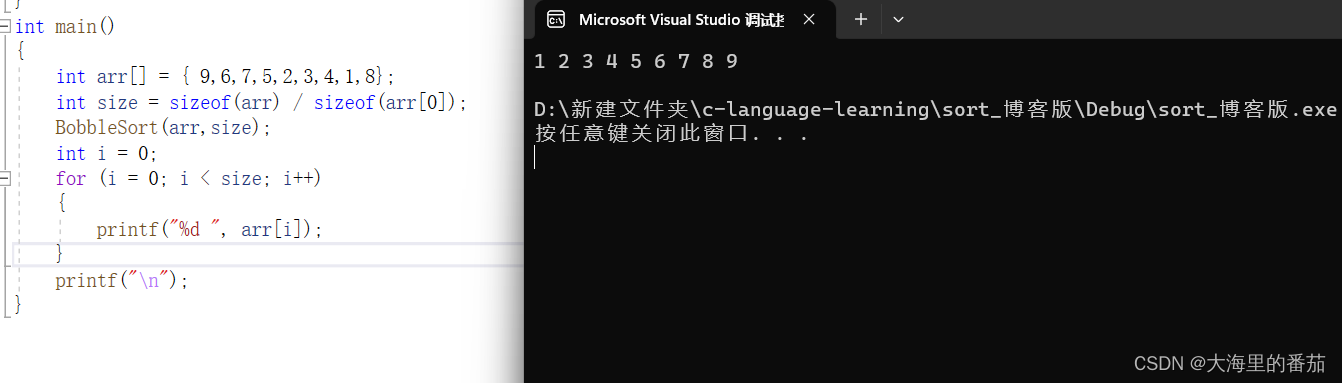
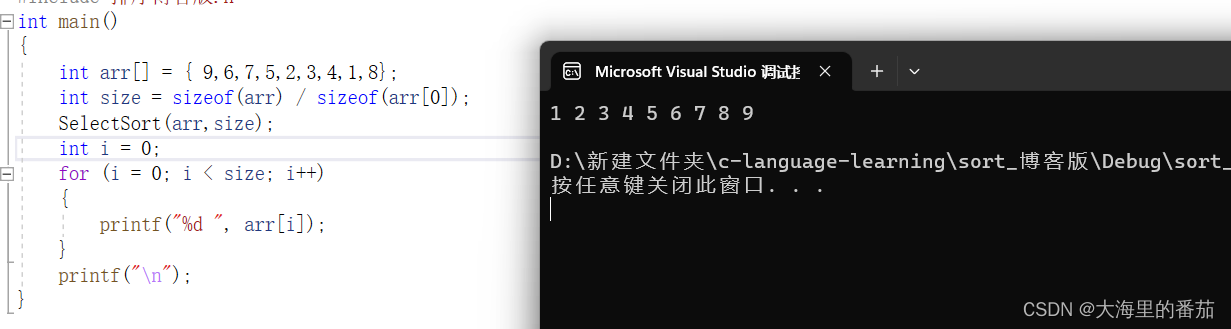
int main()
{int arr[] = { 9,6,7,5,2,3,4,1,8};int size = sizeof(arr) / sizeof(arr[0]);BobbleSort(arr,size);int i = 0;for (i = 0; i < size; i++){printf("%d ", arr[i]);}printf("\n");
}
5.升级冒泡排序
1.我们可以看出,每次我们进行完一趟排序后,未排序中最大(最小)的那个数就会被排到未排序的数的最后,因此我们没有必要去和那些已经排好序的数作比较,所以我们可以把单躺循环判断语句改写成j<n-i-1,i代表已经排好序的数的个数,减去i就可以避免与这些数重复的比较。
2.如果数组已经有序我们还在比较显然就会浪费大量的时间 可以看出,如果数组无序的话,那个未排序中最大(最小)的那个数就会被排到未排序的数的最后,期间一定会出现交换,而如果有序的话就一定不会出现交换。
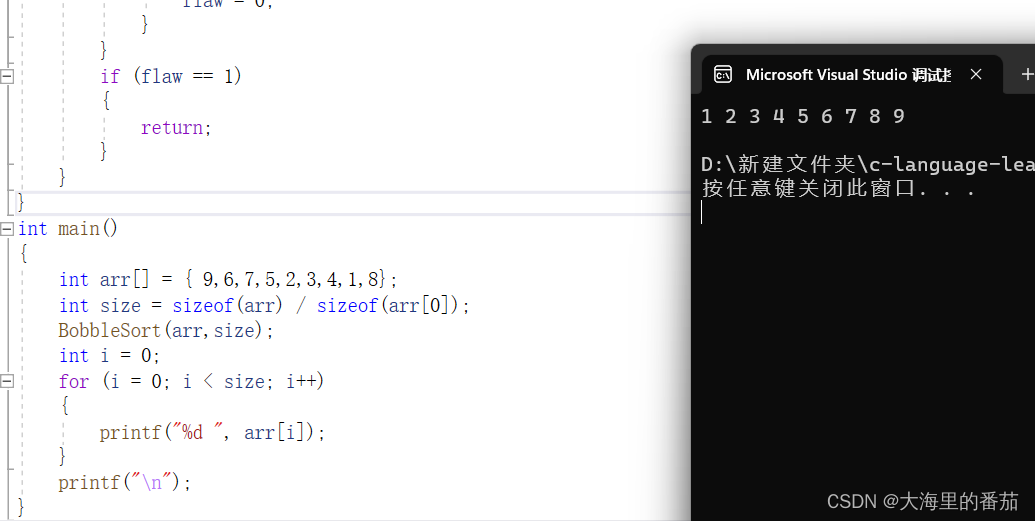
因此我们可以通过一个flaw变量来实现,每次进行新的一趟排序前,先将flaw变量初始化为1,一旦发生交换就令它为0,再在最外面根据flaw来判断是否发生了交换,如果发生了交换,那么数组依然无序,若是没有,则有序,结束函数
6.升级版代码
void BobbleSort(int*arr,int n)
//传递数组和数组元素个数
{int i = 0;int j = 0;for (i = 0; i < n; i++)//n次排序排n个数{int flaw = 1;for (j = 0; j < n -i- 1; j++)//j<n-1避免越界{if (arr[j] > arr[j + 1])//不断地进行比较,一遇到大的就进行交换,会将最大的数移动到数组的最后{Swap(&arr[j + 1], &arr[j]);flaw = 0;}}if (flaw == 1){return;}}
}7.升级版测试
二、选择排序
1.选择排序的原理
选择排序十分的简单粗暴,就是在数组中找到最大值和最小值,然后把它们放到对应的位置,如果你想排升序最大值放右边,最小值放左边,排降序相反即可。
2.实现选择排序
1.单躺排序
第一趟排序我们找到最大值和最小值然后把它们放在对应的位置即可
void SelectSort(int*arr,int n)
{int max = 0;int min = 0;//max和min均储存下标int i = 0;for (i = 0; i < n; i++){if (arr[max] < arr[i]){max = i;}if (arr[min] > arr[i]){min = i;}}Swap(&arr[0] = &arr[min]);//将最小值放到最前面Swap(&arr[n-1],&arr[max]);//将最大值放到最后}2.选择排序实现
思考要排几趟,可以看出,每次都会将最大和最小的排到对应的位置,那么,循环差不多就是for(j=0;j<n/2;j++); 但要不要带上等号呢。这个可以代入实例进行思考,比方说,一共有5个元素,你要给它进行两次排序即可,而5/2=2,j<2,进行2次循环,满足条件,一共有6个元素,要进行三次排序,6/2*3,j<3,进行3次循环,满足条件。奇偶数均检验,故无需带上等于号。
思考细节,每比较一次,我们需要比较的区间就会缩小。所以应将查找最大最小的循环修改成for(i=j;i<n-j;i++); 同理,max和min的下标也不能一直都是0,区间减小了,你却使用到区间之外的数,显然不对,max,min应初始化为j
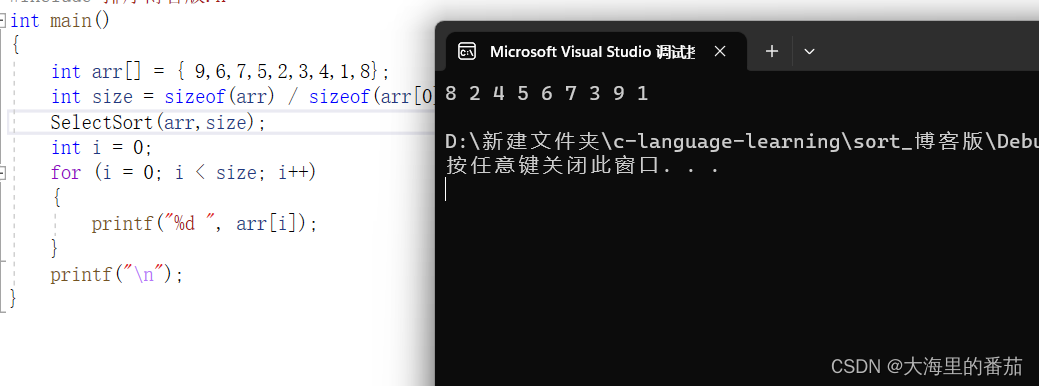
void SelectSort(int* arr, int n)
{int i = 0; int j = 0;for (j = 0; j < n / 2; j++){int max = j; int min = j;//max和min均储存下标for (i = j; i < n - j; i++){if (arr[max] < arr[i]){max = i;}if (arr[min] > arr[i]){min = i;}}Swap(&arr[j], &arr[min]);//将最小值放到最前面Swap(&arr[n - 1 - j], &arr[max]);//将最大值放到最后}
}3.测试
 4.修改
4.修改
为什么会出错呢,仔细思考,你会发现,若是max和j相等的话,j先和min进行交换,那么此时的j就不再是最大值的下标了,自然会出错,因此,当max和j相等的时候,应该在交换之后使max更新为min,更新到真正最大值的下标。
void SelectSort(int* arr, int n)
{int i = 0; int j = 0;for (j = 0; j <n / 2; j++){int max = j; int min = j;//max和min均储存下标for (i = j; i < n-j; i++){if (arr[max] < arr[i]){max = i;}if (arr[min] > arr[i]){min = i;}}Swap(&arr[j], &arr[min]);//将最小值放到最前面if (j == max)//更新{max = min;}Swap(&arr[n - 1 - j], &arr[max]);//将最大值放到最后}
}5.测试
至此,冒泡排序和选择排序讲解完成,感谢各位友友的来访,祝各位友友前程似锦O(∩_∩)O
相关文章:

冒泡排序和选择排序
目录 一、冒泡排序 1.冒泡排序的原理 2.实现冒泡排序 1.交换函数 2.单躺排序 3.冒泡排序实现 4.测试 5.升级冒泡排序 6.升级版代码 7.升级版测试 二、选择排序 1.选择排序的原理 2.实现选择排序 1.单躺排序 2.选择排序实现 3.测试 4.修改 5.测试 一、冒泡排序…...
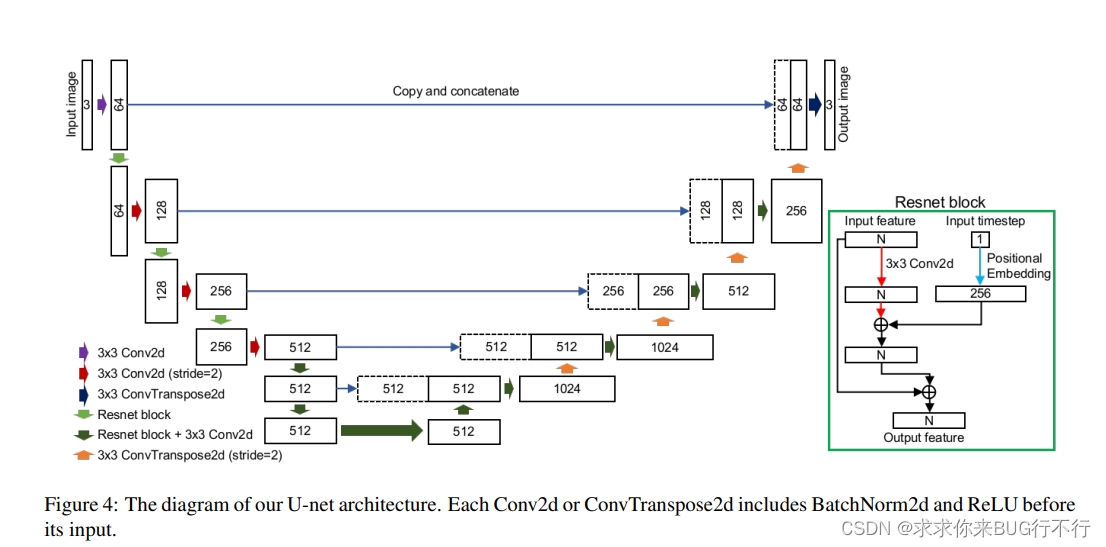
【深度学习】UNIT-DDPM核心讲解
文章目录 大致介绍:扩散损失:转换损失:循环一致性损失:推理过程:优缺点: 参考文章: https://blog.csdn.net/ssshyeong/article/details/127210086 这篇文章对整个文章 UNIT-DDPM: UNpaired Imag…...

Java 线程的优先级
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开兴好久好久😎 📚系列专栏:Java全栈,…...

金融数学方法:牛顿法
目录 1.牛顿法1.1 牛顿法介绍1.2 算法步骤 2. 具体算例3.总结 1.牛顿法 1.1 牛顿法介绍 牛顿法(Newton’s method),也被称为牛顿-拉夫森方法(Newton-Raphson method),是一种用于数值逼近根的迭代方法。它是…...

MongoTemplate | 多条件查询
MongoTemplate查询 Resource private MongoTemplate mongoTemplate;public <T> List<T> getDataList(String param1, Long param2, Class<T> clazz) {// 构建queryQuery query constructQuery(param1, param2);// 查询return mongoTemplate.find(query, cl…...

优秀程序员是怎么思考的?
首发日更公 Z 号:十二又十三 作为一名优秀的程序员,思考是我们工作中最重要的一部分。它不仅能够帮助我们解决问题,还能够提升我们的技术水平和职业发展。那么,优秀程序员是如何思考的呢?本文将为您介绍一个思考框架和…...

【juc】countdownlatch实现游戏进度
目录 一、截图示例二、代码示例 一、截图示例 二、代码示例 package com.learning.countdownlatch;import java.util.Arrays; import java.util.Random; import java.util.concurrent.CountDownLatch; import java.util.concurrent.ExecutorService; import java.util.concurr…...

Spring Webflux HttpHandler源码整理
HttpHandler的构造 自动启动配置类:HttpHandlerAutoConfigurationBean public HttpHandler httpHandler(ObjectProvider<WebFluxProperties> propsProvider) {HttpHandler httpHandler WebHttpHandlerBuilder.applicationContext(this.applicationContext).…...
Qt扩展-Advanced-Docking 简介及配置
Advanced-Docking 简介及配置 一、概述二、项目结构三、安装配置四、代码测试 一、概述 Advanced-Docking 是类似QDockWidget 功能的多窗口停靠功能的库。很像visual stdio 的 停靠功能,这个库对于停靠使用的比较完善。很多的软件都使用了这个框架。 项目源地址&a…...

Decorator
Decorator 动机 在某些情况下我们可能会“过度地使用继承来扩展对象的功能”, 由于继承为类型引入的静态特质,使得这种扩展方式缺乏灵活性; 并且随着子类的增多(扩展功能的增多),各种子类的组合ÿ…...
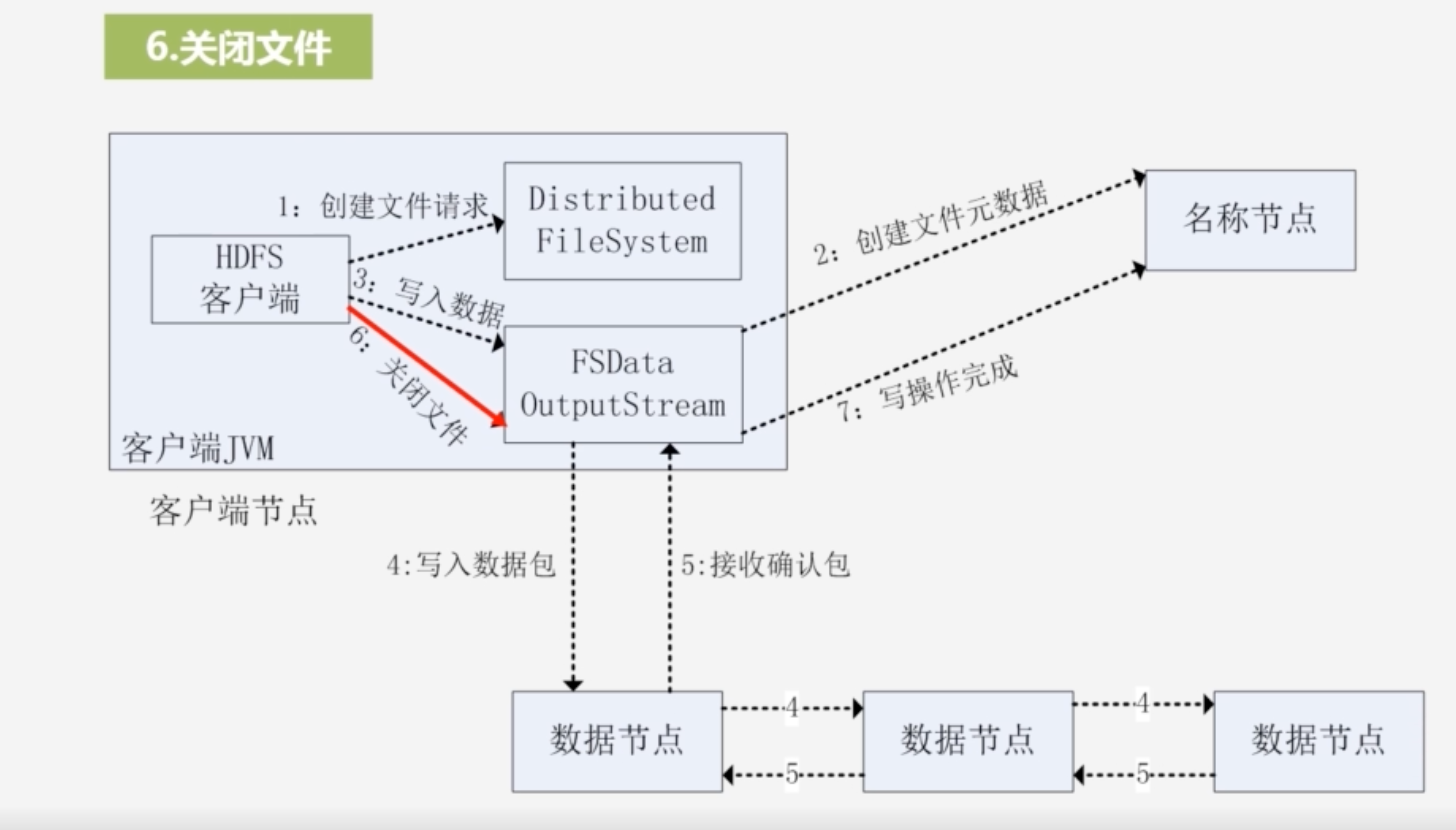
分布式文件系统HDFS(林子雨慕课课程)
文章目录 3. 分布式文件系统HDFS3.1 分布式文件系统HDFS简介3.2 HDFS相关概念3.3 HDFS的体系结构3.4 HDFS的存储原理3.5 HDFS数据读写3.5.1 HDFS的读数据过程3.5.2 HDFS的写数据过程 3.6 HDFS编程实战 3. 分布式文件系统HDFS 3.1 分布式文件系统HDFS简介 HDFS就是解决海量数据…...

CSS中:root伪类的使用
在CSS中,:root是一个伪类选择器,它选择的是文档树的根元素。在HTML文档中,这个根元素通常是<html>。:root伪类选择器常常被用于定义全局的CSS变量或者设置全局的CSS样式。 例如,你可以使用:root来定义一个全局的字体大小&a…...
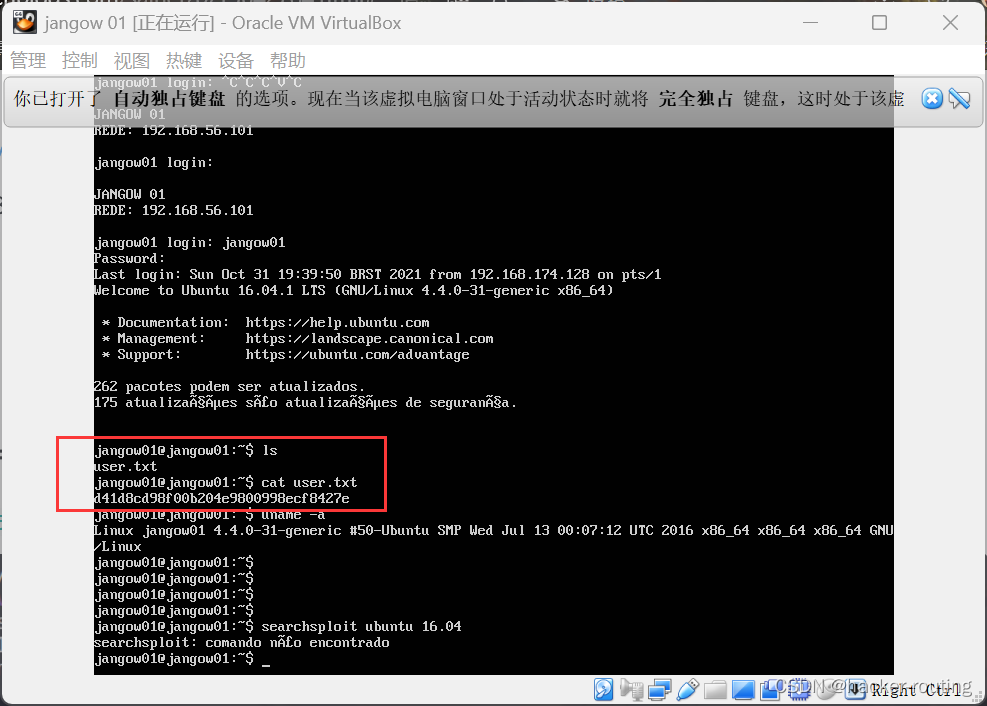
VulnHub JANGOW
提示(主机ip分配问题) 因为直接在VulnHub上下载的盒子,在VMware上打开,默认是不分配主机的 所以我们可以在VirtualBox上打开 一、信息收集 发现开放了21和80端口,查看一下80端口 80端口: 检查页面后发现…...

OpenMesh 获取网格面片各个顶点
文章目录 一、简介二、实现代码三、实现效果一、简介 OpenMesh中有很多循环器,这里便是其中一种面顶点循环器,以此来获得面片的各个顶点。 二、实现代码 #define _USE_MATH_DEFINES #include <iostream> #include <unordered_map>...

【前端设计模式】之原型模式
原型模式特性 原型模式(Prototype Pattern)是一种创建型设计模式,它通过克隆现有对象来创建新对象,而不是通过实例化类。原型模式的主要特性包括: 原型对象:原型对象是一个已经存在的对象,它作…...

软件设计原则
设计原则 一、单一原则 1. 如何理解单一职责原则 单一职责原则(Single Responsibility Principle,简称SRP),它要求一个类或模块应该只负责一个特定的功能。实现代码的高内聚和低耦合,提高代码的可读性和可维护性。 …...
【面试HOT100】哈希双指针滑动窗口
系列综述: 💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于LeetCodeHot100进行的,每个知识点的修正和深入主要参考…...
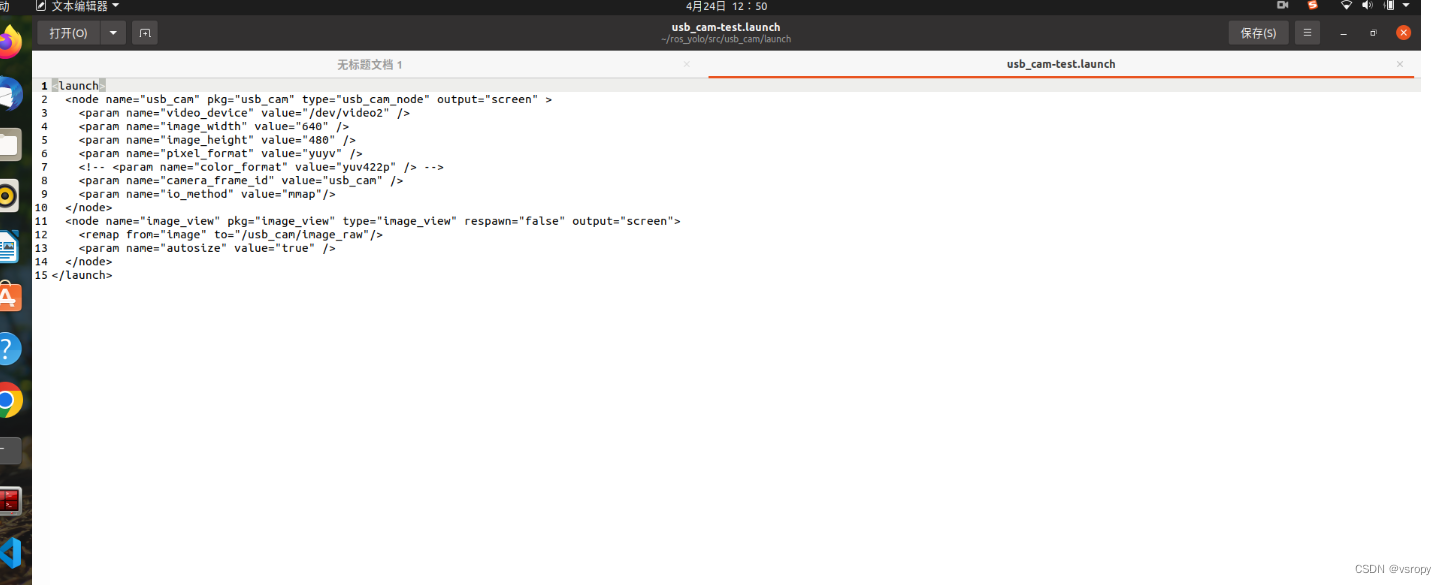
Ubuntu20.04 配置 yolov5_ros 功能包记录
文章目录 本文参考自博主源801,结合自己踩坑后修改 项目地址:https://github.com/mats-robotics/yolov5_ros 1.新建工作空间 新建一个工作空间 yolo_ros(名字可自定义),在 yolo_ros 下新建文件夹 src 并catkin_make进行编译 2. 安装相机驱动,可以选用较为主流的 usb_cam 或…...
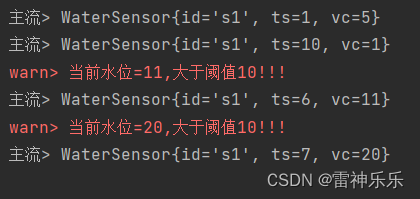
Flink的处理函数——processFunction
目录 一、处理函数概述 二、Process函数分类——8个 (1)ProcessFunction (2)KeyedProcessFunction (3)ProcessWindowFunction (4)ProcessAllWindowFunction ÿ…...

Linux系统中的ps命令详解及用法介绍
文章目录 一、介绍ps命令A. ps命令的作用B. ps命令的参数 二、常见的ps命令用法A. 显示所有进程信息B. 显示指定进程信息C. 显示指定用户的进程信息D. 按CPU使用率排序显示进程信息E. 按内存使用率排序显示进程信息 三、进一步了解ps命令A. 显示进程树信息B. 显示线程和进程关系…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...