刷题笔记28——一直分不清的Kruskal、Prim、Dijkstra算法
图算法刷到这块,感觉像是走了一段黑路快回到家一样,看到这三个一直分不太清总是记混的名字,我满脑子想起的是大学数据结构课我坐在第一排,看着我班导一脸无奈,心想该怎么把这个知识点灌进木头脑袋里边呢。有很多算法我当时想不明白,感觉这样不对劲,这咋变一变就能找到么。但是现在想来,当时确实没必要想得太明白,如果我早知道这些知识在过了短短一两年之后我又会以陌生人的身份重新认识他们,当时就该转过头去,和我舍友大聊特聊离谱的八卦,让谢导早点放弃教会我们这个想法。
- 生成树就是在图中找到一棵包含图中所有节点的树
- 生成树是含有图中所有顶点的无环连通子图
- 所有可能的生成树中,权重和最小的那棵生成树就叫「最小生成树」
1584. 连接所有点的最小费用Kruskal
class Solution {public int minCostConnectPoints(int[][] points) {int n = points.length;List<Edge> edges = new ArrayList<Edge>();DisjoinSetUnion dsu = new DisjoinSetUnion(n);for(int i=0;i<n;i++){for(int j=i+1;j<n;j++){edges.add(new Edge(i,j,dist(points,i,j)));} }// 升序Collections.sort(edges, new Comparator<Edge>() {public int compare(Edge edge1, Edge edge2) {return edge1.weight - edge2.weight;}});int ret = 0; int num = 0;for(Edge edge:edges){int x = edge.start;int y = edge.end;int weight = edge.weight;if(dsu.unionSet(x,y)){ret += weight;num++;if(num==n-1){break;}}}return ret;}public int dist(int[][] points,int i,int j){int weight = Math.abs(points[i][0]-points[j][0]) + Math.abs(points[i][1]-points[j][1]);return weight;}
}class DisjoinSetUnion{int[] parent;int[] rank;int n;public DisjoinSetUnion(int n){this.n = n;this.rank = new int[n];Arrays.fill(this.rank,1);this.parent = new int[n];for(int i=0;i<n;i++){this.parent[i] = i;}}public int find(int x){if(parent[x]!=x){parent[x] = find(parent[x]);}return parent[x];}public boolean unionSet(int x, int y){int px = find(x);int py = find(y);// 是连通的,当节点联通后就会有共同的parent,说明这两个点已经被加入到树中了,没加入的话parent是自身if(px == py){return false;}else{if(rank[px]<rank[py]){int temp = px;px = py;py = temp;}rank[px] += rank[py];parent[py] = px;return true; }}
}class Edge{int start;int end;int weight;public Edge(int start,int end,int weight){this.start = start;this.end = end;this.weight = weight;}
}1584. 连接所有点的最小费用Prim
class Solution {public int minCostConnectPoints(int[][] points) {int n = points.length;List<int[]>[] graph =buildGraph(n,points);Prim prim = new Prim(graph);int ret = prim.weightSum();return ret;}List<int[]>[] buildGraph(int n,int[][] points){List<int[]>[] graph = new LinkedList[n];for(int i=0;i<n;i++){graph[i] = new LinkedList<int[]>();}for(int i=0;i<n;i++){for(int j=i+1;j<n;j++){int xi = points[i][0]; int yi = points[i][1];int xj = points[j][0]; int yj = points[j][1];int weight = Math.abs(xi-xj) + Math.abs(yi-yj);graph[i].add(new int[]{i,j,weight});graph[j].add(new int[]{j,i,weight});}}return graph;}
}class Prim{private PriorityQueue<int[]> pq;private boolean[] inMST;private int weightSum = 0;private List<int[]>[] graph;public Prim(List<int[]>[] graph){this.graph = graph;this.pq = new PriorityQueue<>((a,b)->{return a[2]-b[2];});int n = graph.length;this.inMST = new boolean[n];// 将0节点的所有的边加入到pq中cut(0);inMST[0] = true;while(!pq.isEmpty()){int[] edge = pq.poll();int to = edge[1];int weight = edge[2];if(inMST[to]){continue;}cut(to);inMST[to] = true;weightSum += weight;}}private void cut(int n){List<int[]> edges = graph[n];for(int[] edge:edges){if(inMST[edge[1]]){continue;}pq.offer(edge);}}public int weightSum(){return weightSum;}public boolean allConnected(){for(int i=0;i<inMST.length;i++){if(!inMST[i]) return false;}return true;}
}743. 网络延迟时间 dijkstra
class Solution {public int networkDelayTime(int[][] times, int n, int k) {List<int[]>[] graph = new LinkedList[n+1];for(int i=1;i<n+1;i++){graph[i] = new LinkedList<>();}for(int[] time:times){int from = time[0];int to = time[1];int len = time[2];graph[from].add(new int[]{to,len});}int[] distTo = dijkstra(k,graph);int maxtime = 0;for(int i=1;i<n+1;i++){if(distTo[i] == Integer.MAX_VALUE){return -1;}maxtime = Math.max(distTo[i],maxtime);}return maxtime;}int[] dijkstra(int start, List<int[]>[] graph){int n = graph.length;int[] distTo = new int[n];Arrays.fill(distTo,Integer.MAX_VALUE);//给定初始化距离distTo[start] = 0;Queue<State> pq = new PriorityQueue<>((a,b)->{return a.distFromStart- b.distFromStart;});pq.offer(new State(start,0));while(!pq.isEmpty()){State curnode = pq.poll();int nodeId = curnode.id;int distFromStart = curnode.distFromStart;// 如果这条路径没有改变那就不需要对该路径的邻接节点进行更新if(distFromStart>distTo[nodeId]){continue;}for(int[] adjnode:graph[nodeId]){int to =adjnode[0];int len =adjnode[1];// 经过曲折之后的路径小于原始的最初设定if(distFromStart+len < distTo[to]){distTo[to] = distFromStart+len;pq.offer(new State(to,distFromStart+len));}}}return distTo;}
}class State{int id;int distFromStart;State(int id, int distFromStart) {this.id = id;this.distFromStart = distFromStart;}
}
1631. 最小体力消耗路径
class Solution {public int minimumEffortPath(int[][] heights) {int n = heights.length*heights[0].length;List<int[]>[] graph = new LinkedList[n];for(int i=0;i<n;i++){graph[i] = new LinkedList<>();}for(int i=0;i<heights.length;i++){for(int j=0;j<heights[0].length;j++){int loc = i*heights[0].length+j;if(i-1>-1){graph[loc].add(new int[]{i-1,j,Math.abs(heights[i][j]-heights[i-1][j])});}if(j-1>-1){graph[loc].add(new int[]{i,j-1,Math.abs(heights[i][j]-heights[i][j-1])});}if(i+1<heights.length){graph[loc].add(new int[]{i+1,j,Math.abs(heights[i][j]-heights[i+1][j])});}if(j+1<heights[0].length){graph[loc].add(new int[]{i,j+1,Math.abs(heights[i][j]-heights[i][j+1])});}}}int[] maxheight = new int[n];Arrays.fill(maxheight,Integer.MAX_VALUE);maxheight[0] = 0;Queue<State> pq = new PriorityQueue<>((a,b)->{return a.maxh-b.maxh;});pq.offer(new State(0,0,0));while(!pq.isEmpty()){State s = pq.poll();int row = s.row;int col = s.col;int maxh = s.maxh;if (row == heights.length - 1 && col == heights[0].length - 1) {return maxh;}// 到达某点找到一条更近的距离if(maxh > maxheight[row*heights[0].length+col]){continue;}for(int[] adjnode:graph[row*heights[0].length+col]){int r = adjnode[0];int c = adjnode[1];int h = adjnode[2];int temp = Math.max(maxheight[row*heights[0].length+col],h);if(temp<maxheight[r*heights[0].length+c]){maxheight[r*heights[0].length+c] = temp;pq.offer(new State(r,c,temp));}}}return -1;}
}class State{int row;int col;int maxh;State(int row,int col,int maxh){this.row = row;this.col = col;this.maxh = maxh;}
}
相关文章:

刷题笔记28——一直分不清的Kruskal、Prim、Dijkstra算法
图算法刷到这块,感觉像是走了一段黑路快回到家一样,看到这三个一直分不太清总是记混的名字,我满脑子想起的是大学数据结构课我坐在第一排,看着我班导一脸无奈,心想该怎么把这个知识点灌进木头脑袋里边呢。有很多算法我…...

Mysql时间同步设置
Mysql时间同步设置 当涉及到设置MySQL数据库时间与电脑同步时,实际的步骤可能会因操作系统和数据库版本的不同而有所差异。以下是一个基本的步骤示例,供您参考: 检查电脑时间: 首先确保电脑操作系统的时间是正确的。 设置MySQL时…...
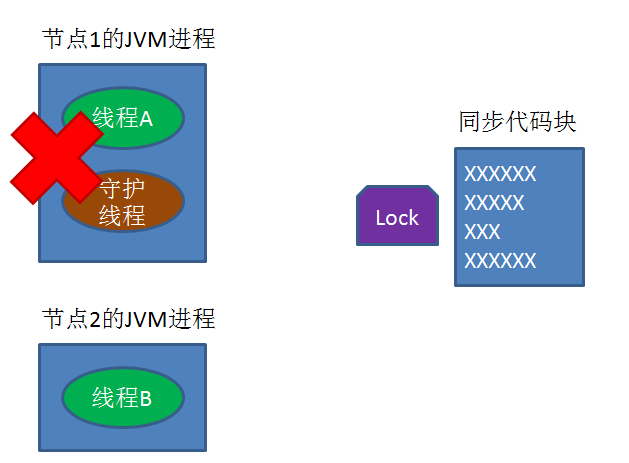
如何理解分布式锁?
分布式锁的实现有哪些? 1.Memcached分布式锁 利用Memcached的add命令。此命令是原子操作,只有在key不存在的情况下,才能add成功,也就意味着线程得到了锁。 2.Reids分布式锁 和Memcached的方式类似,利用Redis的setn…...
windows 远程连接 ubuntu桌面xrdp
更新 sudo apt update安装组件 sudo apt-get install xorg sudo apt-get install xserver-xorg-core sudo apt-get install xorgxrdp sudo apt install xfce4 xfce4-goodies xorg dbus-x11 x11-xserver-utilsxrdp sudo apt install xrdp sudo systemctl status xrdp sudo …...

数据采集时使用HTTP代理IP效率不高怎么办?
在进行数据采集时,使用HTTP代理 可以帮助我们实现隐私保护和规避封禁的目的。然而,有时候我们可能会遇到使用HTTP代理 效率不高的问题,如连接延迟、速度慢等。本文将为您分享解决这一问题的实用技巧,帮助您提高数据采集效率&#…...
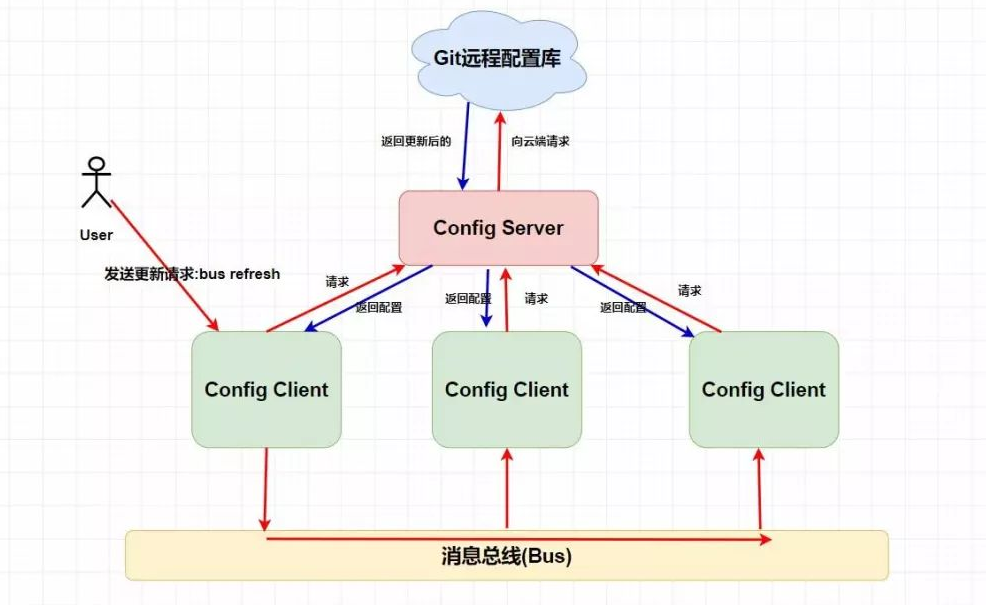
你了解的SpringCloud核心组件有哪些?他们各有什么作用?
SpringCloud 1.什么是 Spring cloud Spring Cloud 为最常见的分布式系统模式提供了一种简单且易于接受的编程模型,帮助开发人员构建有弹性的、可靠的、协调的应用程序。Spring Cloud 构建于 Spring Boot 之上,使得开发者很容易入手并快速应用于生产中。…...

【Gradle-10】不可忽视的构建分析
1、前言 构建性能对于生产力至关重要。 随着项目越来越复杂,花费在构建上的时间就越长,开发效率就越低。 通过分析构建过程,可以了解项目构建的时间都花在哪,以及项目存在哪些潜在的问题,找到构建瓶颈,解…...

2034. 股票价格波动
给你一支股票价格的数据流。数据流中每一条记录包含一个 时间戳 和该时间点股票对应的 价格 。 不巧的是,由于股票市场内在的波动性,股票价格记录可能不是按时间顺序到来的。某些情况下,有的记录可能是错的。如果两个有相同时间戳的记录出现…...

JavaScript 事件详解细节
JavaScript 事件详解细节 JavaScript 中的事件是前端开发中非常重要的一个概念。通过事件,我们可以捕捉和响应用户与网页的交互,比如点击按钮、输入文字等。这篇博客文章将详细介绍 JavaScript 中的事件,希望能帮助你更好地理解和使用这一功…...
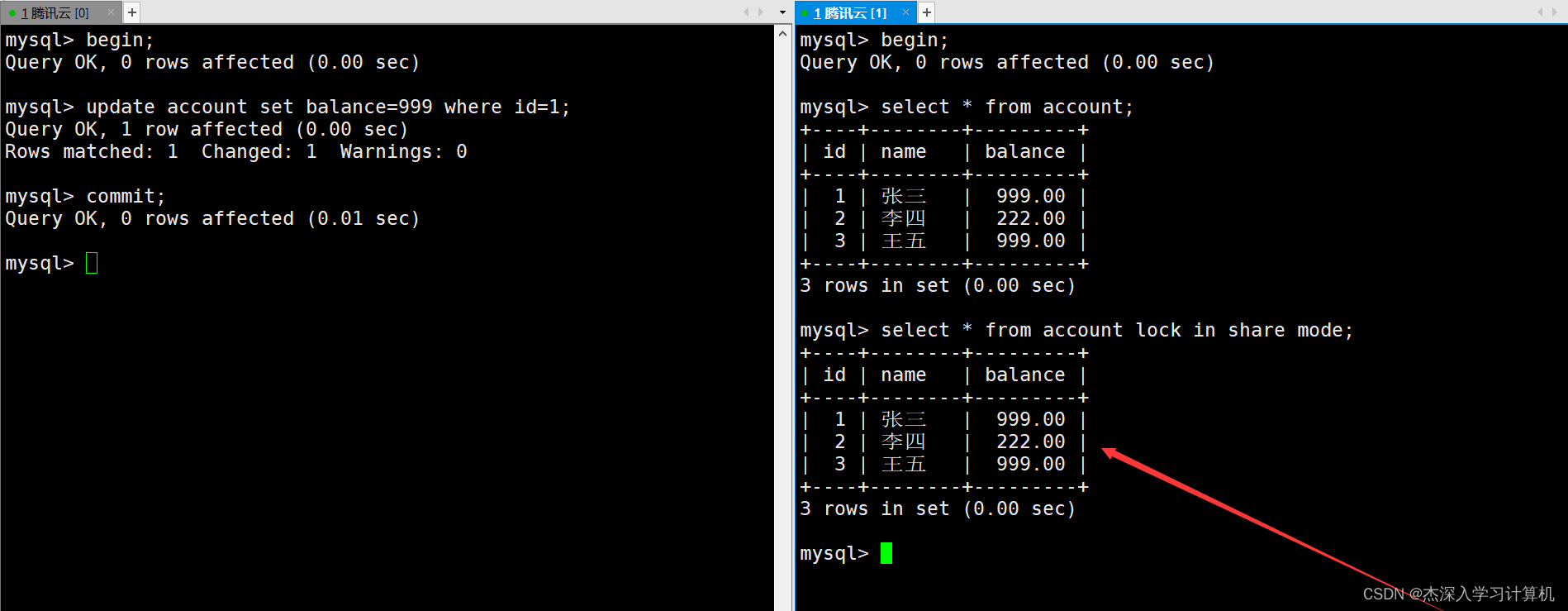
【MySQL】事务管理
目录 MySQL事务管理 事务的概念 事务的版本支持 事务的提交方式 事务的相关演示 事务的隔离级别 查看与设置隔离级别 读未提交(Read Uncommitted) 读提交(Read Committed) 可重复读(Repeatable Read…...

Git 学习笔记 | Git 基本操作命令
Git 学习笔记 | Git 基本操作命令 Git 学习笔记 | Git 基本操作命令文件的四种状态查看文件状态忽略文件 Git 学习笔记 | Git 基本操作命令 文件的四种状态 版本控制就是对文件的版本控制,要对文件进行修改、提交等操作,首先要知道文件当前在什么状态&…...
)
第五章:最新版零基础学习 PYTHON 教程—Python 字符串操作指南(第七节 - Python 中的字符串模板类)
在字符串模块中,模板类允许我们为输出规范创建简化的语法。该格式使用由 $ 和有效 Python 标识符(字母数字字符和下划线)组成的占位符名称。用大括号将占位符括起来,使其后面可以跟更多的字母数字字母,且中间不留空格。写入 $$ 会创建一个转义的 $。 Python 字符串模板:…...
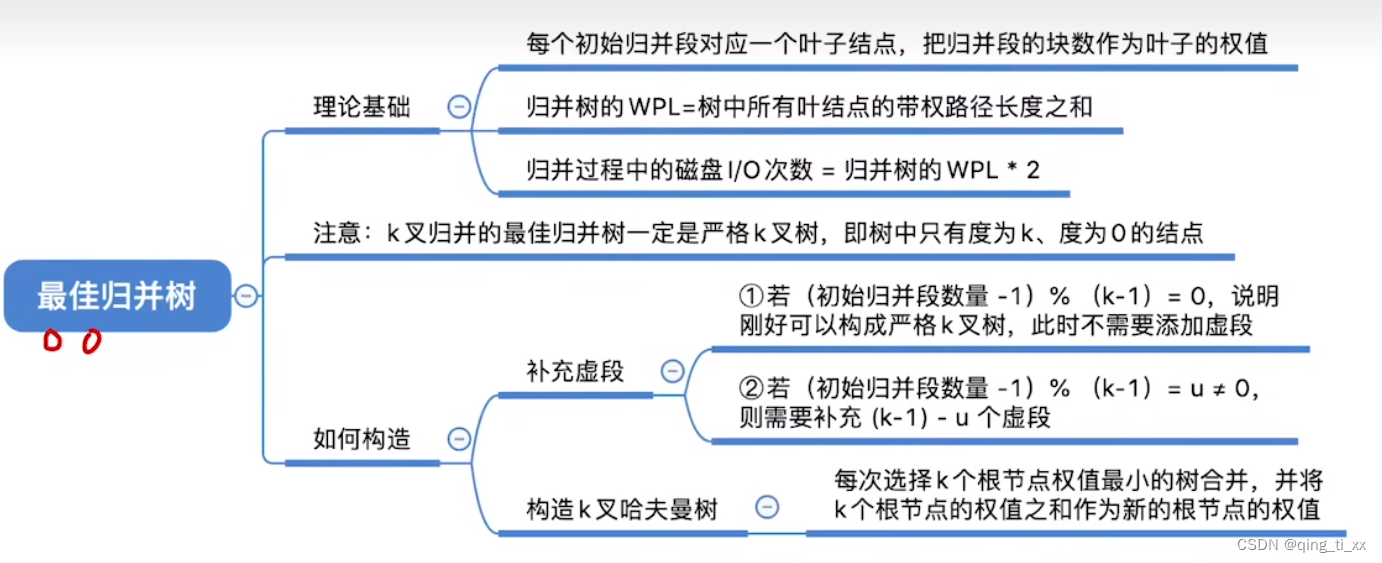
第八章 排序 十四、最佳归并树
目录 一、定义 二、多路最佳归并树 三、多路最佳归并树少了一个归并段 四、总结 一、定义 最佳归并树是指将若干个有序序列合并成一个有序序列的一种方式,使得所有合并操作的总代价最小的一棵二叉树。其中,代价通常指合并两个有序序列的操作次数或比…...

Python 中,类的方法的标准注释模板
在 Python 中,类的标准注释通常遵循以下格式: class 类名:"""类的简要描述属性:- 属性1 (类型): 属性1的描述- 属性2 (类型): 属性2的描述方法:- 方法1(): 方法1的描述- 方法2(): 方法2的描述示例:>>> 对象 类名()>>>…...
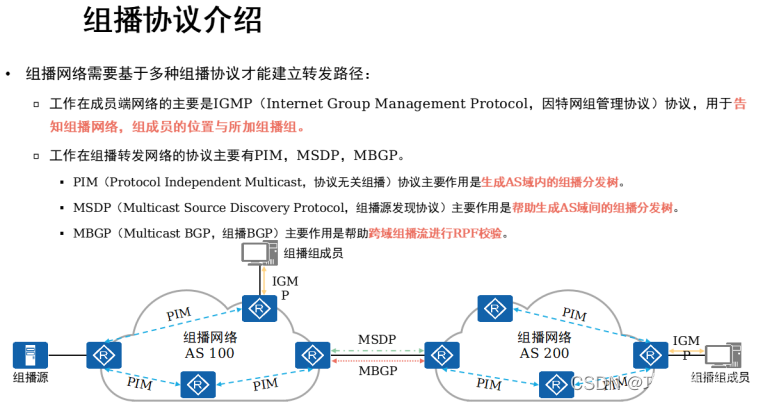
IPSG技术和IP组播
1,IPSG技术概述 实验: DHCP snooping IPSG 拓扑: 需求: 1,实现PC1 和PC2 动态获取IP地址 2, 在SW2 配置DHCP snooping 实现DHCP 服务器的安全 3, 在 连接PC 1 和 PC2 的 接口上 做IPSG ,防止终端…...

【大数据】Apache NiFi 助力数据处理及分发
Apache NiFi 助力数据处理及分发 1.什么是 NiFi ?2.NiFi 的核心概念3.NiFi 的架构4.NiFi 的性能预期和特点5.NiFi 关键特性的高级概览 1.什么是 NiFi ? 简单的说,NiFi 就是为了解决不同系统间数据自动流通问题而建立的。虽然 dataflow 这个术…...

什么是 SRE?一文详解 SRE 运维体系
目录 可观测性系统 故障响应 故障复盘 测试与发布 容量规划 自动化工具开发 用户体验 可观测性系统 在任何有一定规模的企业内部,一旦推行起来整个SRE的运维模式,那么对于可观测性系统的建设将变得尤为重要,而在整个可观测性系统中&a…...
【Docker】初识 Docker,Docker 基本命令的使用,Dockerfile 自定义镜像的创建
文章目录 前言:项目部署的挑战一、初识 Docker1.1 什么是 Docker1.2 Docker 与 虚拟机的区别1.3 镜像和容器以及镜像托管平台1.4 Docker的架构解析1.5 Docker 在 CentOS 中的安装 二、Docker 的基本操作2.1 操作 Docker 镜像命令2.1.1 镜像操作相关命令2.1.2 示例一…...

【Docker】简易版harbor部署
文章目录 依赖于docker-compose下载添加执行权限测试 安装harbor下载解压修改配置文件部署配置开机自启动登录验证 使用harbor登录打标签上传下载 常见问题 依赖于docker-compose 下载 curl -L “https://github.com/docker/compose/releases/download/2.22.0/docker-compose-…...
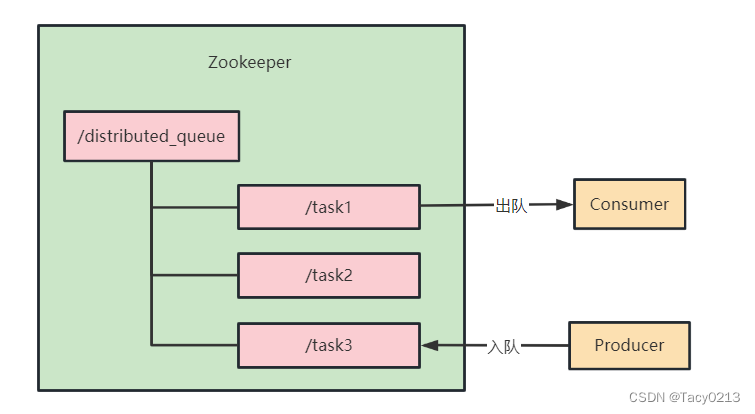
Zookeeper经典应用场景实战(一)
文章目录 1、Zookeeper Java客户端实战1.1、 Zookeeper 原生Java客户端使用1.2、 Curator开源客户端使用 2、 Zookeeper在分布式命名服务中的实战2.1、 分布式API目录2.2、 分布式节点的命名2.3、 分布式的ID生成器 3、Zookeeper实现分布式队列3.1、 设计思路3.2、 使用Apache …...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
