数据结构与算法(持续更新)
线性表
单链表
单链表的定义
由于顺序表的插入删除操作需要移动大量的元素,影响了运行效率,因此引入了线性表的链式存储——单链表。单链表通过一组任意的存储单元来存储线性表中的数据元素,不需要使用地址连续的存储单元,因此它不要求在逻辑上相邻的两个元素在物理位置上也相邻。
单链表的特点
1.单链表不要求逻辑上相邻的两个元素在物理位置上也相邻,因此不需要连续的存储空间。
2.单链表是非随机的存储结构,即不能直接找到表中某个特定的结点。查找某个特定的结点时,需要从表头开始遍历,依次查找。
**单链表操作**#include<iostream>
using namespace std;typedef struct LNode{int data;struct LNode *next;
}LNode,*LinkList;//初始化
void InitList(LinkList &L){L=(LNode *)malloc(sizeof(LinkList));L->next=NULL;
}//头插法建表
LinkList HeadInsert(LinkList &L){InitList(L);int x;while(cin>>x){LNode *s=(LNode *)malloc(sizeof(LNode));s->data=x;s->next=L->next;L->next=s;}return L;
}//尾插法建表
LinkList TailInsert(LinkList &L){InitList(L);LNode *s,*r=L;int x;while(cin>>x){s=(LNode *)malloc(sizeof(LNode));s->data=x;r->next=s;r=s;}r->next=NULL;return L;
} //输出表中元素
void PrintList(LinkList L){LNode *p=L->next;while(p!=NULL){cout<<p->data<<" ";p=p->next;}
} //求单链表的长度
int Length(LinkList L){LNode *p = L->next;int len = 0;while(p!=NULL){len++;p = p->next;}return len;
}//按值查找:查找x在L中的位置
LNode *LocateElem(LinkList L, int x){LNode *p = L->next;while(p!=NULL&&p->data!=x){p = p->next;}return p;
}//按位查找:查找在单链表L中第i个位置的结点
LNode *GetElem(LinkList L, int i){int j=1;LNode *p = L->next;if(i==0){return L;}if(i<1){return NULL;}while(p!=NULL&&j<i){p = p->next;j++;}return p;
}//判空操作
void Empty(LinkList L){if(L->next == NULL){cout<<"L is null"<<endl;}else{cout<<"L is not null"<<endl;}
}//将x插入到单链表L的第i个位置上
void Insert(LinkList &L, int i, int x){LNode *p = GetElem(L,i-1);LNode *s = (LNode *)malloc(sizeof(LNode));s->data = x;s->next = p->next;p->next = s;
}//删除操作:将单链表中的第i个结点删除
void Delete(LinkList &L, int i){if(i<0||i>Length(L)){cout<<"数据有误"; return ;}LNode *p = GetElem(L,i-1);LNode *q = p->next;p->next = q->next;free(q);
}int main(){**自定义补充**return 0;
}
双链表
循环链表
栈、队列、数组
树
图
查找
排序
排序算法可以分为内部排序和外部排序,其中内部排序有:插入排序(直接插入排序、折半插入排序、希尔排序)、交换排序(冒泡排序、快速排序)、选择排序(简单选择排序、堆排序)、归并排序、基数排序;外部排序有:多路归并排序。
插入排序
插入排序是一种简单直观的排序方法,其基本思想是每次将一个待排序的记录按其关键字大小插入前面已排好序的子序列,直到全部记录插入完成。由插入排序的思想可以引申出三个重要的排序算法:直接插入排序、折半插入排序和希尔排序。
直接插入排序
要将元素 L(i)插入已有序的子序列 L[1…i-1],需要执行以下操作(为避免混,下面用L[ ]表示一个表,而用 L( )表示一个元素):
1)查找出L(i)在L[l…i-1]中的插入位置k。
2)将L[k…i-1]中的所有元素依次后移一个位置。
3)将L(i)复制到L(k)。
#include<iostream>
using namespace std;void InsertSort(int a[],int len){int temp,i,j;for(i=1;i<len;i++){if(a[i]<a[i-1]){temp=a[i];for(j=i-1;temp<a[j];j--){a[j+1]=a[j]; }a[j+1]=temp;}}
} int main(){int a[]={1,3,4,2,6,5,9,8,7};int l=sizeof(a)/sizeof(int);InsertSort(a,l);for(int i=0;i<l;i++){cout<<a[i]<<" ";} return 0;
}
时间复杂度:O(n^2) 最好情况下:O(n)
空间复杂度:O(1)
稳定性:由于每次插入元素时总是从后向前先比较再移动,所以不会出现相同元素相对位置发生变化的情况,即直接插入排序是一个稳定的排序方法。
适用性:直接插入排序算法适用于顺序存储和链式存储的线性表。为链式存储时,可以从前往后查找指定元素的位置。
折半插入排序
从直接插入排序算法中,不难看出每趟插入的过程中都进行了两项工作:1.从前面的有序子表中查找出待插入元素应该被插入的位置;2.给插入位置腾出空间,将待插入元素复制到表中的插入位置。注意到在该算法中,总是边比较边移动元素。下面将比较和移动操作分离,即先折半查找出元素的待插入位置,然后统一地移动待插入位置之后的所有元素。当排序表为顺序表时,可以对直接插入排序算法做如下改进:由于是顺序存储的线性表,所以查找有序子表时可以用折半查找来实现。确定待插入位置后,就可统一地向后移动元素。
#include<iostream>
using namespace std;void InsertSort(int a[],int len){int temp,low,high,mid;for(int i=1;i<len;i++){temp=a[i];low=0,high=i-1;while(low<=high){mid=(low+high)/2;if(a[mid]>temp){high=mid-1;}else{low=mid+1;}}for(int j=i-1;j>=high+1;j--){a[j+1]=a[j];}a[high+1]=temp;}
}int main(){int a[]={1,3,4,2,6,5,9,8,7};int l=sizeof(a)/sizeof(int);InsertSort(a,l);for(int i=0;i<l;i++){cout<<a[i]<<" ";}return 0;
}
从上述算法中,不难看出折半插入排序仅减少了比较元素的次数,约为 O(nlogn),该比较次数与待排序表的初始状态无关,仅取决于表中的元素个数n;而元素的移动次数并未改变,它依赖于待排序表的初始状态。因此,折半插入排序的时间复杂度仍为 O(n^2),但对于数据量不很大的排序表,折半插入排序往往能表现出很好的性能。折半插入排序是一种稳定的排序方法。
希尔排序
希尔排序的基本思想是:先将待排序表分割成若干形如L[i,i+d,i+2d,i+3d,…,i+kd]的“特殊”子表,即把相隔某个“增量”的记录组成一个子表,对各个子表分别进行直接插入排序,当整个表中的元素已呈“基本有序”时,再对全体记录进行一次直接插入排序。
希尔排序的过程如下:先取一个小于n 的步长 d1,把表中的全部记录分成d1组,所有距离为d1的倍数的记录放在同一组,在各组内进行直接插入排序;然后取第二个步长 d2<d1,重复上述过程,直到所取到的di=1,即所有记录已放在同一组中,再进行直接插入排序,由于此时已经具有较好的局部有序性,故可以很快得到最终结果。
#include<iostream>
using namespace std;void InsertSort(int a[],int len){for(int d=len/2;d>=1;d=d/2){int temp,i,j;for(i=d+1;i<len;i++){if(a[i]<a[i-d]){temp=a[i];for(j=i-d;j>0&&temp<a[j];j-=d){a[j+d]=a[j]; }a[j+d]=temp;}}}
} int main(){int a[]={1,3,4,2,6,5,9,8,7};int l=sizeof(a)/sizeof(int); InsertSort(a,l);for(int i=0;i<l;i++){cout<<a[i]<<" ";}return 0;
}
空间效率:仅使用了常数个辅助单元,因而空间复杂度为 O(1)。
时间效率:由于希尔排序的时间复杂度依赖于增量序列的函数,这涉及数学上尚未解决的难题,所以其时间复杂度分析比较困难。当n在某个特定范围时,希尔排序的时间复杂度约为O(n^1.3)。在最坏情况下希尔排序的时间复杂度为 O(n^2)。
稳定性:当相同关键字的记录被划分到不同的子表时,可能会改变它之间的相对次序,因此希尔排序是一种不稳定的排序方法。
适用性:希尔排序算法仅适用于线性表为顺序存储的情况。
交换排序
所谓交换,是指根据序列中两个元素关键字的比较结果来对换这两个记录在序列中的位置。基于交换的排序算法很多,主要有冒泡排序和快速排序。
冒泡排序
冒泡排序的基本思想是:从后往前(或从前往后)两两比较相邻元素的值,若为逆序(即A[i-1]>A[i]),则交换它们,直到序列比较完。我们称它为第一趟冒泡,结果是将最小的元素交换到待排序列的第一个位置(或将最大的元素交换到待排序列的最后一个位置),关键字最小的元素如气泡一般逐渐往上“漂浮”直至“水面”(或关键字最大的元素如石头一般下沉至水底)。下一趟冒泡时,前一趟确定的最小元素不再参与比较,每趟冒泡的结果是把序列中的最小元素(或最大元素)放到了序列的最终位置…这样最多做n-1趟冒泡就能把所有元素排好序。
#include<iostream>
using namespace std;void BubbleSort(int a[],int len){for(int i=0;i<len-1;i++){for(int j=0;j<len-i;j++){if(a[j+1]<a[j]){swap(a[j+1],a[j]);}}}
} int main(){int a[]={1,3,4,2,6,5,9,8,7};int l=sizeof(a)/sizeof(int); BubbleSort(a,l);for(int i=0;i<l;i++){cout<<a[i]<<" ";}return 0;
}
算法改进:由上述的示例(数组元素为:1,3,4,2,6,5,9,8,7)可知,其第二趟的结果(1,2,3,4,5,6,7,8,9)已经有序,后面再进行排序其实是重复动作。因此,当某一趟的结果已经有序时,表示所给序列已经有序,不必要再进行下一趟排序。
void BubbleSort(int a[],int len){for(int i=0;i<len-1;i++){bool flag=false; for(int j=0;j<len-i;j++){if(a[j+1]<a[j]){swap(a[j+1],a[j]);flag=true;}}if(flag==false){return ;}}
}
空间效率:仅使用了常数个辅助单元,因而空间复杂度为 O(1)。
时间效率:当初始序列有序时,显然第一趟冒泡后flag依然为false(本趟冒泡没有元素交换),从而直接跳出循环,比较次数为n-1,移动次数为0,从而最好情况下的时间复杂度为O(n);当初始序列为逆序时,需要进行n-1趟排序,第i趟排序要进行n-i次关键字的比较,而且每次比较后都必须移动元素3次来交换元素位置。这种情况下的时间复杂度为 O(n^2),其平均时间复杂度也为 O(n^2)。
稳定性:由于i>j且a[i]=a[j]时,不会发生交换,因此冒泡排序是一种稳定的排序方法。
快速排序
快速排序的基本思想是基于分治法的:在待排序表 L[l…n]中任取一个元素pivot作为枢轴(或基准,通常取首元素),通过一趟排序将待排序表划分为独立的两部分L[1…k-1]和L[k+l…n],使得L[l…k-1]中的所有元素小于pivot,L[k+l…n]中的所有元素大于等于pivot,则pivot放在了其最终位置 L(k)上,这个过程称为一趟快速排序(或一次划分)。然后分别递归地对两个子表重复上述过程,直至每部分内只有一个元素或空为止,即所有元素放在了其最终位置上。
#include<iostream>
using namespace std;void QuickSort(int a[],int low,int high){int i=low,j=high,pivot=a[low];if(low>=high){return ;}while(i<j){while(a[j]>=pivot&&i<j){j--;}a[i]=a[j];while(a[i]<=pivot&&i<j){i++;}a[j]=a[i];}a[i]=pivot;QuickSort(a,low,i-1);QuickSort(a,i+1,high);
}int main(){int a[]={1,3,4,2,6,5,9,8,7};int l=sizeof(a)/sizeof(int); QuickSort(a,0,l-1);for(int i=0;i<l;i++){cout<<a[i]<<" ";}return 0;
}
**快速排序另一种写法:**int Partition(int a[],int low,int high){int pivot=a[low];while(low<high){while(a[high]>pivot&&low<high){high--;}a[low]=a[high];while(a[low]<pivot&&low<high){low++;}a[high]=a[low];}a[low]=pivot;return low;
}void QuickSort(int a[],int low,int high){if(low<high){int pivotpos = Partition(a,low,high);QuickSort(a,low,pivotpos-1);QuickSort(a,pivotpos+1,high);}
}
选择排序
选择排序的基本思想是:每一趟(如第i趟)在后面n-i+1(i=1,2,…,n-1)个待排序元素中选取关键字最小的元素,作为有序子序列的第i个元素,直到第n-1趟做完,待排序元素只剩下1个,就不用再选了。选择排序主要有简单选择排序和堆排序。
简单选择排序
简单选择排序算法的思想:假设排序表为L[1…n],第i趟排序即从L[i…n]中选择关键字最小的元素与L(i)交换,每一趟排序可以确定一个元素的最终位置,这样经过n-1趟排序就可使得整个排序表有序。
#include<iostream>
using namespace std;void SelectSort(int a[],int len){for(int i=0;i<len-1;i++){int min=i;for(int j=i+1;j<len;j++){if(a[j]<a[min]){min=j;}}if(min!=i){swap(a[i],a[min]);}}
} int main(){int a[]={1,3,4,2,6,5,9,8,7};int l=sizeof(a)/sizeof(int); SelectSort(a,l);for(int i=0;i<l;i++){cout<<a[i]<<" ";}return 0;
}
空间效率:仅使用常数个辅助单元,故空间效率为0(1)。
时间效率:从上述代码中不难看出,在简单选择排序过程中,元素移动的操作次数很少,不会超过3(n-1)次,最好的情况是移动0次,此时对应的表已经有序,但元素间比较的次数与序列的初始状态无关,始终是 n(n-1)/2 次,因此时间复杂度始终是 O(n^2)。
稳定性:在第i趟找到最小元素后,和第 i个元素交换,可能会导致第i个元素与其含有相同关键字元素的相对位置发生改变。例如,表L={2,2,1},经过一趟排序后L={1,2,2},最终排序序列也是L={1,2,2},显然,2与2的相对次序已发生变化。因此,简单选择排序是一种不稳定的排序方法。
堆排序
堆的定义如下,n个关键字序列L[1…n]称为堆,当且仅当该序列满足:
1.L(i)>=L(2i)且L(i)>=L(2i+1)或
2.L(i)<=L(2i)且L(i)<=(2i+1) (1 <= i <= n/2)
堆排序的思路很简单:首先将存放在L[1…n]中的n个元素建成初始堆,由于堆本身的特点(以大顶堆为例),堆顶元素就是最大值。输出堆顶元素后,通常将堆底元素送入堆顶,此时根结点已不满足大顶堆的性质,堆被破坏,将堆顶元素向下调整使其继续保持大顶堆的性质,再输出堆顶元素。如此重复,直到堆中仅剩一个元素为止。可见堆排序需要解决两个问题:1.如何将无序序列构造成初始堆?2.输出堆顶元素后,如何将剩余元素调整成新的堆?
堆排序的关键是构造初始堆。n个结点的完全二叉树,最后一个结点是第n/2个结点的孩子。对第n/2个结点为根的子树筛选(对于大根堆,若根结点的关键字小于左右孩子中关键字较大者,则交换),使该子树成为堆。之后向前依次对各结点(n/2-1,…,1)为根的子树进行筛选,看该结点值是否大于其左右子结点的值,若不大于,则将左右子结点中的较大值与之交换,交换后可能会破坏下一级的堆,于是继续采用上述方法构造下一级的堆,直到以该结点为根的子树构成堆为止。反复利用上述调整堆的方法建堆,直到根结点。
#include<iostream>
using namespace std;void HeapAdjust(int a[],int k,int len){a[0]=a[k];for(int i=2*k;i<=len;i*=2){if(i<len&&a[i]<a[i+1]){i++; }if(a[0]>=a[i]){break;}else{a[k]=a[i];k=i;}}a[k]=a[0];
}void BuildMaxHeap(int a[],int len){for(int i=len/2;i>0;i--){HeapAdjust(a,i,len);}
}void HeapSort(int a[],int len){BuildMaxHeap(a,len);for(int i=len;i>1;i--){swap(a[i],a[1]);HeapAdjust(a,1,i-1);}
} int main(){int b[]={1,3,4,2,6,5,9,8,7};int a[100],l=sizeof(b)/sizeof(int);for(int i=0;i<l;i++){a[i+1]=b[i];}HeapSort(a,l);for(int i=1;i<=l;i++){cout<<a[i]<<" ";}return 0;
}
空间效率:仅使用了常数个辅助单元,所以空间复杂度为 O(1)。
时间效率:建堆时间为 O(n),之后有 n-1次向下调整操作,每次调整的时间复杂度为 O(h),故在最好、最坏和平均情况下,堆排序的时间复杂度为O(nlogn)。
稳定性:进行筛选时,有可能把后面相同关键字的元素调整到前面,所以堆排序算法是一种不稳定的排序方法。例如,表L={1,2,2},构造初始堆时可能将2交换到堆顶,此时L={2,1,2},最终排序序列为 L={1,2,2},显然,2与2的相对次序已发生变化。
归并排序
归并排序是比较稳定的排序方法。它的基本思想是把待排序的元素分解成两个规模大致相等的子序列。如果不易分解,将得到的子序列继续分解,直到子序列中包含的元素个数为1。因为单个元素的序列本身就是有序的,此时便可以进行合并,从而得到一个完整的有序序列。
分治算法
归并排序,其实就是一种分治算法,那么在了解归并排序之前,我们先来看看什么是分治算法。在算法设计中,我们引入分而治之的策略,称为分治算法,其本质就是将一个大规模的问题分解为若干个规模较小的相同子问题,分而治之。
分治算法解题
1.分解:将要解决的问题分解为若干个规模较小、相互独立、与原问题形式相同的子问题。
2.治理:求解各个子问题。由于各个子问题与原问题形式相同,只是规模较小而已,而当子问题划分得足够小时,就可以用简单的方法解决。
3.合并:按原问题的要求,将子问题的解逐层合并构成原问题的解。
归并排序解题步骤
步骤一:首先将待排序的元素分成大小大致相同的两个序列。
步骤二:再把子序列分成大小大致相同的两个子序列。
步骤三:如此下去,直到分解成一个元素停止,这时含有一个元素的子序列都是有序的。
步骤四:进行合并操作,将两个有序的子序列合并为一个有序序列,如此下去,直到所有的元素都合并为一个有序序列。
数据模拟,下面我将以序列(4,9,15,24,30,2,6,18,20)进行图解
1、初始化:i = low,j = mid+1,mid = (low+high)/2 ,申请一个辅助数组 b

int b[high-low+1];
int i = low, j = mid + 1, k = 0;
2、现在比较 a[i] 和 b[j],将较小的元素放在 b 数组中,相应的指针向后移动,直到 i > mid 或者 j>hight 时结束。
while (i <= mid && j <= high) {if (a[i] <= a[j]) {b[k++] = a[i++]; } else {b[k++] = a[j++];}
}
进行第一次比较 a[i]=4 和 a[j]=2,将较小的元素 2 放入数组 b 中,j++,k++,如下图:

进行第二次比较 a[i]=4 和 a[j]=6,将较小的元素放 4 入数组 b 中,i++,k++,如下图:

进行第三次比较 a[i]=9 和 a[j]=6,将较小的元素放 6 入数组 b 中,j++,k++,如下图:

进行第四次比较 a[i]=9 和 a[j]=18,将较小的元素放 9 入数组 b 中,i++,k++,如下图:

进行第五次比较 a[i]=15 和 a[j]=18,将较小的元素放 15 入数组 b 中,i++,k++,如下图:

进行第六次比较 a[i]=24 和 a[j]=18,将较小的元素放 18 入数组 b 中,j++,k++,如下图:

进行第七次比较 a[i]=24 和 a[j]=20,将较小的元素放 20 入数组 b 中,j++,k++,如下图:

此时,j>hight 了,while循环结束,但 a 数组还剩下元素(i<mid)可直接放入 b 数组就可以了。如下图所示:

while (i <= mid){ // j 序列结束,将剩余的 i 序列补充在 b 数组中 b[k++] = a[i++];
}
while (j <= high){ // i 序列结束,将剩余的 j 序列补充在 b 数组中 b[k++] = a[j++];
}
现在比较 a[i] 和 b[j] ,将较小的元素放在 b 数组中,相应的指针向后移动,直到 i > mid 或者 j > hight 时结束。
while (i <= mid && j <= high) {if (a[i] <= a[j]) {b[k++] = a[i++]; } else {b[k++] = a[j++];}
}
现在将 b 数组的元素赋值给 a 数组,再将 b 数组销毁,即可。
for (int i = low; i <= hight; i++) { //将 b 数组的值传递给数组 aa[i] = b[k++];
}
delete[]b; // 辅助数组用完后,将其的空间进行释放(销毁)
3、递归的形式进行归并排序
void MergeSort(int a[ ],int low,int high){if(low<high){int mid=(low+high)/2;MergeSort(a,low,mid);MergeSort(a,mid+1,high);Merge(a,low,mid,high);}
}
**完整代码**
#include<iostream>
using namespace std;void Merge(int a[],int low,int mid,int high){int *b=new int[high-low+1]; //用 new 申请一个辅助函数int i = low, j = mid + 1, k = 0; // k为 b 数组的小标while (i <= mid && j <= high){if (a[i] <= a[j]){b[k++] = a[i++]; //按从小到大存放在 b 数组里面}else{b[k++] = a[j++];}}while (i <= mid){ // j 序列结束,将剩余的 i 序列补充在 b 数组中 b[k++] = a[i++];}while (j <= high){ // i 序列结束,将剩余的 j 序列补充在 b 数组中 b[k++] = a[j++];}k = 0; //从小标为 0 开始传送for (int i = low; i <= high; i++){ //将 b 数组的值传递给数组 aa[i] = b[k++];}delete []b; //销毁
}void MergeSort(int a[],int low,int high){if(low<high){int mid=(low+high)/2;MergeSort(a,low,mid);MergeSort(a,mid+1,high);Merge(a,low,mid,high);}
}int main(){int a[]={1,3,4,2,6,5,9,8,7};int l=sizeof(a)/sizeof(int);MergeSort(a,0,l-1);for(int i=0;i<l;i++){cout<<a[i]<<" ";}return 0;
}
基数排序
相关文章:

数据结构与算法(持续更新)
线性表 单链表 单链表的定义 由于顺序表的插入删除操作需要移动大量的元素,影响了运行效率,因此引入了线性表的链式存储——单链表。单链表通过一组任意的存储单元来存储线性表中的数据元素,不需要使用地址连续的存储单元,因此它…...
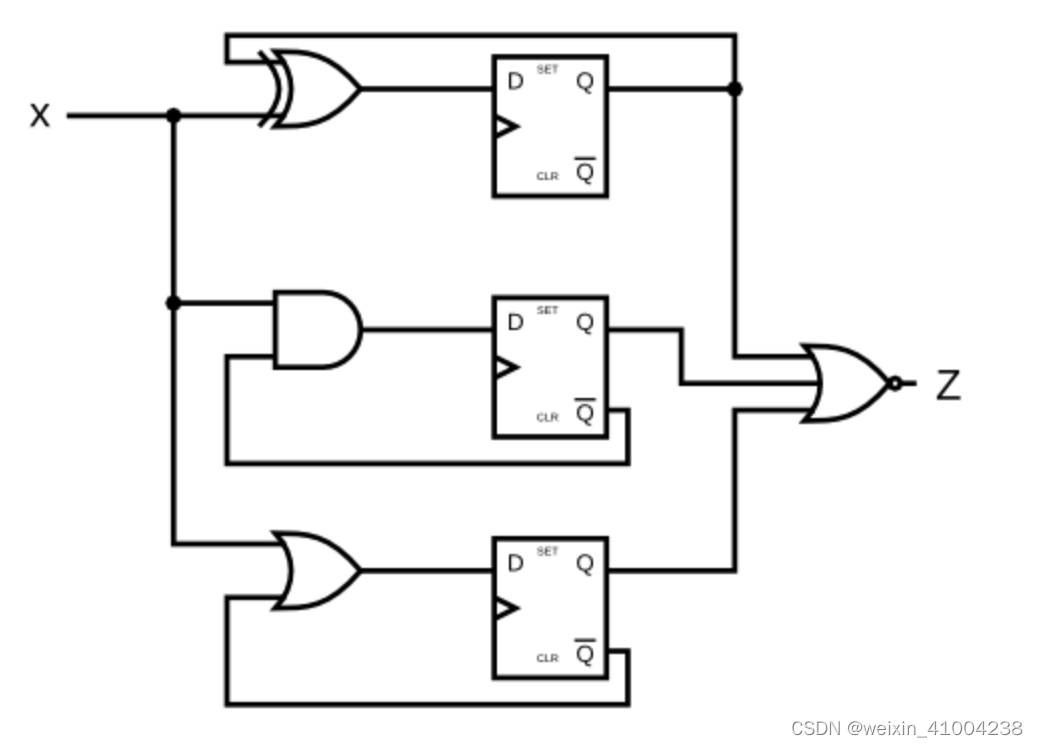
HDLbits: ece241 2014 q4
module top_module (input clk,input x,output z ); reg [2:0] Q;always(posedge clk)beginQ[0] < Q[0] ^ x;Q[1] < (~Q[1]) & x;Q[2] < (~Q[2]) | x;z < ~(| Q[2:0]); //错误!!!!endendmodule 正确答案…...
-- gmssl - 国密算法)
LuatOS-SOC接口文档(air780E)-- gmssl - 国密算法
sm.sm2encrypt(pkx,pky,data)# sm2算法加密 参数 传入值类型 解释 string 公钥x,必选 string 公钥y,必选 string 待计算的数据,必选,最长255字节 返回值 返回值类型 解释 string 加密后的字符串, 原样输出,未经HEX转换 例子 local originStr "encryptio…...

【线性代数及其应用 —— 第一章 线性代数中的线性方程组】-1.线性方程组
所有笔记请看: 博客学习目录_Howe_xixi的博客-CSDN博客https://blog.csdn.net/weixin_44362628/article/details/126020573?spm1001.2014.3001.5502思维导图如下: 内容笔记如下:...
vue实现拖拽排序
在业务中列表拖拽排序是比较常见的需求,常见的JS拖拽库有Sortable.js,Vue.Draggable等,大多数同学遇到这种需求也是更多的求助于这些JS库,其实,使用HTML原生的拖放事件来实现拖拽排序并不复杂,结合Vue的tra…...
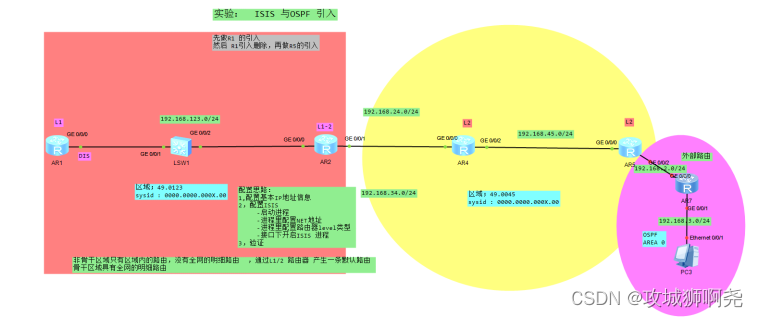
IS-IS
二、IS-IS中的DIS与OSPF中的DR Level-1和Level-2的DIS是分别选举的,用户可以为不同级别的DIS选举设置不同的优先级。DIS的选举规则如下:DIS优先级数值最大的被选为DIS。如果优先级数值最大的路由器有多台,则其中MAC地址最大的路由器会成为DI…...
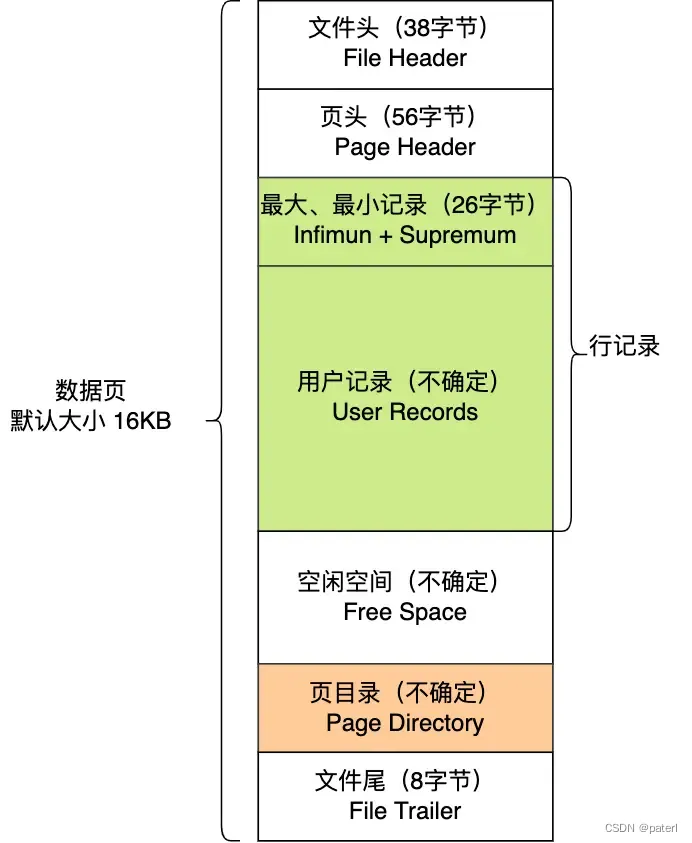
【MySQL】为什么使用B+树做索引
MySQL的innoDB引擎使用的是B树的结构来存储索引的,那么为什么会使用B树呢?为什么不使用其他的结构?本篇我们深入MySQL底层来了解B树。本文中说到的MySQL都是InnoDB引擎的 在这之前,先了解一下InnoDB是如何存储数据的 MySQL是根据数据页的方式…...
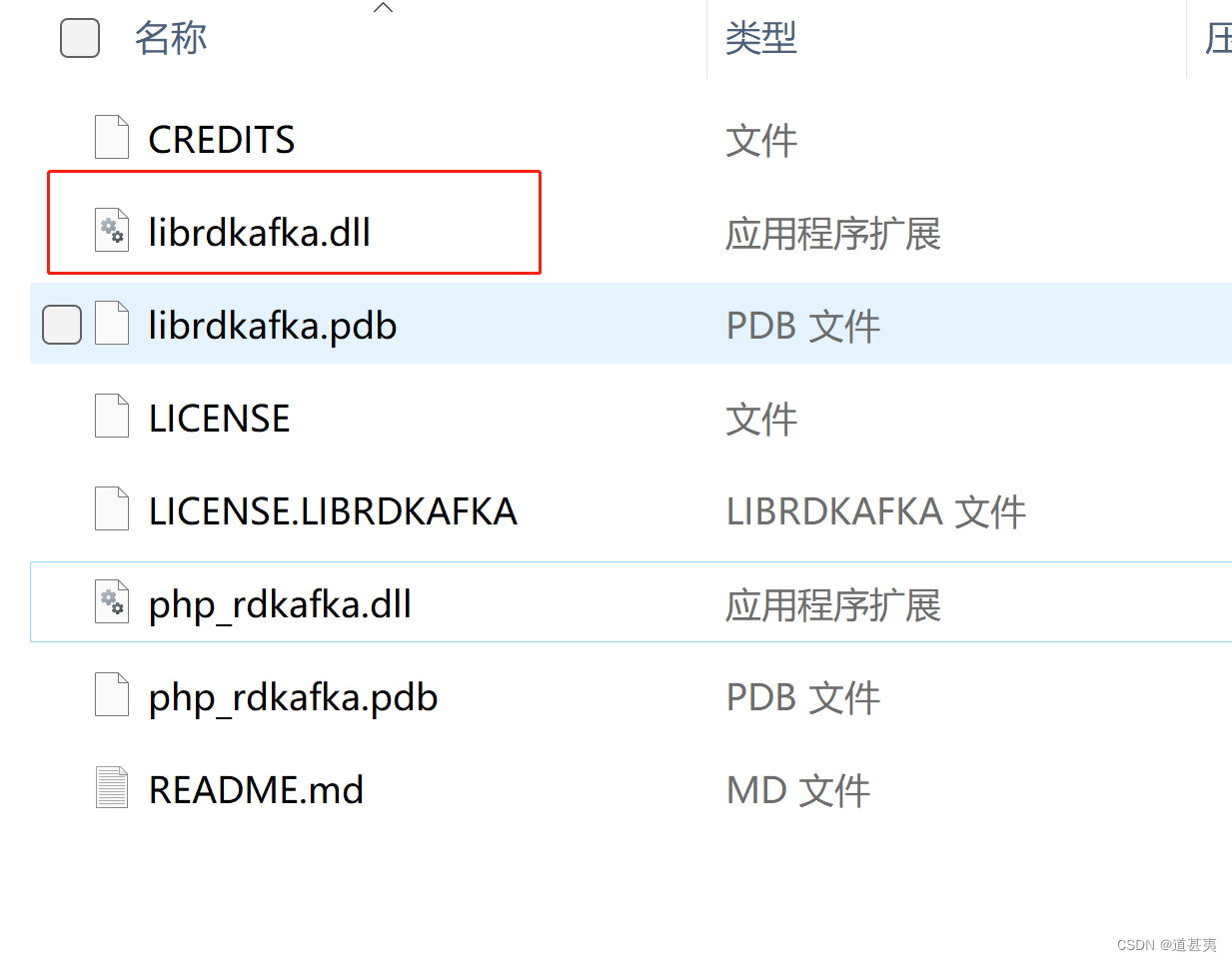
php 安装mongodb扩展模块,rdkafka模块
mongodb mongodb扩展下载 选择php版本,根据报错提示,选择扩展对应的版本选择非安全进程将php_mongodb.dll放到php/ext目录下修改php.ini配置,添加extensionphp_mongodb.dll开启php_mongodb扩展,重启服务php -m 查看是否开启成功…...

【数据结构】初探时间与空间复杂度:算法评估与优化的基础
🚩纸上得来终觉浅, 绝知此事要躬行。 🌟主页:June-Frost 🚀专栏:数据结构 🔥该文章主要了解算法的时间复杂度与空间复杂度等相关知识。 目录: 🌏 时间复杂度🔭…...

SpringCloud Alibaba - Sentinel 限流规则(案例 + JMeter 测试分析)
目录 一、Sentinel 限流规则 1.1、簇点链路 1.2、流控模式 1.2.1、直接流控模式 1.2.2、关联流控模式 a)在 OrderController 中新建两个端点. b)在 Sentinel 控制台中对订单查询端点进行流控 c)使用 JMeter 进行测试 d)分…...

uniapp 条件编译 APP 、 H5 、 小程序
一、#ifdef、#ifndef、 #endif三者的区别、 标识作用#ifdef仅在某个平台上使用#ifndef在除了这个平台的其他平台上使用(非此平台使用)#endif结束条件编译 二、平台标识 标识平台APP-PLUS5AppMP微信小程序/支付宝小程序/百度小程序/头条小程序/QQ小程序MP-WEIXIN微…...
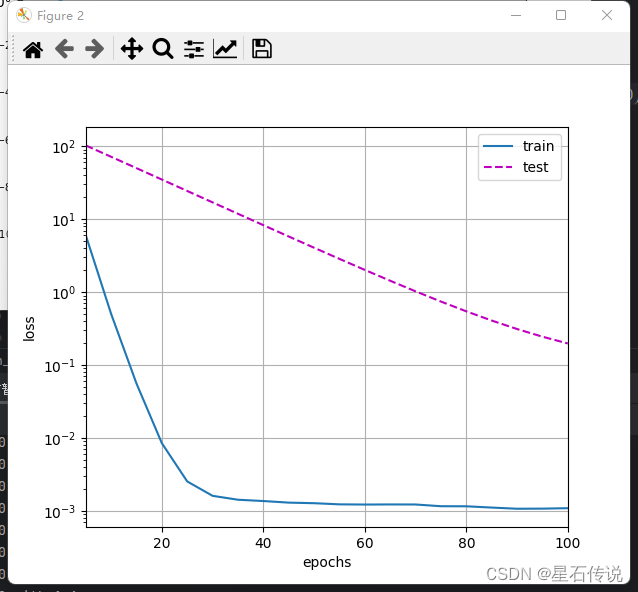
深度学习——权重衰减(weight_decay)
深度学习——权重衰减(weight_decay) 文章目录 前言一、权重衰减1.1. 范数与权重衰减1.2. 高维线性回归1.3. 从零开始实现1.3.1.初始化模型参数1.3.2. 定义L₂范数惩罚1.3.3. 定义训练代码实现1.3.4. 不管正则化直接训练1.3.5. 使用权重衰减 1.4. 简洁实现 总结 前言…...

nignx如何部署让前端不用清缓存就可以部署
在Nginx中,可以使用以下方法来部署前端应用程序,使前端用户无需清空缓存即可进行部署: 1、使用版本号:在前端应用程序的构建过程中,可以添加一个独特的版本号到应用程序的名称中。每次部署时,将版本号更新…...

CSS3实现动画加载效果
<!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>加载效果</title><link rel"style…...

springboot定时任务Scheduled使用和弊端分析
1.springboot定时任务Scheduled使用说明: (1)创建定时任务类 import com.one.utils.DateUtil; import org.springframework.beans.factory.annotation.Autowired; import...

openGauss学习笔记-93 openGauss 数据库管理-访问外部数据库-oracle_fdw
文章目录 openGauss学习笔记-93 openGauss 数据库管理-访问外部数据库-oracle_fdw93.1 编译oracle_fdw93.2 使用oracle_fdw93.3 常见问题93.4 注意事项 openGauss学习笔记-93 openGauss 数据库管理-访问外部数据库-oracle_fdw openGauss的fdw实现的功能是各个openGauss数据库及…...

【Git】Git下载安装环境配置 下载速度慢的解决方案
这里写自定义目录标题 介绍一、下载官网下载镜像站 二、安装安装成功 三、Git三种界面介绍Git cmd界面展示git bash界面展示git GUI界面展示 四、环境配置配置流程1、打开环境变量界面2、添加环境变量 /删除环境变量3、在变量中找到Git\cmd的值就表示配置成功4、没有找到点击新…...

常见源协议介绍
开源协议(Open Source License)是一种法律文档,用于规定如何使用、修改和分发开源软件和其他开源项目的规则和条件。这些协议允许创作者或组织将其创造的代码或作品以开放源代码的形式共享给他人,以促进协作、创新和知识共享。常见…...
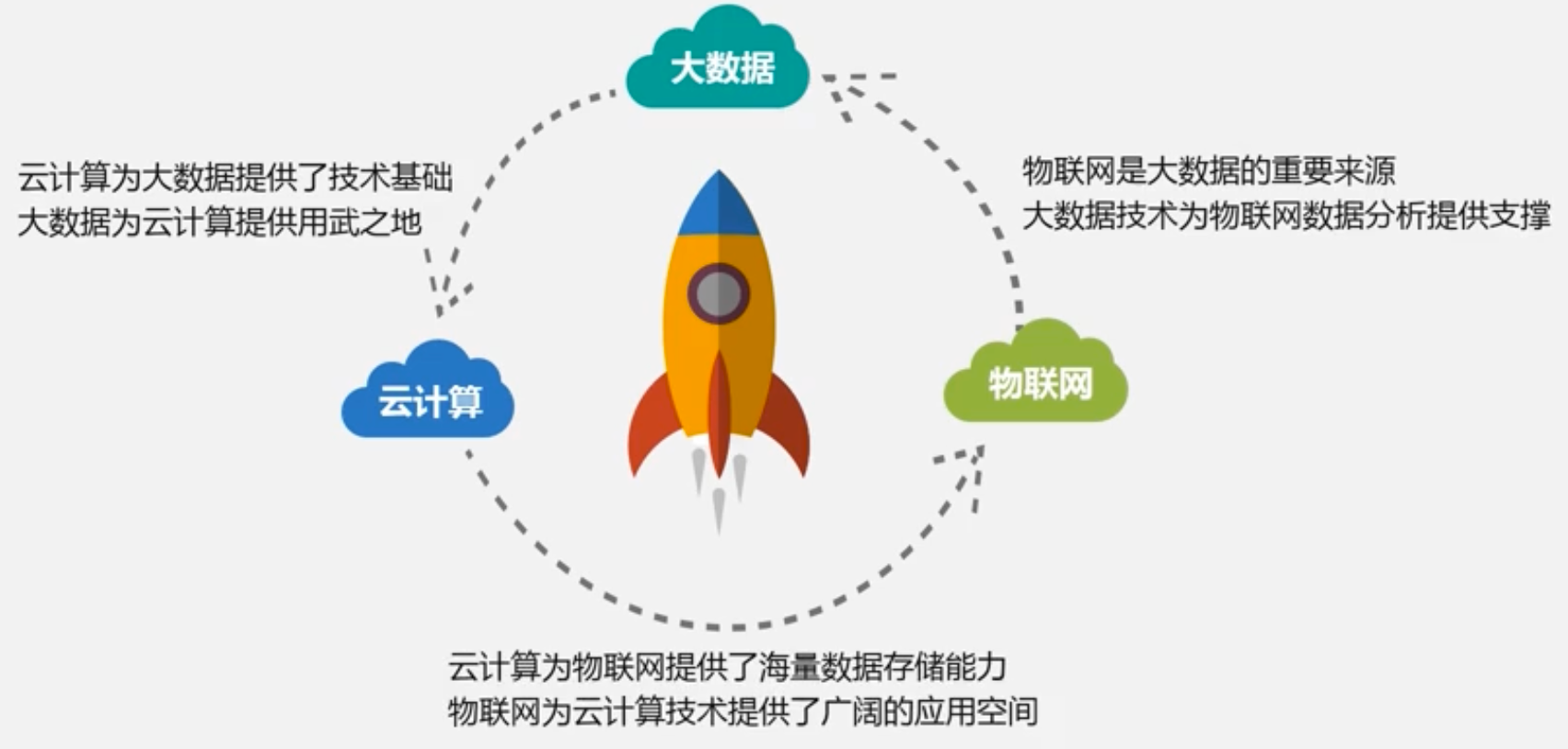
大数据概述(林子雨慕课课程)
文章目录 1. 大数据概述1.1 大数据概念和影响1.2 大数据的应用1.3 大数据的关键技术1.4 大数据与云计算和物联网的关系云计算物联网 1. 大数据概述 大数据的四大特点:大量化、快速化、多样化、价值密度低 1.1 大数据概念和影响 大数据摩尔定律 大数据由结构化和非…...
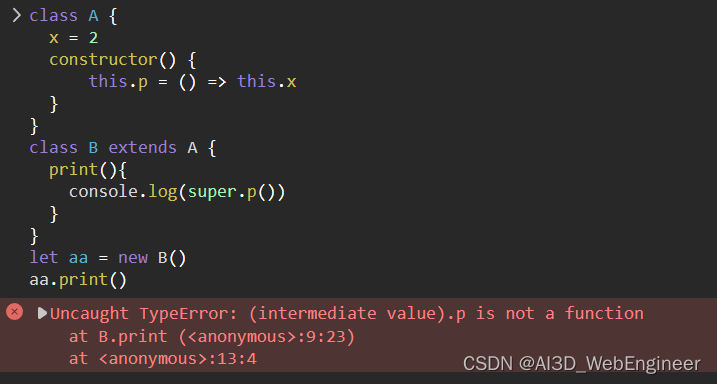
ES6 class类关键字super
super关键字 在 JavaSCript 中,能通过 extends 关键字去继承父类 super 关键字在子类中有以下用法: 当成函数调用 super() 作为 "属性查询" super.prop 和 super[expr] super() super 作为函数调用时,代表父类的构造函数。 ES6 要求…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
