深度学习——权重衰减(weight_decay)
深度学习——权重衰减(weight_decay)
文章目录
- 前言
- 一、权重衰减
- 1.1. 范数与权重衰减
- 1.2. 高维线性回归
- 1.3. 从零开始实现
- 1.3.1.初始化模型参数
- 1.3.2. 定义L₂范数惩罚
- 1.3.3. 定义训练代码实现
- 1.3.4. 不管正则化直接训练
- 1.3.5. 使用权重衰减
- 1.4. 简洁实现
- 总结
前言
上一章描述了过拟合的问题,本章我们将介绍一些正则化模型的技术。如权重衰减
参考书:
《动手学深度学习》
一、权重衰减
1.1. 范数与权重衰减
在训练参数化机器学习模型时,权重衰减(weight decay)是最广泛使用的正则化的技术之一, 它通常也被称为 L 2 L_2 L2正则化。这项技术通过函数与零的距离来衡量函数的复杂度,
因为在所有函数 f f f中,函数 f = 0 f = 0 f=0(所有输入都得到值 0 0 0),在某种意义上是最简单的。
但是我们应该如何精确地测量一个函数和零之间的距离呢?
一种简单的方法是通过线性函数
f ( x ) = w ⊤ x f(\mathbf{x}) = \mathbf{w}^\top \mathbf{x} f(x)=w⊤x 中的权重向量的某个范数来度量其复杂性,
例如 ∥ w ∥ 2 \| \mathbf{w} \|^2 ∥w∥2。
要保证权重向量比较小,最常用方法是将其范数作为惩罚项加到最小化损失的问题中:
即将原来的训练目标最小化训练标签上的预测损失,调整为最小化预测损失和惩罚项之和。
现在,如果我们的权重向量增长的太大,我们的学习算法可能会更集中于最小化权重范数 ∥ w ∥ 2 \| \mathbf{w} \|^2 ∥w∥2。这正是我们想要的。
我们的损失由下式给出:
L ( w , b ) = 1 n ∑ i = 1 n 1 2 ( w ⊤ x ( i ) + b − y ( i ) ) 2 . L(\mathbf{w}, b) = \frac{1}{n}\sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2. L(w,b)=n1i=1∑n21(w⊤x(i)+b−y(i))2.
为了惩罚权重向量的大小,我们必须以某种方式在损失函数中添加 ∥ w ∥ 2 \| \mathbf{w} \|^2 ∥w∥2
但是模型应该如何平衡这个新的额外惩罚的损失?
实际上,我们通过正则化常数 λ \lambda λ来描述这种权衡,这是一个非负超参数,我们使用验证数据拟合:
L ( w , b ) + λ 2 ∥ w ∥ 2 , L(\mathbf{w}, b) + \frac{\lambda}{2} \|\mathbf{w}\|^2, L(w,b)+2λ∥w∥2,
对于 λ > 0 \lambda > 0 λ>0,我们限制 ∥ w ∥ \| \mathbf{w} \| ∥w∥的大小。
为什么在这里我们使用平方范数而不是标准范数(即欧几里得距离)?
我们这样做是为了便于计算。通过平方 L 2 L_2 L2范数,我们去掉平方根,留下权重向量每个分量的平方和。
这使得惩罚的导数很容易计算:导数的和等于和的导数。
此外,为什么我们首先使用 L 2 L_2 L2范数,而不是 L 1 L_1 L1范数。
L 2 L_2 L2正则化线性模型构成经典的岭回归(ridge regression)算法,
L 1 L_1 L1正则化线性回归是统计学中类似的基本模型,通常被称为套索回归(lasso regression)。
使用 L 2 L_2 L2范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。在实践中,这可能使它们对单个变量中的观测误差更为稳定。
相比之下, L 1 L_1 L1惩罚会导致模型将权重集中在一小部分特征上,
而将其他权重清除为零。这称为特征选择(feature selection),可能是其他场景下需要的。
L 2 L_2 L2正则化回归的小批量随机梯度下降更新如下式:
w ← ( 1 − η λ ) w − η ∣ B ∣ ∑ i ∈ B x ( i ) ( w ⊤ x ( i ) + b − y ( i ) ) . \begin{aligned} \mathbf{w} & \leftarrow \left(1- \eta\lambda \right) \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right). \end{aligned} w←(1−ηλ)w−∣B∣ηi∈B∑x(i)(w⊤x(i)+b−y(i)).
我们根据估计值与观测值之间的差异来更新 w \mathbf{w} w。然而,我们同时也在试图将 w \mathbf{w} w的大小缩小到零。
这就是为什么这种方法有时被称为权重衰减。我们仅考虑惩罚项,优化算法在训练的每一步衰减权重。
与特征选择相比,权重衰减为我们提供了一种连续的机制来调整函数的复杂度。 较小的 λ \lambda λ值对应较少约束的 w \mathbf{w} w,而较大的 λ \lambda λ值对 w \mathbf{w} w的约束更大。
是否对相应的偏置 b 2 b^2 b2进行惩罚在不同的实践中会有所不同,
在神经网络的不同层中也会有所不同。通常,网络输出层的偏置项不会被正则化。
1.2. 高维线性回归
我们通过一个简单的例子来演示权重衰减。
首先,我们像以前一样生成一些数据,生成公式如下:
y = 0.05 + ∑ i = 1 d 0.01 x i + ϵ where ϵ ∼ N ( 0 , 0.0 1 2 ) . y = 0.05 + \sum_{i = 1}^d 0.01 x_i + \epsilon \text{ where } \epsilon \sim \mathcal{N}(0, 0.01^2). y=0.05+i=1∑d0.01xi+ϵ where ϵ∼N(0,0.012).
我们选择标签是关于输入的线性函数。标签同时被均值为0,标准差为0.01高斯噪声破坏。
为了使过拟合的效果更加明显,我们可以将问题的维数增加到 d = 200 d = 200 d=200,
并使用一个只包含20个样本的小训练集。
import torch
from d2l import torch as d2l
from torch import nnn_train,n_test,num_inputs,batch_size = 20,100,200,5
true_w,true_b = torch.ones((num_inputs,1))*0.01,0.05"""
使用d2l.synthetic_data函数生成了训练数据和测试数据,并使用d2l.load_array函数将数据加载为迭代器。
"""
train_data = d2l.synthetic_data(true_w,true_b,n_train)
train_iter = d2l.load_array(train_data,batch_size)test_data = d2l.synthetic_data(true_w,true_b,n_test)
test_iter = d2l.load_array(test_data,batch_size,is_train= False)
#这里设置is_train=False表示测试数据不用于模型训练,只用于评估模型的性能。1.3. 从零开始实现
下面我们将从头开始实现权重衰减,只需将 L 2 L_2 L2的平方惩罚添加到原始目标函数中。
1.3.1.初始化模型参数
#初始化模型参数
#我们将定义一个函数来随机初始化模型参数
def init_params():w = torch.normal(0,1,size=(num_inputs,1),requires_grad= True)b = torch.zeros(1,requires_grad=True)return [w,b]
1.3.2. 定义L₂范数惩罚
#定义L2范数惩罚(实现这一惩罚最方便的方法是对所有项求平方后并将它们求和)
def l2_penalty(w):return torch.sum(w.pow(2))/2 #将权重w的平方和除以2,除以2是为了方便计算梯度1.3.3. 定义训练代码实现
#定义训练代码实现
def train(lambd):w,b = init_params()net,loss = lambda x: d2l.linreg(x,w,b),d2l.squared_lossnum_epochs,lr = 100,0.003animator = d2l.Animator(xlabel="epochs",ylabel="loss",yscale="log",xlim= [5,num_epochs],legend=["train","test"])for epoch in range(num_epochs):for x,y in train_iter:#增加了L2范数惩罚项#广播机制使l2_penalty(w)成为一个长度为batch_size的向量l = loss(net(x),y) + lambd * l2_penalty(w)l.sum().backward()d2l.sgd([w,b],lr,batch_size)if (epoch+1)%5 ==0:animator.add(epoch+1,(d2l.evaluate_loss(net,train_iter,loss),d2l.evaluate_loss(net,test_iter,loss)))print("w的L2范数是:",torch.norm(w).item())
1.3.4. 不管正则化直接训练
#现在用`lambd = 0`禁用权重衰减后运行这个代码。
#注意,这里训练误差有了减少,但测试误差没有减少,这意味着出现了严重的过拟合。train(lambd= 0)#结果:
w的L2范数是: 13.981727600097656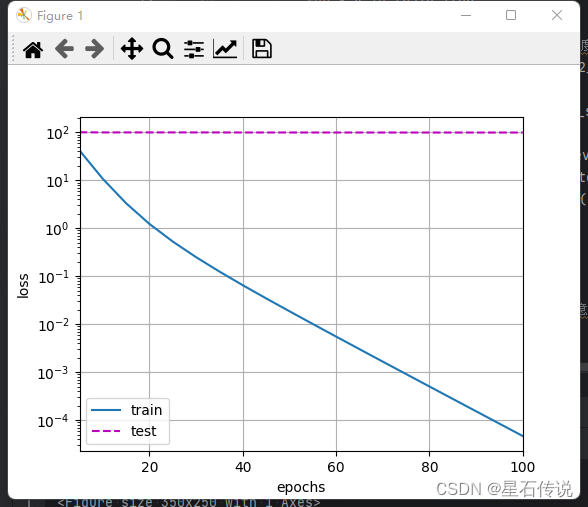
1.3.5. 使用权重衰减
#使用权重衰减来运行代码。
#注意,在这里训练误差增大,但测试误差减小。这正是我们期望从正则化中得到的效果。train(lambd= 3)#结果:
w的L2范数是: 0.3319331705570221d2l.plt.show()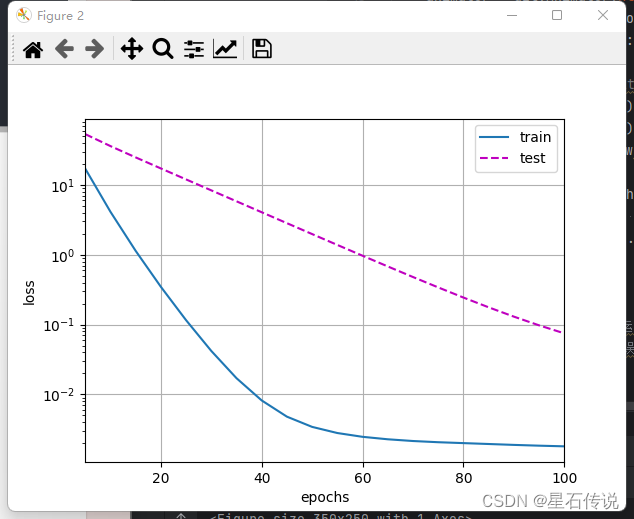
1.4. 简洁实现
深度学习框架为了便于我们使用权重衰减,将权重衰减集成到优化算法中,以便与任何损失函数结合使用。
#在下面的代码中,我们在实例化优化器时直接通过`weight_decay`指定weight decay超参数。
#默认情况下,PyTorch同时衰减权重和偏移。
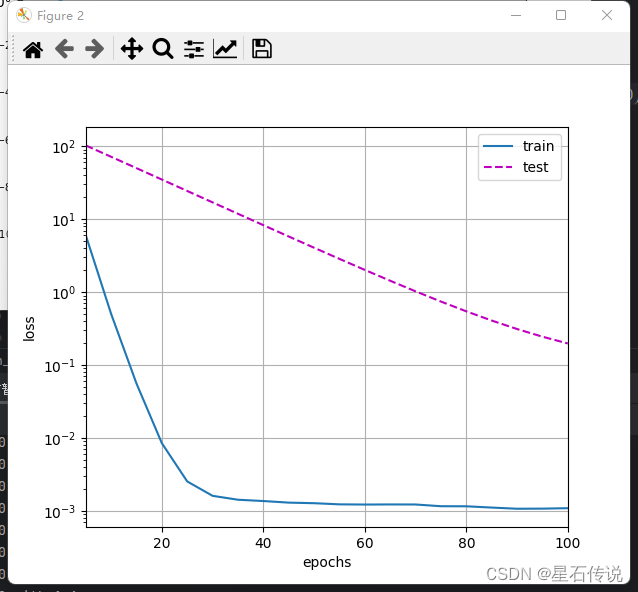
#这里我们只为权重设置了`weight_decay`,所以偏置参数$b$不会衰减。def train_concise(wd):net = nn.Sequential(nn.Linear(num_inputs,1))for param in net.parameters():param.data.normal_() #使用正态分布随机初始化参数loss = nn.MSELoss(reduction="none") #定义损失函数为均方误差损失num_epochs,lr = 100,0.003#偏置参数没有衰减trainer = torch.optim.SGD([{"params":net[0].weight,"weight_decay":wd},{"params":net[0].bias}],lr = lr) #net[0].weight表示模型的权重参数,net[0].bias表示模型的偏置参数。weight_decay参数用于设置权重衰减的强度。animator = d2l.Animator(xlabel="epochs",ylabel="loss",yscale="log",xlim=[5,num_epochs],legend=["train","test"])for epoch in range(num_epochs):for x,y in train_iter:trainer.zero_grad() #清零梯度,以防止梯度累积l = loss(net(x),y)l.mean().backward() #计算损失的平均值,并进行反向传播,计算梯度trainer.step() #更新模型的参数,执行一步优化器的更新if (epoch+1)%5 == 0:animator.add(epoch+1,(d2l.evaluate_loss(net,train_iter,loss),d2l.evaluate_loss(net,test_iter,loss)))print("w的L2范数:", net[0].weight.norm().item()) #打印模型权重的L2范数,用于评估模型的复杂度。train_concise(0)
train_concise(3)
d2l.plt.show()#结果:
w的L2范数: 13.411089897155762
w的L2范数: 0.3319282829761505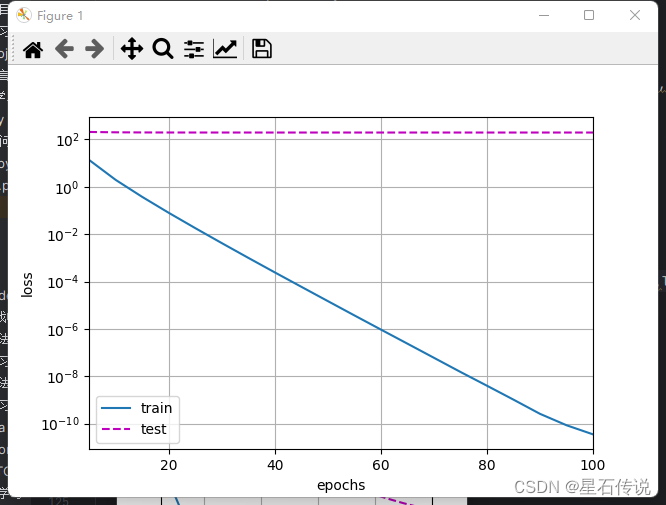
总结
为了有效防止模型的过拟合,降低模型的复杂度,提高泛化能力,本章简单记录了一种常见的正则化技术:权重衰减。简单来说权重衰减是通过在损失函数中添加一个正则化项来实现的。这个正则化项通常是模型参数的L2范数(平方和)或L1范数(绝对值和),通过限制模型参数的大小来防止过拟合。
我独泊兮其未兆,如婴儿之未孩,傫傫(lèi lèi)兮,若无所归。
–2023-10-2 进阶篇
相关文章:

深度学习——权重衰减(weight_decay)
深度学习——权重衰减(weight_decay) 文章目录 前言一、权重衰减1.1. 范数与权重衰减1.2. 高维线性回归1.3. 从零开始实现1.3.1.初始化模型参数1.3.2. 定义L₂范数惩罚1.3.3. 定义训练代码实现1.3.4. 不管正则化直接训练1.3.5. 使用权重衰减 1.4. 简洁实现 总结 前言…...

nignx如何部署让前端不用清缓存就可以部署
在Nginx中,可以使用以下方法来部署前端应用程序,使前端用户无需清空缓存即可进行部署: 1、使用版本号:在前端应用程序的构建过程中,可以添加一个独特的版本号到应用程序的名称中。每次部署时,将版本号更新…...

CSS3实现动画加载效果
<!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>加载效果</title><link rel"style…...

springboot定时任务Scheduled使用和弊端分析
1.springboot定时任务Scheduled使用说明: (1)创建定时任务类 import com.one.utils.DateUtil; import org.springframework.beans.factory.annotation.Autowired; import...

openGauss学习笔记-93 openGauss 数据库管理-访问外部数据库-oracle_fdw
文章目录 openGauss学习笔记-93 openGauss 数据库管理-访问外部数据库-oracle_fdw93.1 编译oracle_fdw93.2 使用oracle_fdw93.3 常见问题93.4 注意事项 openGauss学习笔记-93 openGauss 数据库管理-访问外部数据库-oracle_fdw openGauss的fdw实现的功能是各个openGauss数据库及…...

【Git】Git下载安装环境配置 下载速度慢的解决方案
这里写自定义目录标题 介绍一、下载官网下载镜像站 二、安装安装成功 三、Git三种界面介绍Git cmd界面展示git bash界面展示git GUI界面展示 四、环境配置配置流程1、打开环境变量界面2、添加环境变量 /删除环境变量3、在变量中找到Git\cmd的值就表示配置成功4、没有找到点击新…...

常见源协议介绍
开源协议(Open Source License)是一种法律文档,用于规定如何使用、修改和分发开源软件和其他开源项目的规则和条件。这些协议允许创作者或组织将其创造的代码或作品以开放源代码的形式共享给他人,以促进协作、创新和知识共享。常见…...
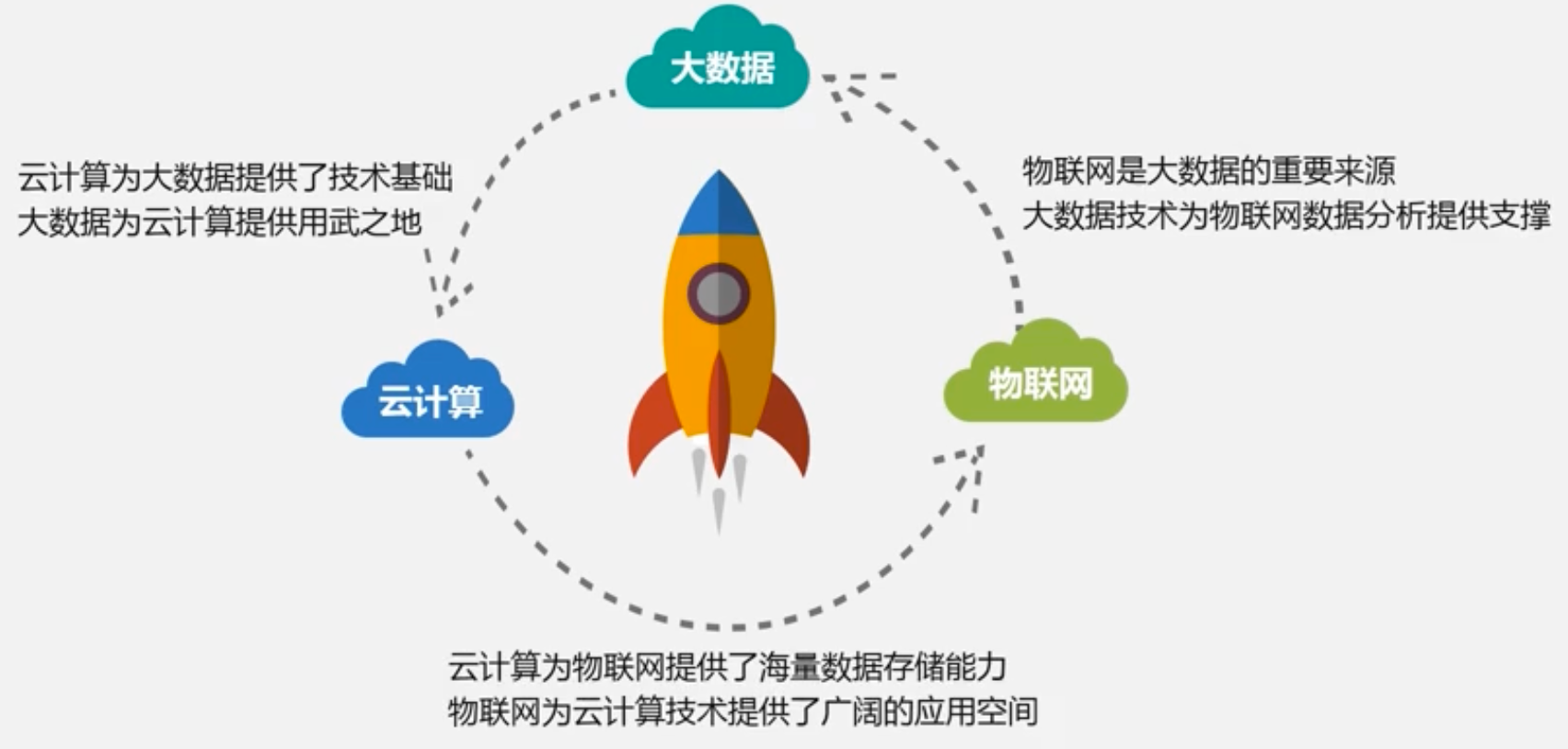
大数据概述(林子雨慕课课程)
文章目录 1. 大数据概述1.1 大数据概念和影响1.2 大数据的应用1.3 大数据的关键技术1.4 大数据与云计算和物联网的关系云计算物联网 1. 大数据概述 大数据的四大特点:大量化、快速化、多样化、价值密度低 1.1 大数据概念和影响 大数据摩尔定律 大数据由结构化和非…...
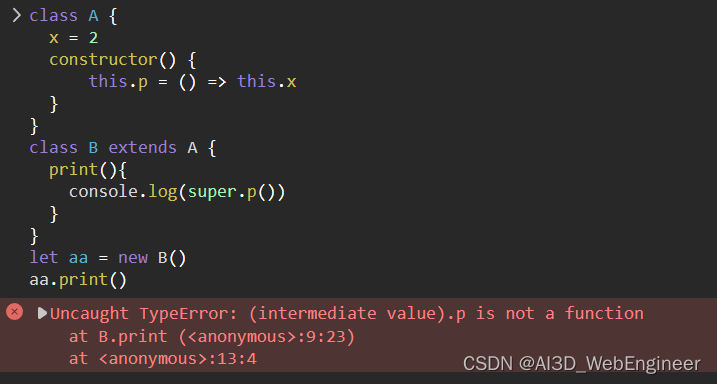
ES6 class类关键字super
super关键字 在 JavaSCript 中,能通过 extends 关键字去继承父类 super 关键字在子类中有以下用法: 当成函数调用 super() 作为 "属性查询" super.prop 和 super[expr] super() super 作为函数调用时,代表父类的构造函数。 ES6 要求…...
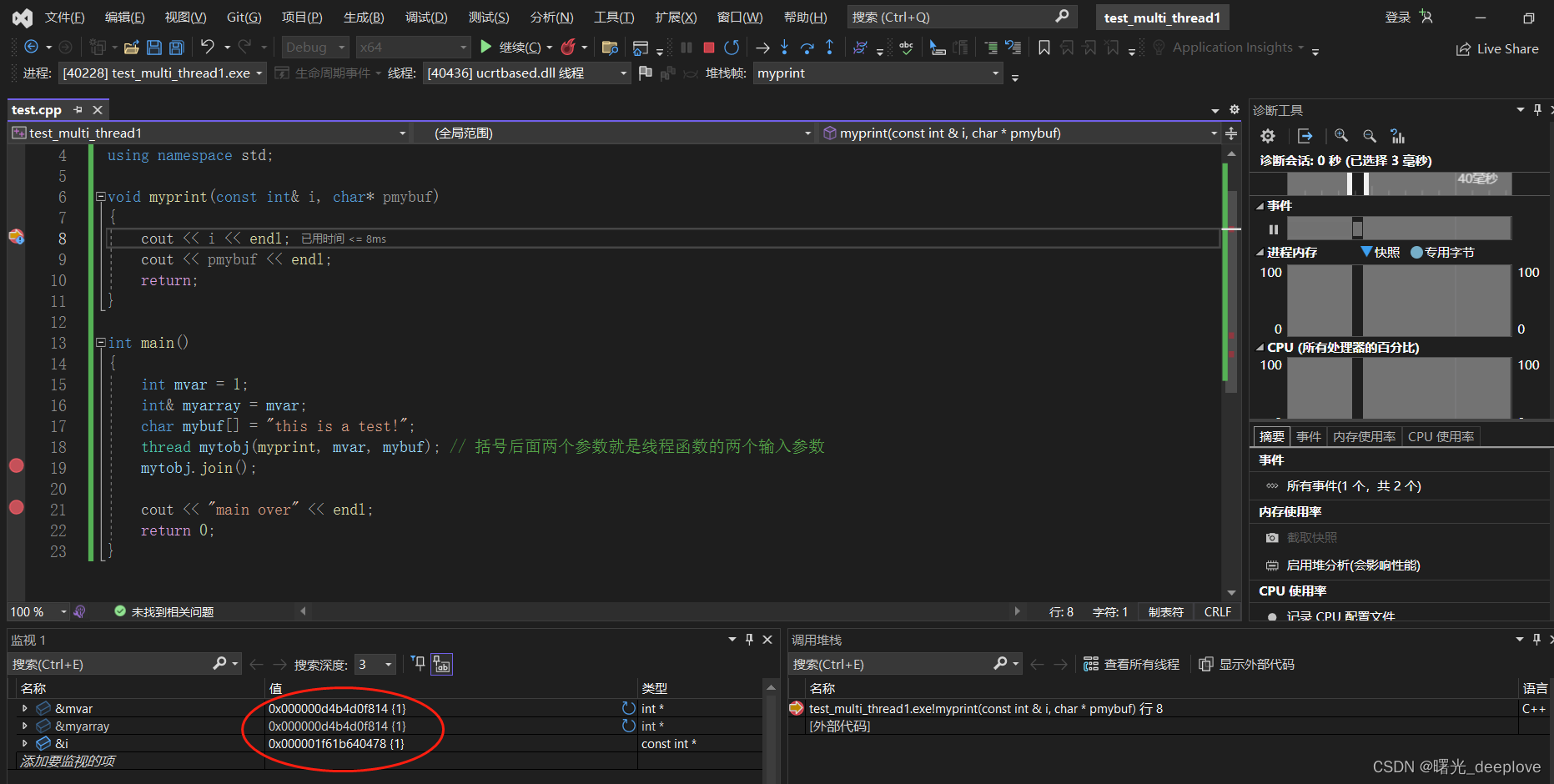
C++并发与多线程(4) | 传递临时对象作为线程参数的一些问题Ⅰ
一、陷阱1 写一个传递临时对象作为线程参数的示例: #include <iostream> #include <vector> #include <thread> using namespace std;void myprint(const int& i, char* pmybuf) {cout << i << endl;cout << pmybuf << endl;r…...

CentOS Integration SIG 正式成立
导读CentOS 董事会已批准成立 CentOS Integration Special Interest Group (SIG)。该小组旨在帮助那些在 Red Hat Enterprise Linux (RHEL) 或特别是其上游 CentOS Stream 上构建产品和服务的人员,验证其能否在未来版本中继续运行。 红帽 RHEL CI 工程师 Aleksandr…...
智能AI系统源码ChatGPT系统源码+详细搭建部署教程+AI绘画系统+已支持OpenAI GPT全模型+国内AI全模型
一、AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统,支持OpenAI GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作Chat…...

软考程序员考试大纲(2023)
文章目录 前言一、考试说明1.考试目标2.考试要求3.考试科目设置 二、考试范围考试科目1:计算机与软件工程基本知识1.计算机科学基础2.计算机系统基础知识3.系统开发和运行知识4.网络与信息安全基础知识5&am…...

【重拾C语言】七、指针(一)指针与变量、指针操作、指向指针的指针
目录 前言 七、指针 7.1 指针与变量 7.1.1 指针类型和指针变量 7.1.2 指针所指变量 7.1.3 空指针、无效指针 7.2 指针操作 7.2.1 指针的算术运算 7.2.2 指针的比较 7.2.3 指针的递增和递减 7.3 指向指针的指针 前言 指针是C语言中一个重要的概念正确灵活运用指针 可…...

Kafka源码简要分析
目录 一、生产者的初始化流程 二、生产者到缓冲队列的流程 三、Sender拉取数据到Kafka流程 四、消费者初始化 五、主题订阅原理 六、消费者抓取数据原理 七、消费者组初始化 八、消费者组消费流程 九、提交offset原理 一、生产者的初始化流程 首先获取事务id和客户端…...

react 按住ctrl键,点击时会出现菜单的问题修复
问题描述:我需要按住crtl键,然后鼠标点击后做一些逻辑操作,但是出现如下问题 问题一:按住ctrl键后,点击时不触发click事件,只触发 mousedown和mouseup事件。 问题二:按住ctrl键点击时出现菜单…...

【虚拟机栈】
文章目录 1. 虚拟机栈概述2. 局部变量表(Local Variables)3. 操作数栈4. 动态链接4.1 方法的调用:解析与分配 5. 方法返回地址6. 栈的相关面试题 1. 虚拟机栈概述 每个线程在创建时都会创建一个虚拟机栈,其内部保存一个个的栈帧(Stack Frame…...
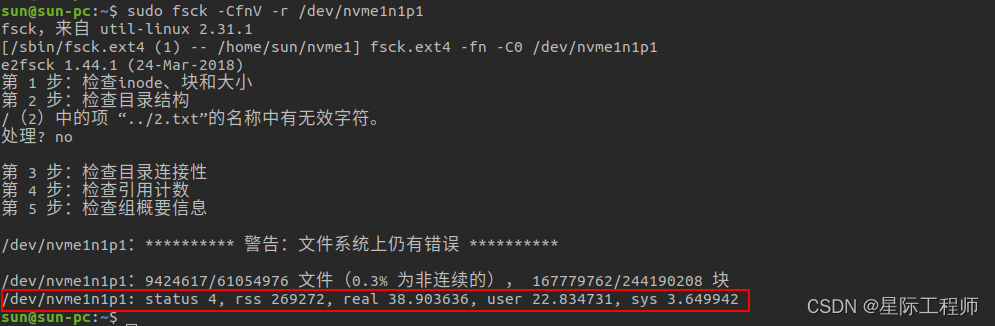
Linux系列讲解 —— 【fsck】检查并修复Linux文件系统
当文件系统出现损坏时,例如文件无法查看,删除等,可以使用 fsck(File System Consistency Check)进行修复。但是需要注意fsck在修复时,如果检查出某个文件有问题,可能会向用户请求删除。所以&…...

gitlab突然提示我要输入密码了。
用了很长时间的一个gitlab库,今天提交代码的时候突然提示我输入密码了,并且用户还是gitxx.xx.xx.xx的,瞬间懵逼。 想想原因,可能是因为我不久前设置了本地对另外一个git库的远程访问,用的是ssh,操作过程中可…...
)
业务测试常见问题(一)
如何多维度的分析一个需求? 功能维度:需求中所描述的功能是否实现,与用户的需求是否一致,是否完整符合用户的需求等。 安全性维度:是否有安全漏洞,是否存在未授权访问漏洞等,以保证系统的安全性…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
