当前位置： 首页 > news >正文

【虚拟机】NAT 模式下访问外网

news 2026/2/8 11:14:55

目录

一、NAT 模式的作用原理

二、配置 NAT 模式实现外网访问

1、配置NAT模式的网段

2、虚拟机选择 VMnet8 网卡

3、IP地址设为自动分配

一、NAT 模式的作用原理

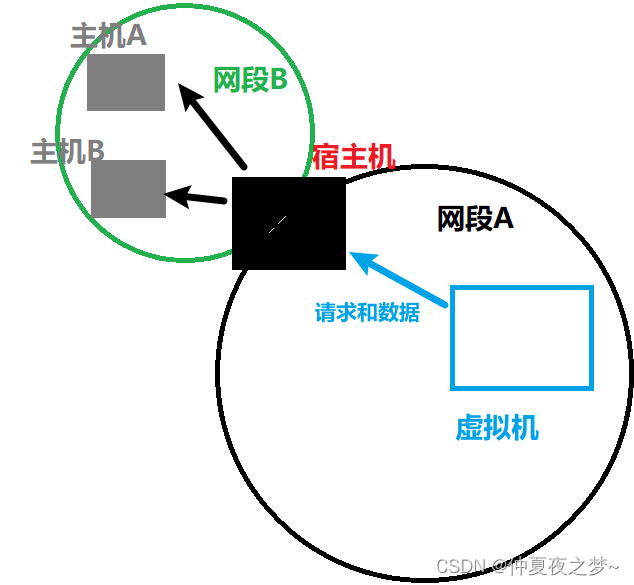
NAT模式下，虚拟机的系统会把宿主机当作一个大路由器，发送的网络请求和数据都是先发给宿主机的虚拟网卡 VMnet8，然后再通过宿主机的无线网卡发往外网。宿主机相当于有了三张网卡，一张是真实网卡，两张是虚拟网卡(一张用于桥接，一张用于NAT)。

但是经过NAT的地址转换以后，站在外人的角度，看到的只是宿主机的IP地址，因为宿主机被当作一个路由器，此时宿主机和虚拟机构成一个网段，宿主机和外部网络构成一个网段。NAT模式最大的特点就在于，IP地址和子网掩码是自动分配的，虚拟机可以ping通宿主机，但是宿主机无法ping通虚拟机。

二、配置 NAT 模式实现外网访问

1、配置NAT模式的网段

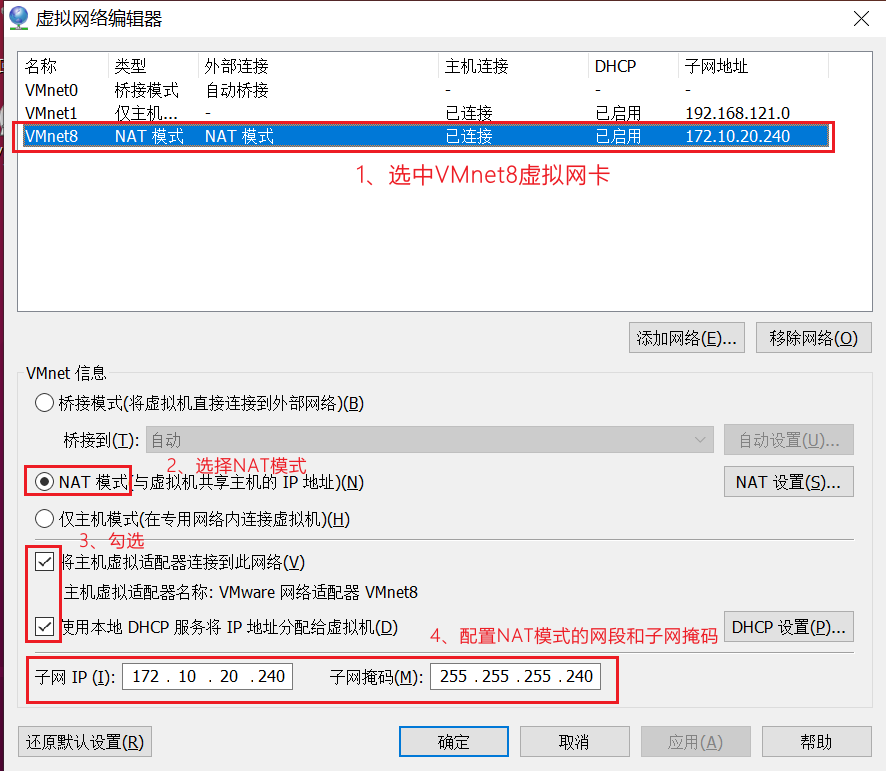
既然是把宿主机当做是一个路由器，那么就需要保证 NAT模式下，虚拟机与宿主机是在同一个网段，首先看一下宿主机当前可访问外网的IP是多少。

将 IP 地址和子网掩码按位与便可以得到对应的网段和子网掩码: 

网段172.20.10.240
子网掩码255.255.255.240

打开虚拟机网络编辑器

按如下步骤配置（核心是最后的网段设置），现在 VMnet8 网卡已经配置成了我们期望的网段

2、虚拟机选择 VMnet8 网卡

上面只是针对 VMnet8 网卡做了一些基本的配置，但还需要虚拟机选择 VMnet8 网卡（虚拟机—设置—网络适配器）

3、IP地址设为自动分配

NAT模式下如果手动分配IP，无法连接到外网

相关文章：

【虚拟机】NAT 模式下访问外网

目录 一、NAT 模式的作用原理 二、配置 NAT 模式实现外网访问 1、配置NAT模式的网段 2、虚拟机选择 VMnet8 网卡 3、IP地址设为自动分配 一、NAT 模式的作用原理 NAT模式下，虚拟机的系统会把宿主机当作一个大路由器，发送的网络请求和数据都是先发给…...

编程日记 2023/10/9 8:23:01

React 入门笔记

前言 国庆值班把假期拆了个稀碎, 正好不用去看人潮人海, 趁机会赶个晚集入门一下都火这么久的 React 前端技术. 话说其实 n 年前也了解过一丢丢来着, 当时看到一上来就用 JS 写 DOM 的套路直接就给吓退了, 扭头还去看 Vue 了🤣, 现在从市场份额 社区活度来看, 确实…...

编程日记 2023/10/9 8:21:59

Ubuntu MySQL

在安装前，首先看你之前是否安装过，如果安装过，但是没成功，就要先卸载。 一、卸载 1.查看安装 dpkg --list | grep mysql 有东西，就说明您之前安装过mysql。 2.卸载 先停掉server sudo systemctl stop mysql.servic…...

编程日记 2023/10/9 8:20:57

大数据软件系统开发框架

大数据处理框架是用于处理大规模数据集的软件工具和平台，它们可以帮助分析、存储和处理庞大的数据量。以下是一些常见的大数据处理框架，希望对大家有所帮助。北京木奇移动技术有限公司，专业的软件外包开发公司，欢迎交流合作。 1.A…...

编程日记 2023/10/9 8:19:56

rust变量

一 、变量定义 （一）语法格式 使用let关键字定义变量 let varname: type value; 如，let a: i32 78;也可以不显式指定类型 let varname value; 如，let a 78;一些例子 1.布尔 let t true; let f: bool false;2.整数 let a …...

编程日记 2023/10/9 8:18:54

蓝桥杯---第一讲 递归与递推

文章目录 前言Ⅰ. 递归实现指数型枚举0x00 算法思路0x00 代码书写0x00 思考总结 Ⅱ. 递归实现排列型枚举0x00 算法思路0x01代码书写0x02 思考总结 Ⅲ. 简单斐波那契0x00 算法思路0x01 代码书写 Ⅳ. 费解的开关0x00 算法思路0x01 代码书写 Ⅴ. 递归实现组合型枚举0x00 算法思路0…...

编程日记 2023/10/9 8:17:53

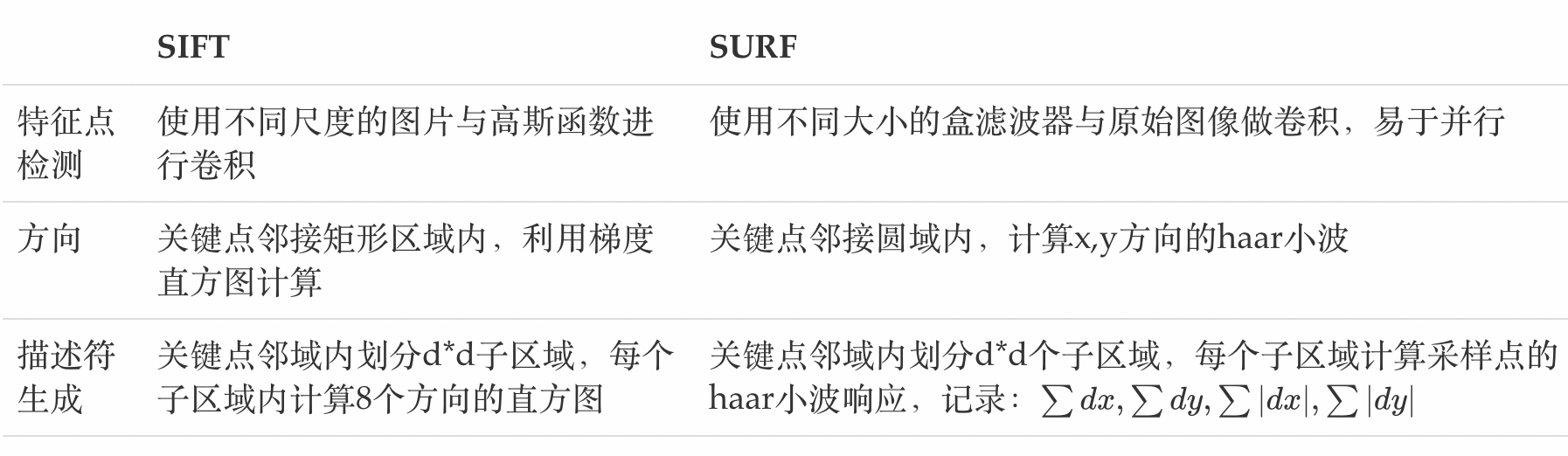
OpenCV 15(SIFT/SURF算法)

一、SIFT Harris和Shi-Tomasi角点检测算法，这两种算法具有旋转不变性，但不具有尺度不变性，以下图为例，在左侧小图中可以检测到角点，但是图像被放大后，在使用同样的窗口，就检测不到角点了。 尺度…...

编程日记 2023/10/9 8:16:51

前端二维码图片解析图片识别/网络图片解析成链接/图片网络链接转本地链接(Js/Vue/Jquery)

注&#xff1a;需要用到canvas/jsqr/jquery&#xff01; 1、远程图片链接本地化 页面&#xff1a; <!-- 识别二维码用的 canvas--> <canvas class"canvas" ref"canvas" style"display: none"></canvas> 1.创建图片 get2: fu…...

编程日记 2023/10/9 8:15:51

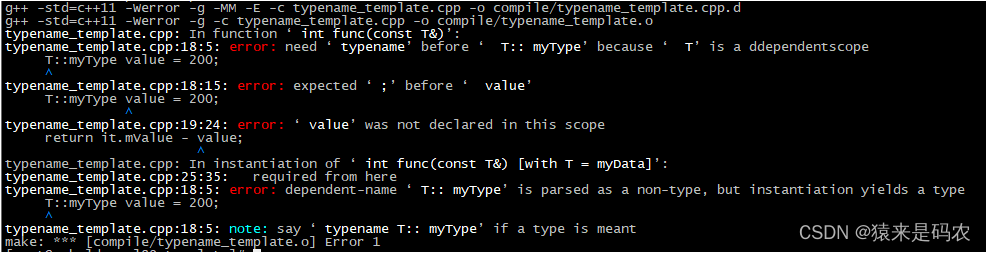
模板中的依赖类型使用 --- typename

依赖类型&#xff0c;顾名思义就是依赖于模板参数的类型&#xff0c;在使用这种类型时&#xff0c;必须使用 typename&#xff0c;否则编译器是无法知道是在使用类型&#xff0c;还是类的成员&#xff08;因为类的静态成员的使用方法也是T::xxx&#xff0c;这跟某个类中的类型的…...

编程日记 2023/10/9 8:14:50

git 同时配置 gitee github

git 同时配置 gitee github 1、 删除C:\Users\dell\.ssh目录。 在任意目录右击——》Git Bash Here&#xff0c;打开Git Bash窗口&#xff0c;下方命令在Git Bash窗口输入。 2、添加git全局范围的用户名和邮箱 git config --global user.email "609612189qq.com" …...

编程日记 2023/10/9 8:13:48

2023.10.8 面试

面试工作1年的程序员 看到生涩才入职场不久的面试者&#xff0c;为人也相对诚恳的模样&#xff0c;我对此是很欣赏的态度。 因为完全看到了自己毕业1年时的场景。 简历上写的事情&#xff0c;讨论起来&#xff0c;描述不清楚&#xff0c;为此感到遗憾&#xff0c;因我本人也会…...

编程日记 2023/10/9 8:12:46

【前端】js实现队列功能 先进后出 先进先出 等

也可以定义一个定时器 不断的去取队列 执行任务 用一个flag定义队列正在执行中, 如果没有执行 则定时器不断的去调用队列,(因为会随时添加一个任务到队列中) 队列任务结束后 自动取下一个队列 也可以边加队列 边取 队列定义 function Queue() {//初始化队列&#xff08;使用…...

编程日记 2023/10/9 8:11:46

07.数据持久化之文件操作

1. 文件操作 计算机的文件&#xff0c;就是存储在某种 长期储存设备 上的一段 数据 长期存储设备包括&#xff1a;硬盘、U 盘、移动硬盘、光盘… 文本文件和二进制文件 文本文件 可以使用 文本编辑软件 查看本质上还是二进制文件例如&#xff1a;python 的源程序 二进制文件…...

编程日记 2023/10/9 8:09:41

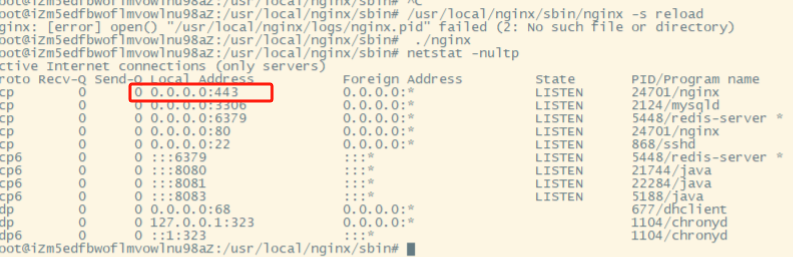
nginx开启https配置之后网页无法访问问题处理

背景说明 最近新购服务器部署nginx之后按照之前的方式部署前端项目并配置https之后访问页面显示:无法访问.新的服务器ECS系统和之前相同,nginx安装方式也相同,nginx配置方式也是相同.但是访问还是显示无法访问.下面简单记录一下问题处理过程. 处理过程 1.https访问之后无法访问…...

编程日记 2023/10/9 8:08:39

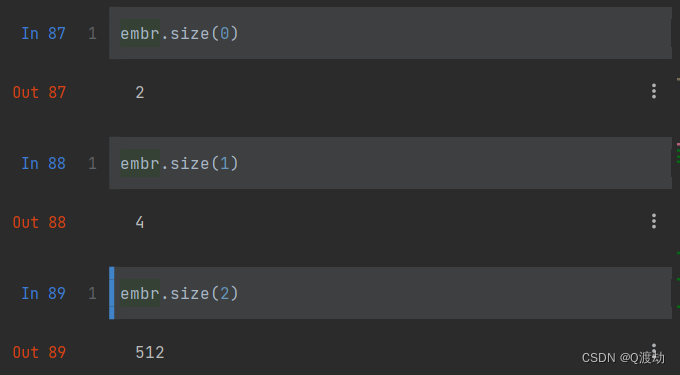
文本嵌入层

目录 1、文本嵌入层的作用 2、代码演示 3、构建Embeddings类来实现文本嵌入层 1、文本嵌入层的作用 无论是源文本嵌入层还是目标文本嵌入&#xff0c;都是为了将文本词汇中的数字表示转变为向量表示&#xff0c;希望在这样的高维空间中捕捉词汇之间的关系 2、代码演示 Emb…...

编程日记 2023/10/9 8:06:38

如何搭建自动化测试框架

关于测试框架的好处&#xff0c;比如快速回归提高测试效率&#xff0c;提高测试覆盖率等这里就不讨论了。这里主要讨论自动化框架包含哪些内容&#xff0c;以及如何去设计一个测试框架。 1. 什么是自动化测试框架&#xff1f; 它是由一个或多个自动化测试基础模块、自动化测试…...

编程日记 2023/10/9 8:05:37

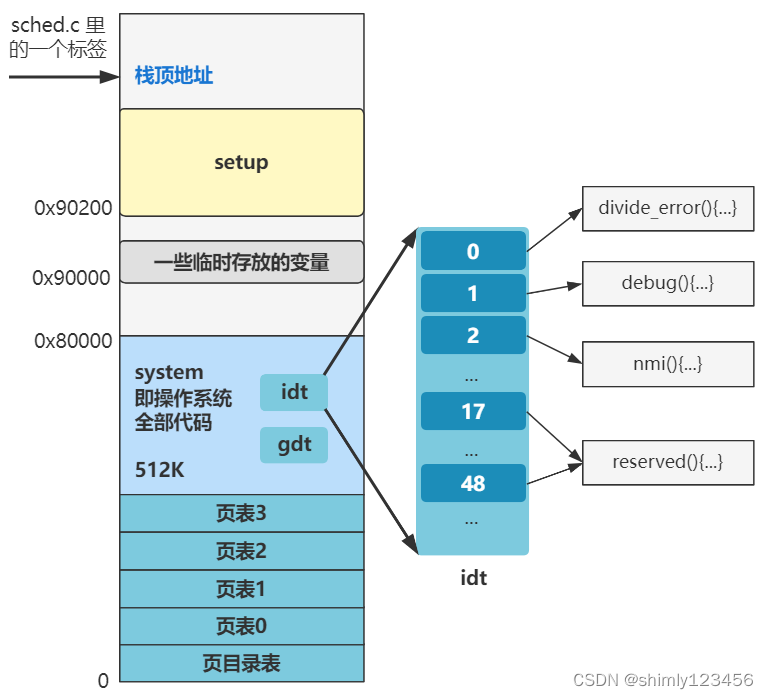
抄写Linux源码(Day17：你的键盘是什么时候生效的？)

回忆我们需要做的事情&#xff1a; 为了支持 shell 程序的执行&#xff0c;我们需要提供&#xff1a; 1.缺页中断(不理解为什么要这个东西&#xff0c;只是闪客说需要&#xff0c;后边再说) 2.硬盘驱动、文件系统 (shell程序一开始是存放在磁盘里的&#xff0c;所以需要这两个东…...

编程日记 2023/10/9 8:04:33

在原生html中使用less

引入less <link rel"stylesheet/less" href"./lessDemo.less" /><script src"./js/less.min.js"></script> less.min.js文件下载地址:https://github.com/less/less.js 注意&#xff1a;less文件在前&#xff0c;js文件在后…...

编程日记 2023/10/9 8:03:31

【Qt】顶层窗口和普通窗口区别以及用法

区别 在Qt项目开发中&#xff0c;经常会用到窗体控件用于显示及数据操作和其他交互等。 但&#xff0c;窗体分为顶层窗口&#xff08;Top-level Window&#xff09;和普通窗口&#xff08;Regular Window&#xff09;。 他们之间是有区别的&#xff0c;包括在项目实际中的用法…...

编程日记 2023/10/9 8:01:26

qt开发从入门到实战2

以下是本人学习笔记 原视频&#xff1a;最新QT从入门到实战完整版|传智教育 qt开发从入门到实战1 练习示例 设计一个按钮&#xff0c;点击时弹出新窗口&#xff0c;再次点击时新窗口关闭 // exerciseQWidget* second_window new QWidget();QPushButton* btn3 new QPushBu…...

编程日记 2023/10/9 8:00:24

Leetcode 3576. Transform Array to All Equal Elements

Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接&#xff1a;3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到&#xf…...

编程新知 2025/9/17 7:25:07

React19源码系列之 事件插件系统

事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

编程新知 2026/2/7 8:31:55

用docker来安装部署freeswitch记录

今天刚才测试一个callcenter的项目&#xff0c;所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

编程新知 2026/2/1 3:20:44

聊一聊接口测试的意义有哪些？

目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开&#xff0c;首…...

编程新知 2025/10/14 6:46:13

Yolov8 目标检测蒸馏学习记录

yolov8系列模型蒸馏基本流程&#xff0c;代码下载&#xff1a;这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中&#xff0c;**知识蒸馏&#xff08;Knowledge Distillation&#xff09;**被广泛应用&#xff0c;作为提升模型…...

编程新知 2026/1/25 7:20:01

如何更改默认 Crontab 编辑器 ？

在 Linux 领域中&#xff0c;crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用&#xff0c;用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益&#xff0c;允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

编程新知 2026/1/30 3:27:35

解读《网络安全法》最新修订，把握网络安全新趋势

《网络安全法》自2017年施行以来&#xff0c;在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂&#xff0c;网络攻击、数据泄露等事件频发&#xff0c;现行法律已难以完全适应新的风险挑战。 2025年3月28日&#xff0c;国家网信办会同相关部门起草了《网络安全…...

编程新知 2026/1/31 4:40:38

Python 高效图像帧提取与视频编码：实战指南

Python 高效图像帧提取与视频编码：实战指南 在音视频处理领域，图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库（如 OpenCV、FFmpeg、PyAV），可以高效处理视频流，实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程，提高处理…...

编程新知 2025/8/31 18:02:53

华为OD最新机试真题-数组组成的最小数字-OD统一考试（B卷）

题目描述 给定一个整型数组，请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3，则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组，0<数组长度<= 100，0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

编程新知 2025/9/21 23:43:15

多元隐函数 偏导公式

我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式&#xff0c;给定一个隐函数关系&#xff1a; F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 &#x1f9e0; 目标&#xff1a; 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z​、 …...

编程新知 2025/9/19 5:31:38