AM@无穷小和无穷大
文章目录
- abstract
- 本文符号说明
- 无穷小
- 无穷小和自变量变化过程
- 无穷小和函数极限的关系定理👺
- 证明
- 无穷大
- 无穷大不是数
- 极限无穷大的说法
- 证明函数极限为无穷大
- 无穷大和无穷小见的关系定理
- 无穷小@无穷大的运算法则
abstract
- 无穷小和无穷大的概念和相关性质
本文符号说明
- 自变量 x x x趋于 ∗ {*} ∗(表示有限值 x 0 x_0 x0,或无穷 ∞ \infin ∞)的变化过程 x → ∗ x\to{*} x→∗表示: x → x 0 x\to{x_0} x→x0或 x → ∞ x\to{\infin} x→∞
无穷小
- 若函数 lim x → ∗ f ( x ) = 0 \lim\limits_{x\to{*}}f(x)=0 x→∗limf(x)=0,则称 f ( x ) f(x) f(x)为 x → ∗ x\to{*} x→∗时的无穷小
- 特别地,以0为极限的数列 { x n } \set{x_n} {xn}称为 n → ∞ n\to{\infin} n→∞时的无穷小
- 从定义可以看出,无穷小是对具有某种性质的函数的称呼,而不是指很小(无穷小)的数
- Note:
- 记无穷小为 α \alpha α.无穷小 α \alpha α的精髓在于, x → ∗ x\to{*} x→∗的极限过程中可以无限接近0,即 ∣ α ∣ |\alpha| ∣α∣小于任意给定的正数 ϵ ( ϵ > 0 ) \epsilon(\epsilon>0) ϵ(ϵ>0)
- 可见,任何非0的常数(或者常数函数 y = a ( a ≠ 0 ) y=a(a\neq{0}) y=a(a=0)都无法做到这一点
- 而常数 0 0 0(或者 y = 0 y=0 y=0)可以满足无穷小的条件 ∣ 0 ∣ < ϵ |0|<\epsilon ∣0∣<ϵ,因此是无穷小,并且在任意极限过程 ( x → ∗ ) (x\to{*}) (x→∗)都是无穷小,因此 0 0 0有特殊地位
- 无穷小可以称为无穷小函数,更具体地称过程 x → ∗ x\to{*} x→∗的无穷小函数
- 有些函数不可能是无穷小,例如 y = 1 + 1 x ( x > 0 ) y=1+\frac{1}{x}(x>0) y=1+x1(x>0),其定义域内任何自变量过程的函数极限不小于1
- 例: lim x → 1 ( x − 1 ) = 0 \lim\limits_{x\to1}(x-1)=0 x→1lim(x−1)=0,所以 x − 1 x-1 x−1是 x → 1 x\to{1} x→1时的等价无穷小
无穷小和自变量变化过程
- 0 0 0以外的任何无穷小都有其对一个的变化过程 x → ∗ x\to{*} x→∗
- 这和极限相仿,提到极限一定有其对应的自变量变化过程
- 无穷小参与运算或构成的式子中,要有一致的自变量变化过程
- 无穷小是函数,因此也可以和其他一般函数一起构成其他函数解析式,只不过无穷小要强调趋于0时对应的自变量变化过程 ( x → ∗ ) (x\to{*}) (x→∗),脱离了变化过程,某些 α \alpha α相关等式不再成立
无穷小和函数极限的关系定理👺
- 在自变量的同一个变化过程 x → ∗ x\to{*} x→∗中,函数 f ( x ) f(x) f(x)具有极限 A A A的充要条件是 f ( x ) = A + α f(x)=A+\alpha f(x)=A+α, α \alpha α是无穷小
- 其中 A + α A+\alpha A+α是函数而不是常数
证明
-
以 x → x 0 x\to{x_0} x→x0为例,主要采用极限和无穷小的定义进行推理( x → ∞ x\to{\infin} x→∞类似)
-
必要性:设 lim x → x 0 f ( x ) = A \lim\limits_{x\to{x_0}}f(x)=A x→x0limf(x)=A,
- 则由极限定义: ∀ ϵ > 0 \forall{\epsilon>0} ∀ϵ>0, ∃ δ > 0 \exist{\delta>0} ∃δ>0,当 0 < ∣ x − x 0 ∣ < δ 0<|x-x_0|<\delta 0<∣x−x0∣<δ时,有 ∣ f ( x ) − A ∣ < ϵ |f(x)-A|<\epsilon ∣f(x)−A∣<ϵ;
- 令 α = f ( x ) − A \alpha=f(x)-A α=f(x)−A,则 ∣ α ∣ < ϵ |\alpha|<\epsilon ∣α∣<ϵ,即 ∣ α − 0 ∣ < ϵ |\alpha-0|<\epsilon ∣α−0∣<ϵ所以极限定义, lim x → x 0 α = 0 \lim\limits_{x\to{x_0}}\alpha=0 x→x0limα=0
- 所以 α \alpha α是 x → x 0 x\to{x_0} x→x0时的无穷小,且 f ( x ) = A + α f(x)=A+\alpha f(x)=A+α
- 或者说, f ( x ) f(x) f(x)等于它的 ( x → x 0 ) (x\to{x_0}) (x→x0)时的极限 A A A与一个无穷小 α \alpha α之和,其中 α \alpha α可以取 f ( x ) − A f(x)-A f(x)−A
- Note:
- 从极限运算的角度:则 lim x → x 0 α \lim\limits_{x\to{x_0}}\alpha x→x0limα= lim x → x 0 ( f ( x ) − A ) \lim\limits_{x\to{x_0}}(f(x)-A) x→x0lim(f(x)−A)= lim x → x 0 f ( x ) − lim x → x 0 A \lim\limits_{x\to{x_0}}f(x)-\lim\limits_{x\to{x_0}}A x→x0limf(x)−x→x0limA= A − A A-A A−A=0也可说明 α \alpha α是 x → x 0 x\to{x_0} x→x0时的无穷小
-
充分性:设 f ( x ) f(x) f(x)= A + α A+\alpha A+α
(1),其中 A A A是常数, α \alpha α是 x → x 0 x\to{x_0} x→x0时的无穷小- 定义法证明
- 显然 ∣ f ( x ) − A ∣ = ∣ α ∣ |f(x)-A|=|\alpha| ∣f(x)−A∣=∣α∣
- 因为 α → 0 ( x → x 0 ) \alpha\to{0}(x\to{x_0}) α→0(x→x0)所以 ∀ ϵ > 0 \forall{\epsilon>0} ∀ϵ>0, ∃ δ > 0 \exist{\delta>0} ∃δ>0,当 0 < ∣ x − x 0 ∣ < δ 0<|x-x_0|<\delta 0<∣x−x0∣<δ时, ∣ α ∣ < ϵ |\alpha|<\epsilon ∣α∣<ϵ,即 ∣ f ( x ) − A ∣ < ϵ |f(x)-A|<\epsilon ∣f(x)−A∣<ϵ
- 所以 lim x → x 0 f ( x ) = A \lim\limits_{x\to{x_0}}f(x)=A x→x0limf(x)=A
- 极限运算法:对
(1)两边取极限: lim x → x 0 f ( x ) \lim\limits_{x\to{x_0}}f(x) x→x0limf(x)= lim x → x 0 ( A + α ) \lim\limits_{x\to{x_0}}(A+\alpha) x→x0lim(A+α)= lim x → x 0 A \lim\limits_{x\to{x_0}}A x→x0limA+ lim x → x 0 α \lim\limits_{x\to{x_0}}\alpha x→x0limα= A + 0 A+0 A+0= A A A
- 定义法证明
无穷大
- 若 x → ∗ x\to{*} x→∗时, ∣ f ( x ) ∣ |f(x)| ∣f(x)∣可以大于预先给定的任意大正数 M M M,则 f ( x ) f(x) f(x)是 x → ∗ x\to{*} x→∗时的无穷大
- 或者精确地说:
- 设 f ( x ) f(x) f(x)在 x 0 x_0 x0的某个去心领域 U ( x 0 , δ ) ˚ {\mathring {U(x_0,\delta)}} U(x0,δ)˚(或 ∣ x ∣ > N ∈ N + |x|>N\in\mathbb{N}_{+} ∣x∣>N∈N+)内有定义
- 若 ∀ M \forall{M} ∀M, ∃ δ > 0 \exist{\delta>0} ∃δ>0(或 ∃ X > 0 \exist X>0 ∃X>0),当 x ∈ U ( x 0 , δ ) ˚ x\in{\mathring {U(x_0,\delta)}} x∈U(x0,δ)˚或( ∣ x ∣ > X |x|>X ∣x∣>X),总有 ∣ f ( x ) ∣ > M |f(x)|>M ∣f(x)∣>M,则称 f ( x ) f(x) f(x)是 x → x 0 x\to{x_0} x→x0(或 x → ∞ x\to{\infin} x→∞)时的无穷大
无穷大不是数
- 无穷大 ∞ \infin ∞不是数,不同于很大的数(常数),而是强调自变量极限变化过程 ( x → ∗ ) (x\to{*}) (x→∗)的函数,且 ( x → ∗ ) (x\to{*}) (x→∗)时函数值要多大有多大
极限无穷大的说法
-
按照函数极限的定义, x → ∗ x\to{*} x→∗时是无穷大的函数 f ( x ) f(x) f(x)的极限是不存在的(无穷大不是数)
-
为了便于叙述函数的这一性态,也称呼为函数的极限是无穷大的
-
总之:极限无穷大仍要归为极限不存在的大类当中,
- "极限无穷大"是"极限不存在且函数值趋于无穷"的简称
- 记为 lim x → ∗ f ( x ) = ∞ \lim\limits_{x\to{*}}f(x)=\infin x→∗limf(x)=∞
- 例
- f ( x ) = x 2 f(x)=x^2 f(x)=x2, lim x → ∞ x 2 = ∞ \lim\limits_{x\to{\infin}}x^2=\infin x→∞limx2=∞
- f ( x ) = 1 x f(x)=\frac{1}{x} f(x)=x1, lim x → 0 1 x = ∞ \lim\limits_{x\to{0}}\frac{1}{x}=\infin x→0limx1=∞
-
若将定义中的 ∣ f ( x ) ∣ > M |f(x)|>M ∣f(x)∣>M替换为 f ( x ) > M f(x)>M f(x)>M(或 f ( x ) < − M f(x)<-M f(x)<−M),则记为 lim x → ∗ f ( x ) = + ∞ \lim\limits_{x\to{*}}f(x)=+\infin x→∗limf(x)=+∞ ( lim x → ∗ f ( x ) = − ∞ ) (\lim\limits_{x\to{*}}f(x)=-\infin) (x→∗limf(x)=−∞)
证明函数极限为无穷大
- 极限无穷大本质上是极限不存在的情况,因此和证明极限存在时的情形有所不同,这里不再借助 ∀ ϵ > 0 \forall{\epsilon}>0 ∀ϵ>0来刻画 x → ∗ x\to{*} x→∗时函数和有限且确定的极限值无限接近,而采用 ∀ M > 0 \forall{M}>0 ∀M>0来体现 x → ∗ x\to{*} x→∗时的无穷大含义
- 证明 lim x → ∗ f ( x ) = ∞ \lim\limits_{x\to{*}}f(x)=\infin x→∗limf(x)=∞的思路是,设 ∀ M > 0 \forall{M>0} ∀M>0, ∃ X > 0 \exist{X}>0 ∃X>0,当( x x x满足) 0 < ∣ x − x 0 ∣ < δ 0<|x-x_0|<\delta 0<∣x−x0∣<δ(或 x > X x>X x>X)时 ∣ f ( x ) ∣ > M |f(x)|>M ∣f(x)∣>M
(1)- 从
(1)求出 x x x的取值范围并选定一个确定的 X X X值(或 δ \delta δ),来说明 f ( x ) f(x) f(x)在 x → ∗ x\to{*} x→∗时要多大有多大,即 lim x → ∗ f ( x ) = ∞ \lim\limits_{x\to{*}}f(x)=\infin x→∗limf(x)=∞
- 从
- 例
- 令 f ( x ) = 1 x − 1 f(x)=\frac{1}{x-1} f(x)=x−11证明 lim x → 1 f ( x ) = ∞ \lim\limits_{x\to{1}}f(x)=\infin x→1limf(x)=∞
- 证明:设 ∀ M > 0 \forall{M>0} ∀M>0,令 ∣ f ( x ) ∣ > M |f(x)|>M ∣f(x)∣>M,即 ∣ 1 x − 1 ∣ > M |\frac{1}{x-1}|>M ∣x−11∣>M,即 ∣ x − 1 ∣ < 1 M |x-1|<\frac{1}{M} ∣x−1∣<M1
- 令 δ = 1 M \delta=\frac{1}{M} δ=M1,则当 x x x满足 0 < ∣ x − 1 ∣ < δ 0<|x-1|<\delta 0<∣x−1∣<δ时有 ∣ 1 x − 1 ∣ > M |\frac{1}{x-1}|>M ∣x−11∣>M成立,从而 lim x → 1 f ( x ) = ∞ \lim\limits_{x\to{1}}f(x)=\infin x→1limf(x)=∞
- 可见 x = 1 x=1 x=1时函数 y = 1 x − 1 y=\frac{1}{x-1} y=x−11的图形的铅直渐近线
无穷大和无穷小见的关系定理
-
在自变量的同一个变化过程 x → ∗ x\to{*} x→∗中,函数 f ( x ) f(x) f(x)为无穷大,则 1 f ( x ) \frac{1}{f(x)} f(x)1是无穷小;
- 反之,若 f ( x ) f(x) f(x)是无穷小,且 f ( x ) ≠ 0 f(x)\neq{0} f(x)=0,则 1 f ( x ) \frac{1}{f(x)} f(x)1为无穷大
-
证:以 x → x 0 x\to{x_0} x→x0为例( x → ∞ x\to\infin x→∞类似)
-
设 lim x → x 0 f ( x ) = ∞ \lim\limits_{x\to{x_0}}f(x)=\infin x→x0limf(x)=∞,则 ∀ M > 0 \forall{M>0} ∀M>0, ∃ δ > 0 \exist{\delta>0} ∃δ>0,当 0 < ∣ x − x 0 ∣ < δ 0<|x-x_0|<\delta 0<∣x−x0∣<δ时,有 ∣ f ( x ) ∣ > M |f(x)|>M ∣f(x)∣>M
-
则 ∣ 1 f ( x ) ∣ < 1 M |\frac{1}{f(x)}|<\frac{1}{M} ∣f(x)1∣<M1,令 ϵ = 1 M \epsilon=\frac{1}{M} ϵ=M1,因为 M M M可以取任何正数,所以 ϵ \epsilon ϵ也可取任何值,且总有 ∣ 1 f ( x ) ∣ < ϵ |\frac{1}{f(x)}|<\epsilon ∣f(x)1∣<ϵ,从而 lim x → x 0 1 f ( x ) = 0 \lim\limits_{x\to{x_0}}\frac{1}{f(x)}=0 x→x0limf(x)1=0
-
隐去细节的紧凑版本: ∀ ϵ > 0 \forall{\epsilon>0} ∀ϵ>0,对于 M = 1 ϵ M=\frac{1}{\epsilon} M=ϵ1, ∃ δ > 0 \exist{\delta>0} ∃δ>0,当 0 < ∣ x − x 0 ∣ < δ 0<|x-x_0|<\delta 0<∣x−x0∣<δ时, ∣ f ( x ) ∣ > M = 1 ϵ |f(x)|>M=\frac{1}{\epsilon} ∣f(x)∣>M=ϵ1,即 ∣ 1 f ( x ) ∣ < ϵ |\frac{1}{f(x)}|<\epsilon ∣f(x)1∣<ϵ,所以 lim x → x 0 1 f ( x ) = 0 \lim\limits_{x\to{x_0}}\frac{1}{f(x)}=0 x→x0limf(x)1=0
-
反之,设 lim x → x 0 f ( x ) = 0 \lim\limits_{x\to{x_0}}f(x)=0 x→x0limf(x)=0,且 f ( x ) ≠ 0 f(x)\neq{0} f(x)=0
- ∀ M > 0 \forall{M>0} ∀M>0,根据无穷小的定义,对于 ϵ = 1 M \epsilon=\frac{1}{M} ϵ=M1, ∃ δ > 0 \exist{\delta>0} ∃δ>0,当 0 < ∣ x − x 0 ∣ < δ 0<|x-x_0|<\delta 0<∣x−x0∣<δ, ∣ f ( x ) ∣ < ϵ = 1 M |f(x)|<\epsilon=\frac{1}{M} ∣f(x)∣<ϵ=M1
- 由于当 0 < ∣ x − x 0 ∣ < δ 0<|x-x_0|<\delta 0<∣x−x0∣<δ时 f ( x ) ≠ 0 f(x)\neq{0} f(x)=0,从而 ∣ 1 f ( x ) ∣ > M |\frac{1}{f(x)}|>M ∣f(x)1∣>M
- 所以 lim x → x 0 1 f ( x ) = ∞ \lim\limits_{x\to{x_0}}\frac{1}{f(x)}=\infin x→x0limf(x)1=∞
-
无穷小@无穷大的运算法则
- 参见极限的运算法则
相关文章:

AM@无穷小和无穷大
文章目录 abstract本文符号说明无穷小无穷小和自变量变化过程无穷小和函数极限的关系定理👺证明 无穷大无穷大不是数极限无穷大的说法证明函数极限为无穷大 无穷大和无穷小见的关系定理无穷小无穷大的运算法则 abstract 无穷小和无穷大的概念和相关性质 本文符号说…...
玄子Share- IDEA 2023 SpringBoot 热部署
玄子Share- IDEA 2023 SpringBoot 热部署 修改 IDEA 部署设置 IDEA 勾选如下选项 新建 SpringBoot 项目 项目构建慢的将 Spring Initializr 服务器 URL 改为阿里云:https://start.aliyun.com/ 在这里直接勾选Spring Boot Devtools插件即可 测试 切出 IDEA 项目文…...
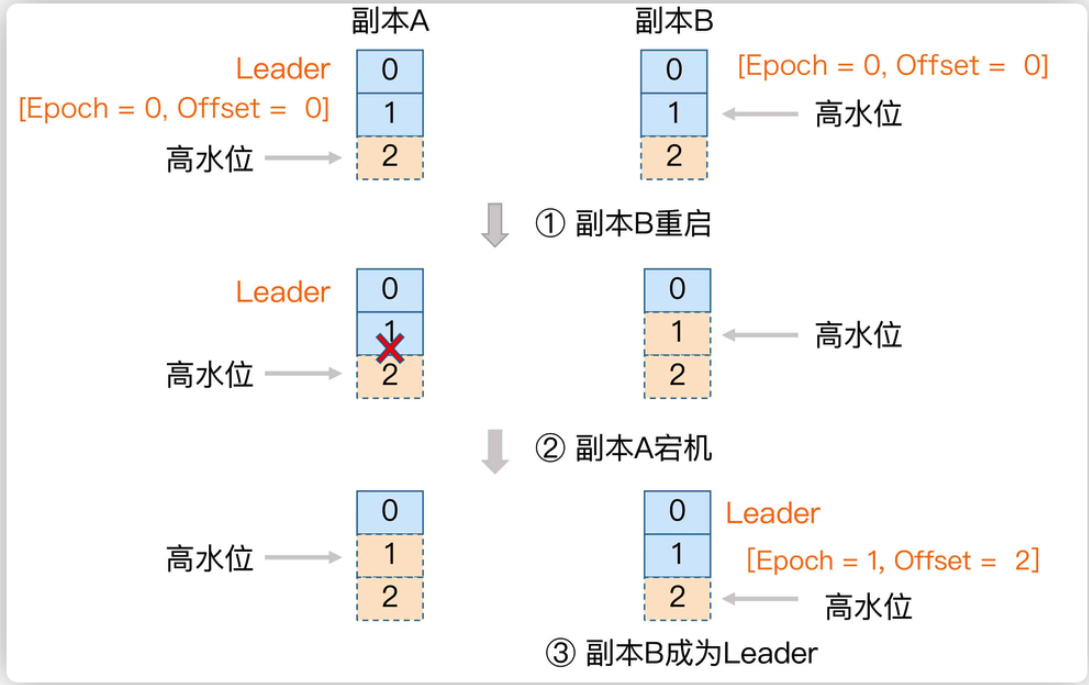
kafka集群工作机制
一、kafka在zookeeper上的元数据解释 kafka中的broker要选举Controller角色来管理整个kafka集群中的分区和副本状态。一个Topic下多个partition要选举Leader角色和客户端进行交互数据 Zookeeper客户端工具: prettyZoo。 下载地址:https://github.com/vr…...
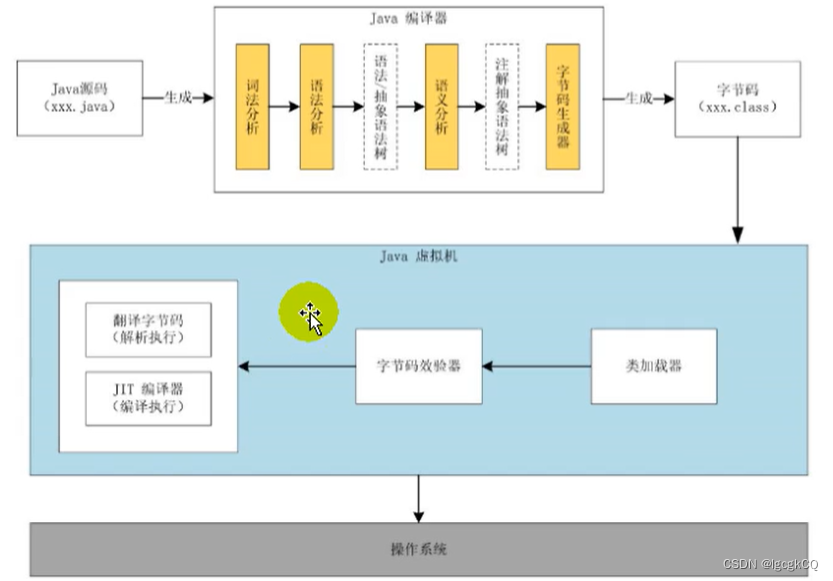
JVM上篇之虚拟机与java虚拟机介绍
目录 虚拟机 java虚拟机 简介 特点 作用 位置 整体结构 类装载子系统 运行时数据区 java执行引擎 Java代码执行流程 jvm架构模型 基于栈式架构 基于寄存器架构 总结 jvm的生命周期 1.启动 2.执行 3.退出 JVM的发展历程 虚拟机 所谓虚拟机,指的…...
在公众号上怎么创建微信付费课程功能呢
微信付费课程功能是一项比较受欢迎的在线教育服务,可以帮助教育机构或个人更好地管理和销售课程资源,提高知识分享和变现的效率。下面将介绍如何创建微信付费课程功能。 一、了解微信付费课程功能 在创建微信付费课程功能之前,需要先了解微信…...
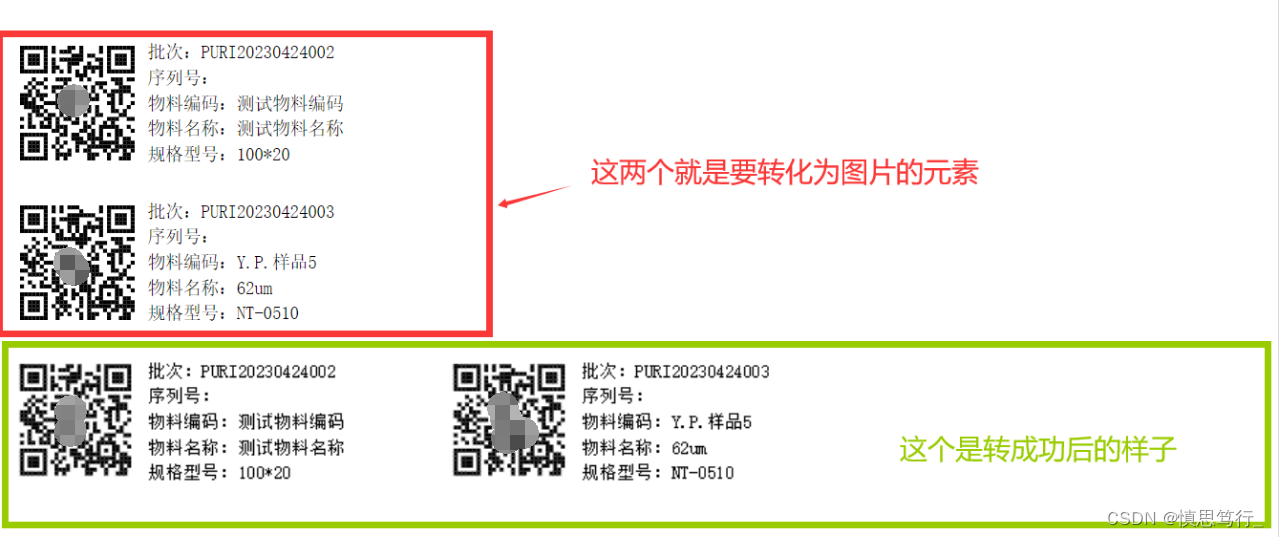
HTML5使用html2canvas转化为图片,然后再转为base64.
介绍 场景:今天同事提了个协助,将HTML5文件中的元素转为图片,并且最终转为base64格式传给后端。感觉还挺有意思就记录下。(试例如下) 步骤一:引入html2canvas 的js源码 html2canvas.min.js 下载地址 htt…...
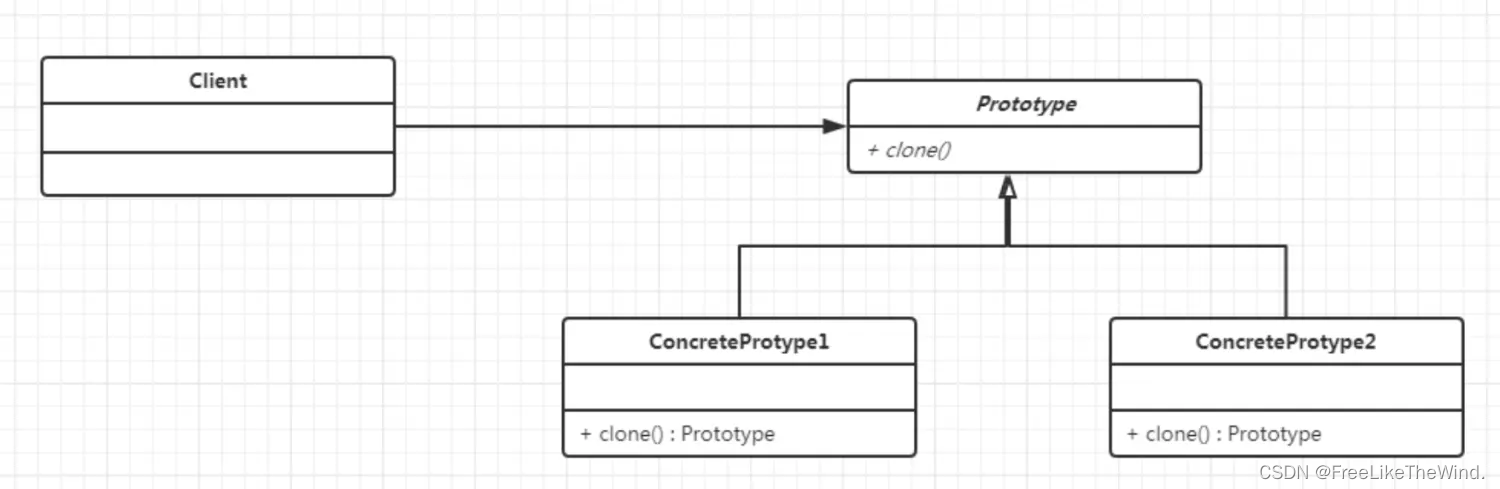
【C++设计模式之原型模式:创建型】分析及示例
简介 原型模式(Prototype Pattern)是一种创建型设计模式,它允许通过复制已有对象来生成新的对象,而无需再次使用构造函数。 描述 原型模式通过复制现有对象来创建新的对象,而无需显式地调用构造函数或暴露对象的创建…...
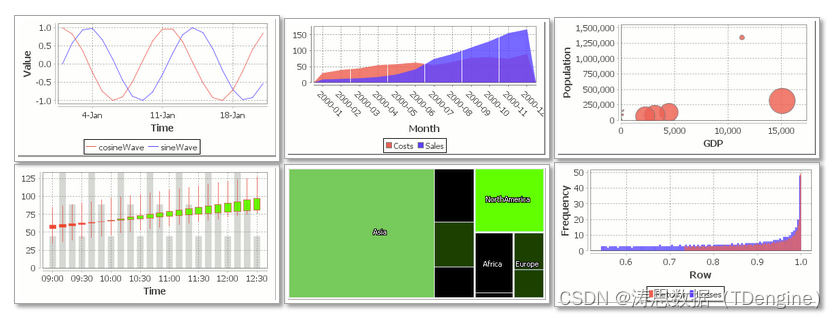
TDengine OSS 与 qStudio 实现无缝协同,革新数据分析和管理方式
在数字化转型如火如荼的当下,海量爆发的时序数据处理成为转型成功的关键因素之一。为了帮助社区用户更好地进行数据分析和管理,丰富可视化解决方案的多样性,我们将开源的时序数据库(Time Series Database) TDengine OS…...

css的gap设置元素之间的间隔
在felx布局中可以使用gap来设置元素之间的间隔; .box{width: 800px;height: auto;border: 1px solid green;display: flex;flex-wrap: wrap;gap: 100px; } .inner{width: 200px;height: 200px;background-color: skyblue; } <div class"box"><…...
Flask-[项目]-搭建短网址系统:flask实现短网址系统,短网址系统,构建短网址系统
一、项目下载地址 https://gitee.com/liuhaizhang/short-url-systemhttps://gitee.com/liuhaizhang/short-url-system 二、项目搭建 2.1、基本环境安装 1、安装好mysql数据库 2、安装好redis数据 3、安装好python解释器 2.2、项目依赖安装 1、切换到python解释器环境中 …...
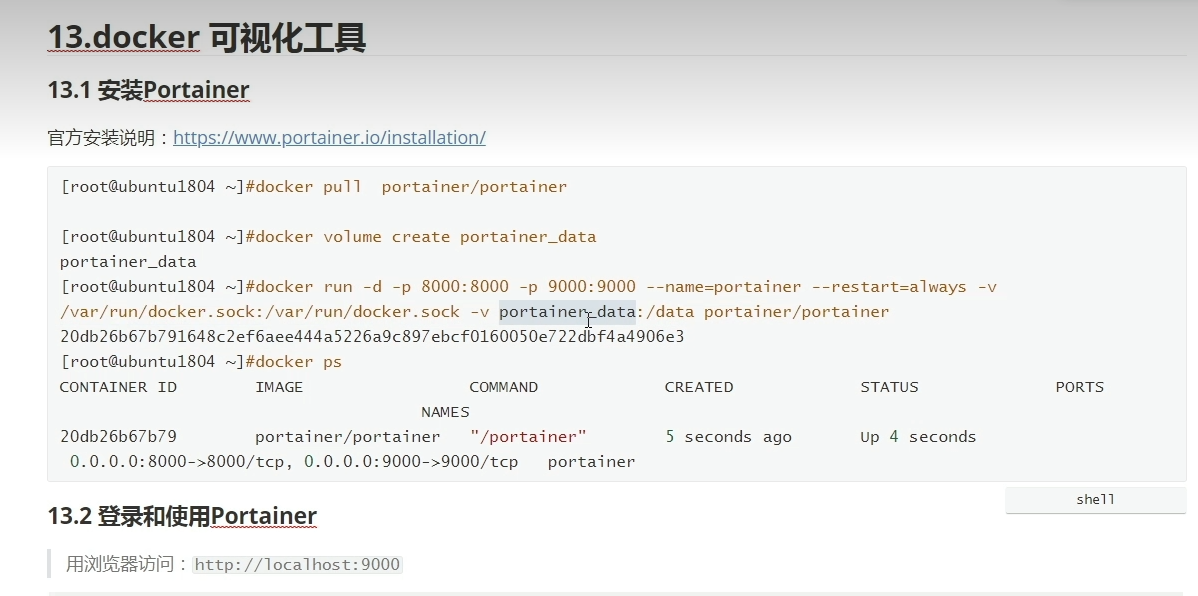
【从0开始配置前后端项目】——Docker环境配置
1. 准备一台纯净的服务器 镜像:CentOS 7.9 64位 CPU & 内存:2核2G 系统盘:60GB 峰值带宽:30Mbps 流量包:600GB / 600GB 2. 安装Docker 2.1 卸载旧的版本 $ sudo yum remove docker \docker-client \docker-cl…...
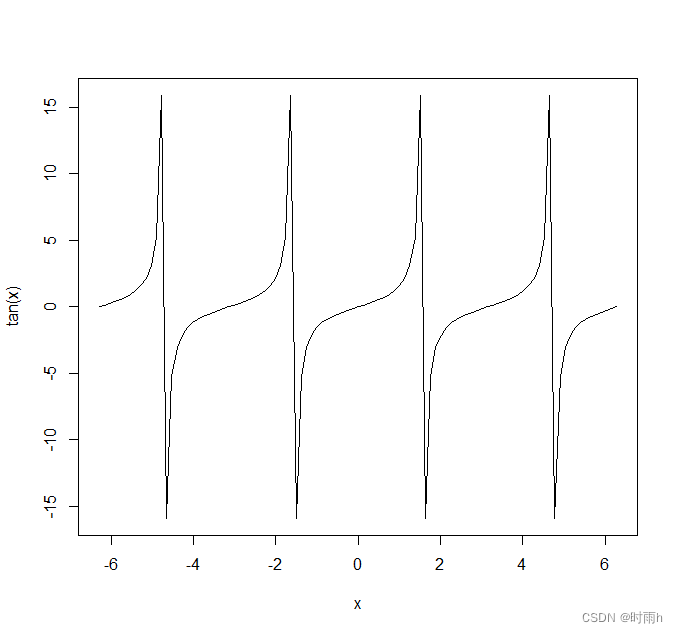
R语言 一种功能强大的数据分析、统计建模 可视化 免费、开源且跨平台 的编程语言
R语言是一种广泛应用于数据分析、统计建模和可视化的编程语言。它由新西兰奥克兰大学的罗斯伊哈卡和罗伯特杰特曼开发,并于1993年首次发布。R语言是一个免费、开源且跨平台的语言,它在统计学和数据科学领域得到了广泛的应用。 R语言具有丰富的数据处理、…...
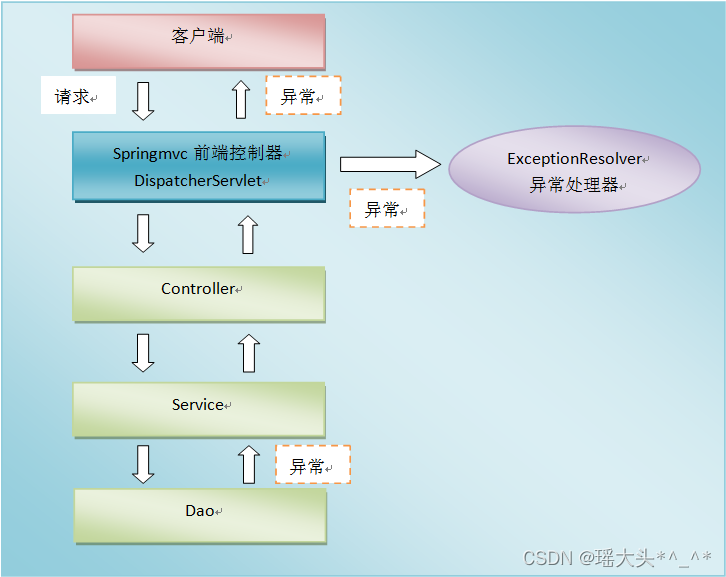
springmvc-JSR303进行服务端校验分组验证SpringMVC定义Restfull接口异常处理流程RestController异常处理
目录& 1. JSR303 2. JSR303中含有的注解 3. spring中使用JSR303进行服务端校验 3.1 导入依赖包 3.2 添加验证规则 3.3 执行校验 4. 分组验证 4.1 定义分组验证规则 4.2 验证时通过参数指定验证规则 4.3 验证信息的显示 5. SpringMVC定义Restfull接口 5.1 增加s…...
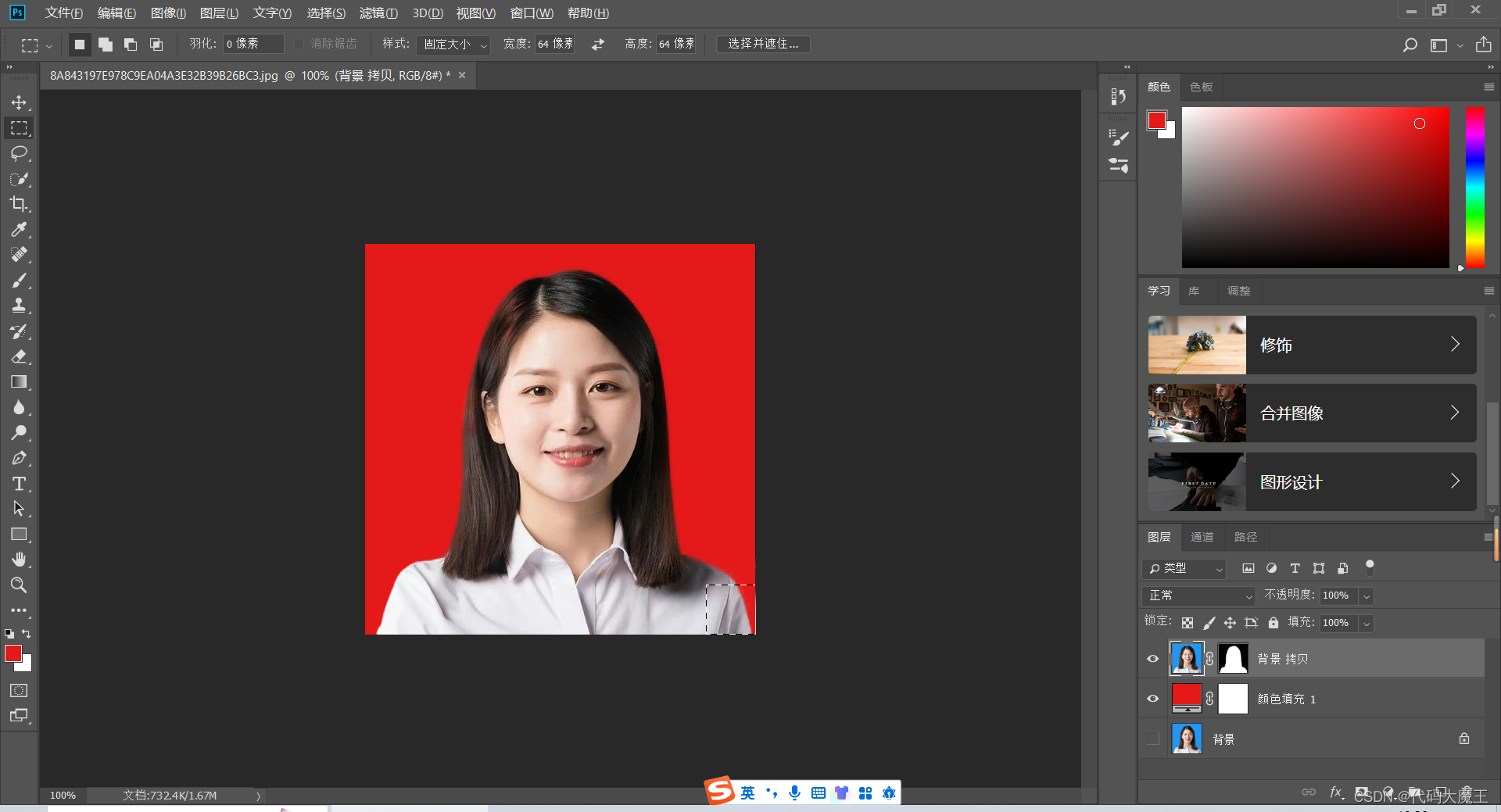
证件照换底色详细教程
说到证件照的底色更改,我想对大部分朋友来说是蛮头疼的事情,由于我们不论是在生活还是学习中,有时候总会要上传一些证件照,而当你手上有证件照准备上传时,发现底色不对,是不是很抓狂,现在&#…...

【ringbuff share mem】
ringbuff 和share mem 结合实现PV操作 参考链接 https://juejin.cn/post/7113550346835722276 https://zhuanlan.zhihu.com/p/147826545 代码如下: #include "rb.h"int g_shmid 0;shm_buff * create_shm(int *smid) {int id;shm_buff *share_mem NU…...
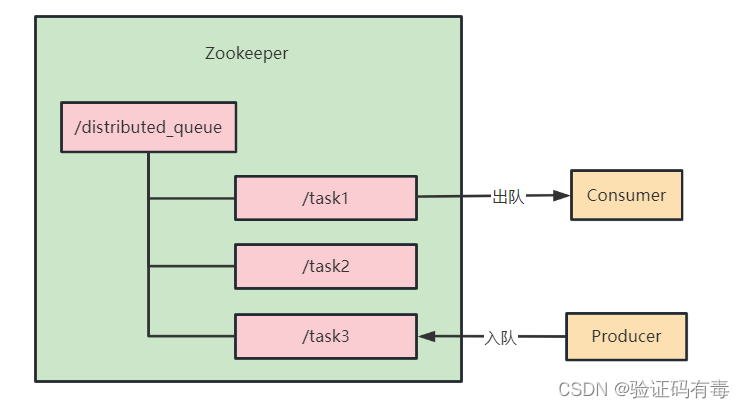
【Zookeeper专题】Zookeeper经典应用场景实战(一)
目录 前置知识课程内容一、Zookeeper Java客户端实战1.1 Zookeeper 原生Java客户端使用1.2 Curator开源客户端使用快速开始使用示例 二、Zookeeper在分布式命名服务中的实战2.1 分布式API目录2.2 分布式节点的命名2.3 分布式的ID生成器 三、zookeeper实现分布式队列3.1 设计思路…...
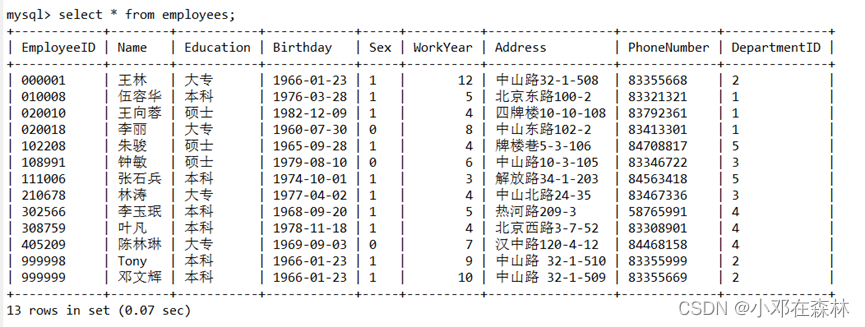
【数据库——MySQL】(15)存储过程、存储函数和事务处理习题及讲解
目录 1. 题目1.1 存储过程1.2 存储函数1.3 事务处理 2. 解答2.1 存储过程2.2 存储函数2.3 事务处理 1. 题目 1.1 存储过程 创建表 RandNumber :字段:id 自增长, data int; 创建存储过程向表中插入指定个数的随机数(1-…...

FFmpeg:打印音/视频信息(Meta信息)
多媒体文件基本概念 多媒体文件其实是个容器在容器里面有很多流(Stream/Track)每种流是由不同的编码器编码的从流中读出的数据称为包在一个包中包含着一个或多个帧 几个重要的结构体 AVFormatContextAVStreamAVPacket FFmpeg操作流数据的基本步骤 打印音/视频信息(Meta信息…...

1.Linux入门基本指令
个人主页:Lei宝啊 愿所有美好如期而遇 目录 01.ls指令 02.pwd指令 03.cd指令 04.touch指令 05.mkdir指令(重要) 06.rmdir&&rm指令(重要) 07.man指令(重要) 08.cp指令(重要) 09.mv指令(重要) 10.cat指令 nano指令 echo指令 输出重定向 追加重…...
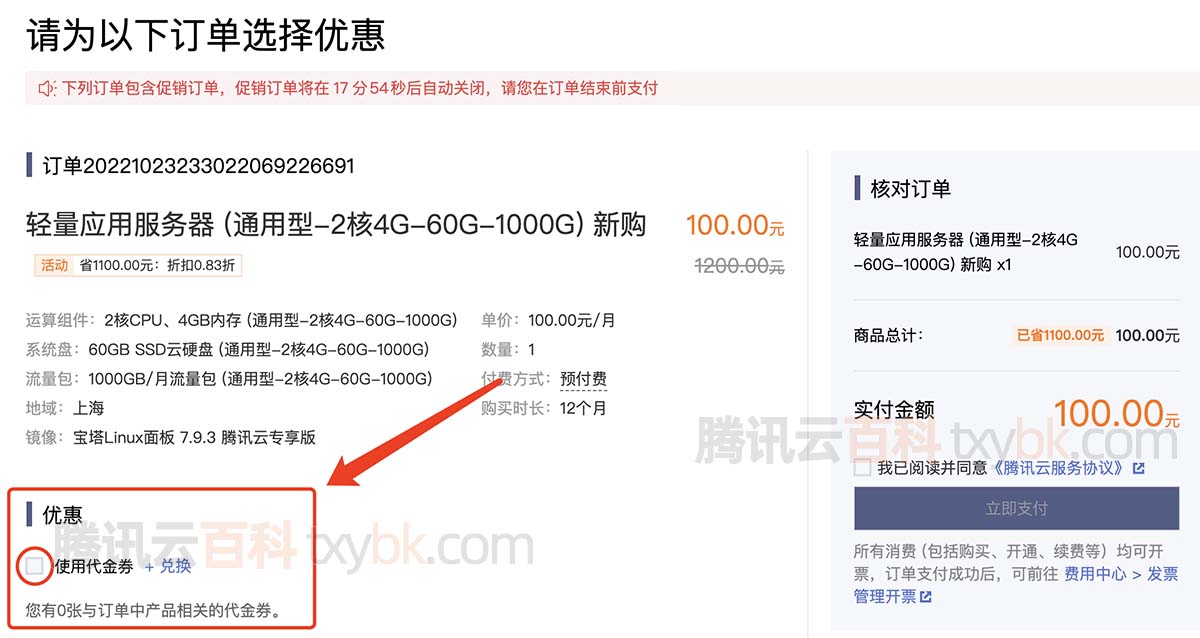
2023腾讯云服务器优惠代金券领取、查询及使用说明
腾讯云代金券领取渠道有哪些?腾讯云官网可以领取、官方媒体账号可以领取代金券、完成任务可以领取代金券,大家也可以在腾讯云百科蹲守代金券,因为腾讯云代金券领取渠道比较分散,腾讯云百科txybk.com专注汇总优惠代金券领取页面&am…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
