JAVA练习百题之求矩阵对角线之和
题目:求一个3*3矩阵对角线元素之和
程序分析
求一个3x3矩阵的对角线元素之和,我们需要将矩阵的左上到右下以及左下到右上两条对角线上的元素相加。
一个3x3矩阵如下所示:
1 2 3
4 5 6
7 8 9
左上到右下的对角线元素和为1 + 5 + 9 = 15,左下到右上的对角线元素和为7 + 5 + 3 = 15。
下面我们将使用三种不同的方法来实现这个任务,并分析它们的优缺点。
方法一:使用嵌套循环遍历矩阵
解题思路
我们可以使用嵌套循环遍历矩阵的元素,将左上到右下和左下到右上两条对角线上的元素相加。
实现代码
public class Main {public static void main(String[] args) {int[][] matrix = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};int sum1 = 0, sum2 = 0;for (int i = 0; i < matrix.length; i++) {sum1 += matrix[i][i]; // 左上到右下的对角线sum2 += matrix[i][matrix.length - 1 - i]; // 左下到右上的对角线}System.out.println("Sum of diagonal elements (left to right): " + sum1);System.out.println("Sum of diagonal elements (right to left): " + sum2);}
}
优缺点
优点:
- 简单易懂,容易实现。
- 对于小规模矩阵,性能良好。
缺点:
- 随着矩阵大小的增加,性能可能下降,时间复杂度为O(n)。
方法二:直接计算
解题思路
我们可以直接计算对角线元素之和,而不需要遍历整个矩阵。对于一个3x3矩阵,左上到右下的对角线元素之和为matrix[0][0] + matrix[1][1] + matrix[2][2],左下到右上的对角线元素之和为matrix[2][0] + matrix[1][1] + matrix[0][2]。
实现代码
public class Main {public static void main(String[] args) {int[][] matrix = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};int sum1 = matrix[0][0] + matrix[1][1] + matrix[2][2]; // 左上到右下的对角线int sum2 = matrix[2][0] + matrix[1][1] + matrix[0][2]; // 左下到右上的对角线System.out.println("Sum of diagonal elements (left to right): " + sum1);System.out.println("Sum of diagonal elements (right to left): " + sum2);}
}
优缺点
优点:
- 直接计算,不需要遍历整个矩阵,性能较好。
- 对于小规模矩阵,性能良好。
缺点:
- 对于大规模矩阵,时间复杂度仍然为O(1),没有显著的性能提升。
方法三:使用循环
解题思路
我们可以使用循环来计算对角线元素之和,避免直接硬编码每个元素的位置。
实现代码
public class Main {public static void main(String[] args) {int[][] matrix = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};int sum1 = 0, sum2 = 0;for (int i = 0; i < matrix.length; i++) {sum1 += matrix[i][i]; // 左上到右下的对角线sum2 += matrix[i][matrix.length - 1 - i]; // 左下到右上的对角线}System.out.println("Sum of diagonal elements (left to right): " + sum1);System.out.println("Sum of diagonal elements (right to left): " + sum2);}
}
优缺点
优点:
- 使用循环计算,不需要硬编码每个元素的位置,具有一定的灵活性。
- 对于小规模矩阵,性能良好。
缺点:
- 对于大规模矩阵,时间复杂度仍然为O(n)。
总结
对于小规模矩阵,三种方法的性能都较好,且实现都相对简单。方法一和方法三具有一定的灵活性,可以用于不同大小的矩阵,但时间复杂度为O(n)。方法二直接计算,性能也较好,但不具备灵活性。
综合考虑,如果只处理小规模矩阵,方法一或方法三都可以选择,取决于个人喜好。如果需要处理大规模矩阵,方法二是一个更好的选择,因为它的时间复杂度是常数级的,不受矩阵大小的影响。
相关文章:

JAVA练习百题之求矩阵对角线之和
题目:求一个3*3矩阵对角线元素之和 程序分析 求一个3x3矩阵的对角线元素之和,我们需要将矩阵的左上到右下以及左下到右上两条对角线上的元素相加。 一个3x3矩阵如下所示: 1 2 3 4 5 6 7 8 9左上到右下的对角线元素和为1 5 9 15&…...

MEM备考打卡
今天是2023.10.9距离考试还有75天 三年前就想考MEM每次总是有各种原因最后选择了放弃,没时间、自制力差、害怕失败。。。。放弃后确还是会想如果自己当时没有放弃是不是就能考上,所以这次不管能不能考上拼搏75天,不能总是停留在想象。加油&a…...

短视频矩阵源码开发部署---技术解析
一、短视频SEO源码搜索技术需要考虑以下几点: 1. 关键词优化:通过研究目标受众的搜索习惯,选择合适的关键词,并在标题、描述、标签等元素中进行优化,提高视频的搜索排名。 2. 内容质量:优质、有吸引力的内…...

百度小程序制作源码 百度引流做关键词排名之技巧
百度作为国内最大的搜索引擎,对于关键词排名和流量获取的策略格外重要,下面给大家分享一个百度小程序制作源码和做百度引流、关键词排名的一些技巧。 移动设备的普及和微信小程序的火热,百度也推出了自己的小程序。百度小程序与微信小程序类…...

【计算机组成 课程笔记】7.3 高速缓存 Cache
课程链接: 计算机组成_北京大学_中国大学MOOC(慕课) 7 - 5 - 705-高速缓存的工作原理(16-00--)_哔哩哔哩_bilibili 在【计算机组成 课程笔记】7.1 存储层次结构概况_Elaine_Bao的博客-CSDN博客中提到,因为CPU和内存的速度差距越来…...

vscode搭建c/c++环境
1. 安装mingw64 2.vscode安装c/c插件,run插件 3.在workspace/.vscode文件夹下新建三个文件: 1)c_cpp_properties.json { "configurations": [ { "name": "Win32", "includePath": [ "${wor…...
 正式版带 OpenCore 0.9.6 和 FirPE 三分区镜像)
macOS Sonoma 14.0(23A344) 正式版带 OpenCore 0.9.6 和 FirPE 三分区镜像
macOS Sonoma 14.0(23A344) 正式版官方镜像百度网盘 请输入提取码 https://www.aliyundrive.com/s/sMUUedQdoiu 提取码 71dzmacOS Sonoma 14.0(23A344) 正式版带 OpenCore 0.9.6 和 FirPE 引导百度网盘 请输入提取码 https://www.123pan.com/s/o6d9-BdMX.html 提取码 5Pc2macO…...
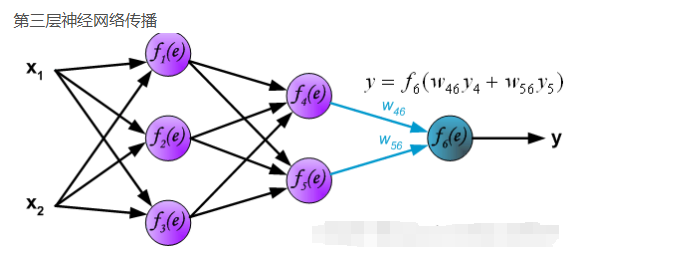
神经网络(MLP多层感知器)
分类 神经网络可以分为多种不同的类型,下面列举一些常见的神经网络类型: 前馈神经网络(Feedforward Neural Network):前馈神经网络是最基本的神经网络类型,也是深度学习中最常见的神经网络类型。它由若干个…...

git与github的交互(文件与文件夹的上传)
git与github的交互(文件与文件夹的上传) 准备:gitHub账号(创建一个新项目)与Git软件的安装 一:开启公钥SSH登录(之前配置过就跳过) 1.安装SSH 在本地新创建文件夹负责装载项目&a…...

Visual Studio常见编译错误记录
错误1:错误(活动)E0020未定义标识符 “sleep” sleep(3000); //将小写sleep改为 Sleep Sleep(3000);错误2:错误 C4996 ‘fopen’: This function or variable may be unsafe. Consider using fopen_s instead. To disable deprecation, use _CRT_SECURE…...

如何应对数据安全四大挑战?亚马逊云科技打出“组合拳”
数字经济时代,数据被公认为继土地、劳动力、资本、 技术之后的又一重要生产要素。对于企业而言,数据则是一切创新与关键决策的根源。 然而,企业在发挥数据资产的商业价值方面,却面临诸多挑战,比如敏感数据识别、跨组织…...
JavaScript——数据类型、类型转换
数据类型 计算机世界中的万事万物都是数据。 计算机程序可以处理大量的数据,为什么要给数据分类? 更加充分和高效的利用内存也更加方便程序员的使用数据 基本数据类型 number 数字型 JavaScript中正数、负数、小数等统一称为number JS是弱数据类型࿰…...
C位操作符
目录 一、位操作符 1.位与& 2.位或| 3.位取反~ 4.位异或^ 5.位与,位或,位异或的特点总结 6.左移位《《 右移位 》》 二、位与,位或,位异或在操作寄存器时的特殊作用 1.寄存器操作的要求(特定位改变而不…...

【linux进程(三)】进程有哪些状态?--Linux下常见的三种进程状态
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:Linux从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学更多操作系统知识 🔝🔝 Linux进程 1. 前言2. 操作系统…...
 - ‘0‘)
numString.charAt(i) - ‘0‘
numString.charAt(i) 表示获取字符串 numString 中第 i 个字符,这里假设该字符是数字 0 到 9 之间的一个字符。 0 是字符常量,表示数字 0 对应的字符。例如,字符 0 转换成数字就是 0,字符 1 转换成数字就是 1,以此类推…...

《Python 自动化办公应用大全》书籍推荐(包邮送书五本)
前言 随着科技的快速发展和智能化办公的需求增加,Python自动化办公成为了一种趋势。Python作为一种高级编程语言,具有简单易学、功能强大和开放源代码等优势,可以帮助我们更高效地完成日常办公任务。 Python自动化办公还可以帮助我们实现更…...

day57:ARMday4,程序状态寄存器读写指令、软中断指令、C和汇编的混合编程、开发板介绍
思维导图:有道云笔记...

el-cascader
场景: el-cascader lazy multiple 反显数据 非lazy的场景 selecetedOptions2: [[1, 2, 3],[1, 2, 4], ],可以正常回显;> ok lazy场景下: 是不可以回显的… 如果el-cascader是异步的单选 cascader默认会加载下个层级的(子…...

图论第3天----第841题、第463题
# 图论第3天----第841题、第463题 文章目录 一、第841题--钥匙和房间二、第463题--岛屿的周长 又继续开始修行,把图论这块补上,估计要个5-6天时间。 一、第841题–钥匙和房间 有向图的遍历。dfs遍历3部曲做,思路也较顺----访问过的&a…...

软件测试/测试开发丨利用ChatGPT 生成自动化测试脚本
点此获取更多相关资料 简介 自动化测试脚本可以模拟用户与应用程序的交互,例如点击按钮、输入数据、导航到不同的页面等等,以验证应用程序的正确性、性能和稳定性。 自动化测试在回归测试、冒烟测试等测试流程中都可以极大地起到节省时间、节省人力的作…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...
