图论---最小生成树问题
在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。解决最小生成树问题一般有两种算法:Kruskal算法和Prim算法。
Kruskal算法
原理:基本思想是从小到大加入边,是个贪心算法。我们将图中的每个边按照权重大小进行排序,每次从边集中取出权重最小且两个顶点都不在同一个集合的边加入生成树中。注意:如果这两个顶点都在同一集合内,说明已经通过其他边相连,因此如果将这个边添加到生成树中,那么就会形成环。这样反复做,直到选出n-1条边。时间复杂度为O(m*logm)
算法过程:此算法可以称为“加边法”,初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。 具体过程如下所示: 步骤1:先对图中所有的边按照权值进行排序 步骤2:如果当前这条边的两个顶点不在一个集合里面,那么就用并查集的Union函数把他们合并在一个集合里面(也就是把他们放在最小生成树里面),如果在一个并查集里面,我们就舍弃这条边,不需要这条边。 步骤3:一直执行步骤2,知道当边数等于n-1(n为节点个数),那就说明这n个顶点就连合并在一个集合里面了;如果边数不等于顶点数目减去1,那么说明这些边就不连通,即无法构成最小生成树。
代码框架:
int n, m; // n是点数,m是边数
int p[n + 1]; // 并查集的父节点数组
struct Edge{ // 存储边 int a, b, w; bool operator< (const Edge &W)const { return w < W.w; }
}edges[m];
int find(int x){ // 并查集核心操作 return p[x] == x ? x : p[x] = find(p[x]);
}
void init(){ // 初始化并查集 for(int i = 1; i <= n; i++){p[i] = i;}
}
int kruskal() {sort(edges, edges + m); init();int res = 0, cnt = 0; for (int i = 0; i < m; i++) { // 从m条边选择n-1条边int a = edges[i].a, b = edges[i].b, w = edges[i].w; a = find(a), b = find(b); if (a != b) { // 如果两个连通块不连通,则将这两个连通块合并p[a] = b; res += w; cnt++; } }if (cnt < n - 1) return INF; return res;
}
Prim算法
原理:基本思想是从一个结点开始,不断加点。因此该算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。时间复杂度为O(n * n + m)。
算法过程:
-
用两个集合A{},B{}分别表示找到的点集,和未找到的点集;
-
我们以A中的点为起点a,在B中找一个点为终点b,这两个点构成的边(a,b)的权值是其余边中最小的
-
重复上述步骤#2,直至B中的点集为空,A中的点集为满
代码框架:
int n; // 节点个数
vector<vector<int>> g(n, vector<int>(n)); // 邻接矩阵,存储所有边
vector<int> dis(n); // 存储其他节点到当前最小生成树的距离
vector<bool> v(n); // 存储每个节点是否加入到最小生成树中
// 如果图不连通,则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim(){const int inf = 0x3f3f3f3f;memset(dis, 0x3f, sizeof dis);int res = 0;for(int i = 0; i < n; i++){int p = -1;for(int j = 0; j < n; j++){if(!v[j] && (p == -1 || dis[j] < dis[p])){p = j;}}if(i && dis[p] == inf){ // dis[p] = inf说明找到的节点与最小生成树不连通,但是当i = 0说明是第一个节点,不考虑连通return inf;}if(i){res += dis[p];}v[p] = true;for(int j = 0; j < n; j++){dis[j] = min(dis[j], g[p][j]); // 与Dijkstra算法的区别}}return res;
}
题单
1584. 连接所有点的最小费用 - 力扣(LeetCode)
相关文章:

图论---最小生成树问题
在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。解决最小生成树问题一般有两种算法:Kruskal算法和Prim算法。 Kruskal算法 原理:基本思想是从小到大加入边,是个贪心算法。我们将图中的每个边按…...

elementplus 时间范围选择器限制选择时间范围
<el-date-pickerv-model"form.time" type"daterange"range-separator"-"start-placeholder"开始时间"end-placeholder"结束":disabled-date"disabledDate"calendar-Change"calendarChange" />co…...
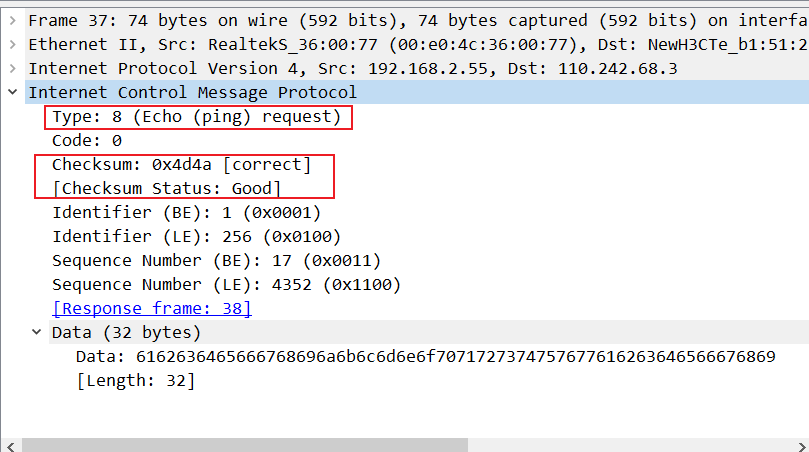
【网络】抓包工具Wireshark下载安装和基本使用教程
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_Linux,大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的帮助…...

Metasequoia 4 水杉3D建模工具 附序列号
Metasequoia 4是一款非常强大的3D水杉建模工具,它基于多边形建模技术,可以用于创建各种对象并支持多种第三方3DCG软件的文件格式,是一款非常适合从爱好到业务,支持3D电脑绘图,3D印刷,游戏开发等的3D建模软件…...

股票杠杆交易平台排名:淘配网推荐的十大平台
在投资世界中,股票杠杆交易一直以其提供更高回报机会的吸引力而备受欢迎。随着市场的不断发展,出现了越来越多的股票杠杆交易平台。本文将为您介绍淘配网推荐的十大股票杠杆交易平台,并分析它们的特点。 富灯网 - 富灯网以其全面的杠杆产品和…...

CoreData + CloudKit 在初始化 Schema 时报错 A Core Data error occurred 的解决
问题现象 如果希望为 CoreData 支持的 App 增加云数据备份和同步功能,那么 CloudKit 是绝佳的选择。CloudKit 会帮我们默默处理好一切,我们基本不用为升级而操心。 不过,有时在用本地 CoreData NSManagedObjectModel 初始化 iCloud 中的 Schema 时会发生如下错误: Error …...
修炼k8s+flink+hdfs+dlink(三:安装dlink)
一:mysql初始化。 mysql -uroot -p123456 create database dinky; grant all privileges on dinky.* to dinky% identified by dinky with grant option; flush privileges;二:上传dinky。 上传至目录/opt/app/dlink tar -zxvf dlink-release-0.7.4.t…...
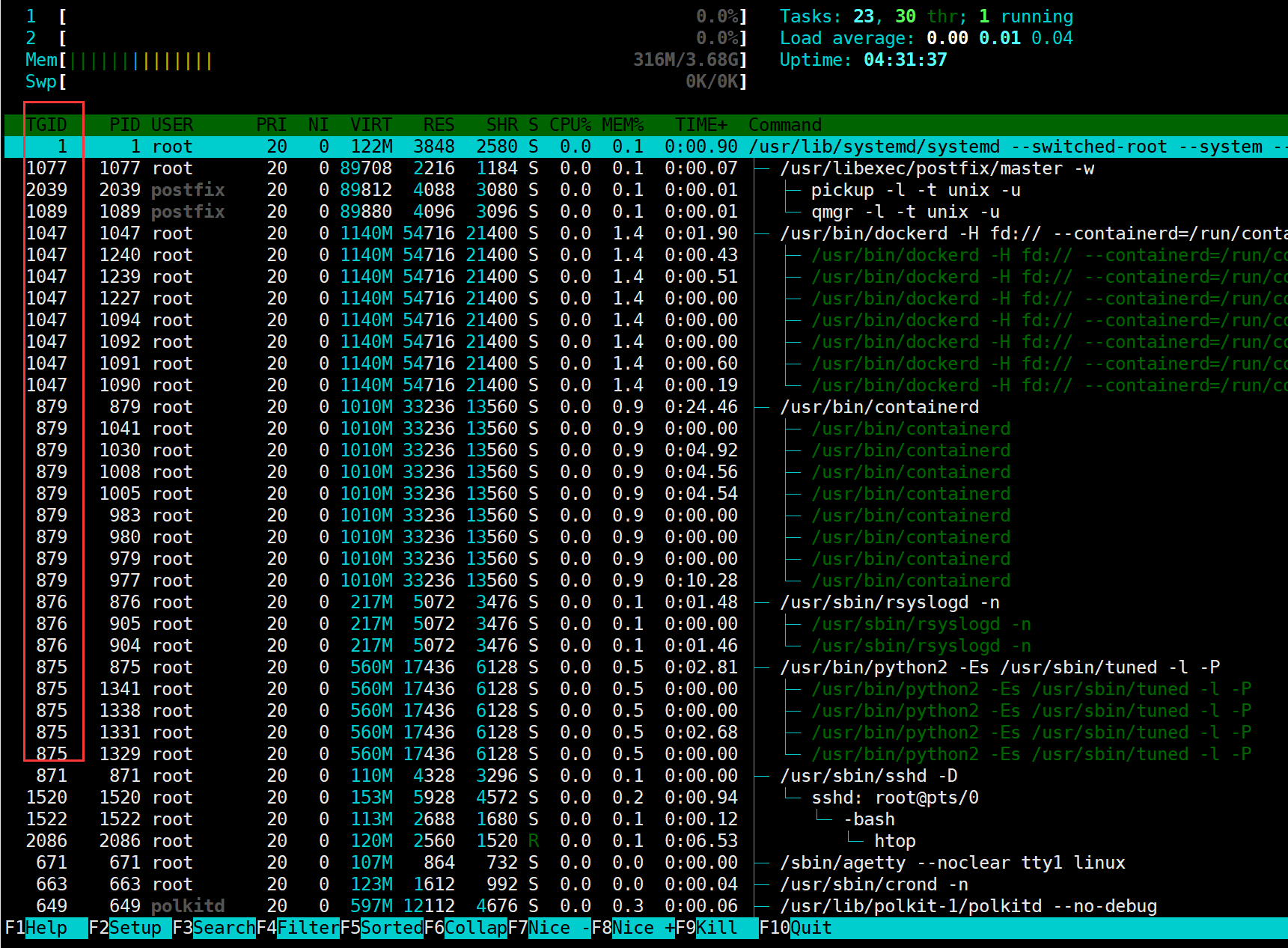
Linux 系统性能瓶颈分析(超详细)
Author:rab 目录 前言一、性能指标1.1 进程1.1.1 进程定义1.1.2 进程状态1.1.3 进程优先级1.1.4 进程与程序间的关系1.1.5 进程与进程间的关系1.1.6 进程与线程的关系 1.2 内存1.2.1 物理内存与虚拟内存1.2.2 页高速缓存与页写回机制1.2.3 Swap Space 1.3 文件系统1…...
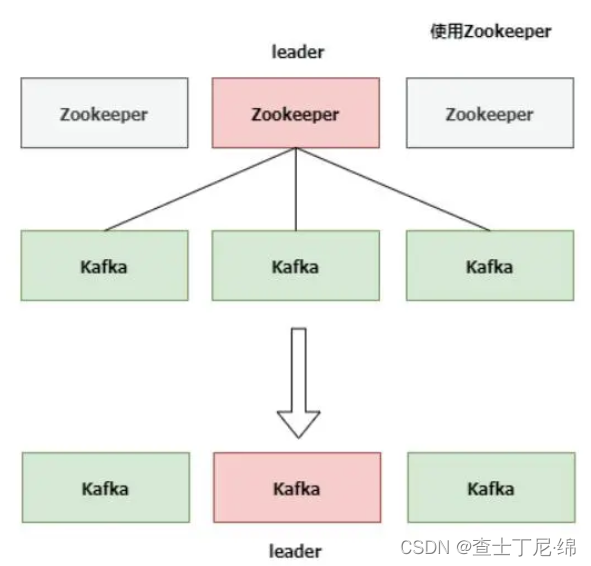
kafka与zookeeper的集群
基础配置 systemctl stop firewalld && systemctl disable firewalld setenforce 0 sed -i s/SELINUXenforcing/SELINUXdisabled/ /etc/selinux/configvi /etc/hosts ip1 node1 ip2 node2 ip3 node3zookeeper介绍 zookeeper是一个分布式的协调服务,主要用…...
sqlalchemy 连接池
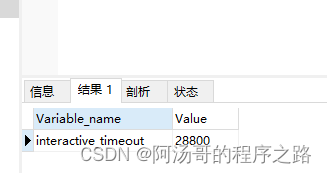
报错 sqlalchemy.exc.TimeoutError: QueuePool limit of size 100 overflow 10 reached, connection timed out, timeout 30 (Background on this error at: http://sqlalche.me/e/3o7r) 查看数据库未活动超时时间 show variables like "interactive_timeout";一般…...
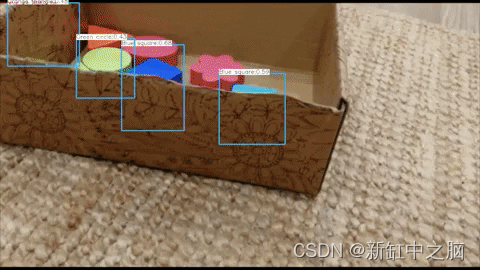
用Blender制作YOLO目标检测器训练数据
推荐:用 NSDT编辑器 快速搭建可编程3D场景 本文将介绍一种非常有吸引力的机器学习训练数据的替代方案,用于为给定的特定应用程序收集数据。 无论应用程序类型如何,这篇博文都旨在向读者展示使用 Blender 等开源资源生成合成数据(S…...
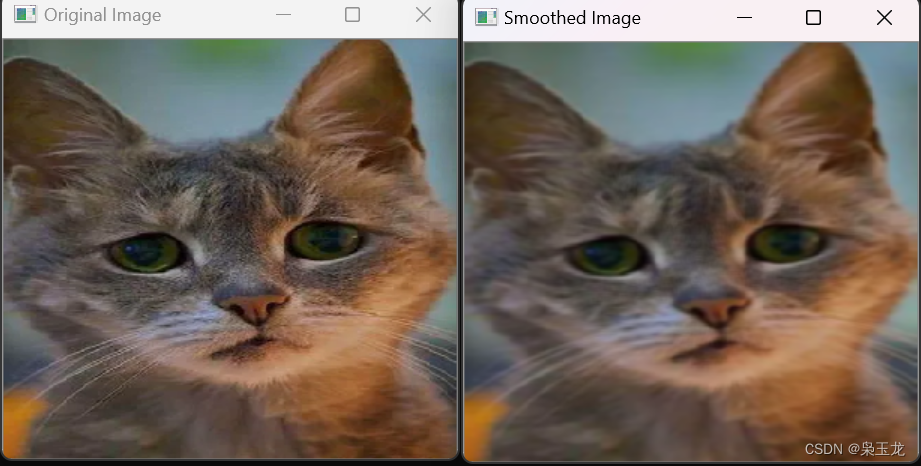
c++视觉处理---均值滤波
均值滤波 cv::blur()函数是OpenCV中用于应用均值滤波的函数。均值滤波是一种简单的平滑技术,它计算每个像素周围像素的平均值,并用该平均值替代原始像素值。这有助于降低图像中的噪声,并可以模糊图像的细节。 以下是cv::blur()函数的基本用…...

QT基础入门——Qt事件(五)
前言: 事件(event)是由系统或者 Qt 本身在不同的时刻发出的。当用户按下鼠标、敲下键盘,或者是窗口需要重新绘制的时候,都会发出一个相应的事件。一些事件在对用户操作做出响应时发出,如键盘事件等&#x…...

自学黑客方法-----(网络安全)
如果你想自学网络安全,首先你必须了解什么是网络安全!,什么是黑客!! 1.无论网络、Web、移动、桌面、云等哪个领域,都有攻与防两面性,例如 Web 安全技术,既有 Web 渗透2.也有 Web 防…...
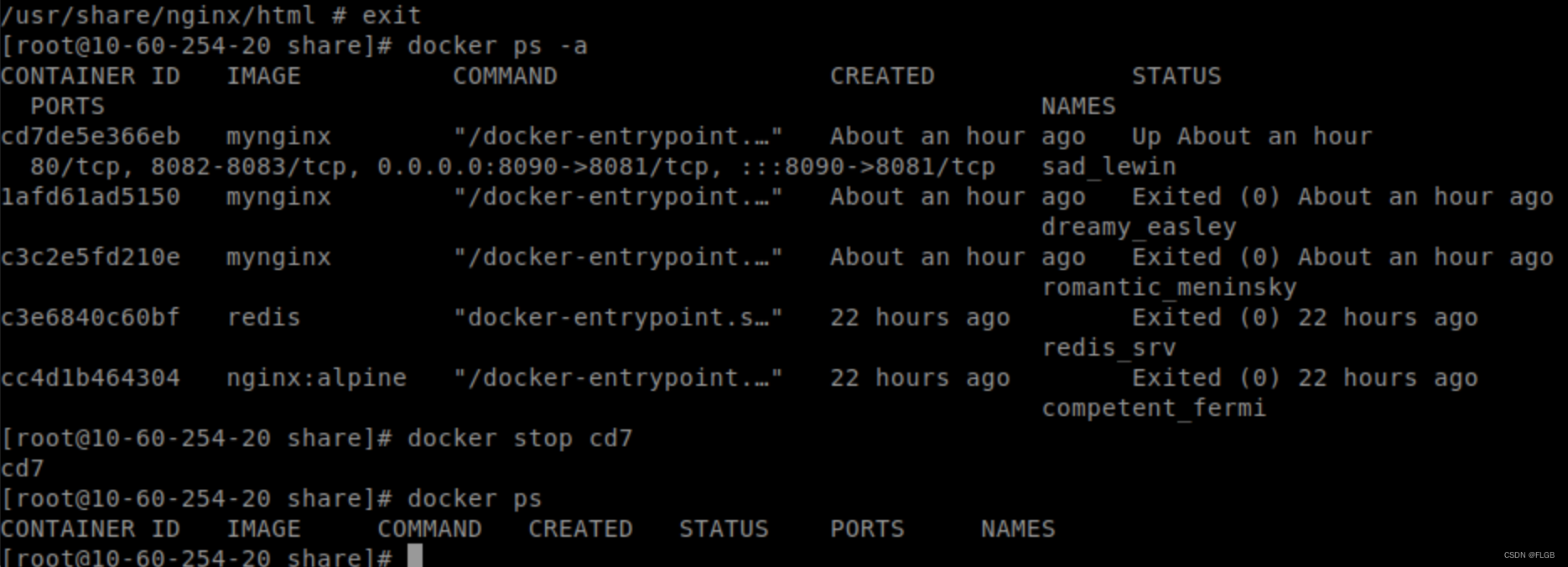
Dockerfile自定义容器
1、Dockerfile Dockerfile 是用于构建 Docker 镜像的文本文件,其中包含一系列的指令和配置,用于定义镜像的构建过程。通过 Dockerfile,你可以定义镜像的基础操作系统、依赖、环境设置、应用程序等信息,从而实现可复制、自动化的镜…...

(5)SpringMVC处理携带JSON格式(“key“:value)请求数据的Ajax请求
SpringMVC处理Ajax 参考文章数据交换的常见格式,如JSON格式和XML格式 请求参数的携带方式 浏览器发送到服务器的请求参数有namevalue&...(键值对)和{key:value,...}(json对象)两种格式 URL请求会将请求参数以键值对的格式拼接到请求地址后面,form表单的GET和POST请求会…...

【iOS】——仿写计算器
文章目录 一、实现思路二、实现方法三、判错处理 一、实现思路 先搭建好MVC框架,接着在各个模块中实现各自的任务。首先要创建好UI界面,接着根据UI界面的元素来与数据进行互动,其中创建UI界面需要用到Masonry布局。 二、实现方法 在calcu…...

公安机关警务vr综合实战模拟训练提高团队合作能力
公安出警VR虚拟仿真培训软件是VR公司利用VR虚拟现实和web3d开发技术,对警务执法过程中可能发生的各种场景进行还原、模拟、演练,结合数据分析,实施量化考核,提高学员的心理承压、应急处突、遇袭反应和临危处置综合能力。 公安出警…...
MySQL-1(12000字详解)
一:数据库的引入 数据库在我们以后工作中是一个非常常用的知识,数据库用来存储数据,但是有些同学可能就会疑惑了,存储数据用文件就可以了,为什么还要弄个数据库呢? 文件保存数据有以下几个缺点࿱…...

voc数据集格式与yolo数据集格式的区别及相互转化
Pascal VOC数据集是目标检测领域最常用的标准数据集之一,几乎所有检测方向的论文都会给出其在VOC数据集上训练并评测的效果。VOC数据集包含的信息非常全,它不仅被拿来做目标检测,也可以拿来做分割等任务,因此除了目标检测所需的文…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
