FP-Growth算法全解析:理论基础与实战指导
目录
- 一、简介
- 什么是频繁项集?
- 什么是关联规则挖掘?
- FP-Growth算法与传统方法的对比
- Apriori算法
- Eclat算法
- FP树:心脏部分
- 二、算法原理
- FP树的结构
- 构建FP树
- 第一步:扫描数据库并排序
- 第二步:构建树
- 挖掘频繁项集
- 优化:条件FP树
- 三、优缺点比较
- 优点
- 1. 效率
- 2. 内存利用
- 3. 可扩展性
- 缺点
- 1. 初始化成本
- 2. 不适用于所有数据类型
- 3. 参数敏感性
- 四、算法实战
- 问题描述
- 环境准备
- Python实现
- 五、总结
本篇博客全面探讨了FP-Growth算法,从基础原理到实际应用和代码实现。我们深入剖析了该算法的优缺点,并通过Python示例展示了如何进行频繁项集挖掘。
关注TechLead,分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验,同济本复旦硕,复旦机器人智能实验室成员,阿里云认证的资深架构师,项目管理专业人士,上亿营收AI产品研发负责人。

一、简介
FP-Growth(Frequent Pattern Growth,频繁模式增长)算法是一种用于数据挖掘中频繁项集发现的有效方法。它是由Jian Pei,Jiawei Han和Runying Mao在2000年的论文中首次提出的。该算法主要应用于事务数据分析、关联规则挖掘以及数据挖掘领域的其他相关应用。
什么是频繁项集?
频繁项集 是一个包含在多个事务中频繁出现的项(或物品)集合。例如,在购物篮分析中,「牛奶」和「面包」经常一起购买,因此{‘牛奶’, ‘面包’}就是一个频繁项集。
什么是关联规则挖掘?
关联规则挖掘 是一种在大量事务数据中找出有趣关系或模式的方法。这种“有趣的关系”通常是指项之间的关联或者条件依赖关系。例如,在销售数据中,购买了“电视”通常也会购买“遥控器”,形成如下关联规则:“电视 -> 遥控器”。
FP-Growth算法与传统方法的对比
与先前的算法(如Apriori和Eclat)相比,FP-Growth算法提供了更高的效率和速度。它通过两次扫描数据库和建立一个称为“FP树(Frequent Pattern Tree)”的紧凑数据结构,避免了产生大量的候选项集。
Apriori算法
Apriori算法 通常需要多次扫描整个数据库以找出频繁项集,这在大数据集上非常耗时。例如,在一个包含百万条事务记录的数据库中,Apriori可能需要数十次甚至上百次的扫描。
Eclat算法
Eclat算法 采用深度优先搜索策略来找出所有的频繁项集,但没有使用紧凑的数据结构来存储信息。因此,当数据集非常大时,它的内存消耗会变得非常高。例如,在处理包含数百个项目和数万个事务的数据集时,Eclat可能会耗尽所有可用的内存。
FP树:心脏部分
FP树 是FP-Growth算法的核心,是一种用于存储频繁项集的紧凑数据结构。与其他数据结构相比,FP树能更有效地存储和检索信息。例如,如果我们有一个购物记录数据库,其中包括了{‘牛奶’, ‘面包’, ‘黄油’},{‘面包’, ‘苹果’},{‘牛奶’, ‘面包’, ‘啤酒’}等多个事务,FP树将以更紧凑的形式存储这些信息。
二、算法原理
FP-Growth算法的核心思想是使用一种叫做“FP树(Frequent Pattern Tree)”的紧凑数据结构来存储频繁项集信息。这个数据结构能够大大减少需要遍历的搜索空间,从而提高算法的执行效率。
FP树的结构
FP树是一种特殊类型的树形数据结构,用于存储一组事务数据库的压缩版本。树中每一个节点表示一个项(如“牛奶”或“面包”),同时存储该项在数据库中出现的次数。
例如,考虑下面的事务数据集:
1: {牛奶, 面包, 黄油}
2: {牛奶, 面包}
3: {啤酒, 面包}
相应的FP树将会有如下形态:
root|面包:3|-------------------| |
牛奶:2 啤酒:1| |
黄油:1 (结束)|
(结束)
构建FP树
第一步:扫描数据库并排序
首先,算法会扫描整个事务数据库以找出每个项的出现次数,并根据频率对它们进行排序。
例如,对于上面的数据集,排序后的项列表是:面包:3, 牛奶:2, 黄油:1, 啤酒:1
第二步:构建树
然后,每一笔事务都按照排序后的项列表添加到FP树中。这个步骤是增量的,意味着如果一个项组合(如{‘牛奶’, ‘面包’})在多个事务中出现,那么在树中相应的路径将只被创建一次,但频率会累加。
例如,第一个和第二个事务都包含{‘牛奶’, ‘面包’},因此FP树中的路径是root -> 面包 -> 牛奶,并且“牛奶”这个节点的频率是2。
挖掘频繁项集
一旦FP树构建完成,下一步是从这个树中挖掘频繁项集。这通常通过递归地遍历FP树来完成,从叶子节点开始,逆向回溯到根节点,同时收集路径上的所有项。
例如,在上面的FP树中,从“黄油”节点开始逆向回溯到根节点,会得到一个频繁项集{‘牛奶’, ‘面包’, ‘黄油’}。
优化:条件FP树
为了进一步提高效率,FP-Growth算法使用了一种称为**条件FP树(Conditional FP-Tree)**的技术。这是基于现有FP树生成的新FP树,但只考虑某一个或几个特定项。
例如,如果我们只关心包含“牛奶”的事务,可以构建一个只包含“牛奶”的条件FP树。这个子树会忽略所有不包含“牛奶”的事务和项,从而减少需要处理的数据量。
通过这种方式,FP-Growth算法不仅大大减少了数据挖掘所需的时间和资源,还在频繁项集挖掘中设置了新的效率标准。
三、优缺点比较
FP-Growth算法在数据挖掘中有着广泛的应用,特别是在频繁项集和关联规则挖掘方面。然而,像所有算法一样,FP-Growth也有其优点和缺点。本节将详细探讨这些方面。
优点
1. 效率
效率 是FP-Growth算法最显著的优点之一。由于其紧凑的数据结构(FP树)和两次数据库扫描,该算法能在较短的时间内找到所有频繁项集。
- 例子: 想象一下,如果你有一个包含上百万条事务的大型数据库,使用Apriori算法可能需要多次扫描整个数据库,耗费大量时间。相对地,FP-Growth算法通常只需要两次扫描,大大提高了效率。
2. 内存利用
内存利用 是通过使用FP树,FP-Growth算法优化了存储需求,因为它压缩了事务数据,仅保存了有效信息。
- 例子: 如果原始数据包括了数百个商品和数万条事务,用传统的方法储存可能会占用大量内存。但是FP-Growth通过构建FP树,能够以更紧凑的形式存储这些信息。
3. 可扩展性
可扩展性 是指算法能有效处理大规模数据集。FP-Growth算法通常可以轻松处理大量的数据。
- 例子: 在数据集规模从1000条事务扩展到10万条事务时,FP-Growth算法的运行时间通常是线性增长的,而不是指数增长。
缺点
1. 初始化成本
初始化成本 主要是构建初始FP树所需的时间和资源,这在某些情况下可能会相对较高。
- 例子: 如果事务数据库中的项非常多且分布不均,构建初始FP树可能会消耗较多时间。
2. 不适用于所有数据类型
不适用于所有数据类型 指的是FP-Growth算法主要针对事务数据,可能不适用于其他类型的数据结构或模式。
- 例子: 在文本挖掘或者网络分析中,数据通常以图或者矩阵的形式出现,FP-Growth在这类场景下可能不是最有效的方法。
3. 参数敏感性
参数敏感性 是指算法性能可能会受到支持度阈值等参数的影响。
- 例子: 如果设置的支持度阈值过低,可能会生成大量不太有用的频繁项集;反之,过高的阈值可能会遗漏重要的模式。
通过理解FP-Growth算法的这些优缺点,我们可以更加明智地决定何时使用这个算法,以及如何优化其参数以获得最佳性能。
四、算法实战
问题描述
问题描述:假设我们有一个购物事务数据库,每一条事务都包含用户购买的商品列表。我们的目标是找到在这些事务中频繁出现的商品组合。
- 输入:一组购物事务。每个事务是一个商品列表。
transactions = [['牛奶', '面包', '黄油'],['牛奶', '面包'],['啤酒', '面包'] ] - 输出:频繁项集和它们的支持度。
[('面包', 3), ('牛奶', 2), ('牛奶', '面包', 2), ('黄油', '牛奶', '面包', 1), ...]
环境准备
首先,确保你已经安装了Python和PyTorch。你也可以使用pip来安装pyfpgrowth库,这是一个用于实现FP-Growth算法的Python库。
pip install pyfpgrowth
Python实现
以下是使用pyfpgrowth库来找出频繁项集的Python代码:
import pyfpgrowth# 输入数据:事务列表
transactions = [['牛奶', '面包', '黄油'],['牛奶', '面包'],['啤酒', '面包']
]# 设置支持度阈值,这里我们使用2作为最小支持度
min_support = 2# 使用pyfpgrowth找出频繁项集和它们的支持度
patterns = pyfpgrowth.find_frequent_patterns(transactions, min_support)# 输出结果
print("频繁项集及其支持度:", patterns)
输出:
频繁项集及其支持度: {('牛奶',): 2, ('牛奶', '面包'): 2, ('面包',): 3}
这个输出告诉我们,'面包’出现了3次,'牛奶’出现了2次,而组合{‘牛奶’, ‘面包’}也出现了2次。
五、总结
在本篇博客中,我们全面地探讨了FP-Growth算法,从其基本原理和数学模型到实际应用和Python代码实现。我们也深入讨论了这一算法的优缺点,以及如何在实际场景中应用它。
-
数据结构的威力:FP-Growth算法所使用的FP树是一种极为高效的数据结构,它不仅降低了算法的内存需求,而且大大提高了执行速度。这体现了合适的数据结构选择对算法性能的重要性。
-
参数优化的重要性:虽然FP-Growth算法相对容易实现和应用,但合适的参数选择(如支持度和置信度阈值)仍然是获取有用结果的关键。这强调了算法应用中的“艺术性”,即理论和实践相结合。
-
算法的局限性:FP-Growth算法虽然在事务数据挖掘方面表现出色,但并不适用于所有类型的数据或问题。因此,在选择算法时,应根据具体应用场景和需求进行全面评估。
-
并行和分布式计算的潜力:虽然本文没有涉及,但值得注意的是,FP-Growth算法有着良好的并行化和分布式计算潜力。这意味着该算法可以很容易地扩展到更大的数据集和更复杂的计算环境。
-
跨领域应用:频繁项集挖掘不仅在市场分析中有应用,还广泛应用于生物信息学、网络安全和社交网络分析等多个领域。因此,掌握FP-Growth算法等数据挖掘技术对于任何希望从大规模数据中提取有价值信息的人来说,都是非常有用的。
通过深入理解和实践FP-Growth算法,我们可以更有效地从大量数据中提取有用的模式和信息,从而在多个领域内做出更加明智和数据驱动的决策。希望本篇博客能够帮助你更全面地理解这一强大的数据挖掘工具,以及如何在实际问题中应用它。
关注TechLead,分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验,同济本复旦硕,复旦机器人智能实验室成员,阿里云认证的资深架构师,项目管理专业人士,上亿营收AI产品研发负责人。
相关文章:

FP-Growth算法全解析:理论基础与实战指导
目录 一、简介什么是频繁项集?什么是关联规则挖掘?FP-Growth算法与传统方法的对比Apriori算法Eclat算法 FP树:心脏部分 二、算法原理FP树的结构构建FP树第一步:扫描数据库并排序第二步:构建树 挖掘频繁项集优化&#x…...

Jmeter 分布式压测,你的系统能否承受高负载?
你可以使用 JMeter 来模拟高并发秒杀场景下的压力测试。这里有一个例子,它模拟了同时有 5000 个用户,循环 10 次的情况。 请求默认配置 token 配置 秒杀接口 结果分析 但是,实际企业中,这种压测方式根本不满足实际需求。下…...

什么是浮动密封?
浮动密封也称为机械面密封或双锥密封,是一种用于各种行业和应用的特殊类型的密封装置。它旨在提供有效的密封和保护,防止污染物的进入以及旋转设备中润滑剂或液体的润滑剂泄漏。 浮动密封件由相同的金属环组成,这些金属环称为密封环…...

浅析前端单元测试
对于前端来说,测试主要是对HTML、CSS、JavaScript进行测试,以确保代码的正常运行。 常见的测试有单元测试、集成测试、端到端(e2e)的测试。 单元测试:对程序中最小可测试单元进行测试。我们可以类比对汽车的测试&…...

线上mysql表字段加不了Fail to get MDL on replica during DDL synchronize,排查记录
某天接近业务高峰期想往表里加字段加不了,报错:Fail to get MDL on replica during DDL synchronize 遂等到业务空闲时操作、还是加不了, 最后怀疑是相关表被锁了,或者有事务一直进行(可能这俩是一个意思)&…...
vue3使用element plus的时候组件显示的是英文
问题截图 这是因为国际化导致的 解决代码 import zhCn from "element-plus/es/locale/lang/zh-cn"; 或者 import zhCn from "element-plus/lib/locale/lang/zh-cn";const localezhCn<el-config-provider :locale"locale"><el-date-pic…...
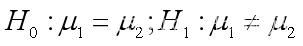
Matlab参数估计与假设检验(举例解释)
参数估计分为点估计和区间估计,在matlab中可以调用namefit()函数来计算参数的极大似然估计值和置信区间。而数据分析中用得最多的是正态分布参数估计。 例1 从某厂生产的滚珠中抽取10个,测得滚珠的直径(单位:mm)为x[…...

qt响应全局热键
QT5 QWidget响应全局热键-百度经验...

android 代码设置静态Ip地址的方法
在Android中,可以使用以下代码示例来设置静态IP地址: import android.content.Context import android.net.ConnectivityManager import android.net.LinkAddress import android.net.Network import android.net.NetworkCapabilities import android.ne…...
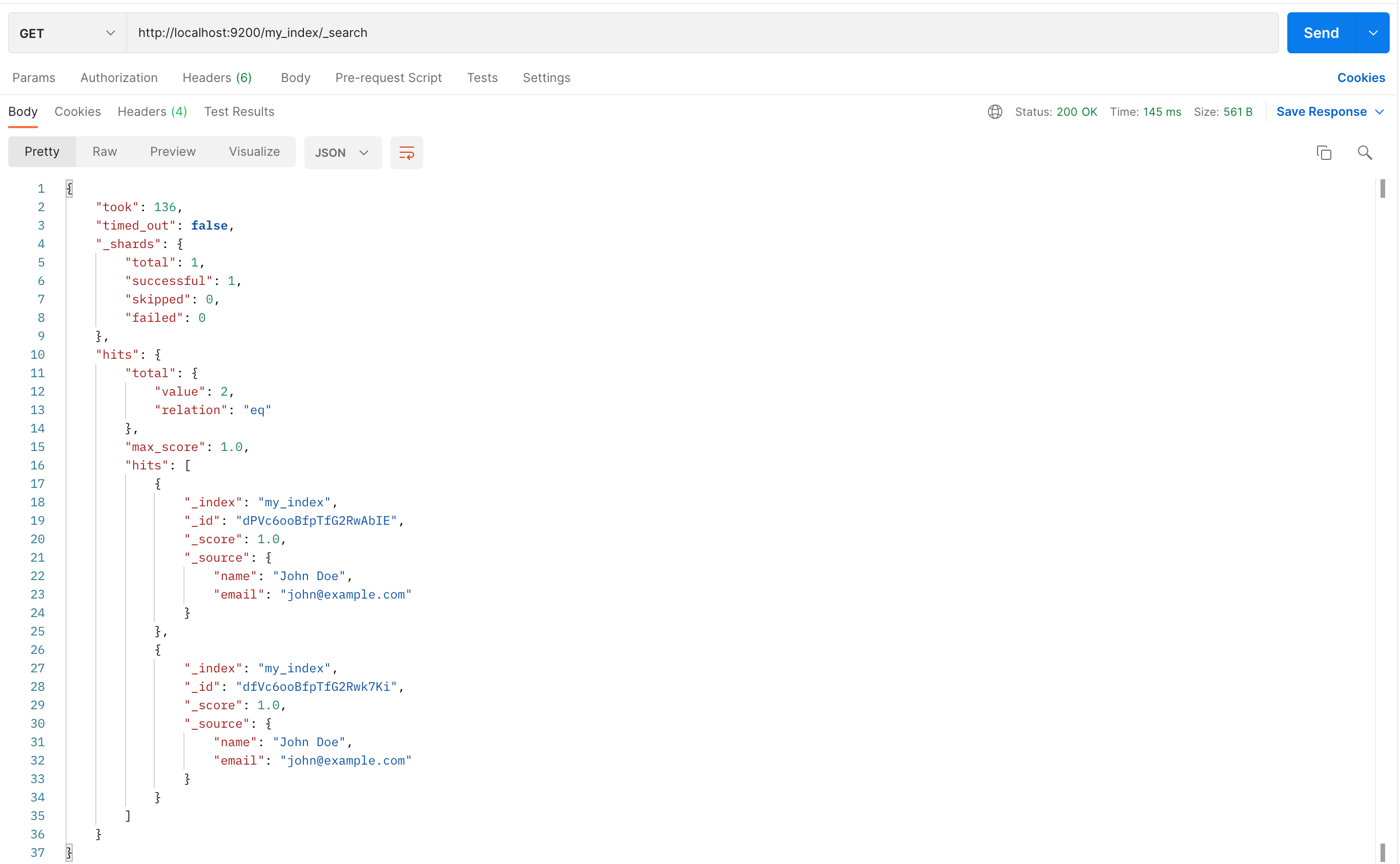
Elasticsearch安装访问
Elasticsearch 是一个开源的、基于 Lucene 的分布式搜索和分析引擎,设计用于云计算环境中,能够实现实时的、可扩展的搜索、分析和探索全文和结构化数据。它具有高度的可扩展性,可以在短时间内搜索和分析大量数据。 Elasticsearch 不仅仅是一个…...
:setState为什么使用异步机制?)
面试题-React(十):setState为什么使用异步机制?
在React中,setState的异步特性和异步渲染机制是开发者们经常讨论的话题。为什么React选择将setState设计为异步操作?异步渲染又是如何实现的?本篇博客将深入探究这些问题,通过代码示例解释为什么异步操作是React的一大亮点。 一、…...
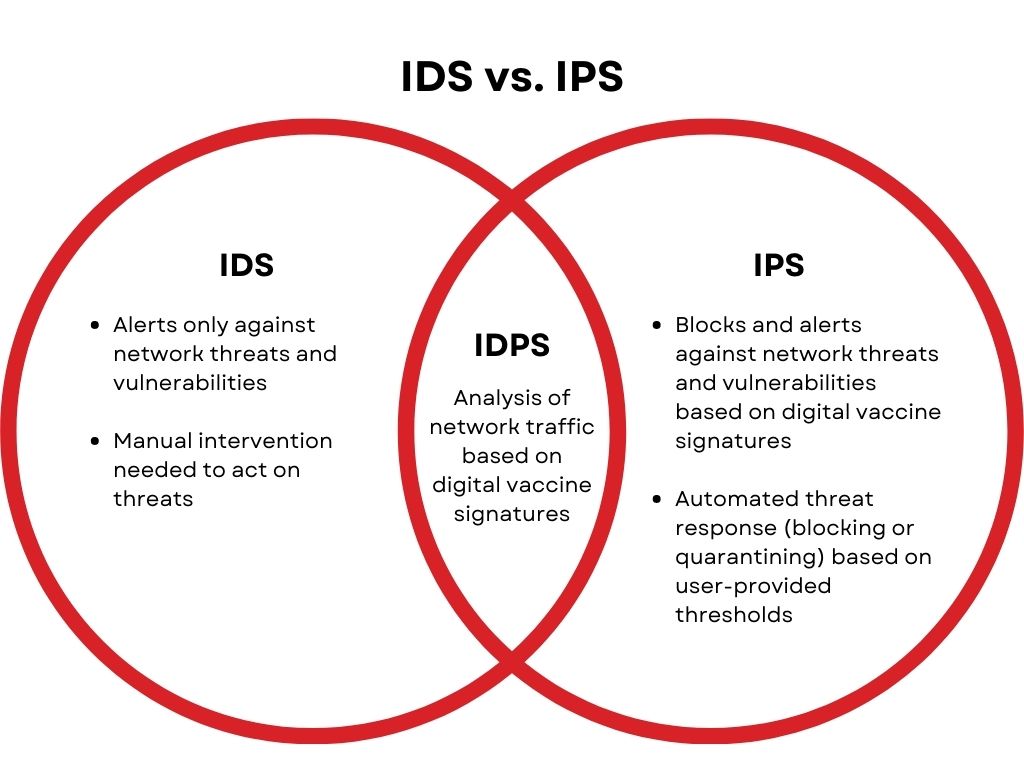
入侵防御系统(IPS)网络安全设备介绍
入侵防御系统(IPS)网络安全设备介绍 1. IPS设备基础 IPS定义 IPS(Intrusion Prevention System)是一种网络安全设备或系统,用于监视、检测和阻止网络上的入侵尝试和恶意活动。它是网络安全架构中的重要组成部分&…...

【Linux基础】Linux的基本指令使用(超详细解析,小白必看系列)
👉系列专栏:【Linux基础】 🙈个人主页:sunnyll 目录 💦 ls 指令 💦 pwd指令 💦cd指令 💦touch指令 💦mkdir指令(重要) 💦rmdir指令…...

【无标题】Test
短视频平台的那些事 前言 过去几年,我一直专注于短视频平台的建设和开发工作。在这个过程中,我发现这个领域有着非常多的挑战和机遇,也涌现出了许多新的技术和创新。今天大家分享我个人的一些经验,希望能够为大家带来一些启发和帮…...

1576. 替换所有的问号
1576. 替换所有的问号 C代码:自己写的 char * modifyString(char * s){int n strlen(s);for (int i 0; i < n; i){if (s[i] ?) {if (i ! 0 && i ! n-1) {for (int j 0; j < 26; j) {if (a j ! s[i-1] && a j ! s[i1]) {s[i] a j;br…...
MySQL学习笔记(快速入门)
Mysql快速入门 一、数据库相关概念1.启动数据库2. 客户端连接3. 数据模型4.关系型数据库RDBMS 二、SQL语言1. 通用语法2. SQL分类 三、DDL数据定义语言1. 数据库操作2. 表操作(1) 查询当前数据库所有表show tables;(2) 查询表的结…...

使用DNS查询Web服务器IP地址
浏览器并不具备访问网络的功能,其最终是通过操作系统实现的,委托操作系统访问服务器时提供的并不是浏览器里面输入的域名而是ip地址,因此第一步需要将域名转换为对应的ip地址 域名:www.baidu.com ip地址是一串数字 tcp/ip的网络结…...
docker虚拟网桥和业务网段冲突处理
ifconfig查看docker虚拟网桥ip地址 docker inspect --format{{.Name}} - {{range .NetworkSettings.Networks}}{{.IPAddress}}{{end}} $(docker ps -aq)查询所有容器的ip 修改docker-compose networks networks xxx-network: driver: bridge ipam: c…...

axios登录,登出接口的简单封装步骤详解!
目录 总结一、步骤1.安装Axios:2.axios对象封装3.请求api封装4.使用pinia临时库保存响应信息(按需求用)5.最后,在组件中使用! 总结 封装axios对象,编写公共请求代码、添加拦截逻辑、然后分层实现axios请求…...

九大装修收纳空间的设计,收藏备用!福州中宅装饰,福州装修
如果房子面积不大,收纳设计就显得非常重要。其实装修房子中很多地方都可以做收纳,九大空间每一处都可以放下你的东西,让你摆脱收纳烦恼。 收纳空间少的话,装修完后住久了怕会乱成一窝,因此装修的时候,收纳…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
持续交付的进化:从DevOps到AI驱动的IT新动能
文章目录 一、持续交付的本质:从手动到自动的交付飞跃关键特性案例:电商平台的高效部署 二、持续交付的演进:从CI到AI驱动的未来发展历程 中国…...
