linux如何删除最近操作的日志
Linux系统下,不同的应用程序可能会生成不同的日志文件。如果你想要删除最近一段时间内的操作日志,可以使用一些命令来完成。
以下是一些常见的命令:
-
dmesg:该命令用于显示内核环境下的运行信息和警告信息。如果你需要清空dmesg缓冲区,可以使用以下命令:
sudo dmesg -c -
history:该命令用于显示用户在终端中执行的命令历史记录。如果你想要清空操作历史记录,可以使用以下命令:
history -c注意,这将仅删除.bash_history文件中的命令历史记录,而不是其他日志文件。
-
syslog:该命令用于显示系统日志。如果你想要删除最近一段时间内的syslog记录,可以使用以下命令:
sudo truncate -s 0 /var/log/syslog该命令将清空/var/log/syslog文件中的内容。
-
auth.log:该命令用于显示系统认证记录。如果你想要删除最近一段时间内的auth.log记录,可以使用以下命令:
sudo truncate -s 0 /var/log/auth.log该命令将清空/var/log/auth.log文件中的内容。
需要注意的是,删除日志文件可能导致无法查找之前的操作记录和故障排查。请谨慎使用该命令来删除日志文件。如果希望管理日志文件的空间,可以考虑使用日志轮替工具(如logrotate)来管理日志文件的大小,并确保及时备份重要日志。
相关文章:

linux如何删除最近操作的日志
Linux系统下,不同的应用程序可能会生成不同的日志文件。如果你想要删除最近一段时间内的操作日志,可以使用一些命令来完成。 以下是一些常见的命令: dmesg:该命令用于显示内核环境下的运行信息和警告信息。如果你需要清空dmesg缓…...

android端MifareClassicTool
github地址 GitHub - ikarus23/MifareClassicTool: An Android NFC app for reading, writing, analyzing, etc. MIFARE Classic RFID tags. 开源项目 下载: https://www.icaria.de/mct/releases/ 功能 1、读取Mifare Classic卡片 2、编辑并保存卡片的数据 3、写入Mifare C…...
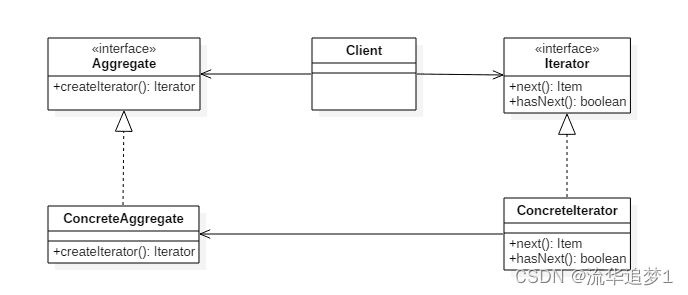
设计模式 - 迭代器模式
目录 一. 前言 二. 实现 三. 优缺点 一. 前言 迭代器模式是一种行为型设计模式,它提供了一种统一的方式来访问集合对象中的元素,而不暴露集合内部的表示方式。简单地说,就是将遍历集合的责任封装到一个单独的对象中,我们可以按…...
Docker之Dockerfile搭建lnmp
目录 一、搭建nginx 编辑 二、搭建Mysql(简略版) 三、搭建PHP 五、补充 主机名ip地址主要软件mysql2192.168.11.22Docker 代码示例 systemctl stop firewalld systemctl disable firewalld setenforce 0docker network create --subnet172.18.…...
排序算法——选择排序
一、介绍: 选择排序就是按照一定的顺序从选取第一个元素索引开始,将其储存在一个变量值中,根据排序规则比较后边每一个元素与这个元素的大小,根据排序规则需要,变量值的索引值进行替换,一轮遍历之后&#x…...

【数据结构C/C++】双向链表的增删改查
文章目录 CC408考研各数据结构C/C代码(Continually updating) 对我个人而言,在开发过程中使用的比较多的就是双向链表了。 很多重要的代码优化都会使用到基于双向链表实现的数据机构。 比如我们常用的HashMap,我们知道Key其实是无…...
Godot 添加Nuget 引用
前言 我的Godot 专栏 我在之前的文章中,解决了Visual Studio 如何去调试正在运行的Godot 程序。Godot 对于C# 的支持只剩下一个,那就是Nuget 添加。 Godot VisualStudio外部编辑器设置 添加Nuget Nuget 添加还是非常的容易的。我们直接添加一个最常用的…...

IC工程师职场必备《经典Verilog100多个代码案例》(附下载)
对于IC行业的人员而言,Verilog是最基础的入门,用于数字电路的系统设计,很多的岗位都会用到,可对算法级、门级、开关级等多种抽象设计层次进行建模。 Verilog由于其简单的语法,和C语言的相似性,目前被各大公…...
springboot项目做成公共项目
一:引言 最近碰到个需求,就是把我项目做成一个公共的提供jar包给别人使用,我也是捣鼓了一段时间去研究这个问题,这个东西其实就是A 项目提供jar包给B项目,B项目只要引入A项目的jar包就可以使用A项目的功能。 问题一&…...
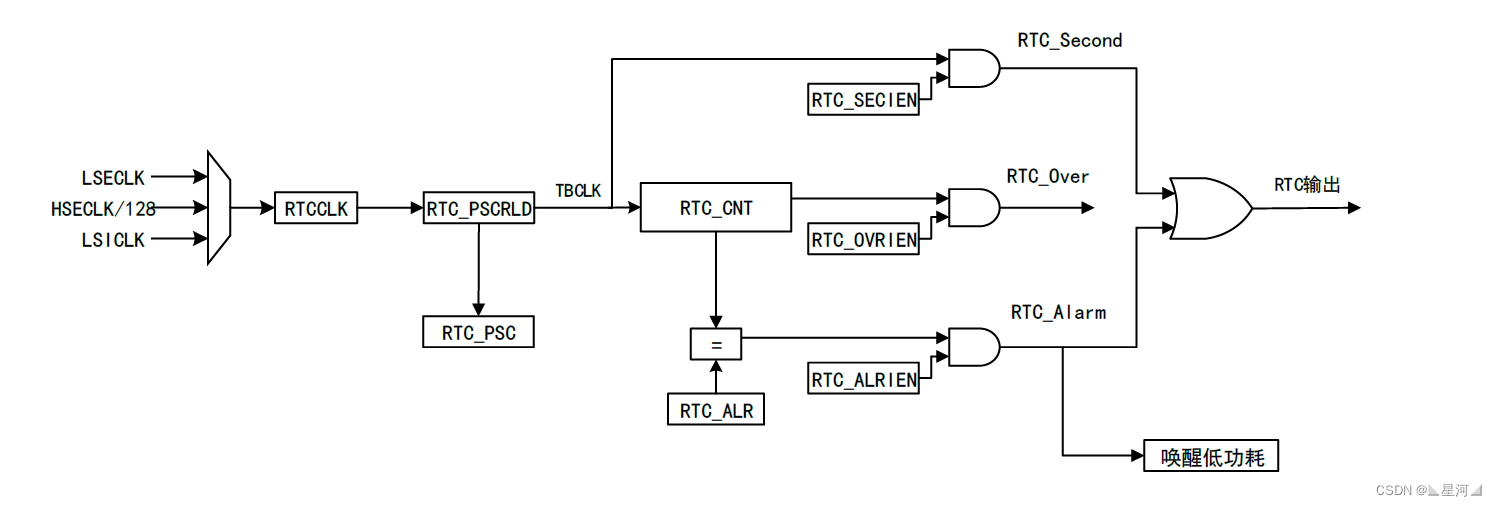
RTC 时间、闹钟
实时时钟RTC是一个独立的定时器。RTC模块拥有一个连续计数的计数器,在软件配置下,可以提供时钟日历的功能。修改计数器的值可以重新设置当前时间和日期 RTC还包含用于管理低功耗模式的自动唤醒单元。 在掉电情况下 RTC仍可以独立运行 只要芯片的备用电源…...
【yolo系列:yolov7训练添加spd-conv】
系列文章目录 yolov7训练添加spd-conv 文章目录 系列文章目录一、spd-conv是什么?二、使用步骤1.第一步:先在models/common.py加上2.第二步:models/yolo.py加上2.第三步:修改yolov7的yaml文件 总结 提示:以下是本篇文…...
面向对象设计-UML六种箭头含义
目录 UML概述UML语义UML表示法 六种常用关系标识方法泛化实现依赖关联聚合组合 本文参考文章 https://blog.csdn.net/qq_25091281/article/details/123801862 UML概述 UML (Unified Modeling Language)为面向对象软件设计提供统一的、标准的、可视化的建模语言。适用于描述以…...

一本没有任何数学公式的自然语言处理入门书
ChatGPT 时代来了,AI 从旧时王谢堂前燕,飞入寻常百姓家。越来越多非 AI 领域 的软件开发者涌进 NLP(自然语言处理)领域。在这个快速发展的时代,如果这些软件开发 者要像读书那样先读 4 年本科、2 年硕士、3 年博士才能搞 AI,风口早…...

【数据结构C/C++】多维数组的原理、访问方式以及作用
文章目录 什么是多维数组?代码讲解使用方式为什么指针遍历的方式是这样子的?(助你理解指针的含义)使用场景408考研各数据结构C/C代码(Continually updating) 什么是多维数组? 在C语言中&#x…...
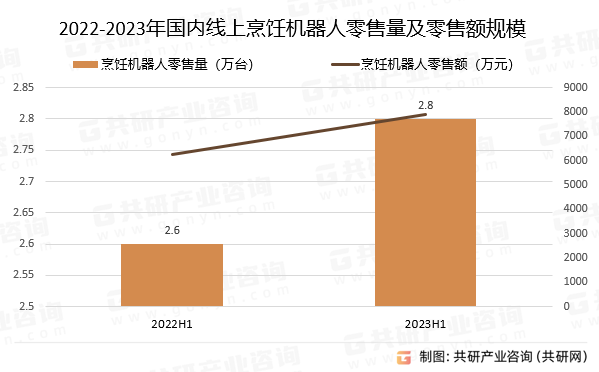
2023年中国烹饪机器人市场发展概况分析:整体规模较小,市场仍处于培育期[图]
烹饪机器人仍属于家用电器范畴,是烹饪小家电的进一步细分,它是烹饪小家电、人工智能和服务机器在厨房领域的融合。烹饪机器人是一种智能化厨房设备,可以根据预设的程序实现自动翻炒和烹饪,是多功能料理机和炒菜机结合的产物。 烹…...

Android原生实现控件选择背景变色方案(API28及以上)
Android控件点击/选择后控件背景变色的实现方式有很多种,例如使用selector的xml文件实现。这里介绍一下另一种Android原生的点击/选择实现方案(API28及以上),也就是ColorStateListDrawable。 ColorStateListDrawable是一个可根据不…...
为什么要学C语言及C语言存在的意义
为什么要学C语言及C语言存在的意义 汇编生C,C生万物。linus说自己最喜欢的语言就是C语言,因为看到写出的代码就能想到对应的汇编码。一方面说明C语言足够简洁,没有像C中一样的复杂概念封装,另一方面也说明C语言足够的底层…...

数据结构——空间复杂度
空间复杂度,与算法运行时所需的内存空间有关。 默认问题规模为n。 举例案例,具体分析。 1.全是普通变量 2.一维数组 3.二维数组 4.递归--变量 不递归的时候空间复杂度是O(1),递归的话递归n次,乘以n,所以空间复杂度…...

uniapp:swiper-demo效果
单元格轮播 <swiper class"swiper1" :circular"true" :autoplay"true" interval"3000" previous-margin"195rpx" next-margin"195rpx"><swiper-item v-for"(item,index) in 5" :key"inde…...
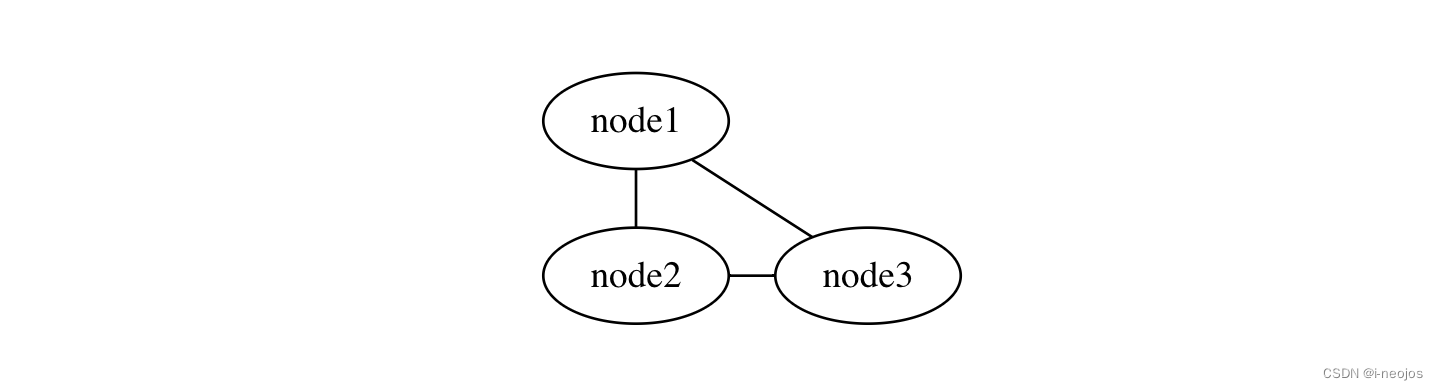
Graphviz 作图工具
选择 Graphviz 作为作图工具,主要是想通过代码创建图标,按照 Graphviz 的代码规范就可以生成 svg 的图片。当然,这样的工具也有很多,有些 markdown 编辑器也做了集成,比如: flowchart.jsMermaid 了解 Gra…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...
