算法设计与分析期末考试复习(二)
分治法
将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。最好使子问题的规模大致相同。
- 分解(Divide):将一个难以直接解决的大问题,分割成一些规模较小的子问题,这些子问题互相独立,且与原问题相同。
- 递归求解子问题,若问题足够小则直接求解。
- 将各个子问题的解合并得到原问题的解。
求二叉树深度
int get_depth(BTPtr pbt){int dL,dR=0;if(pbt == NULL){return 0;}if((!ptb->lchild) && (!ptb->rchild)){return 1;}dL = get_depth(pbt->lchild);dR = get_depth(pbt->rchild);return 1 + ((dL>dR)?dL:dR);
}
分治法所能解决的问题一般具有四个特征:
- 该问题的规模缩小到一定的程序就可以容易地解决。
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
- 利用子问题的解可以合并得到原始问题的解。
- 各个子问题是相互独立的。
二分搜索技术,每执行一次算法while循环,待搜索数组的大小减少一半,因此最坏时间复杂度O(log n)
int BinarySearch(int a[],int x,int left,int right){while(left <= right){int mid = (left + right)/2;if(a[mid] == x){return mid;}else if(a[mid] < x){left = mid + 1;}else{right = mid - 1;}}return -1;
}
Master定理(递归复杂度判定定理)

大整数的乘法:将两个n位大整数相乘
传统逐位相乘、错位相加的传统方法:O(n2),效率太低。
分治法:将该问题分解为若干个规模较小的相同问题。

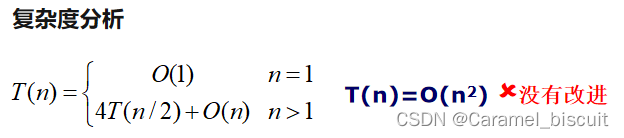
为了降低时间复杂度,必须减少乘法的次数。
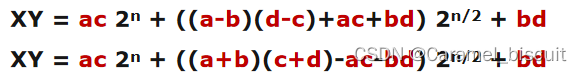
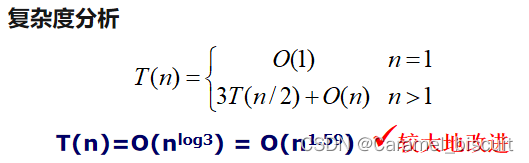
两个XY复杂度都相同,但(a+b),(c+d)可能得到(n/2)+1位的结果,使问题的规模变大,故不选择第2种方案。
矩阵乘积的传统算法,时间复杂度O(n3)
void multi(int A[],int B[],int C[]){for(int i=1; i<=n ;i++){for(int j=1;j<=n;j++){C[i][j] = 0;for(int k=1 ;k<=n; k++){C[i][j] += A[i][k]*B[k][j];}}}
}
分治法:矩阵乘法

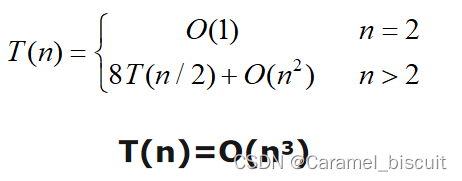
为了降低时间复杂度,必须减少乘法的次数。

棋盘覆盖问题:在一个2kx2k个方格组成的棋盘中,要求用图(b)所示的4种L形态骨牌覆盖给定的特殊棋盘,覆盖给定特殊棋盘上除特殊方格以外的所有方格,任何2个L型骨牌不得重叠覆盖。
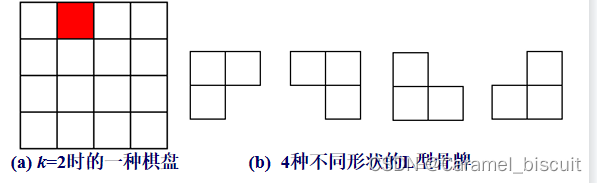
分治策略技巧:使每个子棋盘均包含一个特殊的方格,从而将原问题分解为规模较小的棋盘覆盖问题。
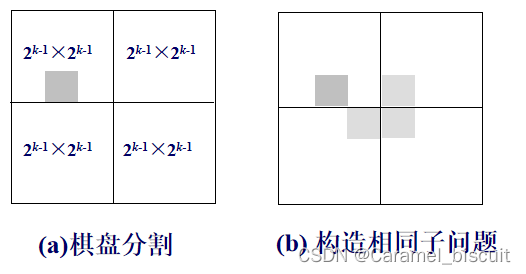
棋盘覆盖问题中数据结构的设计:
- 棋盘:用二维数组board[size][size]表示一个棋盘,其中size=2k。为了在递归处理的过程中使用同一个棋盘,将数组board设为全局变量。
- 子棋盘:在棋盘数组board[size][size]中,用子棋盘左上角的tr、tc和棋盘边长s表示。
- 特殊方格:用board[dr][dc]表示,dr和dc是该特殊方格在棋盘数组board中的下标。
- L型骨牌:一个2k×2k的棋盘中有一个特殊方格,所以,用到L型骨牌的个数为(4k-1)/3,将所有L型骨牌从1开始连续编号,用一个全局变量t表示。
void ChessBoard(int tr,int tc,int dr,int dc,int size){if(size == 1) return; //棋盘只有一个方格,且是特殊方格。t++;//L型骨牌号,已经初始化为0。s = size/2;//划分棋盘if(dr<tr+s && dc<tc+s){ //特殊方格在棋盘左上角ChessBoard(tr,tc,dr,dc,s);}else{ //用t号L型骨牌覆盖右下角,再递归处理子棋盘board[tr+s-1][tc+s-1] = t;ChessBoard(tr,tc,tr+s-1,tc+s-1,s);}if(dr<tr+s && dc >= tc+s){ChessBoard(tr,tc+s,dr,dc,s);}else{board[tr+s-1][tc+s] = t;ChessBoard(tr,tc+s,tr+s-1,tc+s,s);}if(dr>=tr+s && dc<tc+s){ChessBoard(tr+s,tc,dr,dc,s);}else{board[tr+s][tc+s-1] = t;ChessBoard(tr+s,tc,tr+s,tc+s-1,s);}if(dr >= tr+s && dc >= tc+s){ChessBoard(tr+s,tc+s,dr,dc,s);}else{board[tr+s][tc+s] = t;ChessBoard(tr+s,tc+s,tr+s,tc+s,s);}
}
- 当k>0时,将2的k次幂乘以2的k次幂分隔成为4个2的k-1次幂乘以2的k-1次幂子棋盘。
- 特殊方格必位于4个较小棋盘之一中,其余3个子棋盘中午特殊方格。
- 为了将这3个特殊方格的子棋盘转化为特殊棋盘,可以用一个L型骨牌将这3个较小棋盘的汇合处覆盖,这3个子棋盘上被L型骨牌覆盖的方格就成为该棋盘上的特殊方格,从而将原问题转换成4个较小规模的棋盘覆盖问题。递归地使用这种分割,直至棋盘简化为1*1棋盘。

快速排序:在数组中确定一个记录作为划分元,将数组中关键字小于划分元的记录移动到划分元之前,将数组中大于划分元的记录移动到划分元之后。
int Partition(int *arr,int L,int R){int left = L;int right = R;int pivot = arr[left];while(left < right){while(left<right && arr[right]>=pivot)right--;if(left < right){arr[left] = arr[right];}while(left<right && arr[left]<=pivot)left;if(left<right){arr[right] = arr[left];}if(left == right){arr[left] = pivot;return left;}}
}void QuickSort(int *arr,int L,int R){if(L < R){int position = Partition(arr,L,R);quickSort(arr,L,position-1);quickSort(arr,position+1,R)}
}
最好情况:T(n)=O(nlogn)(每次总是选到中间值作为划分元)
最坏情况:T(n)=O(n2)(每次总是选到最小或最大元素作为划分元)
算法性能与系列中关键字的排列顺序和划分元的选取有关
- 当初始序列按关键字有序(正序或逆序)时,快速排序蜕化为冒泡排序,此时算法性能最差,时间复杂度为O(n2)。
- 可以用“三者取中”法来选取划分元,设:数组首记录为r[s]、尾记录为r[t],取:r[s]、r[t]和r[(s+t)/2]三者的中间值为划分元。
- 也可采用随机选取划分元的方式
快速排序算法的性能取决于划分的对称性。通过修改算法partition,可以设计出采用随机选择策略的快速排序算法。在a[p:r]中随机选出一个元素作为划分基准,这样可以使划分基准的选择是随机的,从而可以期望划分是比较对称的。
int RandomizedPartition(int a[],int p,int r){int i = random(p,r);swap(a[i],a[p]);Partition(a,p,r)
}
线性时间选择:给定线性序集中n个元素和一个整数k,要求找出这n个元素中第k小的元素,问是否可以在O(n)时间内得到解决,可以采用分治法,模仿快排对输入数组进行递归划分,只对划分出的子数组之一进行递归处理,子数组的选择与划分元和k相关。
int RandSelect(int A[],int start,int end,int k){if(start == end){return A[start];}int i = RandomizedPartition(A,start,end);int n = i-start+1;//左子数组的个数if(k <= n){RandSelect(A,start,n,k);}else{RandSelect(A,i+1,end,k-n;)}
}
线性时间内找到合理划分基准的步骤(select函数)
- 将n个元素划分成n/5个组,每组5个元素,只有可能一个组不是5个元素。
- 用任意一种排序算法对每组中的元素排序。
- 取出每组中的中位数,共n/5个元素。
- 递归调用select函数,找出这n/5元素中的中位数。
- 如果n/5为偶数,就选择2个中位数中较大的一个,以这个选出的元素作为划分基准。
按递增序列,找出下面29个元素的第18个元素:
8,31,60,33,17,4,51,57,49,35,11,43,37,3,13,52,6,19,25,32,54,16,5,41,7,23,22,46,29.
- 把前面29个元素分为6组(ceil(29/5));(8,31,60,33,17),(4,51,57,49,35),(11,43,37,3,13),(52,6,19,25,32),(54,16,5,41,7),(23,22,46,29).
- 提取每一组中的中值元素,构成集合{33,49,13,25,16,29}
- 递归地使用该算法求得集合中的中值,得到m=29.
- 根据m=29,把29个元素划分为3个子数组P={8,17,4,11, 3,13,6,19, 25,16,5,7,23,22},Q={29},R={31,60,33,51,57,49,35,43,37,52,32,54,41,46}
- P中有14个元素,Q中有1个元素,所以18-15=3,对R递归地执行本算法。
- 将R划分成3组(ceil(14/5)):{31,60,33,51,57},{49,35,43,37,52},{32,54,41,46}
- 求取这3组元素的中值元素分别为{51,43,46},这个集合的中值是43.
- 根据43将R划分成3组{31, 33, 35,37,32, 41},{43},{60, 51,57, 49, 52,54, 46}
- 因为k=3,第一个子数组的元素个数大于k,所以放弃后面两个子数组,以k=3对第一个子数组递归调用本算法;
- 将这个子数组分为5个元素为一组: {31,33,35,37,32}、{41},取中值为33。
- 根据33,把第一个子数组划分成{31,32},{33},{35,37};
- 因为k=3,而第一、第二个子数组的元素个数为3,所以33即为所求取的第18个小元素。
int Select(int a[],int start,int end,int k){if(end-start<75){//用某个简单的算法对数组a[start:end]排序return a[start+k-1];}for(int i=0; i<=(end-start-4)/5; i++){//将a[start+5*i]与a[start+4+5*i]的第3小元素与a[start+i]交换位置}//找出中位数中的中位数int x = Select(a,start,start+(end-start-4)/5,(end-start-4)/10);int i = Partition(a,start,end,x); //划分元位置int n = i-start+1; //左数组长度if(k <= n) return Select(a,start,i,k);else{return Select(a,i+1,end,k-n);}
}
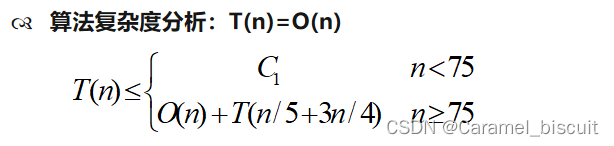
最接近点对:给定平面上的n个点,找出其中的一对点,使得在n个点组成的所有点对中,该点对的距离最小。
直观解法:将每一个点与其他n-1个点的距离算出,找出最小距离,时间复杂度:T(n)=n(n-1)=O(n2)
分治法
- 分解:将n个点的集合分成大小近似相等的两个子集。
- 求解:递归求解两个子集内部的最接近点对。
- 合并:从子空间内部最接近点对,和两个子空间之间的最接近点对中,选择最接近点对。
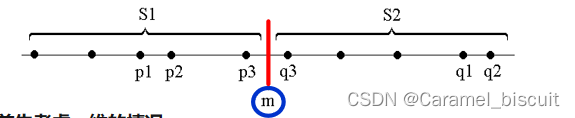
分治法
- 假设我们用x轴上某个点m将S划分为2个子集S1和S2,基于平衡子问题的思想,用S中各点坐标的中位数来作分割点。
- 递归地在S1和S2找出其最接近点对{p1,p2}和{q1,q2}。
- 设d=min{|p1-p2|,|q1-q2|},则S中的最接近点对可能是{p1,p2},或者是{q1,q2},或者是某个{p3,q3},其中p3∈S1且q3∈S2。
- 如果最接近点对是{p3,q3},即|p3-q3|<d:即p3和q3两者之间的基于不超过d,p3∈(m-d, m],q3∈(m, m+d]。
bool Cpair1(S,d){n = |S|;if(n < 2){d = ∞;return false; }m = S中各点坐标的中位数。构造S1和S2 //构造S1={x S|x<=m}, S2={x S|x>m}Cpair(S1,d1);Cpair1(S2,d2);p = max(S1);q = min(S2);d = min(d1,d2,q-p);return true;
}
考虑二维的情况
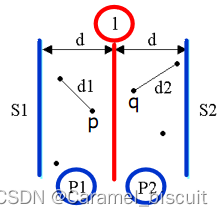
- 选取二维平面的一条垂直线L:x=m作为分割线,其中m为S中各点x坐标的中位数,由此将S分割成S1和S2。
- 递归地在S1和S2上找出其中最小距离d1,d2。
- 设d=min{d1,d2},S中的最接近点对间的距离或者是d,或者是某个点对{p,q}之间的距离,其中p∈S1且q∈S2。如果用符号P1和P2分别表示直线 L 的左右两边宽为d的区域,则必有p∈P1且q∈P2
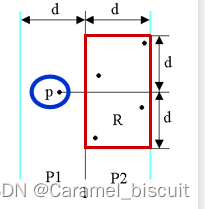
考虑P1中任意一点p,它若与P2中的点q构成最接近点对的候选者,则必由distance(p,q)<d,P2中满足条件的点一定落在矩形R中,矩阵R的大小为dx2d。
由d的定义可知:P2中任何2个点(qi∈S)的距离都不小于d,由此可以推出矩形R中最多只有6个S中的点。
在分治法的合并步骤中最多只需要检查6×n/2=3n个候选者
相关文章:

算法设计与分析期末考试复习(二)
分治法 将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。最好使子问题的规模大致相同。 分解(Divide):将一个难以直接解决的大问题,分割成一些规模较小的子…...
九龙证券|4D毫米波雷达成市场新宠,相关概念股大涨,会贡献多少业绩?
近日,4D毫米波雷达成为A股新宠,相关概念股如经纬恒润(688326.SH)一周内涨幅接近20%,威孚高科(000581.SZ)5个买卖日内涨幅超越25%。 有音讯称特斯拉将在3月1日投资者活动日会宣告新款Model 3的全…...
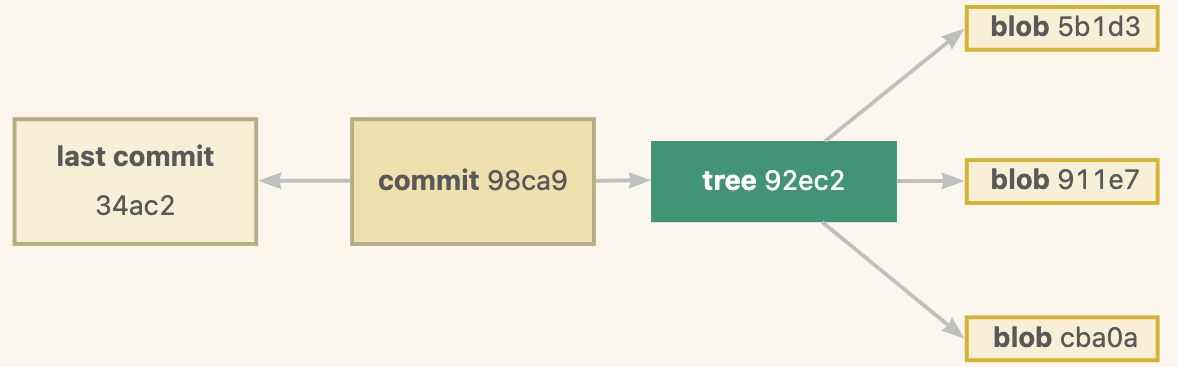
Git天天用,不得不看的那些事
作为一个工作两年的开发同学,git是每天都要接触的工具。但IDEA对git的封装已经满足了日常的代码提交需求,所以一直是以点点点的形式进行代码提交与更新,几乎没用命令行提交过(现在想来也是有些惭愧),对于gi…...
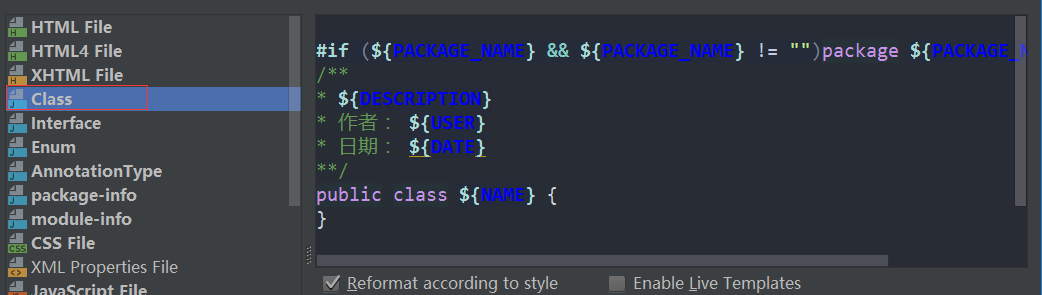
IDE 文档注释使用,模板注释,ide配置templates
文档注释基于javadoc模板 类注释 /*** 暂无介绍** author admin* version 1.0.0* <dt><span class"simpleTagLabel">时间:</span></dt>* <dd>2023/2/24</dd>*/方法注释 /*** 暂无描述** author admin* param args */javadoc相…...

力扣-查询近30天活跃用户数
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:1141. 查询近30天活跃用户数二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.其他总结前言 一、题目&…...

企企通聚源池| 聚合海量资源全网寻源,赋能供采双方撮合交易
目前,我们正处于一个飞速发展的信息时代,随着大数据时代的来临,在企业的日常经营中,数据无处不在,各类数据的采集、整合、分析对企业的发展、决策有着十分重要的作用。数据管理作为企业一项重要的建设工作,…...

【算法数据结构体系篇class09】:链表问题:快慢指针、回文结构、复制、中点,分区、相交
一、链表解题的方法论 1)对于笔试,不用太在乎空间复杂度,一切为了时间复杂度2)对于面试,时间复杂度依然放在第一位,但是一定要找到空间最省的方法二、链表常用数据结构和技巧1)使用容器(哈希表、数组等)2)快…...

实验室信息化管理行业方案
为适应新时代下的管理机制与应用场景,越来越多的检测实验室需对研发部门和实验部门进行全面的、现代化的、电子化的综合管理,帮助检测机构对实验室的规划与计划、项目立项与管理、项目成果、合同,以及基建等工作进行统一的管理,而…...
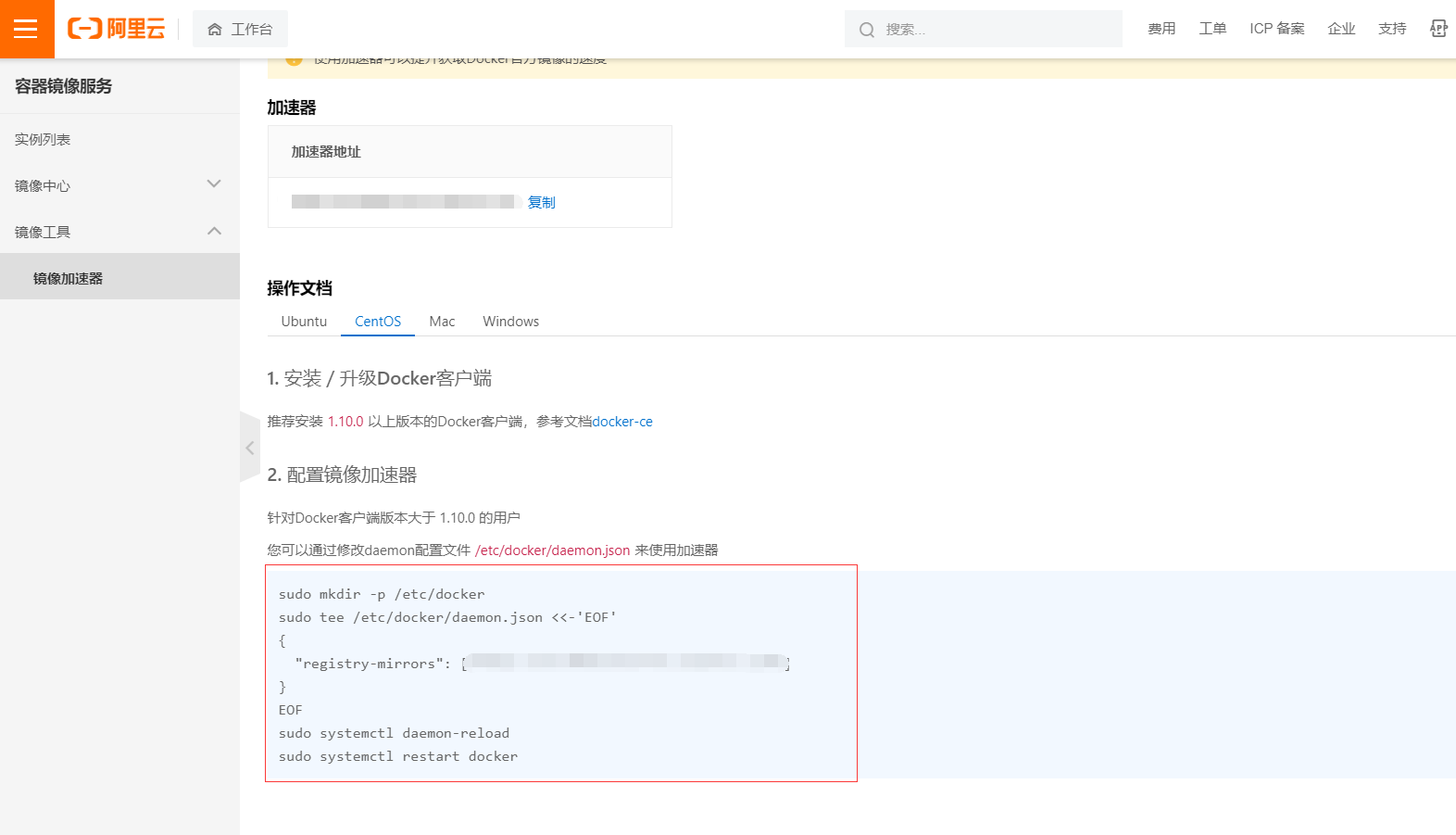
docker学习
docker 环境搭建 MySql # mysql5.7 docker run --name mysql10 -p 3306:3306 -v D:\MySql\conf:/etc/mysql/conf.d -v D:\MySql\data:/var/lib/mysql -e MYSQL_ROOT_PASSWORD123456 -d mysql:5.7docker run --name mysql10 -p 3306:3306 -v /etc/mysql/conf.d:/etc/mysql/co…...

Linux 常用命令
重启 # 重启(root 用户操作) reboot# 强制重启 reboot -f关机 # 关机 # shutdown [OPTION] [TIME] [MESSAGE] shutdown-h 关机 -r 重启-c 取消上一个命令 第二个参数指的是多少分钟后执行操作,以分钟为单位,如果不加时间&am…...
)
数据结构-顺序表(2)
目录 1. 线性表 2. 顺序表 2.1 动态顺序表 3. 接口实现 前期工作 3.1 初始化、销毁与检查容量 3.1.1 初始化 3.1.2 销毁 3.1.3 检查容量 3.2 尾插 3.3 尾删 3.4 头插 3.5 头删 3.6 插入 3.7 删除 顺序表源码 SeqList.h SeqList.c test.c 写在最后ÿ…...
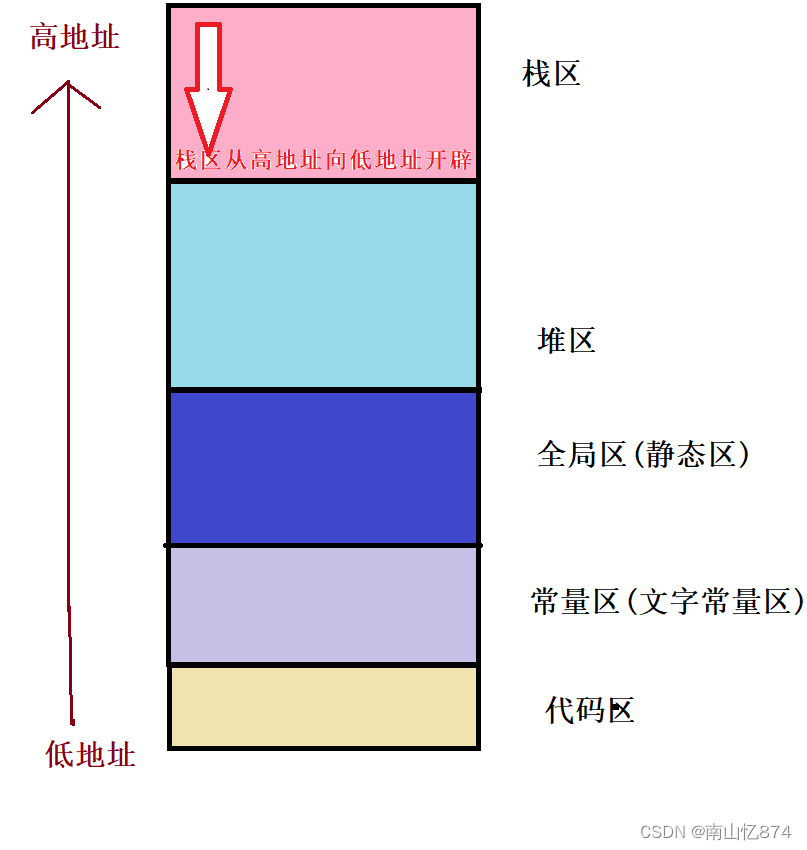
初学C/C++内存管理--new和delete的使用
一,内存分布 栈区: 一般的局部变量和函数的返回数据以及返回地址,函数的参数都在战栈区上开辟空间。栈区开空间一般由编译器自动管理,出了生命周期自动释放。也可以通过一些方式自己手动开辟栈区空间,不过一般用不到…...

【Java】volatile
一、volatile volatile是Java虚拟机提供的轻量级的同步机制,它有3个特性: 1)保证可见性 2)不保证原子性 3)禁止指令重排 当写一个volatile变量时,JMM会把该…...
)
混沌工程 Chaos Mesh 实践经验(持续更新)
使用 k8s JVM故障 Linux内核版本 Linux 系统内核必须为 4.1 及以上版本。 不然会一直失败,可以从Chaos Mesh dashboard前端看到。 对native方法注入故障无效 实测对Thread.sleep(Long) 注入故障无效,猜测是因为对native方法无效,大概因为…...
追梦之旅【数据结构篇】——详解C语言实现链栈
详解C语言实现链栈~😎前言🙌整体实现内容分析💞1.头文件编码实现🙌2.功能文件编码实现🙌3.测试函数功能代码🙌总结撒花💞😎博客昵称:博客小梦 😊最喜欢的座右…...
oracle数据库常用操作
1.连接登录切换用户su - oracle以管理员模式登录到sqlplus:sqlplus / as sysdba oracle登录身份有三种:1.1Normal 普通身份;1.2.sysdba 系统管理员身份;若以 ‘sysdba’ 方式认证,登录用户为 ‘SYS’,为 Or…...
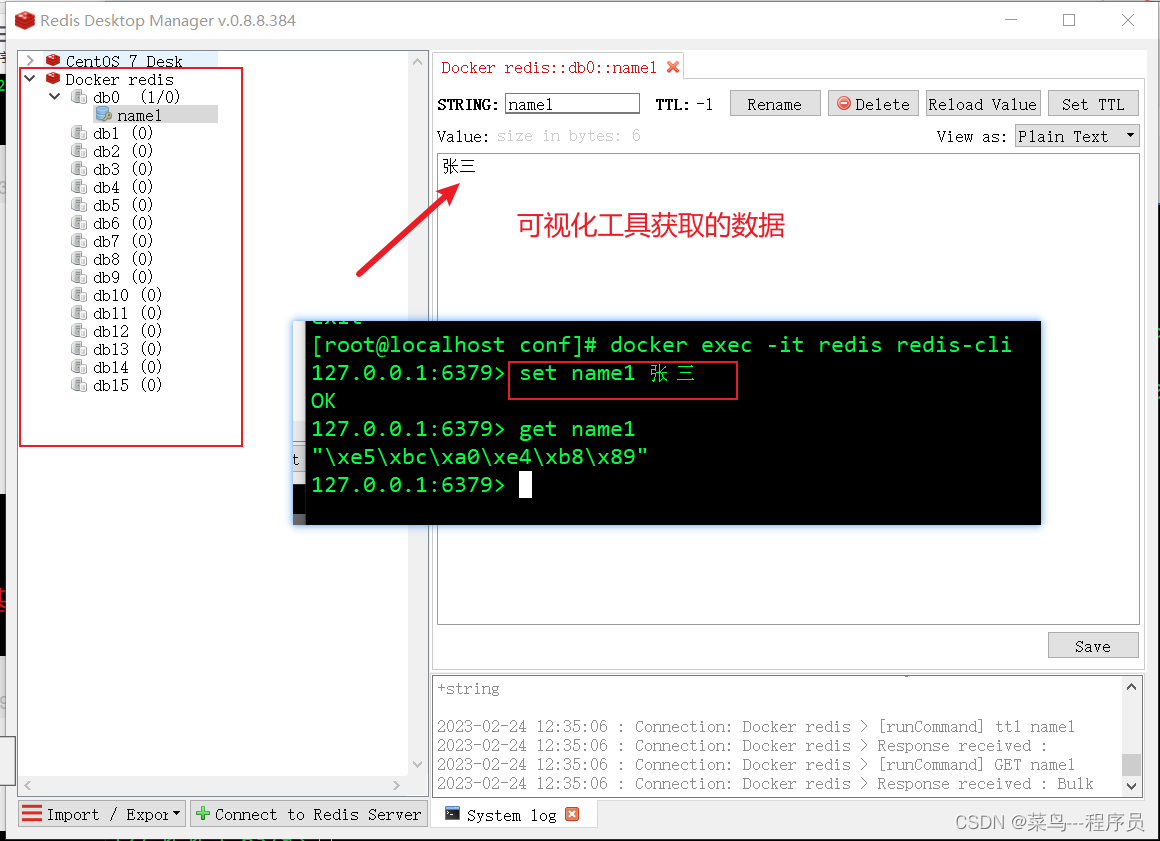
一文教会你如何在Linux系统中使用Docker安装Redis 、以及如何使用可视化工具连接【详细过程+图解】
文章目录1、安装redis2、在外部创建配置文件3、创建redis4、启动测试redis5、数据持久化存储6、使用可视化工具连接redis前言在windows上安装过reids、在linux上也安装过redis,但是都没有docker上安装redis方便。这里给出docer安装redis的相关教程1、安装redis 默认…...
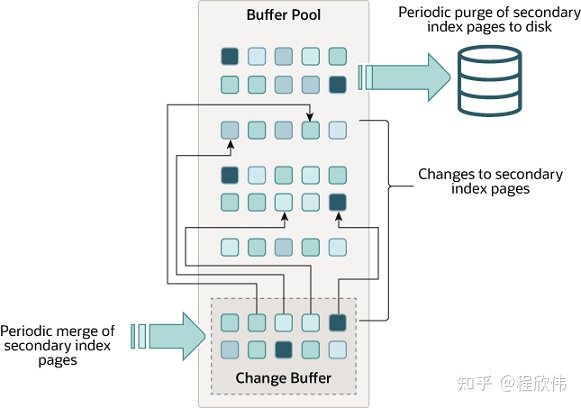
mysql 内存架构
1. 背景 从 innodb 的整体架构中可以知道 innodb 的内存架构中分为 buffer pool 缓存区, change pool 修改缓冲区, adaptive hash index 自适应哈希索引, 和 log buffer 日志缓冲区. 2. buffer pool buffer pool 是用于缓冲磁盘页的数据,mysql 的80%的内存会分配给…...
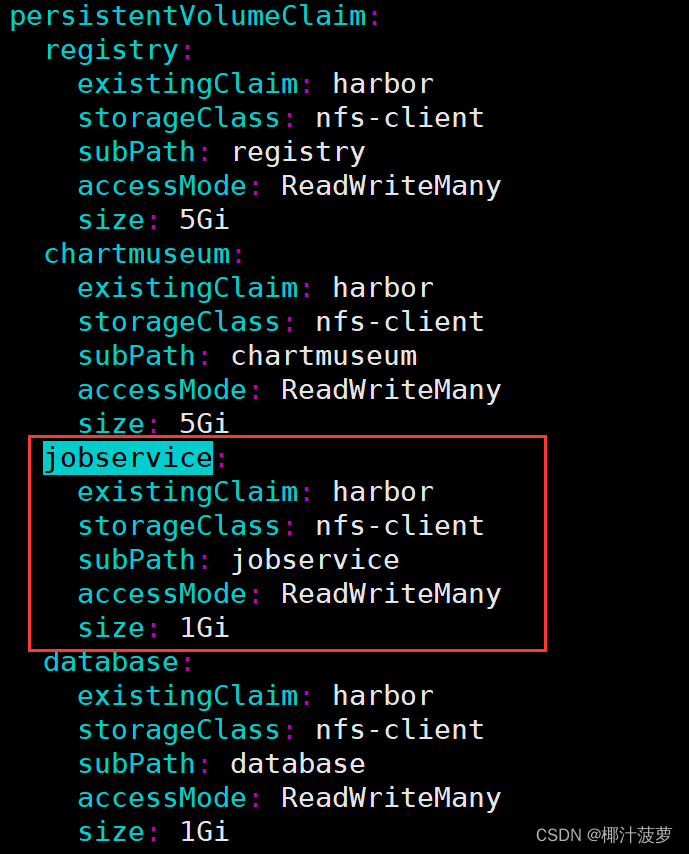
Helm安装Harbor
一、介绍 1.1 Harbor Harbor 是由 VMware 公司为企业用户设计的 Registry Server 开源项目,包括了权限管理 (RBAC)、LDAP、审计、管理界面、自我注册、HA 等企业必需的功能,同时针对中国用户的特点,设计镜像复制和中文支持等功能。目前该项…...

梯度下降优化器:SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam -> AdamW
目录 1 前言 2 梯度概念 3 一般梯度下降法 4 BGD 5 SGD 6 MBGD 7 Momentum 8 SGDM(SGD with momentum) 9 NAG(Nesterov Accelerated Gradient) 10 AdaGrad 11 RMSProp 12 Adadelta 13 Adam 13 Nadam 14 AdamW 15 Lion(EvoLve…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...
