【AI】深度学习——前馈神经网络——全连接前馈神经网络
文章目录
- 1.1 全连接前馈神经网络
- 1.1.1 符号说明
- 超参数
- 参数
- 活性值
- 1.1.2 信息传播公式
- 通用近似定理
- 1.1.3 神经网络与机器学习结合
- 二分类问题
- 多分类问题
- 1.1.4 参数学习
- 矩阵求导
- 链式法则
- 更为高效的参数学习
- 反向传播算法
- 自动梯度计算
- 数值微分
- 符号微分
- 自动微分
- 自动微分与符号微分区别
- 优化问题
- 非凸优化问题
- 梯度消失问题
- 1.1.5 全连接的前馈神经网络问题
- 参数太多
- 局部不变性
1.1 全连接前馈神经网络
前馈神经网络(Feedforward Neural Network,FNN)也称为多层感知器(实际上前馈神经网络由多层Logistic回归模型组成)
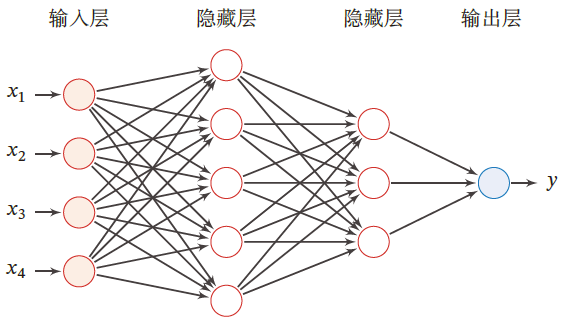
前馈神经网络中,各个神经元属于不同的层
每层神经元接收前一层神经元的信号,并输出到下一层
- 输入层:第0层
- 输出层:最后一层
- 隐藏层:其他中间层
整个网络中无反馈,信号从输入层向输出层单向传播,可用一个有向无环图表示
1.1.1 符号说明
超参数
| 符号 | 含义 |
|---|---|
| L L L | 神经网络层数 |
| M l M_l Ml | 第 l l l 层神经元个数 |
| f l ( ⋅ ) f_l(\cdot) fl(⋅) | 第 l l l 层神经元的激活函数 |
参数
| 符号 | 含义 |
|---|---|
| W ( l ) ∈ R M l × M l − 1 W^{(l)}\in \R^{M_l\times M_{l-1}} W(l)∈RMl×Ml−1 | 第 l − 1 l-1 l−1 层到第 l l l 层的权重矩阵 |
| b ( l ) ∈ R M l × M l − 1 b^{(l)}\in \R^{M_l\times M_{l-1}} b(l)∈RMl×Ml−1 | 第 l − 1 l-1 l−1 层到第 l l l 层的偏置 |
活性值
| 符号 | 含义 |
|---|---|
| z ( l ) ∈ R M l z^{(l)}\in\R^{M_l} z(l)∈RMl | 第 l l l 层神经元的净输入(净活性值) |
| a ( l ) ∈ R M l a^{(l)}\in \R^{M_{l}} a(l)∈RMl | 第 l l l 层神经元的输出(活性值) |
1.1.2 信息传播公式
神经网络的第 l l l 层有 M l M_l Ml 个神经元,相应的有 M l M_l Ml 个净输入和活性值,所以二者需要由 R M l \R^{M_l} RMl 向量来表示
第 l l l 层的输入为第 l − 1 l-1 l−1 层的活性值,相应的为 R M l − 1 \R^{M_{l-1}} RMl−1 向量,即 z ( l − 1 ) , a ( l − 1 ) ∈ R M l − 1 z^{(l-1)},a^{(l-1)}\in \R^{M_{l-1}} z(l−1),a(l−1)∈RMl−1
故第 l l l 层神经元的净输入需要经过一个 仿射变换,即
z ( l ) = W ( l ) a ( l − 1 ) + b ( l ) ,其中 W ( l ) ∈ R M l × M l − 1 = W ( l − 1 ) f l − 1 ( z ( l − 1 ) ) + b ( l ) \begin{aligned} z^{(l)}&=W^{(l)}a^{(l-1)}+b^{(l)},其中 W^{(l)}\in \R^{M_l\times M_{l-1}}\\ &=W^{(l-1)}f_{l-1}(z^{(l-1)})+b^{(l)} \end{aligned} z(l)=W(l)a(l−1)+b(l),其中W(l)∈RMl×Ml−1=W(l−1)fl−1(z(l−1))+b(l)
活性值 a ( l ) a^{(l)} a(l) 需要经过一个 非线性变换
a ( l ) = f l ( z ( l ) ) = f l ( W ( l ) a ( l − 1 ) + b ( l ) ) \begin{aligned} a^{(l)}&=f_l(z^{(l)})\\ &=f_l(W^{(l)}a^{(l-1)}+b^{(l)}) \end{aligned} a(l)=fl(z(l))=fl(W(l)a(l−1)+b(l))
进而可知,由输入到网络最后的输出 a ( L ) a^{(L)} a(L)
x = a ( 0 ) → W 1 z ( 1 ) → f 1 ( ) a ( 1 ) ⋯ → f L − 1 ( ) a ( L − 1 ) → W L z ( L ) → f L ( ) a ( L ) = ϕ ( x ; W ; b ) x=a^{(0)}\xrightarrow{W_1}z^{(1)}\xrightarrow{f_1()}a^{(1)}\cdots\xrightarrow{f_{L-1}()}a^{(L-1)}\xrightarrow{W_{L}}z^{(L)}\xrightarrow{f_L()}a^{(L)}=\phi(x;W;b) x=a(0)W1z(1)f1()a(1)⋯fL−1()a(L−1)WLz(L)fL()a(L)=ϕ(x;W;b)
其中 W , b W,b W,b 表示网络中所有层的连接权重和偏置
前馈神经网络可以通过逐层的信息传递,整个网络可以看做一个复合函数 ϕ ( x ; W ; b ) \phi(x;W;b) ϕ(x;W;b)
通用近似定理

根据通用近似定理,对于具有 线性输出层 z ( l ) z^{(l)} z(l) 和至少一个 具有挤压性质的激活函数 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅) 的隐藏层组成的前馈神经网络,只要隐藏层的神经元数量足够,就可以以任意精度来近似任何一个定义在实数空间中的有界闭函数
1.1.3 神经网络与机器学习结合
神经网络可以作为一个万能函数,用于进行复杂的特征转换或逼近一个条件分布
在机器学习中,输入样本的特征对分类器性能的影响很大
若要获得很好的分类效果,需要将样本的原始特征向量 x x x 转换到更有效的特征向量 ϕ ( x ) \phi(x) ϕ(x) ——特征抽取
多层前馈神经网络恰好可以看做一个非线性函数 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅) ,将输入 x ∈ R D x\in \R^D x∈RD 映射到输出 ϕ ( x ) ∈ R D ′ \phi(x)\in \R^{D'} ϕ(x)∈RD′ ,因此可将多层前馈神经网络看作一种特殊的特征转换方法,其输出 ϕ ( x ) \phi(x) ϕ(x) 作为分类器的输入
y ^ = g ( ϕ ( x ) ; θ ) \hat{y}=g(\phi(x);\theta) y^=g(ϕ(x);θ)
- g ( ⋅ ) g(\cdot) g(⋅) 为线性或非线性分类器
- θ \theta θ 为分类器 g ( ⋅ ) g(\cdot) g(⋅) 的参数
- y ^ \hat{y} y^ 为分类器输出
若分类器 g ( ⋅ ) g(\cdot) g(⋅) 为 L o g i s t i c 回归 Logistic回归 Logistic回归 或 S o f t m a x 回归 Softmax回归 Softmax回归 ,则相当于在输出层引入分类器,神经网络直接输出在不同类别的条件概率 p ( y ∣ x ) p(y\vert x) p(y∣x)
二分类问题
对于二分类问题 y ∈ { 0 , 1 } y\in \{0,1\} y∈{0,1} ,且采用 L o g i s t i c 回归 Logistic回归 Logistic回归 ,那么 L o g i s t i c Logistic Logistic 相当与神经网络的输出层,只需要一个神经元,其激活函数就是 L o g i s t i c 函数 Logistic函数 Logistic函数 ,可直接作为类别 y = 1 y=1 y=1 的条件概率
p ( y = 1 ∣ x ) = a ( L ) ∈ R p(y=1\vert x)=a^{(L)}\in \R p(y=1∣x)=a(L)∈R
多分类问题
对于多分类问题 y ∈ { 1 , ⋯ , C } y\in \{1,\cdots,C\} y∈{1,⋯,C} ,如果使用 S o f t m a x 回归 Softmax回归 Softmax回归 ,相当于网络最后一层设置 C C C 个神经元,其激活函数为 S o f t m a x 函数 Softmax函数 Softmax函数 ,网络最后一层的输出可以作为每个类的条件概率
y ^ = s o f t m a x ( z ( l ) ) \hat{y}=softmax(z^{(l)}) y^=softmax(z(l))
其中, z ( L ) ∈ R C z^{(L)}\in \R^C z(L)∈RC 为第 L L L 层神经元的净输入
y ^ ∈ R C \hat{y}\in\R^C y^∈RC 为第 L L L 层神经元的活性值,每一维分别表示不同类别标签的预测条件概率
1.1.4 参数学习
如果采用交叉熵损失函数,对于样本 ( x , y ) (x,y) (x,y) ,其损失函数为
L ( y , y ^ ) = − y log y ^ , y ∈ { 0 , 1 } C \mathcal{L}(y,\hat{y})=-y\log \hat{y},y\in \{0,1\}^C L(y,y^)=−ylogy^,y∈{0,1}C
给定训练集 D = { ( x i , y i ) } i = 1 N \mathcal{D}=\{(x_i,y_i)\}_{i=1}^N D={(xi,yi)}i=1N ,将每个样本 x i x_i xi 输入给前馈网络得到 y ^ i \hat{y}_i y^i ,其结构化风险函数为
R ( W , b ) = 1 N ∑ i = 1 N L ( y i , y ^ i ) + 1 2 λ ∥ W ∥ F 2 \mathcal{R}(W,b)=\frac{1}{N}\sum\limits_{i=1}^N\mathcal{L}(y_i,\hat{y}_i)+\frac{1}{2}\lambda\Vert W\Vert_F^2 R(W,b)=N1i=1∑NL(yi,y^i)+21λ∥W∥F2
-
λ \lambda λ 为超参数, λ \lambda λ 越大, W W W 越接近于0
-
一般用 F r o b e n i u s Frobenius Frobenius 范数(F范数)作为惩罚项
∥ W ∥ F 2 = ∑ l = 1 L ∑ i = 1 M l ∑ j = 1 M l − 1 ( ω i j ( l ) ) 2 \Vert W\Vert_F^2=\sum\limits_{l=1}^L\sum\limits_{i=1}^{M_l}\sum\limits_{j=1}^{M_{l-1}}\left(\omega_{ij}^{(l)}\right)^2 ∥W∥F2=l=1∑Li=1∑Mlj=1∑Ml−1(ωij(l))2
对于网络参数,可以通过梯度下降的方法学习
W ( l ) ← W ( l ) − α ∂ R ( W , b ) ∂ W ( l ) ← W ( l ) − α ( 1 N ∑ i = 1 N ∂ L ( y i , y ^ i ) ∂ W ( l ) + λ W ( l ) ) b ( l ) ← b ( l ) − α ∂ R ( W , b ) ∂ b ( l ) ← b ( l ) − α ( 1 N ∑ i = 1 N ∂ L ( y i , y ^ i ) ∂ b ( l ) ) \begin{aligned} W^{(l)}&\leftarrow W^{(l)}-\alpha\frac{\partial \mathcal{R}(W,b)}{\partial W^{(l)}}\\ &\leftarrow W^{(l)}-\alpha\left(\frac{1}{N}\sum\limits_{i=1}^N\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial W^{(l)}}+\lambda W^{(l)}\right)\\ b^{(l)}&\leftarrow b^{(l)}-\alpha\frac{\partial \mathcal{R}(W,b)}{\partial b^{(l)}}\\ &\leftarrow b^{(l)}-\alpha\left(\frac{1}{N}\sum\limits_{i=1}^N\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial b^{(l)}}\right) \end{aligned} W(l)b(l)←W(l)−α∂W(l)∂R(W,b)←W(l)−α(N1i=1∑N∂W(l)∂L(yi,y^i)+λW(l))←b(l)−α∂b(l)∂R(W,b)←b(l)−α(N1i=1∑N∂b(l)∂L(yi,y^i))
矩阵求导
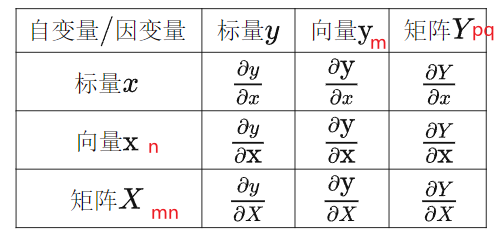
根据求导的自变量和因变量是标量, 列向量 列向量 列向量 还是矩阵 ,我们有9种可能的矩阵求导定义:
含标量情况:
- ∂ 标量 ∂ 标量 = 标量 \frac{\partial 标量}{\partial 标量}=标量 ∂标量∂标量=标量
- ∂ 标量 ∂ 向量 = 向量 \frac{\partial 标量}{\partial 向量}=向量 ∂向量∂标量=向量 , ∂ 标量 ∂ 矩阵 = 矩阵 \frac{\partial 标量}{\partial 矩阵}=矩阵 ∂矩阵∂标量=矩阵
- ∂ 向量 ∂ 标量 = 向量 \frac{\partial 向量}{\partial 标量}=向量 ∂标量∂向量=向量 , ∂ 矩阵 ∂ 标量 = 矩阵 \frac{\partial 矩阵}{\partial 标量}=矩阵 ∂标量∂矩阵=矩阵
标量情况,第2种和第3种情况,引出信息的两种布局方式
- 分子布局:结果的行维度与分子行维度相同
- 分母布局:结果的行维度与分母行维度相同
不论是向量也好,矩阵也好,对向量求导也好,对矩阵求导也好,结果都可以转化成标量之间的求导,最后把结果按照一定的方式拼接起来,以向量或者矩阵的形式表达出来。
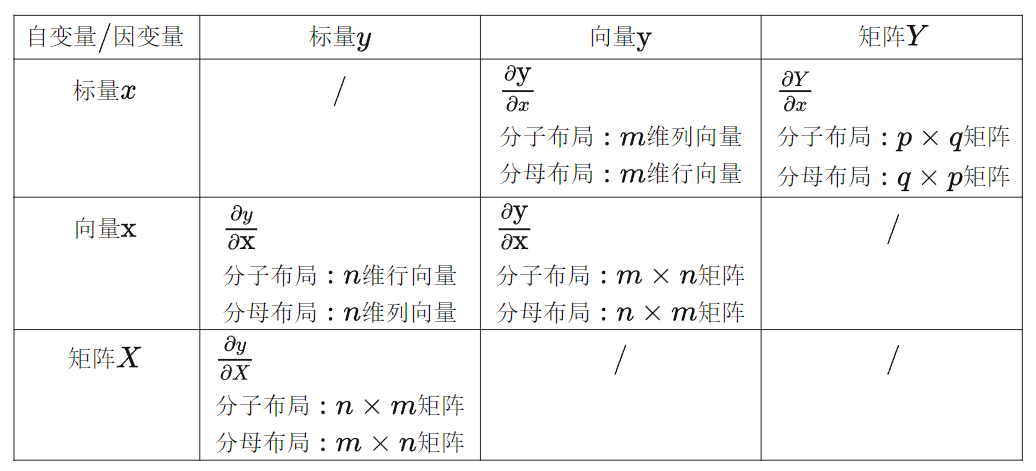
分子布局和分母布局的结果相差一个转置
在机器学习的算法推导中,通常遵循以下布局规则:
- 如果向量或矩阵对标量求导,则以分子布局为主
- 如果标量对向量或矩阵求导,则以分母布局为主
- 向量对向量求导,有些分歧,一般以分子布局的雅克比矩阵为主。
本文沿用nndl的思路,以分母布局为主
若 x ( i ) ∈ R x^{(i)}\in \R x(i)∈R ,向量 x = [ x ( 1 ) x ( 2 ) ⋮ x ( M ) ] ∈ R M × 1 x=\left[\begin{matrix}x^{(1)}\\x^{(2)}\\\vdots\\x^{(M)}\end{matrix}\right]\in \R^{M\times 1} x= x(1)x(2)⋮x(M) ∈RM×1
-
若 y = g ( x ) ∈ R 1 × 1 y=g(x)\in\R^{1\times 1} y=g(x)∈R1×1 ,则
∂ y ∂ x = [ ∂ y ∂ x ( 1 ) ∂ y ∂ x ( 2 ) ⋮ ∂ y ∂ x ( M ) ] ∈ R M × 1 \frac{\partial y}{\partial x}=\left[\begin{matrix} \frac{\partial y}{\partial x^{(1)}}\\ \frac{\partial y}{\partial x^{(2)}}\\ \vdots\\ \frac{\partial y}{\partial x^{(M)}} \end{matrix} \right]\in \R^{M\times 1} ∂x∂y= ∂x(1)∂y∂x(2)∂y⋮∂x(M)∂y ∈RM×1 -
若 y i = g i ( x ) y_i=g_i(x) yi=gi(x) , y = [ y 1 y 2 ⋮ y N ] ∈ R N × 1 y=\left[\begin{matrix}y_1\\y_2\\\vdots\\y_N\end{matrix}\right]\in \R^{N\times 1} y= y1y2⋮yN ∈RN×1 ,则
∂ y ∂ x = [ ∂ y 1 ∂ x , ∂ y 2 ∂ x , ⋯ , ∂ y N ∂ x ] = [ ∂ y 1 ∂ x 1 ∂ y 2 ∂ x 1 ⋯ ∂ y N ∂ x 1 ∂ y 1 ∂ x 2 ∂ y 2 ∂ x 2 ⋯ ∂ y N ∂ x 2 ⋮ ⋮ ⋱ ⋮ ∂ y 1 ∂ x M ∂ y 2 ∂ x M ⋯ ∂ y N ∂ x M ] ∈ R M × N \frac{\partial y}{\partial x}=\left[ \begin{matrix} \frac{\partial y_1}{\partial x},\frac{\partial y_2}{\partial x},\cdots,\frac{\partial y_N}{\partial x} \end{matrix} \right]=\left[ \begin{matrix} \frac{\partial y_1}{\partial x_1}&\frac{\partial y_2}{\partial x_1}&\cdots&\frac{\partial y_N}{\partial x_1}\\ \frac{\partial y_1}{\partial x_2}&\frac{\partial y_2}{\partial x_2}&\cdots&\frac{\partial y_N}{\partial x_2}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial y_1}{\partial x_M}&\frac{\partial y_2}{\partial x_M}&\cdots&\frac{\partial y_N}{\partial x_M}\\ \end{matrix} \right]\in \R^{M\times N} ∂x∂y=[∂x∂y1,∂x∂y2,⋯,∂x∂yN]= ∂x1∂y1∂x2∂y1⋮∂xM∂y1∂x1∂y2∂x2∂y2⋮∂xM∂y2⋯⋯⋱⋯∂x1∂yN∂x2∂yN⋮∂xM∂yN ∈RM×N
链式法则
y = f 5 ( f 4 ( f 3 ( f 2 ( f 1 ( x ) ) ) ) ) → ∂ y ∂ x = ∂ f 5 ∂ f 4 ∂ f 4 ∂ f 3 ∂ f 3 ∂ f 2 ∂ f 2 ∂ f 1 ∂ f 1 ∂ x y=f_5(f_4(f_3(f_2(f_1(x)))))\rightarrow \frac{\partial y}{\partial x}=\frac{\partial f_5}{\partial f_4}\frac{\partial f_4}{\partial f_3}\frac{\partial f_3}{\partial f_2}\frac{\partial f_2}{\partial f_1}\frac{\partial f_1}{\partial x} y=f5(f4(f3(f2(f1(x)))))→∂x∂y=∂f4∂f5∂f3∂f4∂f2∂f3∂f1∂f2∂x∂f1
若 x ∈ R x\in \R x∈R,
{ y i = g i ( x ) y = [ g 1 ( x ) , g 2 ( x ) , ⋯ , g M ( x ) ] ∈ R M z i = f i ( y ) z = [ f 1 ( y ) , f 2 ( y ) , ⋯ , f N ( y ) ] ∈ R N \begin{cases} y_i=g_i(x)&y=[g_1(x),g_2(x),\cdots,g_M(x)]\in \R^{M}\\ z_i=f_i(y)&z=\left[f_1(y),f_2(y),\cdots,f_N(y)\right]\in \R^{N} \end{cases} {yi=gi(x)zi=fi(y)y=[g1(x),g2(x),⋯,gM(x)]∈RMz=[f1(y),f2(y),⋯,fN(y)]∈RN
则有
∂ z ∂ x = ∂ y ∂ x 1 × M ∂ z ∂ y M × N ∈ R 1 × N \frac{\partial z}{\partial x}=\frac{\partial y}{\partial x}_{1\times M}\frac{\partial z}{\partial y}_{M\times N}\in\R^{1\times N} ∂x∂z=∂x∂y1×M∂y∂zM×N∈R1×N
若 x ∈ R M x\in \R^{M} x∈RM
{ y i = g i ( x ) y = [ g 1 ( x ) , g 2 ( x ) , ⋯ , g K ( x ) ] ∈ R K z i = f i ( y ) z = [ f 1 ( y ) , f 2 ( y ) , ⋯ , f N ( y ) ] ∈ R N \begin{cases} y_i=g_i(x)&y=[g_1(x),g_2(x),\cdots,g_K(x)]\in \R^{K}\\ z_i=f_i(y)&z=\left[f_1(y),f_2(y),\cdots,f_N(y)\right]\in \R^{N} \end{cases} {yi=gi(x)zi=fi(y)y=[g1(x),g2(x),⋯,gK(x)]∈RKz=[f1(y),f2(y),⋯,fN(y)]∈RN
则有
∂ z ∂ x = ∂ y ∂ x M × K ∂ z ∂ y K × N ∈ R M × N \frac{\partial z}{\partial x}=\frac{\partial y}{\partial x}_{M\times K}\frac{\partial z}{\partial y}_{K\times N}\in \R^{M\times N} ∂x∂z=∂x∂yM×K∂y∂zK×N∈RM×N
若 X ∈ R M × N X\in R^{M\times N} X∈RM×N ,
{ y i = g i ( X ) y = [ g 1 ( X ) , g 2 ( X ) , ⋯ , g K ( X ) ] ∈ R K z i = f ( y ) ∈ R \begin{cases} y_i=g_i(X)&y=[g_1(X),g_2(X),\cdots,g_K(X)]\in \R^{K}\\ z_i=f(y)\in \R \end{cases} {yi=gi(X)zi=f(y)∈Ry=[g1(X),g2(X),⋯,gK(X)]∈RK
则有
∂ z ∂ x i j = ∂ y ∂ x i j 1 × K ∂ z ∂ y K × 1 ∈ R \frac{\partial z}{\partial x_{ij}}=\frac{\partial y}{\partial x_{ij}}_{1\times K}\frac{\partial z}{\partial y}_{K\times 1}\in \R ∂xij∂z=∂xij∂y1×K∂y∂zK×1∈R
更为高效的参数学习
梯度下降法需要计算损失函数对参数的偏导数,如果通过链式法则逐一对每个参数求偏导,会很低效
- 反向传播算法
- 自动梯度计算
反向传播算法
目标
求解
W ( l ) ← W ( l ) − α ∂ R ( W , b ) ∂ W ( l ) ← W ( l ) − α ( 1 N ∑ i = 1 N ∂ L ( y i , y ^ i ) ∂ W ( l ) + λ W ( l ) ) b ( l ) ← b ( l ) − α ∂ R ( W , b ) ∂ b ( l ) ← b ( l ) − α ( 1 N ∑ i = 1 N ∂ L ( y i , y ^ i ) ∂ b ( l ) ) \begin{aligned} W^{(l)}&\leftarrow W^{(l)}-\alpha\frac{\partial \mathcal{R}(W,b)}{\partial W^{(l)}}\\ &\leftarrow W^{(l)}-\alpha\left(\frac{1}{N}\sum\limits_{i=1}^N\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial W^{(l)}}+\lambda W^{(l)}\right)\\ b^{(l)}&\leftarrow b^{(l)}-\alpha\frac{\partial \mathcal{R}(W,b)}{\partial b^{(l)}}\\ &\leftarrow b^{(l)}-\alpha\left(\frac{1}{N}\sum\limits_{i=1}^N\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial b^{(l)}}\right) \end{aligned} W(l)b(l)←W(l)−α∂W(l)∂R(W,b)←W(l)−α(N1i=1∑N∂W(l)∂L(yi,y^i)+λW(l))←b(l)−α∂b(l)∂R(W,b)←b(l)−α(N1i=1∑N∂b(l)∂L(yi,y^i))
可见参数求解的核心部分为 ∂ L ( y i , y ^ i ) ∂ W ( l ) \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial W^{(l)}} ∂W(l)∂L(yi,y^i) ,对于矩阵求导,可以对逐个元素求导,再排列为矩阵形式,根据链式法则
∂ L ( y i , y ^ i ) ∂ w i j ( l ) = ∂ z ( l ) ∂ w i j ( l ) ∂ L ( y i , y ^ i ) ∂ z ( l ) ∂ L ( y i , y ^ i ) ∂ b ( l ) = ∂ z ( l ) ∂ b ( l ) ∂ L ( y i , y ^ i ) ∂ z ( l ) \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial w_{ij}^{(l)}}=\frac{\partial z^{(l)}}{\partial w^{(l)}_{ij}}\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z^{(l)}}\\ \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial b^{(l)}}=\frac{\partial z^{(l)}}{\partial b^{(l)}}\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z^{(l)}} ∂wij(l)∂L(yi,y^i)=∂wij(l)∂z(l)∂z(l)∂L(yi,y^i)∂b(l)∂L(yi,y^i)=∂b(l)∂z(l)∂z(l)∂L(yi,y^i)
计算 ∂ z ( l ) ∂ w i j ( l ) \frac{\partial z^{(l)}}{\partial w^{(l)}_{ij}} ∂wij(l)∂z(l)
因 z M l × 1 ( l ) = W M l × M l − 1 ( l ) a M l − 1 × 1 ( l − 1 ) + b M l ( l ) z^{(l)}_{M_l\times 1}=W^{(l)}_{M_{l}\times M_{l-1}}a^{(l-1)}_{M_{l-1}\times 1}+b^{(l)}_{M_{l}} zMl×1(l)=WMl×Ml−1(l)aMl−1×1(l−1)+bMl(l)

- 分母布局,故需要将 z ( l ) z^{(l)} z(l) 转置求偏导,第 i i i 个元素为 a j ( l − 1 ) a_j^{(l-1)} aj(l−1)
计算 ∂ z ( l ) ∂ b ( l ) \frac{\partial z^{(l)}}{\partial b^{(l)}} ∂b(l)∂z(l)

计算 ∂ L ( y i , y ^ i ) ∂ z ( l ) \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z^{(l)}} ∂z(l)∂L(yi,y^i)
计算误差项 ∂ L ( y i , y ^ i ) ∂ z ( l ) \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z^{(l)}} ∂z(l)∂L(yi,y^i) 表示第 l l l 层神经元对最终损失的影响,也反映了最终损失对第 l l l 层神经元的敏感程度,不同神经元对网络能力的贡献程度,从而比较好地解决了贡献度分配问题
δ ( l ) = Δ ∂ L ( y i , y ^ i ) ∂ z ( l ) = [ ∂ L ( y i , y ^ i ) ∂ z 1 ( l ) ∂ L ( y i , y ^ i ) ∂ z 2 ( l ) ⋮ ∂ L ( y i , y ^ i ) ∂ z M l ( l ) ] = Δ [ δ 1 ( l ) δ 2 ( l ) ⋮ δ M l ( l ) ] ∈ R M l × 1 \delta^{(l)}\overset{\Delta}{=}\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z^{(l)}}=\left[ \begin{matrix} \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z_1^{(l)}}\\ \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z_2^{(l)}}\\ \vdots\\ \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial z_{M_l}^{(l)}} \end{matrix} \right]\overset{\Delta}{=}\left[ \begin{matrix} \delta_1^{(l)}\\ \delta_2^{(l)}\\ \vdots\\ \delta_{M_l}^{(l)} \end{matrix} \right]\in \R^{M_l\times 1} δ(l)=Δ∂z(l)∂L(yi,y^i)= ∂z1(l)∂L(yi,y^i)∂z2(l)∂L(yi,y^i)⋮∂zMl(l)∂L(yi,y^i) =Δ δ1(l)δ2(l)⋮δMl(l) ∈RMl×1
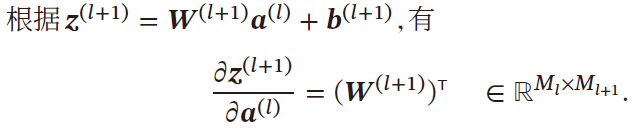
- z ( l + 1 ) ∈ R M l + 1 z^{(l+1)}\in \R^{M_{l+1}} z(l+1)∈RMl+1 , a ( l ) ∈ R M l a^{(l)}\in \R^{M_l} a(l)∈RMl ,所以
z ( l + 1 ) a ( l ) = 分母布局 [ w 11 w 21 ⋯ w M l + 1 1 w 12 w 22 ⋯ w M l + 1 2 ⋮ ⋮ ⋱ ⋮ w 1 M l w 2 M l ⋯ w M l + 1 M l ] ∈ R M l × M l + 1 \frac{z^{(l+1)}}{a^{(l)}}\xlongequal{分母布局}\left[ \begin{matrix} w_{11}&w_{21}&\cdots &w_{M_{l+1}1}\\ w_{12}&w_{22}&\cdots &w_{M_{l+1}2}\\ \vdots&\vdots&\ddots&\vdots\\ w_{1M_l}&w_{2M_l}&\cdots &w_{M_{l+1}M_l}\\ \end{matrix} \right]\in \R^{M_l\times M_{l+1}} a(l)z(l+1)分母布局 w11w12⋮w1Mlw21w22⋮w2Ml⋯⋯⋱⋯wMl+11wMl+12⋮wMl+1Ml ∈RMl×Ml+1
根据 a ( l ) = f l ( z ( l ) ) = ( f l ( z 1 ( l ) ) f l ( z 2 ( l ) ) ⋮ f l ( z M l ( l ) ) ) a^{(l)}=f_l(z^{(l)})=\left(\begin{matrix}f_l(z_1^{(l)})\\f_l(z_2^{(l)})\\\vdots\\f_l(z_{M_l}^{(l)})\\\end{matrix}\right) a(l)=fl(z(l))= fl(z1(l))fl(z2(l))⋮fl(zMl(l)) , z ( l ) = ( z 1 ( l ) z 2 ( l ) ⋮ z M l ( l ) ) z^{(l)}=\left(\begin{matrix}z_1^{(l)}\\z^{(l)}_2\\\vdots\\z_{M_l}^{(l)}\end{matrix}\right) z(l)= z1(l)z2(l)⋮zMl(l) ,分母布局
∂ a ( l ) ∂ z ( l ) = ∂ f l ( z ( l ) ) ∂ z ( l ) = [ ∂ f l ( z 1 ( l ) ) ∂ z 1 ( l ) ∂ f l ( z 2 ( l ) ) ∂ z 1 ( l ) ⋯ ∂ f l ( z M l ( l ) ) ∂ z 1 ( l ) ∂ f l ( z 1 ( l ) ) ∂ z 2 ( l ) ∂ f l ( z 2 ( l ) ) ∂ z 2 ( l ) ⋯ ∂ f l ( z M l ( l ) ) ∂ z 2 ( l ) ⋮ ⋮ ⋱ ⋮ ∂ f l ( z 1 ( l ) ) ∂ z M l ∂ f l ( z 2 ( l ) ) ∂ z M l ( l ) ⋯ ∂ f l ( z M l ( l ) ) ∂ z M l ( l ) ] = [ ∂ f l ( z 1 ( l ) ) ∂ z 1 ( l ) 0 ⋯ 0 0 ∂ f l ( z 2 ( l ) ) ∂ z 2 ( l ) ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ ∂ f l ( z M l ( l ) ) ∂ z M l ( l ) ] = d i a g ( ∂ f l ( z i ( l ) ) ∂ z i ( l ) ) ∈ R M l × M l , i = 1 , ⋯ , M l \begin{aligned} \frac{\partial a^{(l)}}{\partial z^{(l)}}&=\frac{\partial f_l(z^{(l)})}{\partial z^{(l)}}\\ &=\left[ \begin{matrix} \frac{\partial f_l(z_1^{(l)})}{\partial z_1^{(l)}}&\frac{\partial f_l(z_2^{(l)})}{\partial z_1^{(l)}}&\cdots&\frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{1}^{(l)}}\\ \frac{\partial f_l(z_1^{(l)})}{\partial z_2^{(l)}}&\frac{\partial f_l(z_2^{(l)})}{\partial z_2^{(l)}}&\cdots&\frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{2}^{(l)}}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial f_l(z_1^{(l)})}{\partial z_{M_l}}&\frac{\partial f_l(z_2^{(l)})}{\partial z_{M_l}^{(l)}}&\cdots&\frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{M_l}^{(l)}}\\ \end{matrix} \right]=\left[ \begin{matrix} \frac{\partial f_l(z_1^{(l)})}{\partial z_1^{(l)}}&0&\cdots&0\\ 0&\frac{\partial f_l(z_2^{(l)})}{\partial z_2^{(l)}}&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&\frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{M_l}^{(l)}}\\ \end{matrix} \right]\\ &=diag \left(\frac{\partial f_l(z^{(l)}_i)}{\partial z_i^{(l)}}\right)\in \R^{M_l\times M_l},i=1,\cdots,M_l \end{aligned} ∂z(l)∂a(l)=∂z(l)∂fl(z(l))= ∂z1(l)∂fl(z1(l))∂z2(l)∂fl(z1(l))⋮∂zMl∂fl(z1(l))∂z1(l)∂fl(z2(l))∂z2(l)∂fl(z2(l))⋮∂zMl(l)∂fl(z2(l))⋯⋯⋱⋯∂z1(l)∂fl(zMl(l))∂z2(l)∂fl(zMl(l))⋮∂zMl(l)∂fl(zMl(l)) = ∂z1(l)∂fl(z1(l))0⋮00∂z2(l)∂fl(z2(l))⋮0⋯⋯⋱⋯00⋮∂zMl(l)∂fl(zMl(l)) =diag(∂zi(l)∂fl(zi(l)))∈RMl×Ml,i=1,⋯,Ml

[ W ( l + 1 ) ] T ⋅ δ ( l + 1 ) = [ w 11 w 21 ⋯ w M l + 1 1 w 12 w 22 ⋯ w M l + 1 2 ⋮ ⋮ ⋱ ⋮ w 1 M l w 2 M l ⋯ w M l + 1 M l ] [ δ 1 ( l + 1 ) δ 2 ( l + 1 ) ⋮ δ M l + 1 ( l + 1 ) ] = [ ∑ t = 1 M l + 1 w t 1 δ t ( l + 1 ) ∑ t = 1 M l + 1 w t 2 δ t ( l + 1 ) ⋮ ∑ t = 1 M l + 1 w t M l + 1 δ t ( l + 1 ) ] ∈ R M l d i a g ( ∂ f l ( z i ( l ) ) ∂ z i ( l ) ) [ W ( l + 1 ) ] T ⋅ δ ( l + 1 ) = [ ∂ f l ( z 1 ( l ) ) ∂ z 1 ( l ) 0 ⋯ 0 0 ∂ f l ( z 2 ( l ) ) ∂ z 2 ( l ) ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ ∂ f l ( z M l ( l ) ) ∂ z M l ( l ) ] [ ∑ t = 1 M l + 1 w t 1 δ t ( l + 1 ) ∑ t = 1 M l + 1 w t 2 δ t ( l + 1 ) ⋮ ∑ t = 1 M l + 1 w t M l + 1 δ t ( l + 1 ) ] = [ ∂ f l ( z 1 ( l ) ) ∂ z 1 ( l ) ∑ t = 1 M l + 1 w t 1 δ t ( l + 1 ) ⋮ ∂ f l ( z i ( l ) ) ∂ z i ( l ) ∑ t = 1 M l + 1 w t i δ t ( l + 1 ) ⋮ ∂ f l ( z M l ( l ) ) ∂ z M l ( l ) ∑ t = 1 M l + 1 w t M l δ t ( l + 1 ) ] = Δ [ δ 1 ( l ) ⋮ δ i ( l ) ⋮ δ M l ( l ) ] \begin{aligned} \left[W^{(l+1)}\right]^T\cdot \delta^{(l+1)}&=\left[ \begin{matrix} w_{11}&w_{21}&\cdots &w_{M_{l+1}1}\\ w_{12}&w_{22}&\cdots &w_{M_{l+1}2}\\ \vdots&\vdots&\ddots&\vdots\\ w_{1M_l}&w_{2M_l}&\cdots &w_{M_{l+1}M_l}\\ \end{matrix} \right]\left[ \begin{matrix} \delta_1^{(l+1)}\\ \delta_2^{(l+1)}\\ \vdots\\ \delta_{M_{l+1}}^{(l+1)} \end{matrix} \right]\\ &=\left[ \begin{matrix} \sum\limits_{t=1}^{M_{l+1}}w_{t1}\delta_t^{(l+1)}\\ \sum\limits_{t=1}^{M_{l+1}}w_{t2}\delta_t^{(l+1)}\\ \vdots\\ \sum\limits_{t=1}^{M_{l+1}}w_{tM_{l+1}}\delta_t^{(l+1)}\\ \end{matrix} \right]\in\R^{M_l}\\ diag \left(\frac{\partial f_l(z^{(l)}_i)}{\partial z_i^{(l)}}\right)\left[W^{(l+1)}\right]^T\cdot \delta^{(l+1)}&=\left[ \begin{matrix} \frac{\partial f_l(z_1^{(l)})}{\partial z_1^{(l)}}&0&\cdots&0\\ 0&\frac{\partial f_l(z_2^{(l)})}{\partial z_2^{(l)}}&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&\frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{M_l}^{(l)}}\\ \end{matrix} \right]\left[ \begin{matrix} \sum\limits_{t=1}^{M_{l+1}}w_{t1}\delta_t^{(l+1)}\\ \sum\limits_{t=1}^{M_{l+1}}w_{t2}\delta_t^{(l+1)}\\ \vdots\\ \sum\limits_{t=1}^{M_{l+1}}w_{tM_{l+1}}\delta_t^{(l+1)}\\ \end{matrix} \right]\\ &=\left[\begin{matrix} \frac{\partial f_l(z_1^{(l)})}{\partial z_1^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{t1}\delta_t^{(l+1)}\\ \vdots\\ \frac{\partial f_l(z_i^{(l)})}{\partial z_i^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{ti}\delta_t^{(l+1)}\\ \vdots\\ \frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{M_l}^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{tM_{l}}\delta_t^{(l+1)} \end{matrix} \right]\overset{\Delta}{=}\left[\begin{matrix} \delta^{(l)}_1\\ \vdots\\ \delta^{(l)}_i\\ \vdots\\ \delta^{(l)}_{M_l}\\ \end{matrix} \right] \end{aligned} [W(l+1)]T⋅δ(l+1)diag(∂zi(l)∂fl(zi(l)))[W(l+1)]T⋅δ(l+1)= w11w12⋮w1Mlw21w22⋮w2Ml⋯⋯⋱⋯wMl+11wMl+12⋮wMl+1Ml δ1(l+1)δ2(l+1)⋮δMl+1(l+1) = t=1∑Ml+1wt1δt(l+1)t=1∑Ml+1wt2δt(l+1)⋮t=1∑Ml+1wtMl+1δt(l+1) ∈RMl= ∂z1(l)∂fl(z1(l))0⋮00∂z2(l)∂fl(z2(l))⋮0⋯⋯⋱⋯00⋮∂zMl(l)∂fl(zMl(l)) t=1∑Ml+1wt1δt(l+1)t=1∑Ml+1wt2δt(l+1)⋮t=1∑Ml+1wtMl+1δt(l+1) = ∂z1(l)∂fl(z1(l))t=1∑Ml+1wt1δt(l+1)⋮∂zi(l)∂fl(zi(l))t=1∑Ml+1wtiδt(l+1)⋮∂zMl(l)∂fl(zMl(l))t=1∑Ml+1wtMlδt(l+1) =Δ δ1(l)⋮δi(l)⋮δMl(l)
合并求梯度
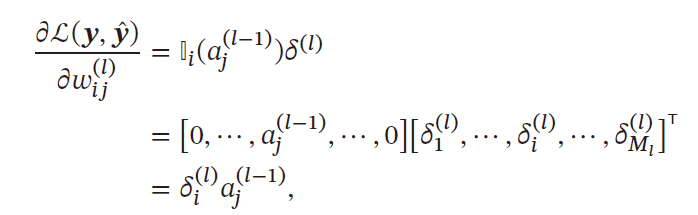
∂ L ( y i , y ^ i ) ∂ w i j ( l ) = [ 0 , ⋯ , a j ( l − 1 ) , ⋯ 0 ] [ δ 1 ( l ) ⋮ δ i ( l ) ⋮ δ M l ( l ) ] = a j ( l − 1 ) δ i ( l ) = a j ( l − 1 ) ∂ f l ( z i ( l ) ) ∂ z i ( l ) ∑ t = 1 M l + 1 w t i δ t ( l + 1 ) ⟺ [ δ ( l ) ⋅ a ( l − 1 ) ] i j 即 [ ∂ L ( y i , y ^ i ) ∂ W ( l ) ] i j = [ δ ( l ) ⋅ a ( l − 1 ) ] i j \begin{aligned} \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial w_{ij}^{(l)}}&=\left[0,\cdots,a_j^{(l-1)},\cdots 0\right]\left[\begin{matrix} \delta^{(l)}_1\\ \vdots\\ \delta^{(l)}_i\\ \vdots\\ \delta^{(l)}_{M_l}\\ \end{matrix} \right]\\ &=a_j^{(l-1)}\delta^{(l)}_i=a^{(l-1)}_j\frac{\partial f_l(z_i^{(l)})}{\partial z_i^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{ti}\delta_t^{(l+1)}\\ &\iff \left[\delta^{(l)}\cdot a^{(l-1)}\right]_{ij}\\ 即\left[\frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial W^{(l)}}\right]_{ij}&=\left[\delta^{(l)}\cdot a^{(l-1)}\right]_{ij} \end{aligned} ∂wij(l)∂L(yi,y^i)即[∂W(l)∂L(yi,y^i)]ij=[0,⋯,aj(l−1),⋯0] δ1(l)⋮δi(l)⋮δMl(l) =aj(l−1)δi(l)=aj(l−1)∂zi(l)∂fl(zi(l))t=1∑Ml+1wtiδt(l+1)⟺[δ(l)⋅a(l−1)]ij=[δ(l)⋅a(l−1)]ij
故梯度 ∂ L ( y i , y ^ i ) ∂ W ( l ) \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial W^{(l)}} ∂W(l)∂L(yi,y^i) 关于第 l l l 层权重 W ( l ) W^{(l)} W(l) 的梯度为
∂ L ( y i , y ^ i ) ∂ W ( l ) = δ ( l ) ⋅ a ( l − 1 ) ∈ R M l × M l − 1 \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial W^{(l)}}=\delta^{(l)}\cdot a^{(l-1)}\in \R^{M_l\times M_{l-1}} ∂W(l)∂L(yi,y^i)=δ(l)⋅a(l−1)∈RMl×Ml−1
同理, L ( y , y ^ ) \mathcal{L}(y,\hat{y}) L(y,y^) 关于第 l l l 层偏置 b ( l ) b^{(l)} b(l) 的梯度为
∂ L ( y i , y ^ i ) ∂ b ( l ) = δ ( l ) ∈ R M l \frac{\partial \mathcal{L}(y_i,\hat{y}_i)}{\partial b^{(l)}}=\delta^{(l)}\in \R^{M_l} ∂b(l)∂L(yi,y^i)=δ(l)∈RMl
其中
δ ( l ) = [ ∂ f l ( z 1 ( l ) ) ∂ z 1 ( l ) ∑ t = 1 M l + 1 w t 1 δ t ( l + 1 ) ⋮ ∂ f l ( z i ( l ) ) ∂ z i ( l ) ∑ t = 1 M l + 1 w t i δ t ( l + 1 ) ⋮ ∂ f l ( z M l ( l ) ) ∂ z M l ( l ) ∑ t = 1 M l + 1 w t M l δ t ( l + 1 ) ] = f l ′ ( z ( l ) ) ⊙ [ ( W ( l + 1 ) ) T δ ( l + 1 ) ] \delta^{(l)}=\left[\begin{matrix} \frac{\partial f_l(z_1^{(l)})}{\partial z_1^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{t1}\delta_t^{(l+1)}\\ \vdots\\ \frac{\partial f_l(z_i^{(l)})}{\partial z_i^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{ti}\delta_t^{(l+1)}\\ \vdots\\ \frac{\partial f_l(z_{M_l}^{(l)})}{\partial z_{M_l}^{(l)}}\sum\limits_{t=1}^{M_{l+1}}w_{tM_{l}}\delta_t^{(l+1)} \end{matrix} \right]=f'_l(z^{(l)})\odot \left[\left(W^{(l+1)}\right)^T\delta^{(l+1)}\right] δ(l)= ∂z1(l)∂fl(z1(l))t=1∑Ml+1wt1δt(l+1)⋮∂zi(l)∂fl(zi(l))t=1∑Ml+1wtiδt(l+1)⋮∂zMl(l)∂fl(zMl(l))t=1∑Ml+1wtMlδt(l+1) =fl′(z(l))⊙[(W(l+1))Tδ(l+1)]
误差的反向传播
第 l l l 层的误差项可以通过第 l + 1 l+1 l+1 层的误差项计算得到,这就是 误差的反向传播
第 l l l 层的一个神经元的误差项是与该神经元相连的第 l + 1 l+1 l+1 层的神经元的误差项的权重和,然后,再乘上该神经元激活函数的梯度。
算法过程
在计算出每一层的误差项后,就可以求得本层的梯度,可以用随机梯度下降法来训练前馈神经网络
- 前馈计算每一层的净输入 z ( l ) z^{(l)} z(l) 和净激活值 a ( l ) a^{(l)} a(l) ,直至最后一层
- 反向传播计算每一层的误差项 δ ( l ) \delta^{(l)} δ(l)
- 计算每一层的偏导数,并更新参数

自动梯度计算
神经网络的参数主要通过梯度下降来优化,需要手动用链式求导来计算风险函数对每个参数的梯度,并转换为计算机程序。
- 手动计算并转换为计算机程序的过程容易出错
目前,主流的深度学习框架都包含了自动梯度计算功能,只需要考虑网络结构并用代码实现,大大提高了开发效率
数值微分
用数值方法计算函数 f ( x ) f(x) f(x) 的导数
f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x f'(x)=\lim\limits_{\Delta x\rightarrow 0}\frac{f(x+\Delta x)-f(x)}{\Delta x} f′(x)=Δx→0limΔxf(x+Δx)−f(x)
-
找到一个合适的 Δ x \Delta x Δx 十分困难
- Δ x \Delta x Δx 过小,会引起数值计算问题,舍入误差
- Δ x \Delta x Δx 过大,会增加截断误差(受模型影响的理论值与数值解之间的误差)
在实际应用中,经常使用以下公式计算梯度,减少截断误差
f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x + Δ x ) 2 Δ x f'(x)=\lim\limits_{\Delta x\rightarrow 0} \frac{f(x+\Delta x)-f(x+\Delta x)}{2\Delta x} f′(x)=Δx→0lim2Δxf(x+Δx)−f(x+Δx) -
数值微分另一个问题是计算复杂度
假设参数数量为 N N N ,则每个参数都需要单独施加扰动,并计算梯度。假设每次正向传播的计算复杂度为 O ( N ) O(N) O(N) ,则计算数值微分的总体时间复杂度为 O ( N 2 ) O(N^2) O(N2)
符号微分
符号计算一般来讲是对输入的表达式,用计算机来通过迭代或递归使用一些事先定义的规则进行转换.当转换结果不能再继续使用变换规则时,便停止计算.
- 一般包括对数学表达式的化简、因式分解、微分、积分、解代数方程、求解常微分方程等运算
符号微分可以在编译时就计算梯度的数学表示,并进一步利用符号计算方法进行优化
且符号计算与平台无关,可在CPU或GPU上运行
缺点:
- 编译时间较长,特别是对于循环,需要很长时间进行编译
- 为了进行符号微分,一般需要设计一种专门的语言来表示数学表达式,并且要对变量(符号)进行预先声明
- 很难对程序进行调试
自动微分
符号微分:处理数学表达式
自动微分:处理一个函数或一段程序
基本原理:所欲偶的数值计算可以分解为一些基本操作,包含+, −, ×, / 和一些初等函数exp, log, sin, cos 等,然后利用链式法则来自动计算一个复合函数的梯度
以 f ( x ; w , b ) = 1 e x p ( − ( w x + b ) ) + 1 f(x;w,b)=\frac{1}{exp(-(wx+b))+1} f(x;w,b)=exp(−(wx+b))+11 为例,其中 x x x 为输入标量, w , b w,b w,b 为权重和偏置
计算图
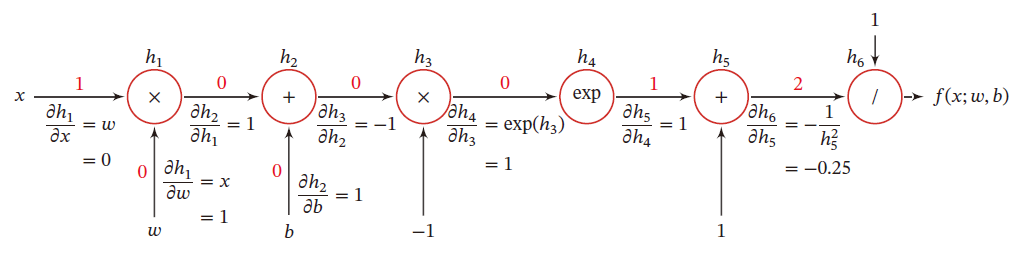

复合函数关于参数的导数可以通过计算图路径上节点的所有导数连乘法得到
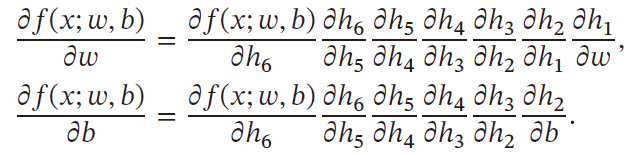
如果函数与参数之间有多条路径,则将这些路径上的导数相加,可以得到最终的梯度
根据计算导数的顺序,自动微分可以分为:前向模式和反向模式
-
前向模式:按照计算图中与参数计算方向相同的方向来递归计算梯度
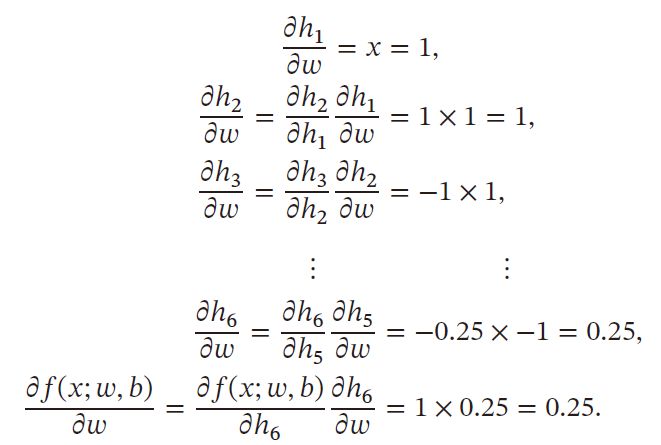
-
反向模式:按照计算图中与参数计算方向相反的方向来计算梯度
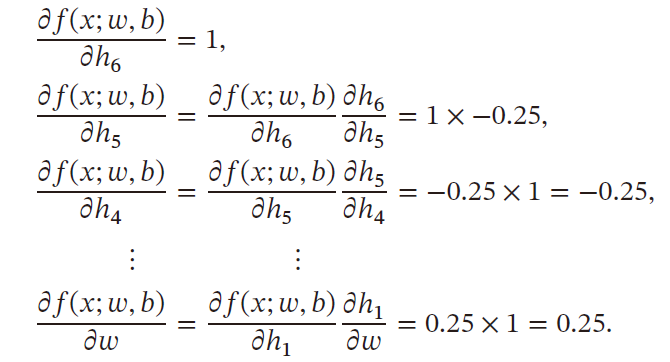
反向模式与反向传播的梯度计算方式相同
准则:
当输入变量的数量大于输出变量的数量,用反向模式
-
前向模式需要对每一个输入都进行遍历
-
反向模式需要对每一个输出都进行遍历
在前馈神经网络中,风险函数为 f : R N → R f:\R^{N}\rightarrow \R f:RN→R 输出为标量,采用反向模式,内存占用小,只需要计算一遍
静态计算图和动态计算图
静态计算图:在编译时构建计算图,运行过程中不可修改
- 在构建时可以进行优化,并行能力强
- 灵活性差
动态计算图:在程序运行时构建计算图
- 不容易优化,输入不同结构的网络,难以并行计算
- 灵活性高
自动微分与符号微分区别
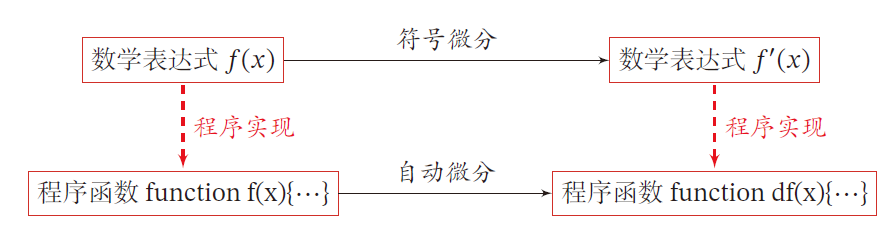
符号微分和自动微分都用计算图和链式法则自动求导
符号微分:
- 符号微分在编译阶段先构造一个符合函数的计算图,通过符号计算得到导数表达式,并对表达式进行优化
- 在程序运行运行阶段才代入变量数值计算导数
自动微分:
- 无需事先编译,程序运行阶段,边计算边记录计算图
- 计算图上的局部梯度都直接代入数值进行计算,然后用前向或反向模式计算最终梯度
优化问题
神经网络的参数学习比线性模型更加困难
- 非凸优化问题
- 梯度消失问题
非凸优化问题
神经网络的优化问题是一个非凸优化问题
y = σ ( w 2 σ ( w 1 x ) ) y=\sigma(w_2\sigma(w_1x)) y=σ(w2σ(w1x))
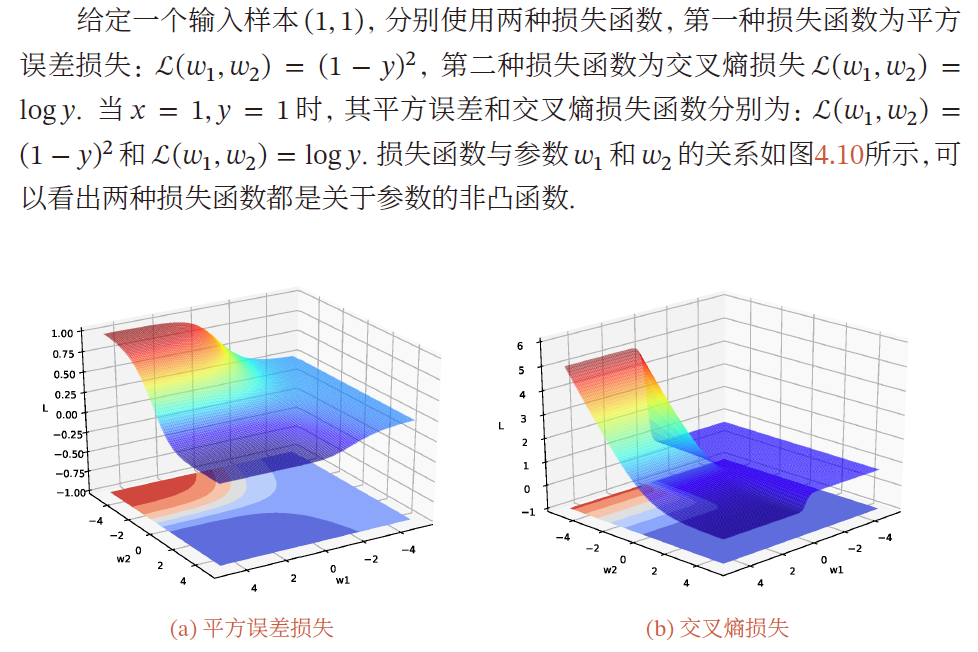
梯度消失问题
在神经网络中,误差反向传播的迭代公式为
δ ( l ) = f l ′ ( z ( l ) ) ⊙ [ ( W ( l + 1 ) ) T δ ( l + 1 ) ] \delta^{(l)}=f'_l(z^{(l)})\odot \left[\left(W^{(l+1)}\right)^T\delta^{(l+1)}\right] δ(l)=fl′(z(l))⊙[(W(l+1))Tδ(l+1)]
误差在反向传播时,在每一层都要乘以该层激活函数的导数
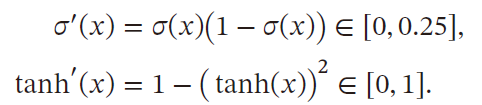
S S S 型激活函数的导数值域都 ≤ 1 \le 1 ≤1
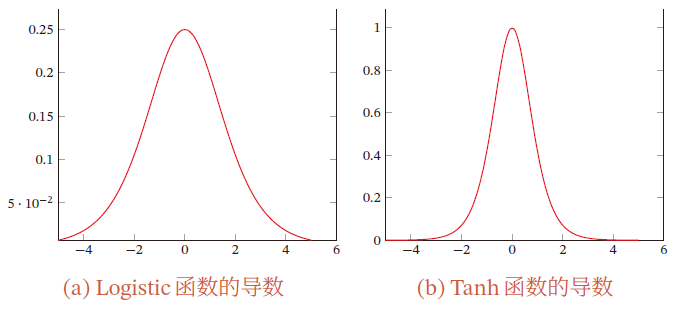
在饱和区导数接近于0,这样误差经过每一层传递会不断衰减,当网络层数很深时,梯度就会不断衰减, 甚至消失,这就是梯度消失问题
- 可以采用导数比较大的激活函数,ReLU函数
1.1.5 全连接的前馈神经网络问题
参数太多
应用于图像处理领域,如果输入图像的像素为 100 × 100 × 3 100\times 100\times 3 100×100×3 ,在全连接网络中,第一层隐藏层的每个神经元到输入层都有 100 × 100 × 3 = 30000 100\times 100\times3=30000 100×100×3=30000 个互相独立的连接,相应的有 30000 30000 30000 个权重参数,随着隐藏层的神经元数量增多,参数的规模也会急剧增加
局部不变性
自然图像中的问题有局部不变形,比如尺寸缩放、平移、旋转等操作不影响语义特征,但全连接的前馈神经网络很难提取这些局部不变的特征——数据增强
相关文章:

【AI】深度学习——前馈神经网络——全连接前馈神经网络
文章目录 1.1 全连接前馈神经网络1.1.1 符号说明超参数参数活性值 1.1.2 信息传播公式通用近似定理 1.1.3 神经网络与机器学习结合二分类问题多分类问题 1.1.4 参数学习矩阵求导链式法则更为高效的参数学习反向传播算法目标计算 ∂ z ( l ) ∂ w i j ( l ) \frac{\partial z^{…...
超简单的视频截取方法,迅速提取所需片段!
“视频可以截取吗?用相机拍摄了一段视频,但是中途相机发生了故障,录进去了很多不需要的片段,现在想截取一部分视频出来,但是不知道方法,想问问广大的网友,知不知道视频截取的方法。” 无论是工…...
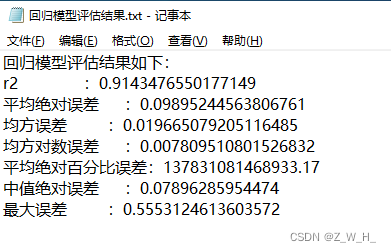
ArcGIS/GeoScene脚本:基于粒子群优化的支持向量机回归模型
参数输入 1.样本数据必须包含需要回归的字段 2.回归字段是数值类型 3.影响因子是栅格数据,可添加多个 4.随机种子可以确保每次运行的训练集和测试集一致 5.训练集占比为0-1之间的小数 6.迭代次数:迭代次数越高精度越高,但是运行时间越长…...

vue3组件的通信方式
一、vue3组件通信方式 通信仓库地址:vue3_communication: 当前仓库为贾成豪老师使用组件通信案例 不管是vue2还是vue3,组件通信方式很重要,不管是项目还是面试都是经常用到的知识点。 比如:vue2组件通信方式 props:可以实现父子组件、子父组件、甚至兄弟组件通信 自定义事件:可…...

Qt QPair
QPair 文章目录 QPair 摘要QPairQPair 特点代码示例QPair 与 QMap 区别 关键字: Qt、 QPair、 QMap、 键值、 容器 摘要 今天在观摩小伙伴撸代码的时候,突然听到了QPair自己使用Qt开发这么就,竟然都不知道,所以趁没有被人发…...
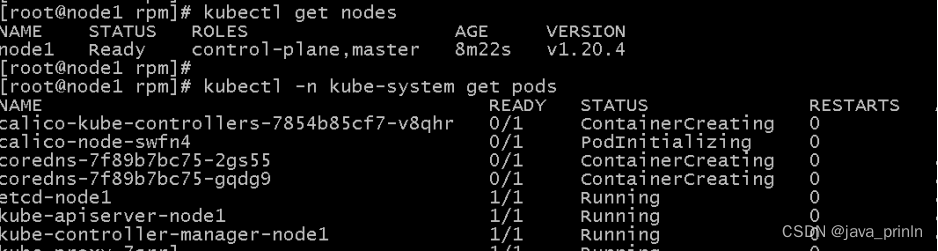
K8S云计算系列-(3)
K8S Kubeadm案例实战 Kubeadm 是一个K8S部署工具,它提供了kubeadm init 以及 kubeadm join 这两个命令来快速创建kubernetes集群。 Kubeadm 通过执行必要的操作来启动和运行一个最小可用的集群。它故意被设计为只关心启动集群,而不是之前的节点准备工作…...

ardupilot罗盘数据计算航向
目录 文章目录 目录摘要1.数据特点2.数据结论1.结论2.结论摘要 本节主要记录ardupilot 根据罗盘数据计算航向的过程。 如果知道了一组罗盘数据,我们可以粗略估计航向:主要后面我们所说的X和Y都是表示的飞机里面的坐标系,也就是X前Y右边,如果按照罗盘坐标系Y实际在左边。 我…...
)
第六章:最新版零基础学习 PYTHON 教程—Python 正则表达式(第一节 - Python 正则表达式)
在本教程中,您将了解RegEx并了解各种正则表达式。 常用表达为什么使用正则表达式基本正则表达式更多正则表达式编译的正则表达式 目录 元字符 为什么是正则表达式?...

docker安装Jenkins完整教程
1.docker拉取 Jenkins镜像并启动容器 新版本的Jenkins依赖于JDK11 我们选择docker中jdk11版本的镜像 # 拉取镜像 docker pull jenkins/jenkins:2.346.3-2-lts-jdk11 2.宿主机上创建文件夹 # 创建Jenkins目录文件夹 mkdir -p /data/jenkins_home # 设置权限 chmod 777 -R /dat…...

[CISCN 2019初赛]Love Math - RCE(异或绕过)
[CISCN 2019初赛]Love Math 1 解题流程1.1 分析1.2 解题题目代码: <?php //听说你很喜欢数学,不知道你是否爱它胜过爱flag if(!isset($_GET[c]))...
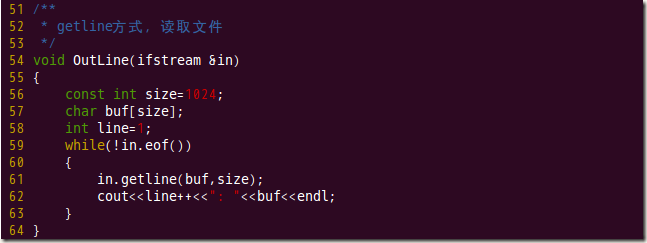
C++ 使用getline()从文件中读取一行字符串
我们知道,getline() 方法定义在 istream 类中,而 fstream 和 ifstream 类继承自 istream 类,因此 fstream 和 ifstream 的类对象可以调用 getline() 成员方法。 当文件流对象调用 getline() 方法时,该方法的功能就变成了从指定文件中读取一行字符串。 该方法有以下 2 种语…...
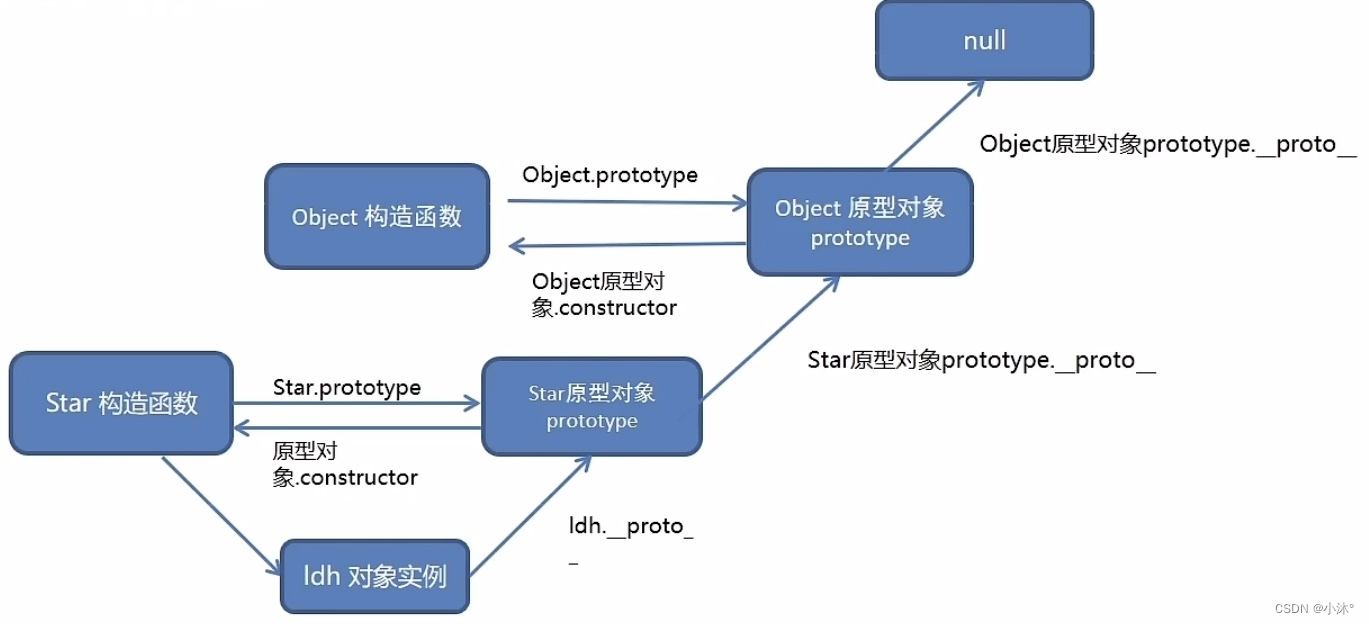
JS进阶-原型
原型 原型就是一个对象,也称为原型对象 构造函数通过原型分配的函数是所有对象所共享的 JavaScript规定,每一个构造函数都有一个prototype属性,指向另一个对象,所以我们也称为原型对象 这个对象可以挂载函数,对象实…...

虹科方案 | 汽车CAN/LIN总线数据采集解决方案
全文导读:现代汽车配备了复杂的电子系统,CAN和LIN总线已成为这些系统之间实现通信的标准协议,为了开发和优化汽车的电子功能,汽车制造商和工程师需要可靠的数据采集解决方案。基于PCAN和PLIN设备,虹科提供了一种高效、…...

HTML5+CSSDAY4综合案例一--热词
样式展示图: 代码如下: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>热词…...
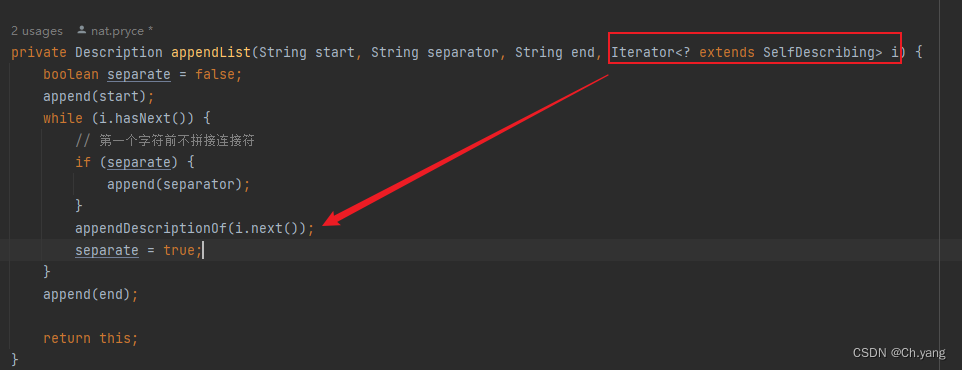
【源码】hamcrest 源码阅读 泛型 extends 和迭代器模式
文章目录 前言1. 泛型参数和自定义迭代器1.1 使用场景1.2 实现 2. 值得一提 前言 官方文档 Hamcrest Tutorial 上篇文章 Hamcrest 源码阅读及空对象模式、模板方法模式的应用 本篇文章 迭代器模式 1. 泛型参数和自定义迭代器 hamcrest 作为一个matcher库,把某个…...
IntelliJ IDEA 2023.1 版本可以安装了
Maven 的导入时间更加快了。 收到的有邮件提醒安装。 安装后的版本,其实就是升级下,并没有什么主要改变。 IntelliJ IDEA 2023.1 版本可以安装了 - 软件技术 - OSSEZMaven 的导入时间更加快了。 收到的有邮件提醒安装。 安装后的版本,其实就是…...

安全论坛和外包平台汇总
文章目录 一. 网络安全论坛汇总二. 外包平台汇总1. 国内:2. 国外 一. 网络安全论坛汇总 安全焦点BugTraq:http://www.fuzzysecurity.com/Exploit-DB:https://www.exploit-db.com/hackone:https://www.hackerone.com/FreeBuf&…...

9-2-Dataset创建-import调用
文章目录 utils_dataset.pymain-调用utils_dateset.pyutils_dataset.py 1默认:没有改变尺寸,数据集中的图像可以是任意形状尺寸。dataloader中必须令batch_size=1 transforms.Resize((宽,高))(image) 和 batch_size=1 必须用其一 原因:当batch_size>1时,每个batch的数…...

XSS原理
原理: 这是一种将任意 Javascript 代码插入到其他Web用户页面里执行以达到攻击目的的漏洞。攻击者利用浏览器的动态展示数据功能,在HTML页面里嵌入恶意代码。当用户浏览改页时,这些潜入在HTML中的恶意代码会被执行,用户浏览器被攻…...
)
记一个带批注、表头样式的导入导出excel方法(基于easyexcel)
技术栈:easyexcel-2.2.10,poi-4.1.2,lombok,hutool-5.8.19;公司自用导入导出方法,可能不是那么的优雅,但胜在稳定实用。 /*** Author 955* Date 2023-10-10 11:52* Description 错误批注信息对…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...