D. Triangle Coloring【组合数学,乘法逆元】
链接
分析
题目要求我们去求出最优的染色的方法数。首先什么时候是最优的,这里只有两种颜色,不可能取到三条边,即蓝色为B,红色为R,有BBB,RRR,BBR,RRB四种组合,显然最多的就是取两条边,我们想取到所有的最大的两条该如何求组合呢,我们将染色分成2R1B,和2B1R,两者数目相同各占一半就可以了,对于所有的三角形,我们的两种染色方法的分配总共有如下方法.
(n3n6)(\begin{matrix}\frac {n}{3}\\ \frac {n}{6}\end{matrix})(3n6n)
但是仅仅是这样还是不够的,对于这样的分配方案中,每个具体的三角形的内的染色方案还没有确定,例如如果是等边三角形,那么就可以有三种染色方案,可以保留任意两条边,根据乘法原理,对于每一种上面的三角形2R1B或者2B1R的分配方案,我们三角形内部的具体的排列方案有,我们把内部可以取的方案数记作ci,ci可以取1,2,3,看最小的边有几条
∏i=1n3ci\prod_{i=1}^{\frac{n}{3}}c_i∏i=13nci
故最终的方法数是
(n3n6)∏i=1n3ci(\begin{matrix}\frac {n}{3}\\ \frac {n}{6}\end{matrix})\prod_{i=1}^{\frac{n}{3}}c_i(3n6n)∏i=13nci
理论基础
1、乘法逆元:
众所周知,乘法逆元有三种计算方法,扩展欧几里得,费马小定理,还有递推求解。其中费马小定理最简单。对于正整数a,和质数b
ab−1modb≡1a^{b-1}mod~b\equiv 1ab−1mod b≡1
这个定理在a,b互质的时候成立,b如果是素数的时候必然成立,由于我们是在乘积运算中得到的,而且所有的运算均mod b所以a必然不可能b,所以是一定成立的。
a⋅ab−2modb≡1a·a^{b-2}mod~b\equiv 1a⋅ab−2mod b≡1
可以知晓,a^b-2是a的在模b的
利用快速幂可以得到逆元,时间复杂度是O(logb)int范围30次左右
ll po(ll rad, ll idx) {ll res = 1;while (idx) {if (idx & 1) res *= id, res %= p;rad *= rad, rad %= p;idx >>= 1; }return res;
}
ll inv(ll x) {return po(x, p - 2);
}
实现
#include <bits/stdc++.h>
#define ll long long
#define ls (p << 1)
#define rs (p << 1 | 1)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair<int, int> PII;
const int N = 2e5 + 5, p = 998244353;
int vis[N];
ll po(ll rad, ll idx) {ll res = 1;while (idx) {if (idx & 1) res *= rad, res %= p;rad *= rad, rad %= p;idx >>= 1; }return res;
}
ll inv(ll x) {return po(x, p - 2);
}
void solve() {int n;cin >> n;ll x = 1, y = 1;for (int i = n / 3; i >= n / 3 - n / 6 + 1; i--) {x *= i, x %= p;//从n一直乘到n-m+1 y *= n / 3 + 1 - i, y %= p;//从1一直乘到m } ll c = x * inv(y) % p;//组合数ll ans = 1;for (int i = 0; i < n / 3; i++) {int a[3];cin >> a[0] >> a[1] >> a[2];sort(a, a + 3);ll cnt = 0;for (int j = 0; j < 3; j++) {if (a[j] == a[0]) cnt++;}ans *= cnt, ans %= p;} cout << ans * c % p << '\n';
}
int main(){ios::sync_with_stdio(false);cin.tie(0);int T = 1;
// cin >> T;while (T--) solve();return 0;
}相关文章:

D. Triangle Coloring【组合数学,乘法逆元】
链接 分析 题目要求我们去求出最优的染色的方法数。首先什么时候是最优的,这里只有两种颜色,不可能取到三条边,即蓝色为B,红色为R,有BBB,RRR,BBR,RRB四种组合,显然最多的就是取两条边,我们想取到…...
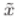
【读论文】AttentionFGAN
【读论文】AttentionFGAN介绍网络架构提取红外图像目标信息的网络辨别器损失函数生成器损失函数辨别器损失函数总结参考论文: https://ieeexplore.ieee.org/document/9103116/如有侵权请联系博主介绍 好久没有读过使用GAN来实现图像融合的论文了,正好看…...

ClickHouse 配置文件使用说明
本文主要介绍 ClickHouse 的配置文件。在 ClickHouse 中配置主要分为两类,一类是负责 server 端配置的,另一类是负责用户端配置的。负责 server 端配置的一般会放在 config.xml 文件中,负责用户端配置的一般会放在 users.xml 文件中。当然如果…...

如果不是互联网人,谁会找到这些神器?
一、上线啦 你肯定该问了,这个是什么鬼东西。它本来是一个创建自己网站的网站。 现在使用它可以创建自己的小程序,又不是有点小厉害了。 而且功能强大,还支持微信支付,分销,优惠券,营销等多种功能。 还有多…...

Neo4j优化
使用参数 查询参数 :params设置参数 :param actorName: Tom Hanks参数的冒号后要用空格使用参数用 $ MATCH (p:Person)-[:ACTED_IN]->(m:Movie) WHERE p.name $actorName RETURN m.released AS releaseDate,m.title AS title ORDER BY m.released DESC多个参数 MATCH (p:Pe…...

CF1692G 2^Sort 题解
CF1692G 2^Sort 题解题目链接字面描述题面翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思路代码实现题目 链接 https://www.luogu.com.cn/problem/CF1692G 字面描述 题面翻译 给你一个长度为 n(∑n<2⋅105)n \ (\sum n < 2\cdot 10^5)n (∑n<…...

关于物理像素,逻辑像素,像素比
关于物理像素、逻辑像素(css像素)、分辨率、像素比的超详细讲解 在日常生活中,有这样一个问题。同样的图片为什么在不同的设备上显示的大小是不一样的。🤒带着这个问题来说明一下。 一、物理像素 设备刚生产出来就已经固定了&a…...

JavaSE基础部分总结
JavaSe基础部分 文章目录JavaSe基础部分1.命名规范2.基本的数据类型3.方法3.1方法的基本格式3.2 方法的分类3.3 方法的注释4.数组4.1 数组的命名格式4.2 数组中存在的址交换的操作4.3数组Arrays常用的方法1. Arrays.asList(数组作为参数或者数据作为参数):2.Arrays.…...

C++基础知识
目录类和对象C static_cast、dynamic_cast、const_cast和reinterpret_cast1、为什么要引入这四种类型转化?2、应用场景。C/C类型转换的本质struct和class的区别为什么会诞生面向对象的编程思想析构函数的执行时机初始化 const 成员变量C const对象(常对象…...
2023/2/24 图数据库Neo4j的理解与应用
1 什么是图数据库(graph database) 十大应用案例:https://go.neo4j.com/rs/710-RRC-335/images/Neo4j-Top-Use-Cases-ZH.pdf “大数据”每年都在增长,但如今的企业领导者不仅需要管理更大规模的数据,还迫切需要从现有…...

适合视力障碍者的Linux
导读有哪些最适合视障用户的 Linux 发行版?让我们一起来看看。 如果有人视力障碍或失明,他们可能会依赖声音提示或其他交互方式(如盲文)来阅读和交流。 他们怎样才能使用 Linux 发行版? 嗯,一般来说&…...

Tina Linux 存储开发指南
Tina Linux 存储开发指南 1 概述 1.1 编写目的 介绍TinaLinux Flash,分区,文件系统等存储相关信息,指导方案的开发定制。 1.2 适用范围 Tina V3.0 及其后续版本。 1.3 相关人员 适用于TinaLinux 平台的客户及相关技术人员。 2 分区管…...
)
【洛谷 P2670】[NOIP2015 普及组] 扫雷游戏 题解(模拟)
[NOIP2015 普及组] 扫雷游戏 题目背景 NOIP2015 普及组 T2 题目描述 扫雷游戏是一款十分经典的单机小游戏。在 nnn 行 mmm 列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。玩家翻…...
【nohup引发磁盘读写高】nohup命令导致服务器磁盘读写占满该如何修复?
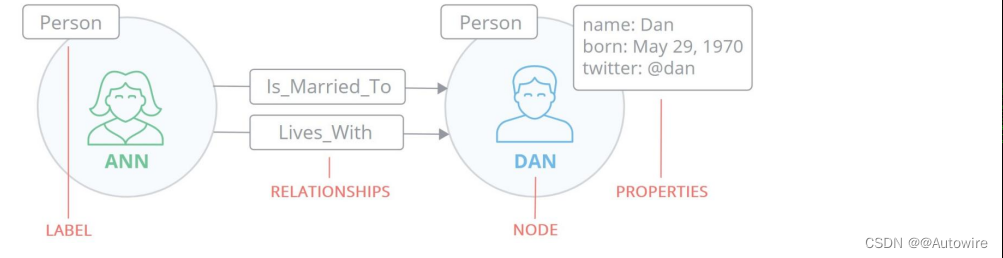
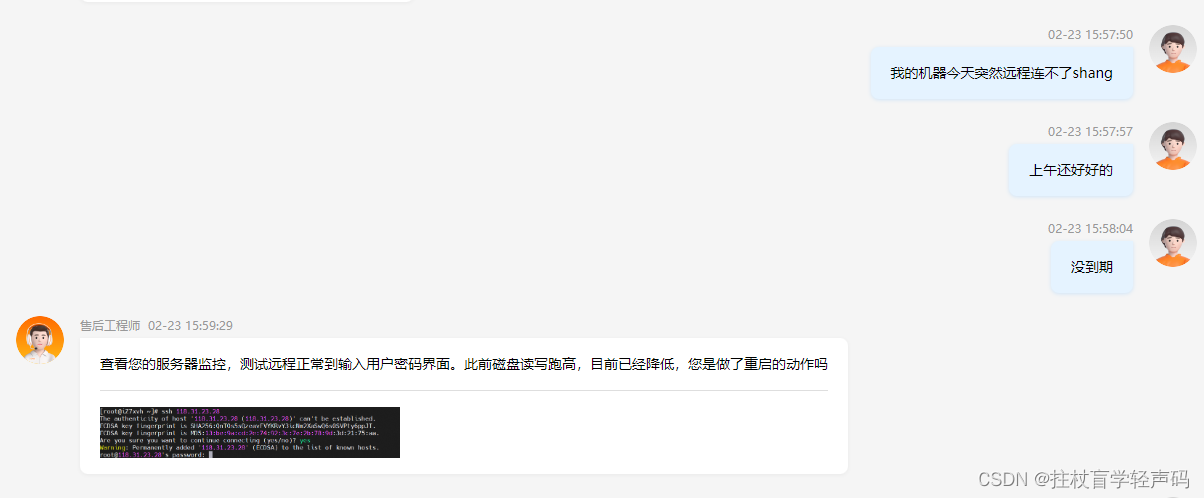
【写在前面】自己在跑一个项目的时候,猛然发现服务器挂了,直接访问不了,呈现出一种卡死现象,我当时都懵了,难道阿里在后端升级,也不会选择在工作日的时间升级吧,于是乎就咨询了一下客服。才有下…...

MySQL(二)索引和SQL优化
MySQL进阶MySQL体系结构存储引擎存储引擎特点InnoDB逻辑存储结构MyISAMMemory存储引擎选择索引索引结构二叉树B-TreeBTreeHash索引分类索引语法SQL性能分析工具SQL执行频率慢查询日志profile详情explain索引使用联合索引索引失效情况SQL提示覆盖索引前缀索引单列索引与联合索引…...
Java常用日期类(包含三代)_Date类及Calendar类等
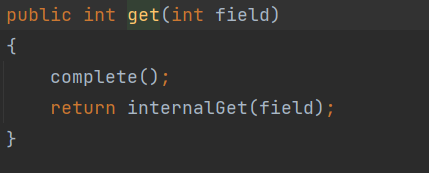
一.java.util.Date类概述从JDK 1.0出现。表示一个日期和时间,精确到毫秒,内部getTime()从1970年1月1号开始算。1. java.util.Date类构造部份构造已经过时,重点看以下两个构造。public Date()从运行程序的此时此刻到时间原点经历的毫秒值&…...

计算机网络你都懂了吗
文章目录一、计算机网络的定义简单定义通用定义二、计算机网络通信过程三、什么是网络协议(Protocol)四、网络协议组成及功能一、计算机网络的定义 简单定义 计算机网络是一些相互连接的、自治的计算机系统的集合。 通用定义 将处于不同位置并具有独…...

3.4 Spring Boot 日志配置
第3章 Spring Boot 的系统配置 3.1 Spring Boot 系统配置文件 3.2 Spring Boot 自定义配置项 3.3 Spring Boot 其他配置 3.4 Spring Boot 日志配置 3.5 实战:Spring Boot 实现系统多环境配置 3.4 Spring Boot 日志配置 日志对于系统监控、故障定位非常重要…...
3款百里挑一的国产软件,逆天好用,装了就舍不得卸载
推荐3款让你偷懒,让你上头的提效电脑软件,个个功能强大,让你远离加班! 很多几个小时才能做好的事情,用上它们,只需要5分钟就行!! 1、JNPF快速开发平台 JNPF 是一款精巧耐用的软件…...
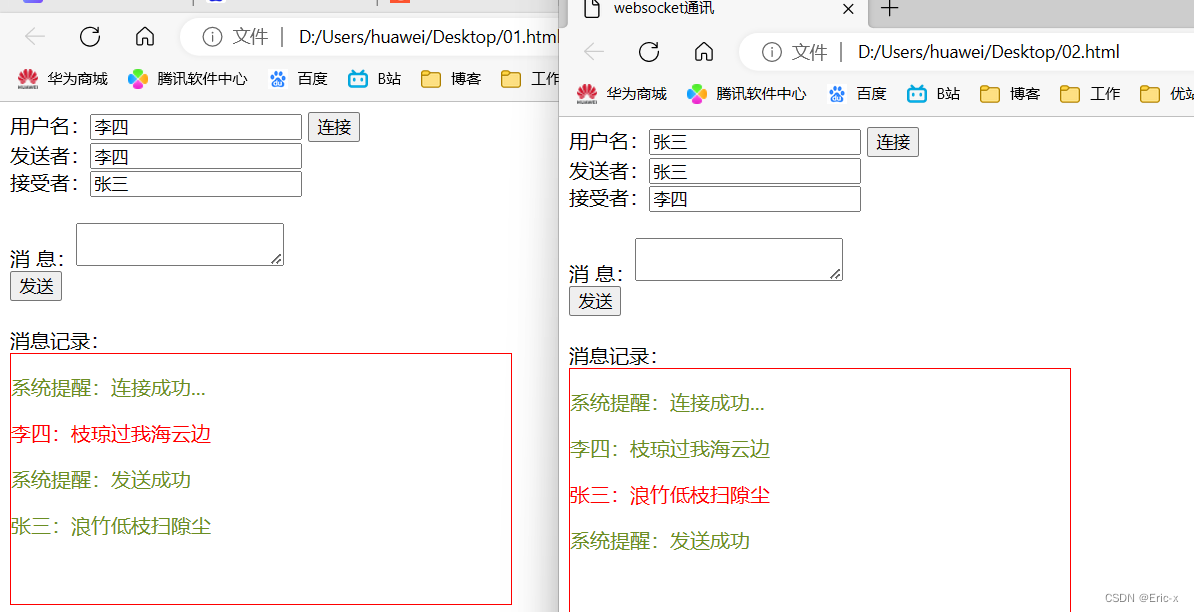
Java实现在线沟通功能
文章目录1、介绍 和 特点2、整合SpringBoot2.1、导入依赖2.2、websocket 配置类2.3、消息处理类2.4、启动服务2.5、前端代码:张三2.6、前端代码:李四3、效果4、小结1、介绍 和 特点 t-io是基于JVM的网络编程框架,和netty属同类,所…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
