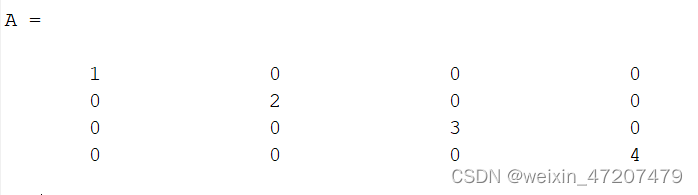线性代数中涉及到的matlab命令-第二章:矩阵及其运算
目录
1,矩阵定义
2,矩阵的运算
3,方阵的行列式和伴随矩阵
4,矩阵的逆
5,克莱默法则
6,矩阵分块
1,矩阵定义
矩阵与行列式的区别:
(1)形式上行列式是数表加两个竖线,矩阵是数表加大括号或中括号;
(2)行列式可计算得到一个值,矩阵不能;
(3)两个行列式相加与两个矩阵相加不同;
(4)行列式乘以一个数k,可将k乘到行列式任一行或任一列,矩阵乘以k,k与矩阵的每个元素相乘;
(5)行列式是n*n的数表,矩阵可以是m*n的数表;
行数和列数都为n的矩阵称为n阶矩阵,或叫n阶方阵;
只有一行的矩阵称为行矩阵(也叫行向量)在Matlab中的表示方法:

只有一列的矩阵称为列矩阵(也叫列向量)在Matlab中的表示方法:

两个矩阵A、B的行数相同,并且列数也相同时,称它们是同型矩阵,如果他们的对应元素也相同,则A = B;
使用size命令获得矩阵的行数和列数:
clc;A = [2 4 6;3 5 7];size(A)使用isequal判断两个矩阵是否相等:
clc;A = [2 4 6;3 5 7];B = [2 4 6;3 5 7];isequal(A,B)单位矩阵:是一个方阵,主队角元素都为1,其他元素是0,一般用E表示

矩阵A乘以单位矩阵E结果还是矩阵A,并且左乘或右乘单位矩阵E一样:
clc;A = [1 2 3;4 5 6;7 8 9];E = eye(3); EA = E*AAE = A*E对角矩阵:是一个方阵,主对角元素不为0,其他元素均为0;
clc;v = [1,2,3,4];A = diag(v)2,矩阵的运算
矩阵的加法:
clc;A = [1 1 1 1;2 2 2 2;3 3 3 3];B = [0 0 0 0;1 1 1 1;2 2 2 2];C = A + B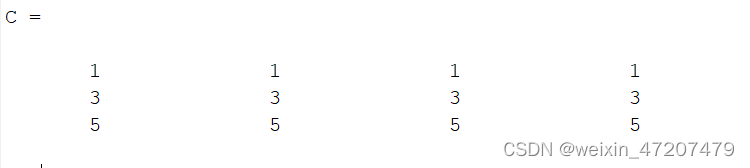 数与矩阵相乘:
数与矩阵相乘:

clc;A = [1 1 1 1;2 2 2 2;3 3 3 3];k = 2;C = k*A
 矩阵相乘:一个矩阵的列与另一个矩阵的行相同时,两个矩阵才能相乘;
矩阵相乘:一个矩阵的列与另一个矩阵的行相同时,两个矩阵才能相乘;
clc;A = [1 1 1;2 2 2];B = [1 1;2 2;3 3];C = A*BD = B*A 
可见矩阵A*B 不等于B*A;

矩阵的幂:

以下例子为四个城市之间开通的航线情况,0代表两个城市间没有航线,1代表开通有航线,建立城市间是否有航线的模型即一个4阶矩阵A,用![]() 表示从i城市到j城市的航线数量,对A求2次幂可以得到城市i有几条双向航线(A的2次幂矩阵的对角线元素),以及从城市i经过一次中转到城市j的单线航线数量。
表示从i城市到j城市的航线数量,对A求2次幂可以得到城市i有几条双向航线(A的2次幂矩阵的对角线元素),以及从城市i经过一次中转到城市j的单线航线数量。

对角矩阵的幂,对角线上元素按幂运算:
clc;v = [1,2,3];A = diag(v)A^3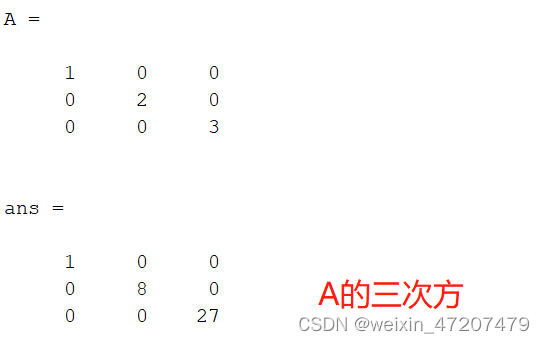
矩阵的转置:

clc;A = [1 1 1;2 2 2];B = A'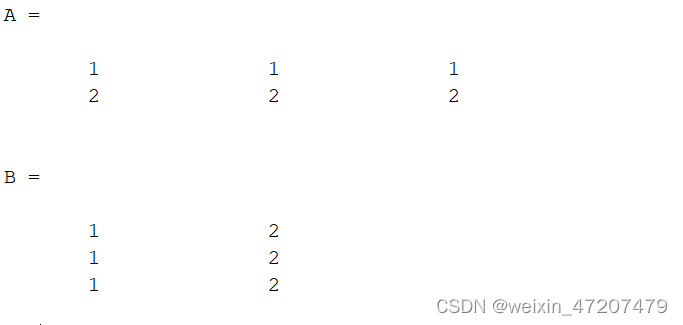
 一个方阵和它的转置矩阵相加可以产生一个对称矩阵,以下程序可以产生一个对称阵:
一个方阵和它的转置矩阵相加可以产生一个对称矩阵,以下程序可以产生一个对称阵:
clc;A = rand(3);B = A';C= A+B 
3,方阵的行列式和伴随矩阵

clc;A = rand(3);a = det(A);b = det(A');abs(a-b) < epsclc;A = rand(3);B = rand(3);format shorta = det(A*B);
b = det(A)*det(B);abs(a-b) < epsclc;A = [1 2 3;4 5 6;7 8 9];k = 2;B = k*A;det(B) == (k^3)*det(A) 
clc;A = [1 4 7;3 5 8;2 6 8];A_adj = adjoint(A) %adjoint求A的伴随矩阵C = A*A_adj;
D = A_adj*A;
E = eye(3);
EA = E*det(A);A13 = A;A21 = A;A13(1,:) = [];A13(:,3) = [];A21(2,:) = [];A21(:,1) = [];D_A13 = (-1)^(1+3)*det(A13) %A(1,3)的代数余子式D_A21 = (-1)^(2+1)*det(A21) %A(2,1)的代数余子式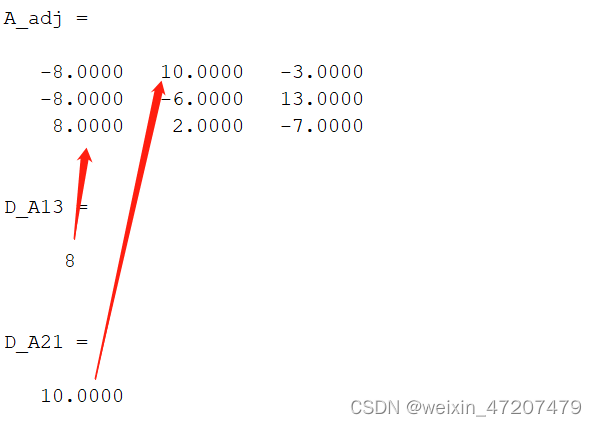
使用Matlab中的adjoint命令,A产生的伴随阵A_adj,A*A_adj = A_adj *A = E*det(A):

4,矩阵的逆

只有方阵才有逆矩阵,矩阵可逆的充分必要条件是det(A)不等于0。
Matlab中可以使用inv(A)或A^(-1)计算A的逆矩阵,也可以使用上图中定理2计算逆矩阵:
clc;A = rand(3);B = inv(A)C = A^(-1);A_mul_B = A*BB_mul_A = B*A;A_adj = adjoint(A);1/det(A)*A_adj %根据定理2计算逆矩阵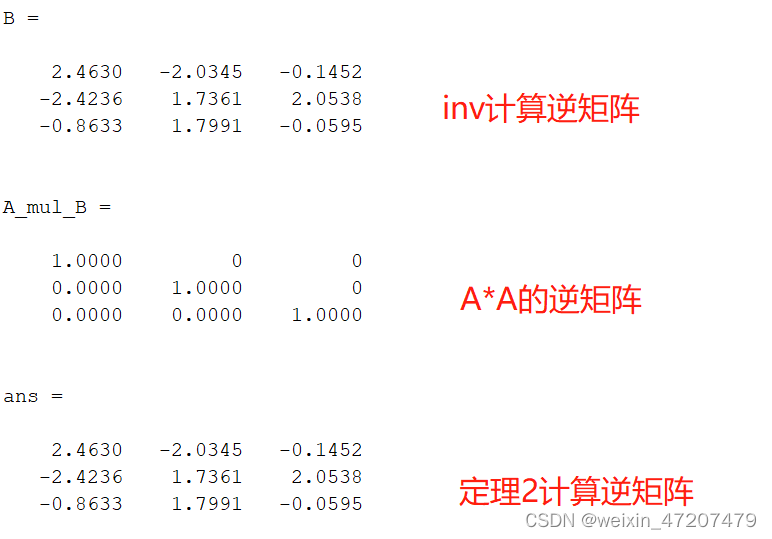 同样使用定理2可以反向计算矩阵A的伴随阵:
同样使用定理2可以反向计算矩阵A的伴随阵:
clc;A = rand(3);A_adj = adjoint(A)det(A)*inv(A) %定理2计算伴随阵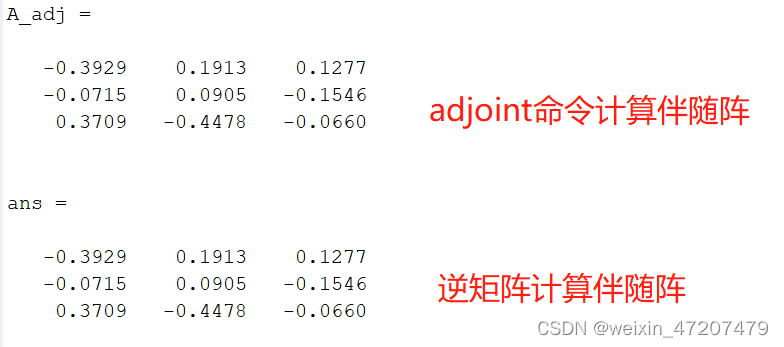

5,克莱默法则

分别用逆矩阵、左除、克莱默法则计算下边例题,计算结果相同:

clc;%以下程序用于求n元非齐次方程组的解, 方程组的形式为Ax = b,求xA = [1,1,1,1;1,2,-1,4;2,-3,-1,-5;3,1,2,11]; %方程组系数矩阵b = [5;-2;-2;0]; %方程组右端常数矩阵A1 = A;
A1(:,1) = b; A2 = A;
A2(:,2) = b;A3 = A;
A3(:,3) = b;A4 = A;
A4(:,4) = b;if det(A) ~= 0 %判断方程组是否有解%%三种求方程组解的形式x = inv(A)*b %1,用逆矩阵的方式求方程组的解x = A\b %2,用左除的方式求方程组的解x1 = det(A1)/det(A) %3,用克莱默法则求方程组的解x2 = det(A2)/det(A)x3 = det(A3)/det(A)x4 = det(A4)/det(A)elsedisp("det(A) = 0,方程组无解");
end6,矩阵分块

使用下边Matlab命令运算得到逆矩阵:
clc;A = [3 0 0 ;0 2 4 ;0 3 1 ];C = mat2cell(A,[1,2],[1,2]); %mat2cell函数将原矩阵分块为四个cell,行数分别为1和2行,列数分别为1列和2列C1 = C{1}; %将cell转化为矩阵
C2 = C{2};
C3 = C{3};
C4 = C{4};inv_A = inv(A) %使用inv命令直接计算逆矩阵inv_C1 = inv(C1); %对分块后的非0矩阵求逆矩阵
inv_C4 = inv(C4);inv_C = [inv_C1,C3;C2,inv_C4] %对原矩阵分块后对非0矩阵分别求逆矩阵后再组合在一起运行结果:

矩阵分块后转置:
clc;A = randi([0,10],3,4) %产生一个3行4列从0-10的随机数元素的矩阵A_T = A'C = mat2cell(A,[1,2],[2,2]); %mat2cell函数将原矩阵分块为四个cell,行数分别为1和2行,列数分别为2列和2列C1 = C{1,1}; %将cell转化为矩阵
C2 = C{1,2};
C3 = C{2,1};
C4 = C{2,2};C1 = C1';
C2 = C2';
C3 = C3';
C4 = C4';C_T = [C1,C3;C2,C4]运行结果:

相关文章:

线性代数中涉及到的matlab命令-第二章:矩阵及其运算
目录 1,矩阵定义 2,矩阵的运算 3,方阵的行列式和伴随矩阵 4,矩阵的逆 5,克莱默法则 6,矩阵分块 1,矩阵定义 矩阵与行列式的区别: (1)形式上行列式…...

计算机毕业设计选什么题目好?springboot 美食推荐系统
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...
爆肝整理,Jmeter接口性能测试-跨线程调用变量实操(超详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、Jmeter中线程运…...
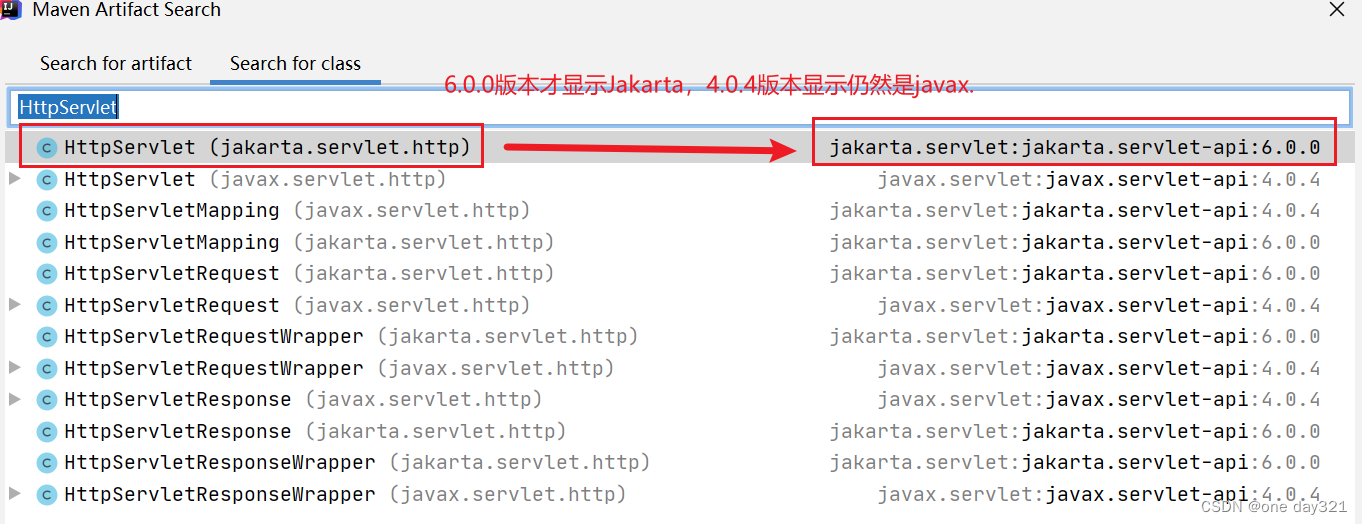
Maven导入程序包jakarta.servlet,但显示不存在
使用前提:(Tomcat10版本)已知tomcat10版本之后,使用jakart.servlet。而tomcat9以及之前使用javax.servlet。 问题描述:在maven仓库有导入了Jakarta程序包,但是界面仍然显示是javax。(下图&…...
es6(二)——常用es6说明
ES6的系列文章目录 es6(一)——var和let和const的区别 文章目录 ES6的系列文章目录一、变量的结构赋值1.数组的结构赋值2.对象的结构赋值 二、模板字符串三、扩展运算符1.字符串的使用2.数组的使用 四、箭头函数1.普通函数的定义2.箭头函数的定义3.箭头…...
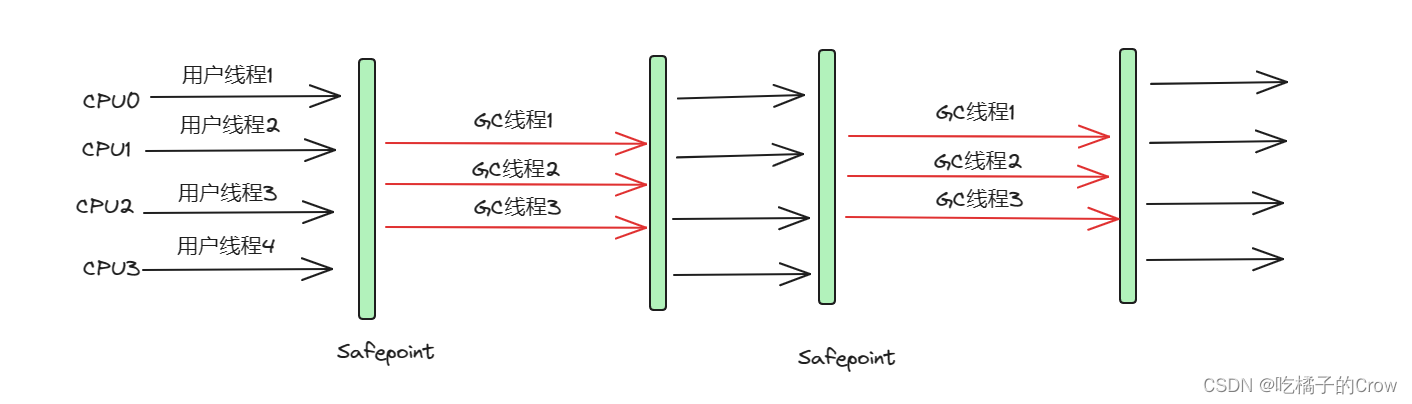
经典垃圾回收器
1.各垃圾回收器之间的配合使用关系 2.垃圾回收器的种类 2.1 Serial收集器(默认新生代收集器) Serial收集器是历史最悠久的收集器,曾经是新生代收集器的唯一选择,它是一个单线程工作的收集器,其“单线程”的意义不仅仅…...

台达DOP-B07S410触摸屏出现HMI no response无法上传的解决办法
台达DOP-B07S410触摸屏出现HMI no response无法上传的解决办法 台达触摸屏(B07S410)在上载程序时(显示No response from HMI)我以前的电脑是WIN7的,从来没出现过这样的问题,现在换成win10的,怎么都不行,(USB显示是一个大容量存储)换一台电脑(win10)有些行,有些不行…...

[资源推荐] 复旦大学张奇老师科研分享
刷B站的时候首页给我推了这个:【直播回放】复旦大学张奇教授亲授:人工智能领域顶会论文的发表指南先前也散漫地读了些许论文,但没有在一些宏观的方法论下去训练,读的时候能感觉出一些科研的套路,论文写作的套路&#x…...

C++数位动态规划算法:统计整数数目
题目 给你两个数字字符串 num1 和 num2 ,以及两个整数 max_sum 和 min_sum 。如果一个整数 x 满足以下条件,我们称它是一个好整数: num1 < x < num2 min_sum < digit_sum(x) < max_sum. 请你返回好整数的数目。答案可能很大&…...

ip 网段设置 --chatGPT
问:host all all 127.0.0.1/32 scram-sha-256 里的 127.0.0.1/32 是什么含义 ,要指定某个呢 gpt: 在 PostgreSQL 的 pg_hba.conf 文件中,127.0.0.1/32 是一个用于定义访问控制规则的CIDR(无类域间路由)标记࿰…...

使用JMeter进行接口测试教程
安装 使用JMeter的前提需要安装JDK,需要JDK1.7以上版本目前在用的是JMeter5.2版本,大家可自行下载解压使用 运行 进入解压路径如E: \apache-jmeter-5.2\bin,双击jmeter.bat启动运行 启动后默认为英文版本,可通过Options – Cho…...

文本生成解码策略
解码策略 1. sample实现了怎样的功能 不是直接选择概率最大的token,而是根据多项式分布进行采样获得下一个token 这里的概率通过设置一些策略,进行处理。例如,解码最小长度(当长度小于该值的时候,eos的采样概率为0&am…...
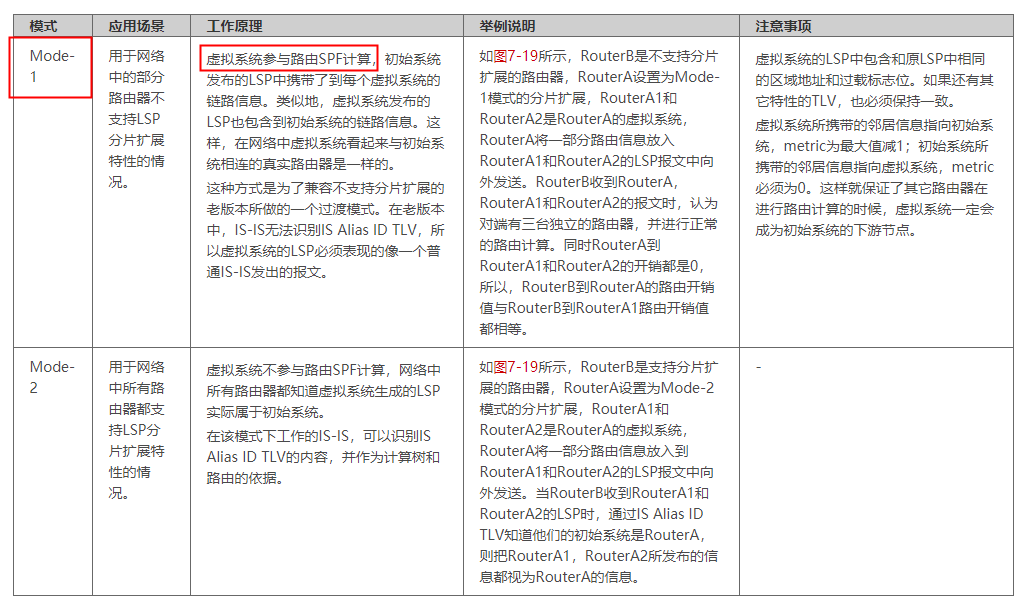
华为数通方向HCIP-DataCom H12-831题库(单选题:221-240)
第221题 以下关于IS-IS的LSP分片功能的描述,正确的是哪一项? A、IS-IS的分片扩展功能的Mode-1模式,虚拟系统是需要参与路由SPF计算的 B、IS-IS的LSP分片功能,是用于让收到LSP分片报文的设备老化相关路由信息 C、IS-IS的分片扩展功能,是通过LSP报文中的LSPID实现的 D、IS-…...

AttributeError: module ‘hanlp.utils.rules‘ has no attribute ‘tokenize_english‘
附原文链接:http://t.csdnimg.cn/wVLib import hanlp tokenizer hanlp.utils.rules.tokenize_english tokenizer(Mr. Hankcs bought hankcs.com for 1.5 thousand dollars.) 改为: from hanlp.utils.lang.en.english_tokenizer import tokenize_eng…...

苍穹外卖(四) AOP切面公共字段自动填充及文件上传
一.AOP切面公共字段填充 问题分析 如果都按照上述的操作方式来处理这些公共字段, 需要在每一个业务方法中进行操作, 编码相对冗余、繁琐,那能不能对于这些公共字段在某个地方统一处理,来简化开发呢? 答案是可以的,我们使用AOP切…...

vue-cli + vue3 项目 ios 苹果手机白屏问题
目录 问题描述原因分析解决方案遇到的坑1,架构问题2,项目引入其他依赖的问题 参考 问题描述 vue-cli vue3 的项目,在苹果手机上打开白屏,安卓手机正常显示。 原因分析 1,借助 vconsole 发现并没有打印报错信息&…...

Spring Boot中的JdbcTemplate是什么,如何使用
Spring Boot中的JdbcTemplate是什么,如何使用 Spring Boot是一个流行的Java应用程序开发框架,它简化了Java应用程序的开发过程,并提供了丰富的功能和工具。在Spring Boot中,JdbcTemplate是一个强大的数据库访问工具,它…...

Python测网络连通性、能否访问某个网络或者端口号<网络检测、ping主机、测试端口>
一、ping命令及其使用 ping命令是在计算机网络领域中用来测试目标主机是否可达以及其延迟时间的命令。对于Python来说,我们可以通过subprocess模块来实现执行命令。下面是示例代码: import subprocessdef ping(host):result subprocess.run([ping, -c…...

【沧元图】玉阳宫主是正是邪,和面具人有勾结吗?现在已有答案了
Hello,小伙伴们,我是小郑继续为大家深度解析沧元图。 沧元图这部动漫中,有一个很特殊的人物,也是一个让人看不透的人物,因为很多人都不知道这个人是正还是邪,这个人就是玉阳宫主。 因为这个人明面上是掌管东宁府维护东…...
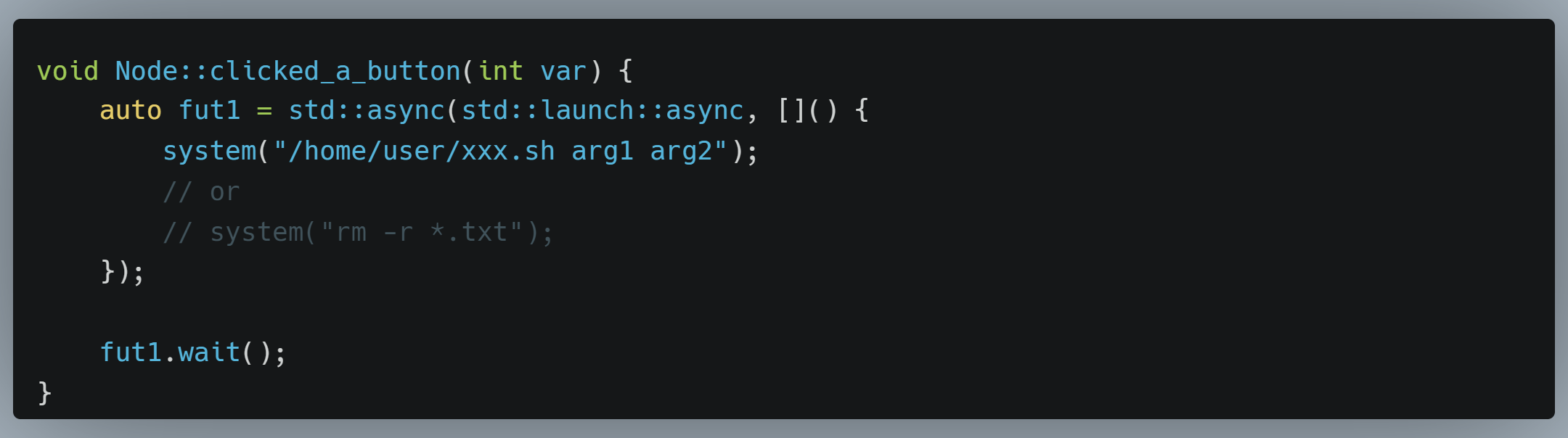
C++笔记之popen()和std_system()和std_async()执行系统命令比较
C笔记之popen()和std_system()和std_async()执行系统命令比较 code review! 文章目录 C笔记之popen()和std_system()和std_async()执行系统命令比较1.popen()2.std::system()3.std::async()——C11提供的异步操作库,适合在多线程中执行外部命令,建议使…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...