electron sha512 checksum mismatch
sha512 checksum mismatch错误
此错误常常发生在electron检查更新时,导致检查更新失败。
自动更新使用的模块
electron-updater
or
electron-differential-updater
win下electron-builder打包
使用electron-builder打包之后,进行版本增量更新遇到的错误提示。
sha512 checksum mismatch
这个问题的出现有以下几种情况:
- 使用较早版本的electron-updater,建议更新electron-updater版本到5.x.x。
- publish里的url指向的地址中,latest.yml忘记更新。
- 打包缓存问题,修改version为更高的值,重新打包。
(经过测试,express,minio文件服务器增量更新无此报错。)
/!\ 注意:如果自己写下载接口,该接口应为支持分片下载的。否则下载数据量将会超出原安装包大小的几十倍,且会造成校验和错误。
相关文章:

electron sha512 checksum mismatch
sha512 checksum mismatch错误 此错误常常发生在electron检查更新时,导致检查更新失败。 自动更新使用的模块 electron-updater or electron-differential-updater win下electron-builder打包 使用electron-builder打包之后,进行版本增量更新遇到的…...
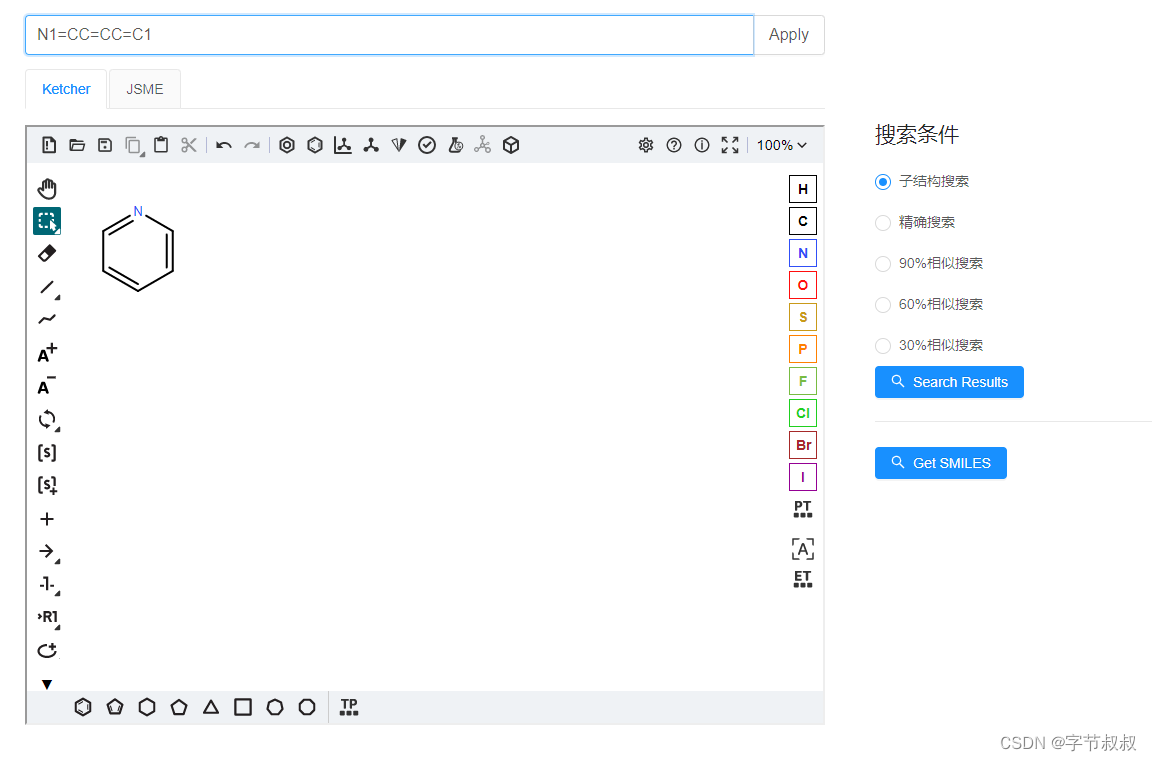
使用Chemistry Development Kit (CDK) 来进行化学SMILES子结构匹配
摘要 SMILES是一种用于描述化合物结构的字符串表示法,其中子结构搜索是在大规模化合物数据库中查找特定的结构。然而,这种搜索方法存在一个误解,即将化合物的子结构视为一个独立的实体进行搜索,而忽略了它们在更大的化合物中的上…...

CMake模块的使用和自定义模块
CMake模块的使用和自定义模块一、前言二、使用Find模块2.1、准备工作2.2、添加头文件路径和库文件2.3、< name >_FOUND 来控制工程特性三、编写自定义的Find模块3.1、 准备工作3.2、cmake 模块3.3、使用自定义的FindHELLO 模块构建工程3.4、如果没有找到hello library四、…...

jvm调优参数配置
在JVM启动参数中,可以设置跟内存、垃圾回收相关的一些参数设置,默认情况不做任何设置JVM会工作的很好,但对一些配置很好的Server和具体的应用必须仔细调优才能获得最佳性能。通过设置我们希望达到一些目标: GC的时间足够的小 GC的…...

Leetcode.1567 乘积为正数的最长子数组长度
题目链接 Leetcode.1567 乘积为正数的最长子数组长度 Rating : 1710 题目描述 给你一个整数数组 nums,请你求出乘积为正数的最长子数组的长度。 一个数组的子数组是由原数组中零个或者更多个连续数字组成的数组。 请你返回乘积为正数的最长子数组长度…...
)
部分库与使用方法总结(自用)
1.tqdm tqdm是Python的进度条库,可以在长循环操作中显示进度提示 tqdm.tqdm:传入数字 from tqdm import tqdm for i in tqdm(range(1, 5)):print(i)使用bar_format "{l_bar}{bar}"可以只显示进度条 from tqdm import tqdm for i in tqdm(range(1, 5), ba…...

C++实现日期类
文章目录前言1.日期类的功能分析1.大致分析2.接口设计2.具体实现1.日期类的成员函数和成员变量2.初始化(构造函数)3.对日期进行天数推算4.比较相关的运算符重载5.前置后置自增或自减6.日期相减与流插入流提取1.日期相减2.重载流插入和流提取3.总结前言 之前介绍了C…...
想成为一名专业黑客,但不知道从哪里学起?我来教你。
成为一名黑客需要学什么? 想成为一名专业黑客,但不知道从哪里学起”很多人在后台问过这个问题,今天就为你介绍成为专业黑客必须学习的十个方面的知识,希望能为迷惘中的你指明方向。 想要成为网络hacker黑客?先来学习…...

VMware ESXi 7.0 U3k Unlocker OEM BIOS 集成网卡驱动和 NVMe 驱动 (集成驱动版)
ESXi 7 U3 标准版集成 Intel 网卡、USB 网卡 和 NVMe 驱动 请访问原文链接:https://sysin.org/blog/vmware-esxi-7-u3-sysin/,查看最新版。原创作品,转载请保留出处。 作者主页:www.sysin.org 本次针对 2023-02-21 发布的 ESXi …...

新的计算方法:预测益生菌在不同生长条件下的相互作用
谷禾健康 益生菌可以产生有益的维生素、消化酶、必需氨基酸、免疫调节和抗菌代谢产物,从而促进人体健康,预防肠道炎症性疾病、自身免疫性疾病和胃肠道感染。其宝贵特性已得到健康行业、医疗专业人士和公众的认可。 比起单菌株益生菌,多菌株益…...

python自学之《21天学通Python》(13)——第16章 数据库编程
数据库指的是以一定方式存储在一起、能为多个用户共享、具有尽可能小的冗余度、与应用程序彼此独立的数据集合。而我们平时所说的数据库实际上是包含了数据库管理系统(DBMS)的,数据库管理系统是为管理数据库而设计的软件系统,它一…...

[架构之路-118]-《软考-系统架构设计师》-软架构设计-11-可靠性相关设计
第11节 可靠性相关设计11.1 可靠性基本概念可靠性工程是研究产品生命周期中故障的发生、发展规律,达到预防故障,消灭故障,提高产品可用性的工程技术。信息系统的可靠性是指系统在满足一定条件的应用环境中能够正常工作的能力,可以…...
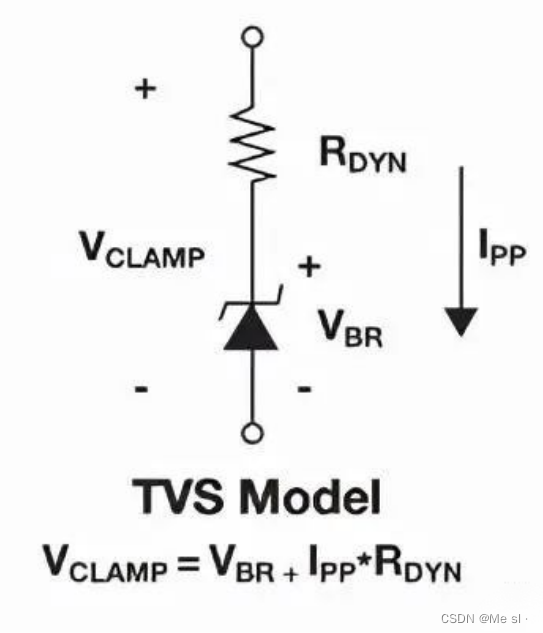
电阻串联的作用
电阻串联常见作用 第一个作用是:阻抗匹配: 因为信号源的阻抗很低,跟信号线之间阻抗不匹配,串上一个电阻后,可以改善匹配情况,以减少反射,避免振荡等。 常见的阻抗匹配方法 1、使用变压器来做…...

leetcode 1675. Minimize Deviation in Array(最小化数组偏差)
数组里面有n个正整数,里面的数字可以无限次进行如下操作: 1.偶数可以除以2 2.奇数可以乘以2 数组中任意两元素差的最大值称为偏差。 把数组中的元素进行上面2种操作,使偏差最小。 思路: 数组中现有2种数字,一种是奇数…...

特征向量中心度(eigenvector centrality)算法原理与源码解析
前言 随着图谱应用的普及,图深度学习技术也逐渐被越来越多的数据挖掘团队所青睐。传统机器学习主要是对独立同分布个体的统计学习,而图深度学习则是在此基础上扩展到了非欧式空间的图数据之上,通过借鉴NLP和CV方向的模型思想,衍生…...
Vue3 中组件的使用(上)
目录前言:一、什么是组件二、注册组件1. 全局注册2. 局部注册二、传递数据【父 -> 子】1. 字符串数组的形式2. 对象的形式三、组件事件【子 -> 父】1. 字符串数组式声明自定义事件2. 【子组件】触发组件事件3. 【父组件】监听子组件自定义事件4. 组件事件例子…...
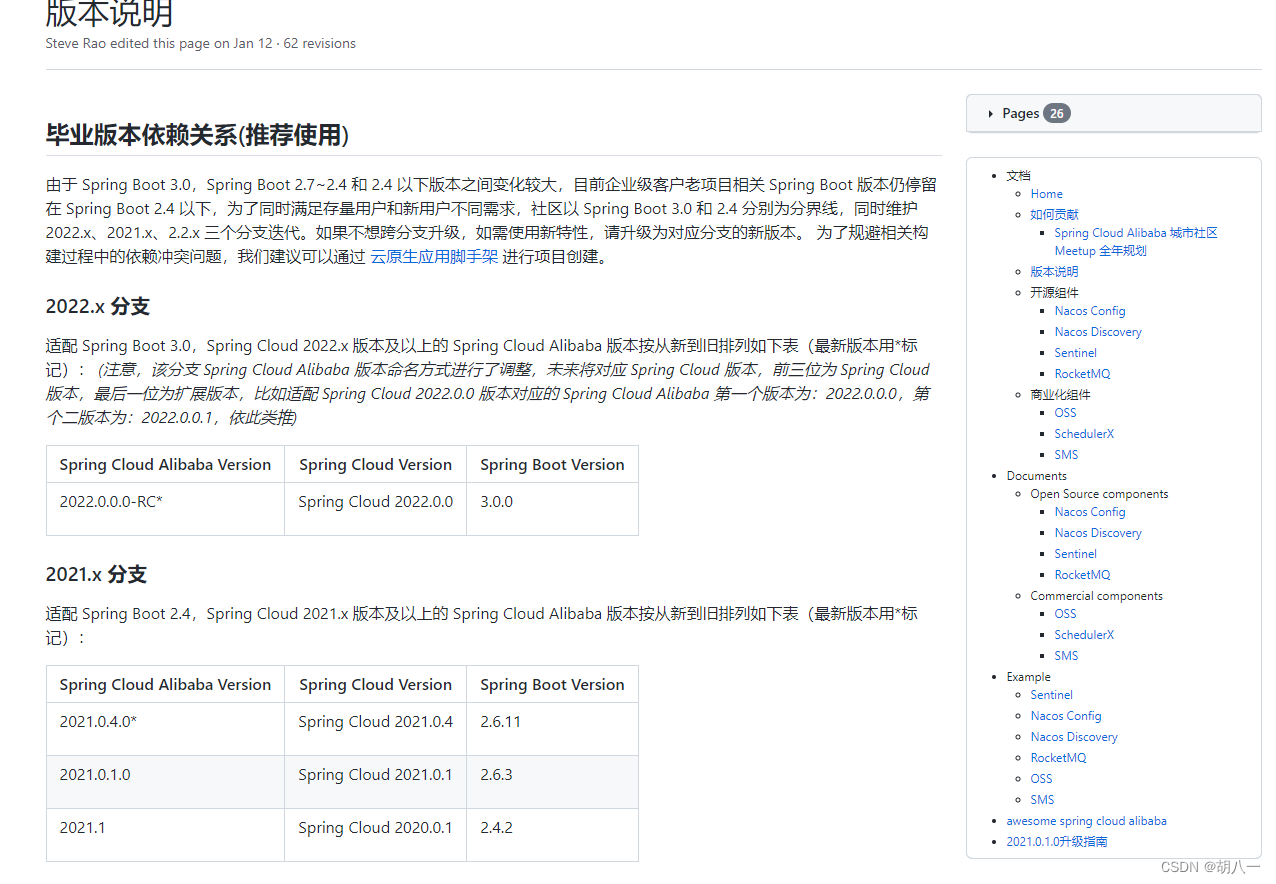
spring-boot、spring-cloud、spring-cloud-alibaba版本对应
一、查询 spring-boot(spring-boot-starter-parent) 版本号 https://mvnrepository.com/artifact/org.springframework.boot/spring-boot-starter-parent 二、查询 spring-cloud(spring-cloud-dependencies) 版本号 https://mvnrepository.com/artifact/org.springframework…...
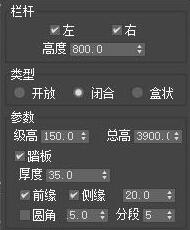
【沐风老师】3DMAX一键楼梯脚本插件StairGenerator使用教程
3DMAX一键楼梯插件StairGenerator,不需要花费太多的时间,轻松从2D平面图生成3D楼梯模型,生成的楼梯模型细节丰富真实。 【主要功能】 1.简单:轻松实现2D到3D建模。 2.具有最详细三维结构的台阶平面图。 3.楼梯各部件完全参数化…...
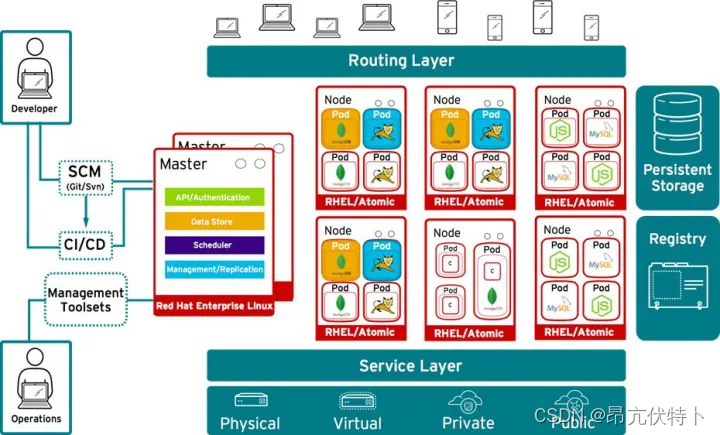
OpenShift 简介
OpenShift 是红帽 Red Hat 公司基于开源的云平台,是平台即服务(PaaS),是一种容器应用平台。允许开发人员构建、测试和部署云应用。该系统是在 K8S 核心之上添加工具,从而实现更快的应用开发、部署及扩展。 在 OpenShi…...

netty自定义封包实现
文章目录说明分享内置编码器和解码器解码器编码器代码实现创建核心类消息实体类自定义编码类自定义解码类服务端ServerHandler入口类客户端ClientHandler入口类测试参考总结说明 netty是java重要的企业级NIO,使用它可以快速实现很多功能通信功能如:http、…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...

使用ch340继电器完成随机断电测试
前言 如图所示是市面上常见的OTA压测继电器,通过ch340串口模块完成对继电器的分路控制,这里我编写了一个脚本方便对4路继电器的控制,可以设置开启时间,关闭时间,复位等功能 软件界面 在设备管理器查看串口号后&…...
